Шестиугольная призма - Википедия - Hexagonal prism
| Униформа шестиугольная призма | |
|---|---|
 | |
| Тип | Призматический однородный многогранник |
| Элементы | F = 8, E = 18, V = 12 (χ = 2) |
| Лица по сторонам | 6{4}+2{6} |
| Символ Шлефли | t {2,6} или {6} × {} |
| Символ Wythoff | 2 6 | 2 2 2 3 | |
| Диаграммы Кокстера | |
| Симметрия | D6ч, [6,2], (* 622), порядок 24 |
| Группа вращения | D6, [6,2]+, (622), заказ 12 |
| Рекомендации | U76 (г) |
| Двойной | Гексагональная дипирамида |
| Характеристики | выпуклый, зоноэдр |
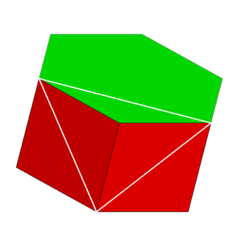 Фигура вершины 4.4.6 | |

В геометрия, то шестиугольная призма это призма с шестиугольник основание. Этот многогранник имеет 8 граней, 18 ребер и 12 вершин.[1]
Поскольку в нем 8 лица, это октаэдр. Однако срок октаэдр в основном используется для обозначения правильный октаэдр, имеющий восемь треугольных граней. Из-за неоднозначности термина октаэдр и сходство различных восьмиугольников, этот термин редко используется без пояснения.
Перед заточкой многие карандаши принять форму длинной шестиугольной призмы.[2]
Как полуправильный (или равномерный) многогранник
Если все грани правильные, шестиугольная призма - это полуправильный многогранник в более общем плане равномерный многогранник, а четвертый - в бесконечном наборе призм, образованных квадратными сторонами и двумя правильными многоугольниками. Это можно рассматривать как усеченный шестиугольный осоэдр, представлена Символ Шлефли т {2,6}. В качестве альтернативы его можно рассматривать как Декартово произведение правильного шестиугольника и отрезок, и представлен произведением {6} × {}. В двойной шестиугольной призмы - это шестиугольная бипирамида.
В группа симметрии правой шестиугольной призмы D6ч порядка 24. группа ротации является D6 порядка 12.
Объем
Как и в большинстве призм, объем определяется по площади основания с длиной стороны , и умножив его на высоту , давая формулу:[3]
Симметрия
Топология однородной шестиугольной призмы может иметь геометрические вариации более низкой симметрии, в том числе:
| Имя | Правильно-шестиугольная призма | Шестиугольная усеченная | Дитригональная призма | Триамбическая призма | Дитригональная трапеция |
|---|---|---|---|---|---|
| Симметрия | D6ч, [2,6], (*622) | C6v, [6], (*66) | D3ч, [2,3], (*322) | D3D, [2+,6], (2*3) | |
| Строительство | {6}×{}, | т {3} × {}, | s2{2,6}, | ||
| Изображение |  |  | 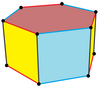 |  | |
| Искажение | 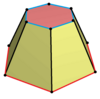 |  |   |  | |
Как часть пространственной мозаики
Он существует в виде ячеек четырех призматических однородные выпуклые соты в 3-х измерениях:
| Гексагональные призматические соты[1] | Треугольно-шестиугольные призматические соты | Плоские треугольные-шестиугольные призматические соты | Ромбитреугольно-шестиугольные призматические соты |
 | 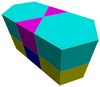 |  | 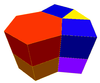 |
Он также существует в виде ячеек ряда четырехмерных равномерные 4-многогранники, включая:
Связанные многогранники и мозаики
| Однородные шестиугольные двугранные сферические многогранники | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |  |  |  |  |  |  | ||||||||
| {6,2} | т {6,2} | г {6,2} | т {2,6} | {2,6} | rr {6,2} | tr {6,2} | sr {6,2} | с {2,6} | ||||||
| Двойники к униформе | ||||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
Этот многогранник можно рассматривать как член последовательности однородных узоров с фигурой вершины (4.6.2p) и Диаграмма Кокстера-Дынкина ![]()
![]()
![]()
![]()
![]() . За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры ), показанные ниже в виде сферических мозаик. За п > 6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.
. За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры ), показанные ниже в виде сферических мозаик. За п > 6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.
| *п32 мутации симметрии полностью усеченных мозаик: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п32 [п,3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | [3i, 3] | |
| Цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |  |  |  |  |  |  |  |  |  |  |  |
| Конфиг. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Смотрите также
| Семья униформы призмы | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Многогранник | |||||||||||
| Coxeter | |||||||||||
| Плитка | |||||||||||
| Конфиг. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 |
Рекомендации
- ^ а б Пью, Энтони (1976), Многогранники: визуальный подход, University of California Press, стр. 21, 27, 62, ISBN 9780520030565.
- ^ Симпсон, Одри (2011), Базовая математика для Кембриджского IGCSE, Cambridge University Press, стр. 266–267, ISBN 9780521727921.
- ^ Уитер, Кэролайн С. (2007), Геометрия, Career Press, стр. 236–237, ISBN 9781564149367.
внешняя ссылка
- Равномерные соты в 3-м пространстве Модели VRML
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников Призмы и антипризмы
- Вайсштейн, Эрик В. «Гексагональная призма». MathWorld.
- Интерактивная модель с гексагональной призмой - работает в вашем браузере
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |