Равномерная черепица - Википедия - Uniform tiling
В геометрия, а равномерная черепица это мозаика самолета правильный многоугольник сталкивается с ограничением бытия вершинно-транзитивный.
Однородные мозаики могут существовать как в Евклидова плоскость и гиперболическая плоскость. Равномерные мозаики связаны с конечным равномерные многогранники которые можно рассматривать как равномерные мозаики сфера.
Наиболее однородные мозаики можно сделать из Строительство Wythoff начиная с группа симметрии и особая образующая точка внутри фундаментальная область. Плоская группа симметрии имеет многоугольную фундаментальная область и может быть представлен именем группы, представленным порядком зеркал в последовательных вершинах.
Треугольник фундаментальной области равен (п q р) и прямоугольный треугольник (п q 2), где п, q, р целые числа больше 1. Треугольник может существовать как сферический треугольник, плоский евклидов треугольник или гиперболический плоский треугольник, в зависимости от значений п, q и р.
Существует ряд символических схем для наименования этих фигур из модифицированного Символ Шлефли для областей прямоугольного треугольника: (п q 2) → {п, q}. В Диаграмма Кокстера-Дынкина - треугольный граф с п, q, р маркированы по краям. Если р = 2, граф является линейным, поскольку узлы области порядка 2 не генерируют отражений. В Символ Wythoff берет 3 целых числа и разделяет их вертикальной чертой (|). Если точка генератора находится вне зеркала напротив узла домена, она указывается перед полосой.
Наконец, мозаики можно описать их конфигурация вершины, последовательность многоугольников вокруг каждой вершины.
Все равномерные мозаики можно построить из различных операций, применяемых к правильные мозаики. Эти операции, названные Норман Джонсон называются усечение (вырезание вершин), исправление (обрезка вершин до исчезновения ребер) и песня (режущие кромки). Омнитуркация это операция, сочетающая усечение и наклонение. Стаббинг - это операция альтернативное усечение полностью усеченной формы. (Видеть Равномерный многогранник # операторы построения Wythoff Больше подробностей.)
Группы Кокстера
Группы Кокстера для плоскости определяют конструкцию Wythoff и могут быть представлены как Диаграммы Кокстера-Дынкина:
Для групп с целыми номерами заказов, в том числе:
| Орбифолд симметрия | Группа Кокстера | Coxeter диаграмма | Примечания | ||
|---|---|---|---|---|---|
| Компактный | |||||
| *333 | (3 3 3) | [3[3]] | 3 светоотражающие формы, 1 курносый | ||
| *442 | (4 4 2) | [4,4] | 5 светоотражающих форм, 1 курносый | ||
| *632 | (6 3 2) | [6,3] | 7 светоотражающих форм, 1 курносый | ||
| *2222 | (∞ 2 ∞ 2) | × | [∞,2,∞] | 3 светоотражающие формы, 1 курносый | |
| Некомпактный (фриз ) | |||||
| *∞∞ | (∞) | [∞] | |||
| *22∞ | (2 2 ∞) | × | [∞,2] | 2 светоотражающие формы, 1 курносый | |
| Орбифолд симметрия | Группа Кокстера | Coxeter диаграмма | Примечания | |
|---|---|---|---|---|
| Компактный | ||||
| * pq2 | (p q 2) | [p, q] | 2 (p + q) | |
| * pqr | (p q r) | [(p, q, r)] | pq + pr + qr | |
| Паракомпакт | ||||
| * ∞p2 | (p ∞ 2) | [p, ∞] | р> = 3 | |
| * ∞pq | (p q ∞) | [(p, q, ∞)] | р, д> = 3, р + д> 6 | |
| * ∞∞p | (р ∞ ∞) | [(p, ∞, ∞)] | р> = 3 | |
| *∞∞∞ | (∞ ∞ ∞) | [(∞,∞,∞)] | ||
Равномерные мозаики евклидовой плоскости
На евклидовой плоскости есть группы симметрии, построенные из фундаментальных треугольников: (4 4 2), (6 3 2) и (3 3 3). Каждый представлен набором линий отражения, которые делят плоскость на фундаментальные треугольники.
Эти группы симметрии создают 3 правильные мозаики, и 7 полурегулярных. Некоторые полуправильные мозаики повторяются из разных конструкторов симметрии.
Призматическая группа симметрии, представленная (2 2 2 2), представляет собой два набора параллельных зеркал, которые, как правило, могут иметь прямоугольную фундаментальную область. Он не создает новых мозаик.
Еще одна призматическая группа симметрии, представленная (∞ 2 2), которая имеет бесконечную фундаментальную область. Он строит две однородные мозаики: апейрогональная призма и апейрогональная антипризма.
Укладка конечных граней этих двух призматических мозаик образует одну не уайтоффианец равномерная мозаика плоскости. Это называется удлиненная треугольная черепица, состоящий из чередующихся слоев квадратов и треугольников.
Фундаментальные треугольники под прямым углом: (п q 2)
| (п q 2) | Фонд. треугольники | Родитель | Усеченный | Исправленный | Bitruncated | Двунаправленный (двойной) | Собранный | Усеченный (Усеченный) | Курносый |
|---|---|---|---|---|---|---|---|---|---|
| Символ Wythoff | q | п 2 | 2 q | п | 2 | п q | 2 п | q | п | q 2 | п q | 2 | п q 2 | | | п q 2 | |
| Символ Шлефли | {п,q} | т{п,q} | г {р, д} | 2t {p, q} = t {q, p} | 2r {p, q} = {q, p} | рр {р, q} | tr {p, q} | sr {p, q} | |
| Диаграмма Кокстера | |||||||||
| Конфигурация вершины. | пq | q.2p.2p | (p.q)2 | п. 2 кв. 2 кв. | qп | п. 4.q.4 | 4.2p.2q | 3.3.стр. 3.q | |
| Квадратная плитка (4 4 2) |  |  {4,4} |  4.8.8 |  4.4.4.4 |  4.8.8 |  {4,4} |  4.4.4.4 |  4.8.8 |  3.3.4.3.4 |
| Шестиугольная черепица (6 3 2) |  |  {6,3} |  3.12.12 |  3.6.3.6 |  6.6.6 |  {3,6} |  3.4.6.4 |  4.6.12 |  3.3.3.3.6 |
Общие фундаментальные треугольники: (p q r)
| Символ Wythoff (p q r) | Фонд. треугольники | q | п р | r q | п | г | p q | r p | q | p | q r | p q | р | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Диаграмма Кокстера | |||||||||
| Конфигурация вершины. | (p.q)р | r.2p.q.2p | (p.r)q | q.2r.p. 2r | (q.r)п | q.2r.p. 2r | r.2q.p. 2кв. | 3.r.3.q.3.p | |
| Треугольная (3 3 3) |  |  (3.3)3 |  3.6.3.6 |  (3.3)3 |  3.6.3.6 |  (3.3)3 |  3.6.3.6 |  6.6.6 |  3.3.3.3.3.3 |
Непростые фундаментальные области
Единственная возможная фундаментальная область в евклидовом 2-пространстве, которая не является симплекс - прямоугольник (∞ 2 ∞ 2), причем Диаграмма Кокстера: ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Все формы, созданные из него, становятся квадратная черепица.
. Все формы, созданные из него, становятся квадратная черепица.
Равномерные мозаики гиперболической плоскости
Равномерных мозаик выпуклых правильных многоугольников на плоскости бесконечно много. гиперболическая плоскость, каждая из которых основана на другой группе отражающей симметрии (p q r).
Выборка показана здесь с Диск Пуанкаре проекция.
В Диаграмма Кокстера-Дынкина дается в линейной форме, хотя на самом деле это треугольник с конечным сегментом r, соединяющимся с первым узлом.
Другие группы симметрии существуют в гиперболической плоскости с четырехугольными фундаментальными областями, начинающимися с (2 2 2 3) и т. Д., Которые могут порождать новые формы. Также существуют фундаментальные области, в которых вершины размещаются на бесконечности, например (∞ 2 3) и т. Д.
Фундаментальные треугольники под прямым углом: (п q 2)
| (p q 2) | Фонд. треугольники | Родитель | Усеченный | Исправленный | Bitruncated | Двунаправленный (двойной) | Собранный | Усеченный (Усеченный) | Курносый |
|---|---|---|---|---|---|---|---|---|---|
| Символ Wythoff | q | п 2 | 2 q | п | 2 | p q | 2 п | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Символ Шлефли | т {р, д} | т {р, д} | г {р, д} | 2t {p, q} = t {q, p} | 2r {p, q} = {q, p} | рр {р, q} | tr {p, q} | sr {p, q} | |
| Диаграмма Кокстера | |||||||||
| Фигура вершины | пq | (q.2p.2p) | (p.q.p.q) | (стр. 2q. 2q) | qп | (стр. 4.q.4) | (4.2p.2q) | (3.3.п. 3.q) | |
| (5 4 2) |  V4.8.10 |  {5,4} |  4.10.10 |  4.5.4.5 |  5.8.8 |  {4,5} |  4.4.5.4 |  4.8.10 |  3.3.4.3.5 |
| (5 5 2) |  V4.10.10 |  {5,5} | 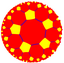 5.10.10 |  5.5.5.5 | 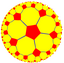 5.10.10 |  {5,5} |  5.4.5.4 |  4.10.10 |  3.3.5.3.5 |
| (7 3 2) |  V4.6.14 |  {7,3} |  3.14.14 |  3.7.3.7 |  7.6.6 |  {3,7} |  3.4.7.4 |  4.6.14 |  3.3.3.3.7 |
| (8 3 2) |  V4.6.16 |  {8,3} |  3.16.16 |  3.8.3.8 |  8.6.6 |  {3,8} |  3.4.8.4 |  4.6.16 |  3.3.3.3.8 |
Общие фундаментальные треугольники (p q r)
| Символ Wythoff (p q r) | Фонд. треугольники | q | п р | r q | п | г | p q | r p | q | p | q r | p q | р | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Диаграмма Кокстера | |||||||||
| Фигура вершины | (p.r)q | (r.2p.q.2p) | (p.q)р | (q.2r.p. 2r) | (q.r)п | (r.2q.p. 2q) | (2р. 2кв. 2р) | (3.r.3.q.3.p) | |
| (4 3 3) | 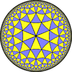 V6.6.8 |  (3.4)3 |  3.8.3.8 |  (3.4)3 |  3.6.4.6 |  (3.3)4 |  3.6.4.6 |  6.6.8 |  3.3.3.3.3.4 |
| (4 4 3) |  V6.8.8 |  (3.4)4 |  3.8.4.8 |  (4.4)3 |  3.6.4.6 |  (3.4)4 |  4.6.4.6 |  6.8.8 |  3.3.3.4.3.4 |
| (4 4 4) |  V8.8.8 |  (4.4)4 |  4.8.4.8 |  (4.4)4 |  4.8.4.8 |  (4.4)4 |  4.8.4.8 |  8.8.8 |  3.4.3.4.3.4 |
Расширенные списки однородных мозаик
Список однородных мозаик можно расширить несколькими способами:
- Фигуры вершин могут иметь ретроградные грани и более одного раза поворачиваться вокруг вершины.
- Звездный многоугольник плитки могут быть включены.
- Апейрогоны, {∞}, можно использовать как грани замощения.
- Ограничение, что плитки пересекаются от края до края, можно ослабить, допуская дополнительные мозаики, такие как Пифагорейская черепица.
Треугольники группы симметрии с ретроградами включают:
- (4/3 4/3 2) (6 3/2 2) (6/5 3 2) (6 6/5 3) (6 6 3/2)
Треугольники группы симметрии с бесконечностью включают:
- (4 4/3 ∞) (3/2 3 ∞) (6 6/5 ∞) (3 3/2 ∞)
Бранко Грюнбаум в книге 1987 г. Плитки и узорыв разделе 12.3 перечисляется список из 25 однородных мозаик, включая 11 выпуклых форм, и добавляются еще 14, которые он называет полые мозаики который включал первые два вышеупомянутых расширения, грани звездообразного многоугольника и фигуры вершин.
H.S.M. Coxeter и др., в статье 1954 г. «Равномерные многогранники», в Таблица 8: Равномерная мозаика, использует первые три разложения и перечисляет в общей сложности 38 однородных мозаик. Если также учитывать мозаику из 2 апейрогонов, то в сумме можно считать 39 однородных мозаик.


Помимо 11 выпуклых решений, 28 однородных звездных мозаик, перечисленных Кокстером и другие., сгруппированные по графам общих ребер, показаны ниже. Для наглядности в первых семи мозаиках апейрогоны не раскрашены, и после этого раскрашены только многоугольники вокруг одной вершины.
| #[1] | Диаграмма | Вершина Конфиг | Wythoff | Симметрия | Примечания |
|---|---|---|---|---|---|
| I1 | ∞.∞ | p1m1 | (Две плитки полуплоскости, апейрогональная мозаика порядка 2 ) | ||
| I2 | 4.4.∞ | ∞ 2 | 2 | p1m1 | Апейрогональная призма | |
| I3 | 3.3.3.∞ | | 2 2 ∞ | p11g | Апейрогональная антипризма |
| Группа обоев симметрия | ||||||
|---|---|---|---|---|---|---|
| Макнил[1] | Грюнбаум[2] | Край диаграмма | Твердый | Вершина Конфиг | Wythoff | Симметрия |
| I4 |  |  | 4.∞.4/3.∞ 4.∞.-4.∞ | 4/3 4 | ∞ | p4m | |
| I5 |  |  | (3.∞.3.∞.3.∞)/2 | 3/2 | 3 ∞ | p6m | |
| I6 |  |  | 6.∞.6/5.∞ 6.∞.-6.∞ | 6/5 6 | ∞ | ||
| I7 |  | ∞.3.∞.3/2 ∞.3.∞.-3 | 3/2 3 | ∞ | |||
| 1 | 15 |  |  | 3/2.12.6.12 -3.12.6.12 | 3/2 6 | 6 | p6m |
| 16 |  | 4.12.4/3.12/11 4.12.4/3.-12 | 2 6 (3/2 6/2) | | |||
| 2 |  |  | 8/3.4.8/3.∞ | 4 ∞ | 4/3 | p4m | |
| 7 |  | 8/3.8.8/5.8/7 8/3.8.-8/3.-8 | 4/3 4 (4/2 ∞/2) | | |||
 | 8.4/3.8.∞ 8.-4.8.∞ | 4/3 ∞ | 4 | ||||
| 3 |  |  | 12/5.6.12/5.∞ | 6 ∞ | 6/5 | p6m | |
| 21 |  | 12/5.12.12/7.12/11 12/5.12.-12/5.-12 | 6/5 6 (6/2 ∞/2) | | |||
 | 12.6/5.12.∞ 12.-6.12.∞ | 6/5 ∞ | 6 | ||||
| 4 | 18 | 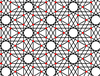 |  | 12/5.3.12/5.6/5 | 3 6 | 6/5 | p6m |
| 19 |  | 12/5.4.12/7.4/3 12/5.4.-12/5.-4 | 2 6/5 (3/2 6/2) | | |||
| 17 |  | 4.3/2.4.6/5 4.-3.4.-6 | 3/2 6 | 2 | |||
| 5 |  |  | 8.8/3.∞ | 4/3 4 ∞ | | p4m | |
| 6 |  |  | 12.12/5.∞ | 6/5 6 ∞ | | p6m | |
| 7 | 6 | 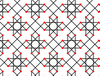 |  | 8.4/3.8/5 4.8.-8/3 | 2 4/3 4 | | p4m |
| 8 | 13 | 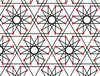 |  | 6.4/3.12/7 -6.4.12/5 | 2 3 6/5 | | p6m |
| 9 | 12 |  |  | 12.6/5.12/7 -12.6.12/5 | 3 6/5 6 | | p6m |
| 10 | 8 | 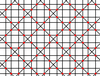 |  | 4.8/5.8/5 -4.8/3.8/3 | 2 4 | 4/3 | p4m |
| 11 | 22 | 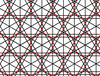 |  | 12/5.12/5.3/2 12/5.12/5.-3 | 2 3 | 6/5 | p6m |
| 12 | 2 |  |  | 4.4.3/2.3/2.3/2 4.4.-3.-3.-3 | не уайтоффианец | см |
| 13 | 4 |  | 4.3/2.4.3/2.3/2 4.-3.4.-3.-3 | | 2 4/3 4/3 | p4g | |
| 14 |  | 3.4.3.4/3.3.∞ 3.4.3.-4.3.∞ | | 4/3 4 ∞ | p4g | ||
Самодвойственные мозаики
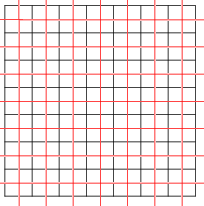
Плитки также могут быть самодвойственный. Квадратная черепица с Символ Шлефли {4,4}, самодвойственный; здесь показаны две квадратные мозаики (красный и черный), двойственные друг другу.
Равномерные мозаики с использованием звездчатых многоугольников

π / 8.4**
π / 4.8*
π / 4 считается не сквозным из-за большого квадрата, хотя его можно интерпретировать как звездообразный многоугольник с парами коллинеарных ребер.
Увидев звездный многоугольник поскольку невыпуклый многоугольник с вдвое большим количеством сторон допускает звездообразные многоугольники, и их учет как правильные многоугольники позволяет использовать их в равномерная черепица. Эти многоугольники помечены как {Nα} для изотоксальный невыпуклый 2N-угольник с внешним двугранным углом α. Его внешние вершины обозначены как N*
α, а внутренний N**
α. Это расширение определения требует, чтобы углы только с двумя полигонами не считались вершинами. Мозаика определяется своим конфигурация вершины как циклическую последовательность выпуклых и невыпуклых многоугольников вокруг каждой вершины. Есть 4 таких однородных мозаики с регулируемыми углами α и 17 одинаковых мозаик, которые работают только с определенными углами.[3]
Все эти мозаики топологически связаны с обычными однородными мозаиками с выпуклыми правильными многоугольниками, при этом 2-валентные вершины игнорируются, а квадратные грани в виде двуугольников сводятся к одному ребру.
 3.6* α.6** α Топологический 3.12.12 |  4.4* α.4** α Топологический 4.8.8 |  6.3* α.3** α Топологический 6.6.6 |  3.3* α.3.3** α Топологический 3.6.3.6 |
 4.6.4* π / 6.6 Топологический 4.4.4.4 |  (8.4* π / 4)2 Топологический 4.4.4.4 | 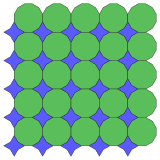 12.12.4* π / 3 Топологический 4.8.8 |  3.3.8* π / 12.4** π / 3.8* π / 12 Топологический 4.8.8 |  3.3.8* π / 12.3.4.3.8* π / 12 Топологический 4.8.8 |  3.4.8.3.8* π / 12 Топологический 4.8.8 |
 5.5.4* 4π / 10.5.4* π / 10 Топологический 3.3.4.3.4 | 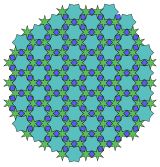 4.6* π / 6.6** π / 2.6* π / 6 Топологический 6.6.6 |  (4.6* π / 6)3 Топологический 6.6.6 |  9.9.6* 4π / 9 Топологический 6.6.6 |  (6.6* π / 3)2 Топологический 3.6.3.6 |  (12.3* π / 6)2 Топологический 3.6.3.6 |
 3.4.6.3.12* π / 6 Топологический 4.6.12 |  3.3.3.12* π / 6.3.3.12* π / 6 Топологический 3.12.12 | 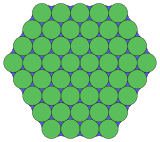 18.18.3* 2π / 9 Топологический 3.12.12 |  3.6.6* π / 3.6 Топологический 3.4.6.4 |  8.3* π / 12.8.6* 5π / 12 Топологический 3.4.6.4 |
Равномерные мозаики с использованием чередующихся многоугольников
Звездные многоугольники вида {pα} также может представлять выпуклые 2п-угольники, чередующиеся под двумя углами, простейший из которых - ромб {2α}. Если разрешить их как правильные многоугольники, мы получим более однородные мозаики, с некоторыми примерами ниже.
 3.2*.6.2** Топологический 3.4.6.4 |  4.4.4.4 Топологический 4.4.4.4 |  (2* π / 6.2** π / 3)2 Топологический 4.4.4.4 |  2* π / 6.2* π / 6.2** π / 3.2** π / 3 Топологический 4.4.4.4 |  4.2* π / 6.4.2** π / 3 Топологический 4.4.4.4 |
Смотрите также
- Символ Wythoff
- Список однородных мозаик
- Равномерные мозаики в гиперболической плоскости
- Равномерный многогранник
Рекомендации
- ^ а б Джим Макнил
- ^ Плитка и узоры, таблица 12.3.1 с.640
- ^ Плитки и узоры Бранко Грюнбаум, Г. Shephard, 1987. 2.5 Плитки с использованием звездных многоугольников, стр.82-85.
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
- Грюнбаум, Бранко; Шепард, Г.С. (1987). Плитки и узоры. В. Х. Фриман и компания. ISBN 0-7167-1193-1. (Звездные плитки, раздел 12.3)
- Х. С. М. Коксетер, М. С. Лонге-Хиггинс, Дж. С. П. Миллер, Равномерные многогранники, Фил. Пер. 1954 г., 246 А, 401–50 JSTOR 91532 (Таблица 8)
внешняя ссылка
- Вайсштейн, Эрик В. «Равномерная тесселяция». MathWorld.
- Равномерные мозаики на плоскости Евклида
- Мозаика на плоскости
- Мир мозаики Дэвида Бейли
- k-однородные мозаики
- n-однородные мозаики
- Клитцинг, Ричард. «4D евклидовы мозаики».
| Космос | Семья | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Равномерная черепица | {3[3]} | δ3 | hδ3 | qδ3 | Шестиугольный |
| E3 | Равномерно выпуклые соты | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Равномерные 4-соты | {3[5]} | δ5 | hδ5 | qδ5 | 24-ячеечные соты |
| E5 | Равномерные 5-соты | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Равномерные 6-соты | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Равномерные 7-соты | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Равномерные 8-соты | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Равномерные 9-соты | {3[10]} | δ10 | hδ10 | qδ10 | |
| Eп-1 | Униформа (п-1)-соты | {3[n]} | δп | hδп | qδп | 1k2 • 2k1 • k21 |












