Четверть гиперкубические соты - Quarter hypercubic honeycomb
В геометрия, то четверть гиперкубических сот (или же четверть n-кубических сот) - бесконечный размерный ряд соты, на основе гиперкубические соты. Дается Символ Шлефли q {4,3 ... 3,4} или символ Кокстера qδ4 представляющий правильную форму с удаленными тремя четвертями вершин и содержащий симметрию Группа Коксетера для n ≥ 5 с = и для четверти n-кубических сот = .[1]
| qδп | Имя | Schläfli символ | Диаграммы Кокстера | Грани | Фигура вершины | ||
|---|---|---|---|---|---|---|---|
| qδ3 |  четверть квадратная черепица | q {4,4} |
| ч {4} = {2} | { }×{ } | { }×{ } | |
| qδ4 |  четверть кубических сот | q {4,3,4} |  ч {4,3} |  час2{4,3} | 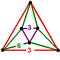 Удлиненный треугольная антипризма | ||
| qδ5 | четверть тессерактических сот | q {4,32,4} |  ч {4,32} |  час3{4,32} | {3,4}×{} | ||
| qδ6 | четверть 5 куб. соты | q {4,33,4} |  ч {4,33} |  час4{4,33} | 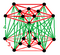 Выпрямленный 5-элементный антипризма | ||
| qδ7 | четверть 6 куб. соты | q {4,34,4} |  ч {4,34} |  час5{4,34} | {3,3}×{3,3} | ||
| qδ8 | четверть 7 куб. соты | q {4,35,4} |  ч {4,35} | 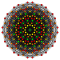 час6{4,35} | {3,3}×{3,31,1} | ||
| qδ9 | четверть 8 куб. соты | q {4,36,4} |  ч {4,36} |  час7{4,36} | {3,3}×{3,32,1} {3,31,1}×{3,31,1} | ||
| qδп | четверть n-кубических сот | q {4,3п-3,4} | ... | ч {4,3п-2} | часп-2{4,3п-2} | ... | |
Смотрите также
- Гиперкубические соты
- Чередующиеся гиперкубические соты
- Простые соты
- Усеченные простые соты
- Простые усеченные соты
Рекомендации
- ^ Кокстер, Обычные и полурегулярные соты, 1988, стр. 318-319.
- Кокстер, H.S.M. Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
- С. 122–123, 1973. (Решетка гиперкубов γп сформировать кубические соты, δп + 1)
- стр. 154–156: Частичное усечение или чередование, представленное q префикс
- п. 296, Таблица II: Обычные соты, δп + 1
- Калейдоскопы: избранные произведения Х. С. М. Коксетер, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Однородные заполнители пространств)
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45] См. Стр. 318. [2]
- Клитцинг, Ричард. «Евклидовы мозаики 1D-8D».
| Космос | Семья | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Равномерная черепица | {3[3]} | δ3 | hδ3 | qδ3 | Шестиугольный |
| E3 | Равномерно выпуклые соты | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Равномерные 4-соты | {3[5]} | δ5 | hδ5 | qδ5 | 24-ячеечные соты |
| E5 | Равномерные 5-соты | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Равномерные 6-соты | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Равномерные 7-соты | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Равномерные 8-соты | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Равномерные 9-соты | {3[10]} | δ10 | hδ10 | qδ10 | |
| Eп-1 | Униформа (п-1)-соты | {3[n]} | δп | hδп | qδп | 1k2 • 2k1 • k21 |











