Ректифицированные тессерактические соты - Rectified tesseractic honeycomb

четверть кубических сот
(Нет изображения)
Тип	Равномерные 4-соты
Семья	Четверть гиперкубические соты
Символ Шлефли	г {4,3,3,4} г {4,31,1} г {4,31,1} q {4,3,3,4}
Диаграмма Кокстера-Дынкина	= = = =
4-гранный тип	ч {4,32}, час3{4,32},
Тип ячейки	{3,3}, т1{4,3},
Тип лица	{3} {4}
Край фигура	Квадратная пирамида
Фигура вершины	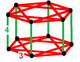Удлиненный {3,4}×{}
Группа Кокстера	${ displaystyle { tilde {C}} _ ​​{4}}$ = [4,3,3,4] ${ displaystyle { tilde {B}} _ {4}}$ = [4,31,1] ${ displaystyle { tilde {D}} _ {4}}$ = [31,1,1,1]
Двойной
Характеристики	вершинно-транзитивный

В четырехмерный Евклидова геометрия, то ректифицированные тессерактические соты равномерное заполнение пространства мозаика (или же соты ) в 4-мерном евклидовом пространстве. Он построен исправление из тессерактические соты который создает новые вершины в середине всех исходных ребер, выпрямляя ячейки в исправленные тессеракты и добавив новые 16 ячеек фасеты в исходных вершинах. Его вершина фигуры является восьмигранная призма, {3,4}×{}.

Его также называют четверть тессерактических сот так как он имеет половину вершин 4-полукубические соты, а четверть вершин тессерактические соты.^[1]

Связанные соты

[4,3,3,4], , Группа Кокстера генерирует 31 перестановку однородных мозаик, 21 с четкой симметрией и 20 с четкой геометрией. В расширенный Тессерактические соты (также известные как стерилизованные тессерактические соты) геометрически идентичны тессерактическим сотам. Три симметричные соты относятся к семейству [3,4,3,3]. Два чередования (13) и (17), а также четверть тессерактика (2) повторяются в других семействах.

C4 соты
Расширенный симметрия	Расширенный диаграмма	Заказ	Соты
[4,3,3,4]:		×1	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
[[4,3,3,4]]		×2	(1), (2), (13), 18 (6), 19, 20
[(3,3)[1+,4,3,3,4,1+]] ↔ [(3,3)[31,1,1,1]] ↔ [3,4,3,3]	↔ ↔	×6	14, 15, 16, 17

[4,3,3^1,1], , Группа Кокстера генерирует 31 перестановку однородных мозаик, 23 с четкой симметрией и 4 с отличной геометрией. Есть две чередующиеся формы: чередования (19) и (24) имеют ту же геометрию, что и 16-ячеечные соты и курносый 24-элементный сотовый соответственно.

В4 соты
Расширенный симметрия	Расширенный диаграмма	Заказ	Соты
[4,3,31,1]:		×1	5, 6, 7, 8
<[4,3,31,1]>: ↔[4,3,3,4]	↔	×2	9, 10, 11, 12, 13, 14, (10), 15, 16, (13), 17, 18, 19
[3[1+,4,3,31,1]] ↔ [3[3,31,1,1]] ↔ [3,3,4,3]	↔ ↔	×3	1, 2, 3, 4
[(3,3)[1+,4,3,31,1]] ↔ [(3,3)[31,1,1,1]] ↔ [3,4,3,3]	↔ ↔	×12	20, 21, 22, 23

Есть десять однородных сот построенный ${ displaystyle { tilde {D}} _ {4}}$ Группа Кокстера, все повторяется в других семействах по расширенной симметрии, что видно по графической симметрии колец в Диаграммы Кокстера – Дынкина. 10-й построен как чередование. Как подгруппы в Обозначение Кокстера: [3,4,(3,3)^*] (индекс 24), [3,3,4,3^*] (индекс 6), [1⁺,4,3,3,4,1⁺] (индекс 4), [3^1,1,3,4,1⁺] (индекс 2) все изоморфны [3^1,1,1,1].

Десять перестановок перечислены с их высшим расширенным отношением симметрии:

D4 соты
Расширенный симметрия	Расширенный диаграмма	Расширенный группа	Соты
[31,1,1,1]		${ displaystyle { tilde {D}} _ {4}}$	(никто)
<[31,1,1,1]> ↔ [31,1,3,4]	↔	${ displaystyle { tilde {D}} _ {4}}$×2 = ${ displaystyle { tilde {B}} _ {4}}$	(никто)
<2[1,131,1]> ↔ [4,3,3,4]	↔	${ displaystyle { tilde {D}} _ {4}}$×4 = ${ displaystyle { tilde {C}} _ ​​{4}}$	1, 2
[3[3,31,1,1]] ↔ [3,3,4,3]	↔	${ displaystyle { tilde {D}} _ {4}}$×6 = ${ displaystyle { tilde {F}} _ {4}}$	3, 4, 5, 6
[4[1,131,1]] ↔ [[4,3,3,4]]	↔	${ displaystyle { tilde {D}} _ {4}}$×8 = ${ displaystyle { tilde {C}} _ ​​{4}}$×2	7, 8, 9
[(3,3)[31,1,1,1]] ↔ [3,4,3,3]	↔	${ displaystyle { tilde {D}} _ {4}}$×24 = ${ displaystyle { tilde {F}} _ {4}}$
[(3,3)[31,1,1,1]]+ ↔ [3+,4,3,3]	↔	½${ displaystyle { tilde {D}} _ {4}}$×24 = ½${ displaystyle { tilde {F}} _ {4}}$	10

Смотрите также

Регулярные и однородные соты в 4-м пространстве:

• Тессерактические соты
• Димитессератические соты
• 24-ячеечные соты
• Усеченный 24-элементный сотовый
• Сота с 24 ячейками
• 5-ячеечные соты
• Усеченные 5-ячеечные соты
• Усеченные 5-ячеечные соты

Примечания

Рекомендации

• Калейдоскопы: избранные произведения Х. С. М. Коксетер, отредактированный Ф. Артуром Шерком, Питером Макмалленом, Энтони С. Томпсоном, Азией Ивичем Вайс, публикацией Wiley-Interscience, 1995, ISBN  978-0-471-01003-6 [1]
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45] См. Стр. 318. [2]
• Георгий Ольшевский, Однородные паноплоидные тетракомбы, Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
• Клитцинг, Ричард. "4D Евклидовы мозаики # 4D". o4x3o3o4o, o3o3o * b3x4o, x3o3x * b3o4o, x3o3x * b3o * b3o - риттит - O87
• Конвей Дж. Х., Слоан Нью-Джерси (1998). Сферические упаковки, решетки и группы (3-е изд.). ISBN  0-387-98585-9.

Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${ displaystyle { tilde {A}} _ {n-1}}$	${ displaystyle { tilde {C}} _ ​​{n-1}}$	${ displaystyle { tilde {B}} _ {n-1}}$	${ displaystyle { tilde {D}} _ {n-1}}$	${ displaystyle { tilde {G}} _ {2}}$ / ${ displaystyle { tilde {F}} _ {4}}$ / ${ displaystyle { tilde {E}} _ {n-1}}$
E2	Равномерная черепица	{3[3]}	δ3	hδ3	qδ3	Шестиугольный
E3	Равномерно выпуклые соты	{3[4]}	δ4	hδ4	qδ4
E4	Равномерные 4-соты	{3[5]}	δ5	hδ5	qδ5	24-ячеечные соты
E5	Равномерные 5-соты	{3[6]}	δ6	hδ6	qδ6
E6	Равномерные 6-соты	{3[7]}	δ7	hδ7	qδ7	222
E7	Равномерные 7-соты	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Равномерные 8-соты	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Равномерные 9-соты	{3[10]}	δ10	hδ10	qδ10
Eп-1	Униформа (п-1)-соты	{3[n]}	δп	hδп	qδп	1k2 • 2k1 • k21