Усеченный 24-элементный сотовый - Truncated 24-cell honeycomb

Усеченный 24-элементный сотовый
(Нет изображения)
Тип	Равномерные 4-соты
Символ Шлефли	т {3,4,3,3} tr {3,3,4,3} t2r {4,3,3,4} t2r {4,3,31,1} т {31,1,1,1}
Диаграммы Кокстера-Дынкина
4-гранный тип	Тессеракт Усеченный 24-элементный
Тип ячейки	Куб Усеченный октаэдр
Тип лица	Квадрат Треугольник
Фигура вершины	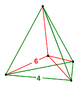Тетраэдрическая пирамида
Группы Кокстера	${ displaystyle { tilde {F}} _ {4}}$, [3,4,3,3] ${ displaystyle { tilde {B}} _ {4}}$, [4,3,31,1] ${ displaystyle { tilde {C}} _ ​​{4}}$, [4,3,3,4] ${ displaystyle { tilde {D}} _ {4}}$, [31,1,1,1]
Характеристики	Вершина транзитивная

В четырехмерный Евклидова геометрия, то усеченный 24-элементный сотовый равномерное заполнение пространства соты. Это можно рассматривать как усечение регулярного 24-ячеечные соты, содержащий тессеракт и усеченный 24-элементный клетки.

Имеет униформу чередование, называется курносый 24-элементный сотовый. Это пренебрежение со стороны ${ displaystyle { tilde {D}} _ {4}}$ строительство. Этот усеченный 24-элементный Символ Шлефли т {3^1,1,1,1}, и это пренебрежительно представлен как s {3^1,1,1,1}.

Альтернативные имена

• Усеченный икозитетрахорический тетракомб
• Усеченные икозитетрахорические соты
• Усеченные 16-ячеечные соты
• Двухслойные усеченные тессерактические соты

Построения симметрии

Есть пять различных конструкций симметрии этой мозаики. Каждая симметрия может быть представлена ​​различным расположением цветных усеченный 24-элементный грани. Во всех случаях четыре усеченных 24-ячейки и одна тессеракт встречаются в каждой вершине, но фигуры вершин имеют разные генераторы симметрии.

Группа Кокстера	Coxeter диаграмма	Грани	Фигура вершины	Вершина фигура симметрия (порядок)
${ displaystyle { tilde {F}} _ {4}}$ = [3,4,3,3]		4: 1:		, [3,3] (24)
${ displaystyle { tilde {F}} _ {4}}$ = [3,3,4,3]		3: 1: 1:		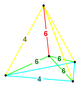, [3] (6)
${ displaystyle { tilde {C}} _ ​​{4}}$ = [4,3,3,4]		2,2: 1:		, [2] (4)
${ displaystyle { tilde {B}} _ {4}}$ = [31,1,3,4]		1,1: 2: 1:		, [ ] (2)
${ displaystyle { tilde {D}} _ {4}}$ = [31,1,1,1]		1,1,1,1: 1:		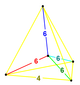[ ]+ (1)

Смотрите также

Обычные и однородные соты в 4-х пространстве:

• Тессерактические соты
• 16-ячеечные соты
• 24-ячеечные соты
• Ректифицированный 24-элементный сотовый
• Сота с 24 ячейками
• 5-ячеечные соты
• Усеченные 5-ячеечные соты
• Усеченные 5-ячеечные соты

Рекомендации

• Кокстер, H.S.M. Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN  0-486-61480-8 п. 296, Таблица II: Обычные соты
• Калейдоскопы: избранные произведения Х. С. М. Коксетер, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN  978-0-471-01003-6 [1]
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
• Георгий Ольшевский, Однородные паноплоидные тетракомбы, Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб) Модель 99
• Клитцинг, Ричард. «4D евклидова мозаика». o4x3x3x4o, x3x3x * b3x4o, x3x3x * b3x * b3x, o3o3o4x3x, x3x3x4o3o - тикот - O99

v т е Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${ displaystyle { tilde {A}} _ {n-1}}$	${ displaystyle { tilde {C}} _ ​​{n-1}}$	${ displaystyle { tilde {B}} _ {n-1}}$	${ displaystyle { tilde {D}} _ {n-1}}$	${ displaystyle { tilde {G}} _ {2}}$ / ${ displaystyle { tilde {F}} _ {4}}$ / ${ displaystyle { tilde {E}} _ {n-1}}$
E2	Равномерная черепица	{3[3]}	δ3	hδ3	qδ3	Шестиугольный
E3	Равномерно выпуклые соты	{3[4]}	δ4	hδ4	qδ4
E4	Равномерные 4-соты	{3[5]}	δ5	hδ5	qδ5	24-ячеечные соты
E5	Равномерные 5-соты	{3[6]}	δ6	hδ6	qδ6
E6	Равномерные 6-соты	{3[7]}	δ7	hδ7	qδ7	222
E7	Равномерные 7-соты	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Равномерные 8-соты	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Равномерные 9-соты	{3[10]}	δ10	hδ10	qδ10
Eп-1	Униформа (п-1)-соты	{3[n]}	δп	hδп	qδп	1k2 • 2k1 • k21