Гирихская плитка - Girih tiles

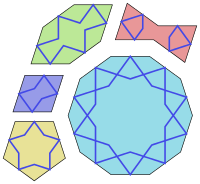
Гирих плитка
Узорчатый Гирих плитка
Строительные линии обычно скрыты: слева геометрическая плитка, гирих узор справа.

Гирих плитка набор из пяти плитка которые были использованы при создании Исламские геометрические узоры с помощью ремни (гирих ) для отделки зданий в Исламская архитектура. Они использовались примерно с 1200 года, и их устройство значительно улучшилось, начиная с Дарб-и Имам святыня в Исфахан в Иран Построен в 1453 году.

Пять плиток

Пять форм плитки:

  • обычный десятиугольник с десятью внутренними углами 144 °;
  • удлиненный (неправильный выпуклый) шестиугольник с внутренними углами 72 °, 144 °, 144 °, 72 °, 144 °, 144 °;
  • а галстук-бабочка (невыпуклый шестиугольник) с внутренними углами 72 °, 72 °, 216 °, 72 °, 72 °, 216 °;
  • а ромб с внутренними углами 72 °, 108 °, 72 °, 108 °; и
  • обычный пятиугольник с пятью внутренними углами 108 °.

У этих модулей есть свои специфические Персидский имена: четырехугольная плитка называется Торандж, пятиугольная плитка называется Панге, вогнутая восьмиугольная плитка называется Шеш Бэнд, плитка с галстуком-бабочкой называется Сормех Дан, а декаграмма называется Табл.[1] Все стороны этих фигур имеют одинаковую длину, а все их углы кратны 36 ° (π / 5 радианы ). Все они, кроме пятиугольника, обладают двусторонней (отражающей) симметрией через две перпендикулярные линии. У некоторых есть дополнительные симметрии. В частности, десятиугольник имеет десятикратное вращательная симметрия (поворот на 36 °); а пятиугольник имеет пятикратную симметрию вращения (поворот на 72 °).

Появление плитки гирих

К концу 11 века исламские художники Северной Африки начали использовать «мозаика из плитки ”, Который является предшественником мозаика.[2] К 13 веку, благодаря развитию арифметических вычислений и геометрии, мусульмане открыли новый способ построения «мозаики из плиток» - плитки гирих.[3]

Гирих

Основная статья: Гирих

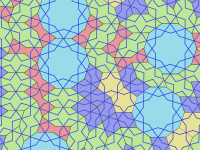
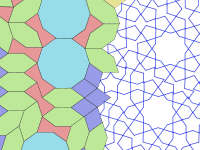
Гирих линии (ремни ), которые украшают плитку. Плитка используется для формирования узоров гирих, начиная с Персидский слово گره, что означает «узел».[4] В большинстве случаев видны только гирих (и другие мелкие украшения, например цветы), а не границы самих плиток. Гири - это кусочные прямые линии, пересекающие границы плиток в центре края под углом 54 ° (3π / 10 радиан) к краю. Два пересекающихся гириха пересекают каждый край плитки. Большинство плиток имеют уникальный узор гирих внутри плитки, который является непрерывным и повторяет симметрию плитки. Однако у десятиугольника есть два возможных образца гирих, один из которых имеет только пятикратную, а не десятикратную вращательную симметрию.

Математика гирихских мозаик

В 2007 году физики Питер Дж. Лу и Пол Дж. Стейнхардт предположил, что мозаики гирих обладают свойствами, соответствующими самоподобный фрактал квазикристаллический плитки, такие как Мозаики Пенроуза, опередив их на пять веков.[5][6]

Этот вывод был подтвержден как анализом узоров на сохранившихся структурах, так и исследованием персидских свитков 15-го века. Нет никаких указаний на то, насколько больше архитекторы могли знать о задействованной математике. Обычно считается, что такие конструкции были построены путем рисования зигзагообразных контуров с помощью только линейки и циркуля. Шаблоны, которые можно найти на свитках, например, 97 футов (29,5 метра) длиной Свиток Топкапы возможно, были проконсультированы. Найдено в Дворец Топкапы в Стамбуле, административном центре Османской империи, датируемом концом 15 века, свиток показывает последовательность двух- и трехмерных геометрических узоров. Текст отсутствует, но есть сетка и цветовое кодирование, используемые для выделения симметрии и различения трехмерных проекций. Рисунки, подобные изображенным на этом свитке, могли служить в качестве сборников выкроек для мастеров, которые изготавливали плитки, а форма плиток гирих диктовала, как их можно объединить в большие узоры. Таким образом, мастера могли создавать очень сложные конструкции, не прибегая к математике и не обязательно понимая их основные принципы.[7]

Такое использование повторяющихся узоров, созданных из ограниченного числа геометрических фигур, доступных мастерам того времени, похоже на практику современных европейских Готика ремесленники. Дизайнеры обоих стилей стремились использовать свой инвентарь геометрических форм для создания максимального разнообразия форм. Это требовало навыков и практики, очень отличных от математики.[7]

Геометрическое построение взаимосвязанной мозаики из декаграммы и многоугольника

Сначала разделите прямой угол A на пять частей равного градуса, создав четыре луча, которые начинаются из A. Найдите произвольную точку C на втором луче и опустите перпендикуляры от C к сторонам угла A против часовой стрелки. На этом шаге создается прямоугольник ABCD вместе с четырьмя сегментами, каждый из которых имеет конечную точку в точке A; другие конечные точки - это пересечения четырех лучей с двумя сторонами BC и DC прямоугольника ABCD. Затем найдите середину четвертого сегмента, созданного из точки четвертого луча E. Постройте дугу с центром A и радиусом AE, чтобы пересечь AB в точке F и второй луч в точке G. Второй сегмент теперь является частью прямоугольника. диагональ. Проведите линию, параллельную AD и проходящую через точку G, которая пересекает первый луч в точке H и третий луч в точке I. Прямая HF проходит через точку E и пересекает третий луч в точке L и линию AD в точке J. Постройте прямую. проходящий через точку J, параллельную третьему лучу. Также постройте линию EI и найдите M, который является пересечением этой прямой с AD. Из точки F проведите параллельную линию к третьему лучу, чтобы он встретился с первым лучом в точке K. Постройте отрезки GK, GL и EM. Найдите точку N такую, что GI = IN, построив окружность с центром I и радиусом IG. Постройте прямую DN, которая параллельна GK, чтобы пересечь линию, исходящую из J, и найдите P, чтобы завершить правильный пятиугольник EINPJ. Прямая DN пересекает серединный перпендикуляр к AB в точке Q. Из Q постройте прямую, параллельную FK, чтобы пересечь луч MI в точке R. Как показано на рисунке, используя точку O, которая является центром прямоугольника ABCD, в качестве центра вращения на 180 °. , можно составить фундаментальную область для замощения.[1]

Переплетенная мозаика из декаграммы и многоугольника
Переплетенная мозаика из декаграммы и многоугольника
Переплетенная мозаика из декаграммы и многоугольника
Переплетенная мозаика из декаграммы и многоугольника

Геометрическое построение мозаики из архитектурных свитков Мирзы Акбара

Сначала разделите прямой угол на пять равных углов. На первом луче выбирается произвольная точка P против часовой стрелки. Для радиуса круга, вписанного в декаграмму, выбирается половина сегмента, образованного из третьего луча, сегмента AM. На следующем рисунке показано пошаговое визуальное решение проблемы автором с помощью линейки и компаса.[1] Обратите внимание, что способ разделить прямой угол на пять совпадающих углов не входит в состав предоставленных инструкций, потому что это считается элементарным шагом для дизайнеров.

Пошаговое построение тесселяции циркулем-линейкой

Примеры

  • Различные узоры

  • Сложные узоры гирих с 16-, 10- и 8-балльными звездами в разных масштабах на потолке Могила Хафеза в Шираз, 1935

  • Окно квартиры наследного принца в Дворец Топкапы, Стамбул, Турция, с 6-балльными звездами; обрамление выложено плиткой в ​​стиле арабески с цветочными мотивами

  • Внутренняя арка на открытии ложи султана в Османской империи Зеленая мечеть в Бурса, Турция (1424 г.), с 10-конечными звездами и пятиугольниками

Гирих широко применяется в архитектуре. Гирих на персидских геометрических окнах отвечает требованиям персидской архитектуры. Особые виды украшений, используемых в ороси, обычно связывали окна с социальным и политическим авторитетом покровителя. Чем декоративнее окно, тем выше вероятность того, что его владелец будет иметь более высокий социальный и экономический статус. Хорошим примером этого является Азад Колиджи, сад Довлатабад в Иране. Узоры гирих на его окне успешно демонстрируют несколько слоев. Первый слой - это настоящий сад, который люди могут увидеть, открыв окно. Затем есть первый узор гирих снаружи окна, резной узор. Другой искусственный слой - это разноцветное стекло окна, разноцветные слои которого создают ощущение массы цветов. Этот абстрактный слой явно противоречит реальному слою за окном и дает простор для воображения.[8]

Смотрите также

Рекомендации

  1. ^ а б c Сарханги, Реза (2012). «Переплетение звездных многоугольников в персидской архитектуре: особый случай декаграммы в мозаичных рисунках». Nexus Netw J. 14 (2). п. 350. Дои:10.1007 / s00004-012-0117-5.
  2. ^ Hattstein / Delius., Markus / Peter (2013). Ислам: искусство и архитектура. Потсдам: Х.Ф. Ульманн. п. 448. ISBN  978-3848003808.
  3. ^ Лу, П. Дж .; Стейнхардт, П. Дж. (2007). «Десятиугольные и квазикристаллические плитки в средневековой исламской архитектуре». Наука. 315 (5815): 1106–1110. Bibcode:2007Научный ... 315.1106Л. Дои:10.1126 / science.1135491. JSTOR  20039057. PMID  17322056. S2CID  10374218.
  4. ^ Себастьян Р. Прейндж (сентябрь – октябрь 2009 г.). "Плитки бесконечности". Saudi Aramco World: 24–31. Архивировано из оригинал на 13.01.2010. Получено 2010-01-08.
  5. ^ Питер Дж. Лу и Пол Дж. Стейнхардт (2007). «Десятиугольные и квазикристаллические плитки в средневековой исламской архитектуре». Наука. 315 (5815): 1106–1110. Bibcode:2007Научный ... 315.1106Л. Дои:10.1126 / science.1135491. PMID  17322056. S2CID  10374218.
  6. ^ Дополнительные цифры
  7. ^ а б Гулру Нечипоглу (1995). Свиток Топкапы: геометрия и орнамент в исламской архитектуре. Исследовательский институт Гетти.
  8. ^ Колиджи, Хуман (2015). «Построенный на свете:« Искусное »искусство окон с геометрическим узором». Международный журнал исламской архитектуры. 4: 75–108. Дои:10.1007 / s00004-016-0288-6.

внешняя ссылка