Математика и искусство - Википедия - Mathematics and art

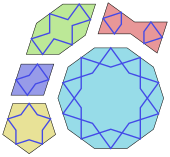
Математика и искусство связаны по-разному. Математика сам был описан как Изобразительное искусство движимый красотой. Математику можно различить в таких искусствах, как Музыка, танцевать, картина, архитектура, скульптура, и текстиль. Однако эта статья посвящена математике в изобразительном искусстве.
Математика и искусство имеют давние исторические отношения. Художники использовали математику с 4 века до нашей эры, когда греческий скульптор Поликлет написал его Canon, прописывая пропорции предположительно было основано по соотношению 1:√2 для идеального мужского ню. В народе настойчиво утверждается, что использование Золотое сечение в античном искусстве и архитектуре без достоверных свидетельств. В итальянском эпоха Возрождения, Лука Пачоли написал влиятельный трактат De Divina пропорционально (1509), иллюстрировано гравюрами на дереве Леонардо да Винчи, об использовании золотого сечения в искусстве. Другой итальянский художник, Пьеро делла Франческа, развитый Евклид идеи о перспектива в трактатах, таких как De Prospectiva Pingendi, и в его картинах. Гравер Альбрехт Дюрер сделал много ссылок на математику в своей работе Меленколия I. В наше время художник-график М. К. Эшер интенсивно использовали мозаика и гиперболическая геометрия, с помощью математика Х. С. М. Коксетер, в то время как Де Стейл движение во главе с Тео ван Дусбург и Пит Мондриан явно охватил геометрические формы. Математика вдохновила текстильное искусство, такое как квилтинг, Вязание, вышивка крестиком, вязание крючком, вышивка, ткачество, турецкий и другие ковер -изготовление, а также килим. В Исламское искусство, симметрии очевидны в таких разнообразных формах, как персидские гирих и марокканский Zellige плитка Могол Джали перфорированные каменные ширмы и широко распространенные Мукарнас прыжки.
Математика напрямую повлияла на искусство с помощью таких концептуальных инструментов, как линейная перспектива, анализ симметрия, и математические объекты, такие как многогранники и Лента Мебиуса. Магнус Веннингер создает красочные звездчатые многогранники, первоначально как модели для обучения. Математические понятия, такие как рекурсия и логический парадокс можно увидеть в картинах Рене Магритт и гравюры М. К. Эшера. Компьютерное искусство часто использует фракталы в том числе Набор Мандельброта, а иногда исследует другие математические объекты, такие как клеточные автоматы. Спорно, художник Дэвид Хокни утверждал, что художники эпохи Возрождения и далее использовали камера lucida рисовать точные изображения сцен; архитектор Филип Стедман аналогичным образом утверждал, что Вермеер использовал камера-обскура в его отчетливо наблюдаемых картинах.
Другие взаимосвязи включают алгоритмический анализ произведений искусства Рентгеновская флуоресцентная спектроскопия, открытие, что традиционные батики из разных регионов Ява иметь четкие фрактальные измерения, и стимулы к математическим исследованиям, особенно Филиппо Брунеллески теории перспективы, которая в конечном итоге привела к Жирар Дезарг с проективная геометрия. Настойчивое мнение, основанное, в конечном счете, на Пифагорейский понятие гармонии в музыке, считает, что все было устроено Числом, что Бог является геометром мира, и, следовательно, мир геометрия священна.
Истоки: от Древней Греции до эпохи Возрождения
Поликлита Canon и симметрия
Поликлет старший (ок. 450–420 до н. э.) был Греческий скульптор из школы Аргос, и современник Фидий. Его работы и статуи состояли в основном из бронзы и изображали спортсменов. По мнению философа и математика Ксенократ, Поликлет считается одним из самых выдающихся скульпторов классическая древность за его работу над Дорифор и статуя Гера в Герайон Аргосский.[3] Хотя его скульптуры не так известны, как скульптуры Фидия, ими очень восхищаются. в его канон, трактат, который он написал, чтобы задокументировать "идеальный" пропорции тела Поликлетос дает нам математический подход к моделированию человеческого тела.[3]
В Canon сам по себе был утерян, но предполагается, что Поликлет использовал последовательность пропорций, где каждая длина равна диагонали квадрата, нарисованного на его предшественнике, 1:√2 (примерно 1: 1.1412).[4]
Влияние Canon Поликлета огромен в Классический греческий, Римский, и эпоха Возрождения скульптуры, многие скульпторы следуют рецепту Поликлета. Хотя ни одна из оригинальных работ Поликлета не сохранилась, римские копии демонстрируют его идеал физического совершенства и математической точности. Некоторые ученые утверждают, что Пифагорейский мысль повлияла на Canon Поликлета.[5] В Canon применяет основные математические концепции греческой геометрии, такие как соотношение, пропорции и симметрия (По-гречески «гармоничные пропорции») и превращает его в систему, способную описывать человеческую форму через серию непрерывных геометрические прогрессии.[4]
Перспектива и пропорции

В классические времена вместо того, чтобы уменьшать далекие фигуры с помощью линейная перспектива, художники определяли размеры предметов и фигур в соответствии с их тематической важностью. В средние века некоторые художники использовали обратная перспектива для особого акцента. Мусульманский математик Альхазен (Ибн аль-Хайтам) описал теорию оптики в своем Книга оптики в 1021 г., но никогда не относился к искусству.[6] В эпоху Возрождения возродилась классическая греческая и римская культура и идеи, в том числе изучение математики для понимания природа и искусство. Два основных мотива подтолкнули художников позднего средневековья и эпохи Возрождения к математике. Во-первых, художникам нужно было придумать, как изобразить трехмерные сцены на двухмерном холсте. Во-вторых, как философы, так и художники были убеждены, что математика является истинной сущностью физического мира и что всю вселенную, включая искусства, можно объяснить в геометрических терминах.[7]
Зачатки перспективы пришли с Джотто (1266/7 - 1337), которые пытались рисовать в перспективе, используя алгебраический метод для определения расположения удаленных линий. В 1415 году итальянский архитектор Филиппо Брунеллески и его друг Леон Баттиста Альберти продемонстрировал геометрический метод применения перспективы во Флоренции, используя похожие треугольники как сформулировал Евклид, чтобы найти видимую высоту далеких объектов.[8][9] Перспективные картины Брунеллески потеряны, но Мазаччо Картина Святой Троицы показывает его принципы в действии.[6][10][11]

Итальянский художник Паоло Уччелло (1397–1475) был очарован перспективой, как показано на его картинах Битва при Сан-Романо (ок. 1435–1460): сломанные копья удобно лежат вдоль перспективных линий.[12][13]
Художник Пьеро делла Франческа (ок. 1415–1492) стал примером этого нового сдвига в мышлении итальянского Возрождения. Он был экспертом математик и геометр, писать книги на сплошная геометрия и перспектива, включая De prospectiva pingendi (О перспективе живописи), Trattato d'Abaco (Трактат о абаках), и De quinque corporibus regularibus (О пяти правильных телах).[14][15][16] Историк Вазари в его Жизни художников называет Пьеро «величайшим геометром своего времени или, возможно, всех времен».[17] Интерес Пьеро к перспективе можно увидеть в его картинах, включая Полиптих Перуджи,[18] то Алтарь Сан-Агостино и Бичевание Христа. Его работы по геометрии повлияли на более поздних математиков и художников, включая Лука Пачоли в его De Divina пропорционально и Леонардо да Винчи. Пьеро изучал классическую математику и труды Архимед.[19] Его учили коммерческой арифметике в "школах счёта"; его сочинения отформатированы как школьные учебники на счетах,[20] возможно, включая Леонардо Пизано (Фибоначчи ) 1202 Liber Abaci. Линейная перспектива только вводился в художественный мир. Альберти объяснил в своем 1435 г. De pictura: "световые лучи проходят по прямым линиям от точек наблюдаемой сцены к глазу, образуя своего рода пирамида с глазом в качестве вершины ". Картина, построенная в линейной перспективе, является поперечное сечение этой пирамиды.[21]
В De Prospectiva Pingendi, Пьеро трансформирует свои эмпирические наблюдения за тем, как аспекты фигуры меняются с точки зрения точки зрения, в математические доказательства. Его трактат начинается в духе Евклида: он определяет точку как «малейшую вещь, которую может постичь глаз».[а][7] Он использует дедуктивная логика чтобы привести читателя к перспективному изображению трехмерного тела.[22]
Исполнитель Дэвид Хокни утверждал в его книге Тайные знания: открытие утерянных техник старых мастеров что художники начали использовать камера lucida с 1420-х годов, что привело к внезапному изменению точности и реализма, и эта практика была продолжена крупными художниками, включая Ingres, Ван Эйк, и Караваджо.[23] Критики расходятся во мнениях относительно того, был ли прав Хокни.[24][25] Точно так же архитектор Филип Стедман противоречиво утверждал.[26] который Вермеер использовал другое устройство, камера-обскура, чтобы помочь ему создать его отчетливо наблюдаемые картины.[27]
В 1509 г. Лука Пачоли (ок. 1447–1517) опубликовано De Divina пропорционально на математический и артистический пропорция, в том числе в человеческом лице. Леонардо да Винчи (1452–1519) иллюстрировал текст ксилографией правильных тел, когда учился у Пачоли в 1490-х годах. Рисунки Леонардо, вероятно, являются первыми иллюстрациями скелетных твердых тел.[28] Такие, как ромбокубооктаэдр, были одними из первых, кого нарисовали, чтобы продемонстрировать перспективу путем наложения друг на друга. В работе обсуждается перспектива в творчестве Пьеро делла Франческа, Мелоццо да Форли, и Марко Пальмеццано.[29] Да Винчи изучал Пачоли Сумма, из которого он скопировал таблицы пропорций.[30] В Мона Лиза и Тайная вечеря, Работы да Винчи включали линейную перспективу с точка схода чтобы обеспечить кажущуюся глубину.[31] Тайная вечеря построен в тесном соотношении 12: 6: 4: 3, как и Рафаэль с Афинская школа, который включает Пифагора с табличкой идеальных соотношений, священной для пифагорейцев.[32][33] В Витрувианский человек Леонардо выразил идеи римского архитектора Витрувий, новаторски показывая мужскую фигуру дважды и центрируя его как в круге, так и в квадрате.[34]
Еще в 15 веке криволинейная перспектива нашла свое отражение в картинах художников, заинтересованных в искажении изображения. Ян ван Эйк 1434 год Портрет Арнольфини содержит выпуклое зеркало с отражениями людей в сцене,[35] пока Пармиджанино с Автопортрет в выпуклом зеркале, c. 1523–1524 гг., В центре изображено почти неискаженное лицо художника с сильно изогнутым фоном и рукой художника по краю.[36]
Трехмерное пространство в искусстве может быть представлено убедительно, как в технический рисунок другими способами, кроме перспективы. Косые проекции, включая кавалерскую перспективу (использовавшуюся французскими военными художниками для изображения укреплений в 18 веке), постоянно и повсеместно использовались китайскими художниками с первого или второго века до 18 века. Китайцы переняли технику из Индии, а в Древнем Риме. Косая проекция встречается в японском искусстве, например, в Укиё-э картины Тории Киёнага (1752–1815).[37]

Ксилография из Лука Пачоли 1509 год De Divina пропорционально с равносторонний треугольник на человеческом лице

Камера люцида в использовании. Scientific American, 1879

Иллюстрация художника, использующего камера-обскура. 17-го века

Пропорция: Леонардо с Витрувианский человек, c. 1490

Брунеллески теория перспектива: Мазаччо с Тринита, c. 1426–1428 гг., В Базилика Санта Мария Новелла

Диаграмма из Леон Баттиста Альберти 1435 год Делла Питтура, с колоннами в перспективе на сетке

Линейная перспектива в Пьеро делла Франческа с Бичевание Христа, c. 1455–1460

Пармиджанино, Автопортрет в выпуклом зеркале, c. 1523–1524

Пифагор с табличкой соотношений, в Рафаэль с Афинская школа, 1509

Косая проекция: Подъезд и двор яменя. Деталь прокрутки о Сучжоу Сюй Ян, заказанный Цяньлун Император. 18-ый век

Косая проекция: женщины играют Сёги, Идти и Бан-сугороку настольные игры. Живопись Тории Киёнага, Япония, гр. 1780 г.
Золотое сечение
В Золотое сечение (примерно 1,618) было известно Евклид.[38] Золотое сечение настойчиво утверждается[39][40][41][42] в наше время использовались в искусстве и архитектура древними в Египте, Греции и других местах без надежных доказательств.[43] Это утверждение может быть связано с путаницей с «золотой серединой», которая для древних греков означала «избегание излишеств в любом направлении», а не соотношение.[43] Пирамидологи с девятнадцатого века спорили на сомнительных математических основаниях золотого сечения в дизайне пирамид.[b] В Парфенон, храм V века до нашей эры в Афинах, как утверждается, использовал золотое сечение в своих фасад и план этажа,[46][47][48] но и эти утверждения опровергаются измерениями.[43] В Великая мечеть Кайруана в Тунисе также утверждалось, что в дизайне используется золотое сечение,[49] но соотношение не появляется в оригинальных частях мечети.[50] Историк архитектуры Фредерик Макоди Лунд утверждал в 1919 году, что Шартрский собор (12 век), Нотр-Дам Лаона (1157–1205) и Собор Парижской Богоматери (1160) разработаны в соответствии с Золотое сечение,[51] рисование линий регулятора, чтобы сделать его случай. Другие ученые утверждают, что до работы Пачоли в 1509 году золотое сечение было неизвестно художникам и архитекторам.[52] Например, высота и ширина фасада Нотр-Дам в Лаоне имеют соотношение 8/5 или 1,6, а не 1,618. Такой Отношения Фибоначчи быстро становится трудно отличить от золотого сечения.[53] После Пачоли золотое сечение более заметно в произведениях искусства, включая работы Леонардо. Мона Лиза.[54]
Другое соотношение, единственное другое морфическое число,[55] был назван пластиковый номер[c] в 1928 году голландским архитектором Ханс ван дер Лаан (первоначально названный Le Nombre Radiant На французском).[56] Его значение - решение кубическое уравнение
- ,
иррациональное число, равное примерно 1,325. По словам архитектора Ричард Падован, это имеет характерные соотношения 3/4 и 1/7, которые определяют пределы человеческого восприятия в отношении одного физического размера к другому. Ван дер Лаан использовал эти соотношения при разработке модели 1967 года. Аббатство Святого Бенедиктусберга церковь в Нидерландах.[56]

База: отношения гипотенузы (b: a) для Пирамида Хуфу может быть: 1: φ (Треугольник Кеплера ), 3:5 (3-4-5 Треугольник ), или 1: 4 / π

Предполагаемые соотношения: Нотр-Дам Лаона

Золотые прямоугольники наложены на Мона Лиза

1967 год Аббатство Святого Бенедиктусберга церковь Ханс ван дер Лаан имеет пластиковый номер пропорции.
Плоские симметрии

Плоские симметрии тысячелетиями использовались в таких произведениях искусства, как ковры, решетки, текстиль и плитка.[58][59][60][61]
Многие традиционные коврики, будь то ворсовые или плоские коврики. килимы, разделены на центральное поле и рамку; оба могут иметь симметрию, хотя в коврах ручной работы они часто слегка нарушены мелкими деталями, вариациями рисунка и изменениями цвета, внесенными ткачихой.[58] В килимах от Анатолия, то мотивы сами по себе обычно симметричны. Обычно присутствует и общая компоновка с такими схемами, как полосы, полосы, чередующиеся с рядами мотивов, и упакованные массивы примерно шестиугольных мотивов. Поле обычно выкладывается в виде обоев с группа обоев например, pmm, а граница может быть выложена как фриз из группа фризов pm11, pmm2 или pma2. Турецкие и среднеазиатские килимы часто имеют три и более границ в разных группах фризов. Ткачи, безусловно, стремились к симметрии, не зная ее математики.[58]Математик и теоретик архитектуры Никос Салингарос предполагает, что «мощное присутствие»[57] (эстетический эффект) "большого ковра"[57] такие как лучшие ковры с двумя медальонами из Коньи 17 века, созданы математическими методами, связанными с теориями архитектора. Кристофер Александр. Эти техники включают в себя создание пары противоположностей; противоположные значения цвета; геометрическое различение областей, будь то использование дополнительных форм или уравновешивание направленности острых углов; обеспечение мелкомасштабной сложности (от уровня узла и выше) и симметрии как малого, так и большого размера; повторяющиеся элементы в иерархии разных масштабов (с соотношением примерно 2,7 от каждого уровня к следующему). Салингарос утверждает, что «все успешные ковры удовлетворяют как минимум девяти из десяти вышеупомянутых правил», и предполагает, что можно создать метрику из этих правил.[57]
Сложные решетки встречаются в Индии. Джали работа, вырезанная из мрамора для украшения гробниц и дворцов.[59] Китайские решетки, всегда обладающие некоторой симметрией, существуют в 14 из 17 групп обоев; они часто имеют зеркальную, двойную зеркальную или вращательную симметрию. У некоторых есть центральный медальон, а у некоторых есть кайма в группе фризов.[62] Многие китайские решетки были проанализированы математически Дэниелом С. Даем; он определяет Сычуань как центр ремесла.[63]
Симметрии видны в текстильное искусство включая квилтинг,[60] Вязание,[64] вышивка крестиком, вязание крючком,[65] вышивка[66][67] и ткачество,[68] где они могут быть чисто декоративными или могут быть знаками статуса.[69] Вращательная симметрия встречается в круглых структурах, таких как купола; они иногда искусно украшены симметричными узорами внутри и снаружи, как в 1619 году. Мечеть шейха Лотфоллы в Исфахан.[70] Предметы вышивки и кружево скатерти и циновки, сделанные на шпульках или фриволите, может иметь широкий спектр симметрий отражения и вращения, которые исследуются математически.[71]
Исламское искусство использует симметрии во многих его художественных формах, особенно в гирих мозаики. Они сформированы с использованием набора из пяти форм плитки, а именно правильного десятиугольника, удлиненного шестиугольника, галстука-бабочки, ромба и правильного пятиугольника. Все стороны этих плиток имеют одинаковую длину; и все их углы кратны 36 ° (π / 5 радианы ), предлагая пяти- и десятикратную симметрию. Плитка украшена ремни линии (гирих), как правило, более заметны, чем границы плитки. В 2007 году физики Питер Лу и Пол Стейнхардт утверждал, что гирих напоминал квазикристаллический Мозаики Пенроуза.[72] Сложная геометрия Zellige плитка - отличительный элемент в Марокканский архитектура.[61] Мукарнас своды трехмерны, но спроектированы в двух измерениях с чертежами геометрических ячеек.[73]

Хотамис килим (деталь), центральный Анатолия, начало 19 века

Деталь Династия Мин парча, используя шестиугольная решетка с фаской шаблон

Джаали мраморная решетка на могиле Салим Чишти, Фатехпур Сикри, Индия

Симметрии: Флорентийский Узор Барджелло гобеленовая работа

Потолок Мечеть шейха Лотфоллы, Исфахан, 1619

Вращательная симметрия в кружево: фриволите работай
Гирихская плитка: узоры в крупном и мелком масштабе на шпандель от Дарб-и Имам святыня, Исфахан, 1453 г.

Мозаики: Zellige мозаика на Медресе Бу Инания, Фес, Марокко
Сложная геометрия и мозаики Мукарнас свод мечети Шейха Лотфоллаха в Исфахане
План архитектора свода квартала Мукарнас. Свиток Топкапы

Тупа Инка туника из Перу, 1450–1540, ан. Андский текстиль обозначающий высокий ранг[69]
Многогранники

В Платоновы тела и другие многогранники являются повторяющейся темой в западном искусстве. Они встречаются, например, в мраморной мозаике с изображением малый звездчатый додекаэдр, приписываемый Паоло Уччелло, на полу Базилика Сан-Марко в Венеции;[12] в диаграммах правильных многогранников Леонардо да Винчи, изображенных в качестве иллюстраций Лука Пачоли книга 1509 года Божественная пропорция;[12] как стакан ромбокубооктаэдр в портрете Пачоли Якопо де Барбари, написанном в 1495 году;[12] в усеченном многограннике (и различных других математических объектах) в Альбрехт Дюрер гравюра Меленколия I;[12] И в Сальвадор Дали картина Тайная вечеря в котором Христос и его ученики изображены внутри гигантского додекаэдр.[74]
Альбрехт Дюрер (1471–1528) был Немецкий эпоха Возрождения гравер внесший важный вклад в многогранную литературу в своей книге 1525 года, Underweysung der Messung (Обучение измерениям), предназначенные для обучения предметам линейная перспектива, геометрия в архитектура, Платоновы тела, и правильные многоугольники. Вероятно, на Дюрера повлияли работы Лука Пачоли и Пьеро делла Франческа во время его поездок в Италия.[75] Хотя примеры перспективы в Underweysung der Messung недоразвиты и содержат неточности, многогранники подробно обсуждаются. Дюрер также первым ввел в текст идею многогранные сети, многогранники развернуты, чтобы лежать плоско для печати.[76] Дюрер опубликовал еще одну влиятельную книгу о человеческие пропорции называется Vier Bücher von Menschlicher Proportion (Четыре книги о человеческих пропорциях) в 1528 г.[77]

Известная гравюра Дюрера Меленколия I изображает разочарованного мыслителя, сидящего у усеченный треугольный трапецоэдр и магический квадрат.[1] Эти два объекта и гравюра в целом были предметом более современной интерпретации, чем содержание почти любой другой гравюры.[1][80][81] в том числе двухтомник Петера-Клауса Шустера,[82] и влиятельная дискуссия в Эрвин Панофски монография Дюрера.[1][83]
Сальвадор Дали с Corpus Hypercubus изображает развернутую трехмерную сетку для гиперкуб, также известный как тессеракт; Разворачивание тессеракта в эти восемь кубов аналогично разворачиванию сторон куба в крестообразную форму из шести квадратов, здесь представляющих божественную перспективу с четырехмерным правильным многогранником.[79][78]
Фрактальные измерения

Традиционный индонезийский воск-резист батик рисунки на ткани комбайн репрезентативный мотивы (такие как цветочные и растительные элементы) с абстрактными и несколько хаотичными элементами, включая неточность в нанесении воскового резиста и случайные вариации, вызванные растрескиванием воска. В дизайне батика есть фрактальная размерность от 1 до 2, в зависимости от региона. Например, батик Чиребон имеет фрактальную размерность 1,1; батики Джокьякарта и Суракарта (Соло) в центре Ява иметь фрактальную размерность от 1,2 до 1,5; и батики Lasem на северном побережье Явы и Тасикмалая в Западной Яве фрактальная размерность составляет от 1,5 до 1,7.[84]
В капельная живопись работы современного художника Джексон Поллок одинаково различаются по своей фрактальной размерности. Его 1948 Число 14 имеет размерность 1,45, подобную береговой линии, в то время как его более поздние картины имели последовательно более высокие фрактальные измерения и, соответственно, более сложные узоры. Одна из его последних работ, Синие поляки, на создание ушло шесть месяцев, фрактальная размерность - 1,72.[85]
Сложные отношения
Астроном Галилео Галилей в его Il Saggiatore написал, что «[Вселенная] написана на язык математики, а его символы - треугольники, круги и другие геометрические фигуры ".[86] Художники, которые стремятся и стремятся изучать природу, должны, по мнению Галилея, прежде всего полностью понимать математику. Математики же, наоборот, стремились интерпретировать и анализировать искусство через призму геометрии и рациональности. Математик Фелипе Кукер предполагает, что математика, и особенно геометрия, является источником правил для «художественного творчества, основанного на правилах», хотя и не единственным.[87] Некоторые из многих составляющих сложных отношений[88] описаны ниже.

Математика как искусство
Математик Джерри П. Кинг описывает математику как искусство, заявляя, что «ключи к математике - это красота и элегантность, а не скучность и техническая сторона», и что красота является движущей силой математических исследований.[89] Кинг цитирует математика Г. Х. Харди Очерк 1940 года Извинения математика. В нем Харди обсуждает, почему он находит две теоремы классические времена как первоклассный, а именно Евклид доказательство того, что существует бесконечно много простые числа, и доказательство того, что квадратный корень из 2 равен иррациональный. Кинг оценивает последнее по критериям Харди для математическая элегантность: "серьезность, глубина, общность, неожиданность, неизбежность, и экономия(Курсив Кинга) и описывает доказательство как «эстетически приятное».[90] Венгерский математик Пол Эрдёш согласился с тем, что математика обладает красотой, но рассмотрел причины, не поддающиеся объяснению: «Почему числа красивы? Это все равно, что спрашивать, почему Девятая симфония Бетховена красивая. Если вы не понимаете почему, никто не может вам сказать. я знать числа прекрасны ".[91]
Математические инструменты для искусства
Математику можно найти во многих искусствах, таких как Музыка, танцевать,[92] картина, архитектура, и скульптура. Каждый из них тесно связан с математикой.[93] Помимо связи с изобразительным искусством, математика может предоставить художникам инструменты, такие как правила линейная перспектива как описано Брук Тейлор и Иоганн Ламберт, или методы начертательная геометрия, теперь применяется в программном моделировании твердых тел, начиная с Альбрехта Дюрера и Гаспар Монж.[94] Художники из Луки Пачоли в Средний возраст и Леонардо да Винчи и Альбрехт Дюрер в эпоха Возрождения использовали и развили математические идеи в творчестве.[93][95] Использование перспективы началось, несмотря на некоторые зародыши в архитектуре Древней Греции, с итальянских художников, таких как Джотто в 13 веке; такие правила, как точка схода были впервые сформулированы Брунеллески примерно в 1413 г.,[6] его теория, влияющая на Леонардо и Дюрера. Исаак Ньютон работает над оптический спектр под влиянием Гете с Теория цвета и в свою очередь художники, такие как Филипп Отто Рунге, Дж. М. В. Тернер,[96] то Прерафаэлиты и Василий Кандинский.[97][98] Художники также могут проанализировать симметрия сцены.[99] Инструменты могут применяться математиками, изучающими искусство, или художниками, вдохновленными математикой, такими как М. К. Эшер (вдохновлен Х. С. М. Коксетер ) и архитектор Фрэнк Гери, который более сдержанно утверждал, что системы автоматизированного проектирования позволил ему выразить себя совершенно по-новому.[100]

Художник Ричард Райт утверждает, что математические объекты, которые можно конструировать, можно рассматривать либо «как процессы для моделирования явлений», либо как произведения »компьютерное искусство ". Он рассматривает природу математической мысли, отмечая, что фракталы были известны математикам за столетие до того, как были признаны таковыми. В заключение Райт заявляет, что уместно подвергать математические объекты любым методам, используемым для «примирения с культурными артефактами, такими как искусство, напряжением между объективностью и субъективностью, их метафорическими значениями и характером репрезентативных систем». Он приводит в качестве примера изображение из Набор Мандельброта, изображение, созданное клеточный автомат алгоритм, а компьютерный изображение, и обсуждает, со ссылкой на Тест Тьюринга, ли алгоритмический изделия могут быть арт.[101] Сашо Калайдзиевского Математика и искусство: введение в наглядную математику использует аналогичный подход, рассматривая подходящие темы визуальной математики, такие как мозаики, фракталы и гиперболическая геометрия.[102]
Некоторые из первых произведений компьютерного искусства были созданы Десмонд Пол Генри "Чертежная машина 1", аналоговая машина на основе бомбовый прицел компьютер и выставлен в 1962 году.[103][104] Машина могла создавать сложные, абстрактные, асимметричные, криволинейные, но повторяющиеся линейные рисунки.[103][105] В последнее время, Хамид Надери Еганех создал формы, напоминающие объекты реального мира, такие как рыбы и птицы, используя формулы, которые последовательно меняются, чтобы рисовать семейства кривых или угловых линий.[106][107][108] Такие художники, как Микаэль Хвидтфельдт Кристенсен, создают произведения генеративное или алгоритмическое искусство написав сценарии для программной системы, такой как Структура Synth: художник эффективно направляет систему на применение желаемой комбинации математических операций к выбранному набору данных.[109][110]

Математическая скульптура Вирсавия Гроссман, 2007

Фрактал скульптура: 3D Fraktal 03 / H / dd к Хартмут Скербиш, 2003

Слово Фибоначчи: фрагмент картины Самуэля Монье, 2009 г.

Компьютерное искусство изображение, созданное Десмонд Пол Генри "Чертежная машина 1", экспонируется в 1962 г.

Птица в полете, к Хамид Надери Еганех, 2016, построенный с помощью семейства математических кривых.
От математики к искусству

Математик и физик-теоретик Анри Пуанкаре с Наука и гипотеза был широко прочитан Кубисты, включая Пабло Пикассо и Жан Метцингер.[112][113] Пуанкаре просмотрено Евклидова геометрия как просто одну из многих возможных геометрических конфигураций, а не как абсолютную объективную истину. Возможное существование четвертое измерение вдохновил художников поставить под сомнение классику Перспектива Возрождения: неевклидова геометрия стала реальной альтернативой.[114][115][116] Идея о том, что живопись может быть выражена математически, с помощью цвета и формы, способствовала кубизму, художественному движению, которое привело к абстрактное искусство.[117] Метцингер в 1910 году писал, что: «[Пикассо] излагает свободную, мобильную перспективу, с которой гениальный математик Морис Принст вывел целую геометрию ».[118] Позже Метцингер писал в своих мемуарах:
Морис Принст часто присоединялся к нам ... как художник он концептуализировал математику, как эстетик, которого он привлекал п-мерные континуумы. Он любил интересовать художников новые взгляды на космос что было открыто Шлегель и некоторые другие. Ему это удалось.[119]
Стремление создать учебные или исследовательские модели математических форм естественным образом создает объекты, обладающие симметрией и удивительными или приятными формами. Некоторые из них вдохновили художников, таких как Дадаисты Ман Рэй,[120] Марсель Дюшан[121] и Макс Эрнст,[122][123] и вслед за Ман Рэем Хироши Сугимото.[124]

Ман Рэй сфотографировал некоторые математические модели в Institut Henri Poincaré в Париже, в том числе Objet mathematique (Математический объект). Он отметил, что это представляло Поверхности Эннепера с постоянным отрицательная кривизна, полученный из псевдосфера. Эта математическая основа была для него важна, поскольку позволяла ему отрицать, что объект был «абстрактным», вместо этого заявляя, что он был таким же реальным, как писсуар, который Дюшан превратил в произведение искусства. Ман Рэй признал, что формула объекта [поверхность Эннепера] «ничего не значила для меня, но сами формы были такими же разнообразными и аутентичными, как и любые другие в природе». Он использовал свои фотографии математических моделей в качестве рисунков в своей серии, которую он делал на Шекспир пьесы, такие как его картина 1934 года Антоний и Клеопатра.[125] Репортер Джонатан Китс пишет ForbesLife, утверждает, что Ман Рэй сфотографировал «эллиптические параболоиды и конические точки в том же чувственном свете, что и его фотографии Кики де Монпарнас ", и" гениально перепрофилирует классные математические вычисления, чтобы выявить топологию желания ".[126] Скульпторы двадцатого века, такие как Генри Мур, Барбара Хепворт и Наум Габо черпал вдохновение из математических моделей.[127] Мур писал о своем 1938 году. Струнная мать и дитя: "Несомненно, источником моих струнных фигур был Научный музей ... Я был очарован математическими моделями, которые я там увидел ... Меня волновало не научное изучение этих моделей, а способность смотреть сквозь струны, как в птичьей клетке, и видеть одну форму внутри другой. "[128]

Художники Тео ван Дусбург и Пит Мондриан основал Де Стейл движение, которое они хотели «создать визуальный словарь, состоящий из элементарных геометрических форм, понятных всем и адаптируемых к любой дисциплине».[129][130] Многие из их работ явно состоят из квадратов и треугольников, иногда также с кругами. Художники De Stijl работали в живописи, мебели, дизайне интерьеров и архитектуре.[129] После распада De Stijl Ван Дусбург основал Авангард Арт Конкрет движение, описывающее его 1929–1930 Арифметическая композиция, серия из четырех черных квадратов по диагонали квадратного фона, как «структура, которой можно управлять, определенный поверхность без случайных элементов или индивидуального каприза », но« не лишенная духа, не лишенная универсального и не ... пустая, как есть все который соответствует внутреннему ритму ». Искусствовед Глэдис Фабр отмечает, что в картине работают две прогрессии, а именно растущие черные квадраты и чередующиеся фоны.[131]
Математика мозаика, многогранники, формирование пространства и самореференция предоставили художнику-графику М. К. Эшер (1898–1972) с материалами для гравюры на всю жизнь.[132][133] в Эскиз АльгамбрыЭшер показал, что искусство можно создавать с помощью многоугольников или правильных форм, таких как треугольники, квадраты и шестиугольники. Эшер использовал неправильные многоугольники при мозаике плоскости и часто использовал отражения, скользящие отражения, и переводы для получения дополнительных рисунков. Многие из его работ содержат невозможные конструкции, созданные с использованием геометрических объектов, которые создают противоречие между перспективной проекцией и трехмерностью, но приятны для человеческого зрения. Эшера По возрастанию и по убыванию основан на "невозможная лестница "создан ученым-медиком Лайонел Пенроуз и его сын математик Роджер Пенроуз.[134][135][136]
Некоторые из многочисленных мозаичных рисунков Эшера были вдохновлены разговорами с математиком. Х. С. М. Коксетер на гиперболическая геометрия.[137] Эшера особенно интересовали пять конкретных многогранников, которые много раз встречаются в его работах. В Платоновы тела - тетраэдры, кубы, октаэдры, додекаэдры и икосаэдры - особенно выделяются в Порядок и хаос и Четыре обычных твердых тела.[138] Эти звездчатые фигуры часто находятся внутри другой фигуры, что еще больше искажает угол обзора и форму многогранников и обеспечивает многогранное перспективное произведение искусства.[139]
Визуальная сложность математических структур, таких как мозаика и многогранники, вдохновила на создание множества математических произведений. Стюарт Гроб делает многогранные пазлы в редких и красивых лесах; Джордж У. Харт работает по теории многогранники и лепит предметы, вдохновленные ими; Магнус Веннингер делает «особо красивые» модели из сложные звездчатые многогранники.[140]
Искаженные перспективы анаморфоз исследовались в искусстве с шестнадцатого века, когда Ганс Гольбейн Младший включил сильно искаженный череп в свою картину 1533 года Послы. С тех пор многие художники, в том числе Эшер, прибегли к анаморфным трюкам.[141]
Математика топология вдохновил нескольких художников современности. Скульптор Джон Робинсон (1935–2007) создал такие произведения, как Гордиев узел и Группы Дружбы, отображение теория узлов из полированной бронзы.[7] Другие работы Робинсона исследуют топологию торы. Бытие основан на Кольца Борромео - набор из трех кругов, два из которых не связаны, но в которых всю конструкцию нельзя разобрать без разрушения.[142] Скульптор Геламан Фергюсон создает сложные поверхности и другие топологические объекты.[143] Его работы представляют собой визуальные представления математических объектов; Восьмеричный путь основан на проективная специальная линейная группа PSL (2,7), конечная группа из 168 элементов.[144][145] Скульптор Вирсавия Гроссман аналогично основывает свою работу на математических структурах.[146][147]
Исследовательский проект гуманитарных наук исследует связи между математикой и искусством через Лента Мебиуса, флексагоны, оригами и панорама фотография.[148]
Математические объекты, включая Многообразие Лоренца и гиперболическая плоскость были созданы с использованием волокна искусства в том числе крючком.[d][150] Американский ткачиха Ада Дитц написал монографию 1949 г. Алгебраические выражения в тканях ручной работы, определяя образцы ткачества на основе расширения многомерного многочлены.[151] Математик Дайна Тайминя продемонстрировал особенности гиперболической плоскости крючком в 2001 году.[152] Это привело Маргарет и Кристин Вертхайм связать крючком коралловый риф, состоящий из многих морских животных, таких как голожаберники формы которых основаны на гиперболических плоскостях.[153] Математик Дж. С. П. Миллер использовал Правило 90 клеточный автомат разрабатывать гобелены с изображением как деревьев, так и абстрактных узоров из треугольников.[154] "Математики"[155] Пэт Эшфорт и Стив Пламмер используют связанные версии математических объектов, таких как гексафлексагоны в их обучении, хотя их Губка менгера вязать оказалось слишком сложно, и вместо этого он был сделан из пластикового полотна.[156][157] Представлен их проект "mathghans" (афганцы для школ). Вязание в британский курс математики и технологий.[158][159]

Четырехмерное пространство к Кубизм: Esprit Jouffret 1903 год Traité élémentaire de géométrie à quatre sizes.[160][e]

Де Стейл: Тео ван Дусбург геометрический Композиция I (Натюрморт), 1916

Педагогика к искусству: Магнус Веннингер с некоторыми из его звездчатые многогранники, 2009

А Лента Мебиуса шарф в вязание крючком, 2007

Анаморфизм: Послы к Ганс Гольбейн Младший, 1533 г., с сильно искаженным черепом на переднем плане
Связанные крючком коралловый риф: многие животные смоделированы как гиперболические плоскости с варьируемыми параметрами на Маргарет и Кристин Вертхайм. Föhr Reef, Тюбинген, 2013 г.

Иллюстрирование математики


Моделирование - далеко не единственный способ проиллюстрировать математические концепции. Джотто Стефанески Триптих, 1320, иллюстрирует рекурсия в виде mise en abyme; на центральной панели триптиха внизу слева изображена коленопреклоненная фигура кардинала Стефанески, держащего триптих в качестве подношения.[162] Джорджио Кирико с метафизический картины, такие как его 1917 Великий метафизический интерьер изучить вопрос об уровнях репрезентации в искусстве, изображая картины в его картинах.[163]
Искусство может служить примером логических парадоксов, как в некоторых картинах сюрреалист Рене Магритт, который можно читать как семиотический анекдоты про путаницу между уровнями. В La Condition Humaine (1933) Магритт изображает мольберт (на реальном холсте), органично поддерживающий вид через окно, обрамленное «настоящими» занавесками на картине. Точно так же Эшер Галерея печати (1956 г.) - гравюра, изображающая искаженный город с галереей, рекурсивно содержит изображение, и поэтому до бесконечности.[164] Магритт использовал сферы и кубоиды, чтобы по-другому искажать реальность, раскрашивая их рядом с домами в своем 1931 году. Счет в уме как если бы они были детскими строительными блоками, но размером с дом.[165] Хранитель заметил, что "жуткий образ игрушечного городка" предсказывал Модернизм узурпация "уютных традиционных форм", но также играет на человеческой склонности искать закономерности в природе.[166]

Последняя картина Сальвадора Дали, Ласточкин хвост (1983), был частью серии, вдохновленной Рене Том с теория катастроф.[168] Испанский художник и скульптор Пабло Паласуэло (1916–2007) сосредоточился на исследовании формы. He developed a style that he described as the geometry of life and the geometry of all nature. Consisting of simple geometric shapes with detailed patterning and coloring, in works such as Angular I и Automnes, Palazuelo expressed himself in geometric transformations.[7]
The artist Adrian Gray practises балансировка камня, exploiting трение и центр тяжести to create striking and seemingly impossible compositions.[169]

Artists, however, do not necessarily take geometry literally. В качестве Дуглас Хофштадтер writes in his 1980 reflection on human thought, Гедель, Эшер, Бах, by way of (among other things) the mathematics of art: "The difference between an Escher drawing and неевклидова геометрия is that in the latter, comprehensible interpretations can be found for the undefined terms, resulting in a comprehensible total system, whereas for the former, the end result is not reconcilable with one's conception of the world, no matter how long one stares at the pictures." Hofstadter discusses the seemingly парадоксальный литография Галерея печати by M. C. Escher; it depicts a seaside town containing an art gallery which seems to contain a painting of the seaside town, there being a "strange loop, or tangled hierarchy" to the levels of reality in the image. The artist himself, Hofstadter observes, is not seen; his reality and his relation to the lithograph are not paradoxical.[167] The image's central void has also attracted the interest of mathematicians Bart de Smit and Хендрик Ленстра, who propose that it could contain a Эффект Дросте copy of itself, rotated and shrunk; this would be a further illustration of recursion beyond that noted by Hofstadter.[170][171]
Analysis of art history
Algorithmic analysis of images of artworks, for example using X-ray fluorescence spectroscopy, can reveal information about art. Such techniques can uncover images in layers of paint later covered over by an artist; help art historians to visualize an artwork before it cracked or faded; help to tell a copy from an original, or distinguish the brushstroke style of a master from those of his apprentices.[172][173]

Джексон Поллок с drip painting стиль[174] has a definite фрактальная размерность;[175] among the artists who may have influenced Pollock's controlled хаос,[176] Max Ernst painted Фигуры Лиссажу directly by swinging a punctured bucket of paint over a canvas.[177]
Компьютерный ученый Neil Dodgson investigated whether Бриджит Райли 's stripe paintings could be characterised mathematically, concluding that while separation distance could "provide some characterisation" and global энтропия worked on some paintings, автокорреляция failed as Riley's patterns were irregular. Local entropy worked best, and correlated well with the description given by the art critic Robert Kudielka.[178]
The American mathematician Джордж Биркофф 's 1933 Эстетическая мера proposes a quantitative metric of the aesthetic quality of an artwork. It does not attempt to measure the connotations of a work, such as what a painting might mean, but is limited to the "elements of order" of a polygonal figure. Birkhoff first combines (as a sum) five such elements: whether there is a vertical axis of symmetry; whether there is optical equilibrium; how many rotational symmetries it has; how wallpaper-like the figure is; and whether there are unsatisfactory features such as having two vertices too close together. This metric, О, takes a value between −3 and 7. The second metric, C, counts elements of the figure, which for a polygon is the number of different straight lines containing at least one of its sides. Birkhoff then defines his aesthetic measure of an object's beauty as O/C. This can be interpreted as a balance between the pleasure looking at the object gives, and the amount of effort needed to take it in. Birkhoff's proposal has been criticized in various ways, not least for trying to put beauty in a formula, but he never claimed to have done that.[179]
Stimuli to mathematical research
Art has sometimes stimulated the development of mathematics, as when Brunelleschi's theory of perspective in architecture and painting started a cycle of research that led to the work of Брук Тейлор и Иоганн Генрих Ламберт on the mathematical foundations of perspective drawing,[180] and ultimately to the mathematics of проективная геометрия из Girard Desargues и Жан-Виктор Понселе.[181]
The Japanese paper-folding art of оригами has been reworked mathematically by Tomoko Fusé using modules, congruent pieces of paper such as squares, and making them into polyhedra or tilings.[182] Paper-folding was used in 1893 by T. Sundara Rao in his Geometric Exercises in Paper Folding to demonstrate geometrical proofs.[183] В математика складывания бумаги был исследован в Maekawa's theorem,[184] Kawasaki's theorem,[185] и Huzita–Hatori axioms.[186]

Stimulus to проективная геометрия: Альберти 's diagram showing a circle seen in perspective as an эллипс. Della Pittura, 1435–6
Illusion to Op art

Оптические иллюзии такой как Спираль Фрейзера strikingly demonstrate limitations in human visual perception, creating what the историк искусства Эрнст Гомбрих called a "baffling trick." The black and white ropes that appear to form спирали на самом деле концентрические круги. The mid-twentieth century Op art or optical art style of painting and graphics exploited such effects to create the impression of movement and flashing or vibrating patterns seen in the work of artists such as Бриджит Райли, Spyros Horemis,[188] и Виктор Вазарели.[189]
Сакральная геометрия
A strand of art from Ancient Greece onwards sees God as the geometer of the world, and the world's geometry therefore as sacred. The belief that God created the universe according to a geometric plan has ancient origins. Плутарх attributed the belief to Платон, writing that "Plato said God geometrizes continually" (Convivialium disputationum, liber 8,2). This image has influenced Western thought ever since. The Platonic concept derived in its turn from a Пифагорейский notion of harmony in music, where the notes were spaced in perfect proportions, corresponding to the lengths of the lyre's strings; indeed, the Pythagoreans held that everything was arranged by Number. In the same way, in Platonic thought, the regular or Platonic solids dictate the proportions found in nature, and in art.[190][191] An illumination in the 13th-century Codex Vindobonensis shows God drawing out the universe with a pair of compasses, which may refer to a verse in the Old Testament: "When he established the heavens I was there: when he set a compass upon the face of the deep" (Proverbs 8:27), .[192] In 1596, the mathematical astronomer Иоганн Кеплер modelled the universe as a set of nested Platonic solids, determining the relative sizes of the orbits of the planets.[192] Уильям Блейк с Древний Днями (изображающий Уризен, Blake's embodiment of reason and law) and his painting of the physicist Исаак Ньютон, naked, hunched and drawing with a compass, use the symbolism of compasses to critique conventional reason and materialism as narrow-minded.[193][194]Сальвадор Дали 1954 год Распятие (Corpus Hypercubus) depicts the cross as a гиперкуб, representing the divine perspective with four dimensions rather than the usual three.[79] In Dali's Таинство Тайной вечери (1955) Christ and his disciples are pictured inside a giant додекаэдр.[195]

God the geometer. Codex Vindobonensis, c. 1220

The creation, with the Пантократор bearing . Библия Святого Луи, c. 1220–40
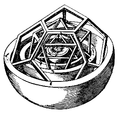
Иоганн Кеплер с Платоново твердое тело model of planetary spacing in the Солнечная система из Mysterium Cosmographicum, 1596

Уильям Блейк с Ветхий днями, 1794

Уильяма Блейка Ньютон, c. 1800
Смотрите также
Примечания
- ^ In Piero's Italian: "una cosa tanto picholina quanto e possible ad ochio comprendere".
- ^ The ratio of the slant height to half the base length is 1.619, less than 1% from the golden ratio, implying use of Kepler's triangle (face angle 51°49').[43][44] It is more likely that pyramids were made with the 3-4-5 triangle (face angle 53°8'), known from the Математический папирус Райнда; or with the triangle with base to hypotenuse ratio 1:4/π (face angle 51°50').[45]
- ^ 'Пластик ' named the ability to take on a chosen three-dimensional shape.
- ^ Images and videos of Хинке Осинга 's crocheted Lorenz manifold reached international television news, as can be seen in the linked website.[149]
- ^ Морис Принст gave a copy to Пабло Пикассо, whose sketchbooks for Les Demoiselles d'Avignon illustrate Jouffret's influence.[112][161]
Рекомендации
- ^ а б c d Ziegler, Günter M. (3 December 2014). "Многогранник Дюрера: 5 теорий, объясняющих сумасшедший куб Меленколии". Хранитель. Получено 27 октября 2015.
- ^ а б Коломбо, К .; Del Bimbo, A.; Pernici, F. (2005). "Metric 3D reconstruction and texture acquisition of surfaces of revolution from a single uncalibrated view". IEEE Transactions по анализу шаблонов и машинному анализу. 27 (1): 99–114. CiteSeerX 10.1.1.58.8477. Дои:10.1109/TPAMI.2005.14. PMID 15628272. S2CID 13387519.
- ^ а б Stewart, Andrew (November 1978). "Polykleitos of Argos," One Hundred Greek Sculptors: Their Careers and Extant Works". Журнал эллинских исследований. 98: 122–131. Дои:10.2307/630196. JSTOR 630196.
- ^ а б Tobin, Richard (October 1975). "The Canon of Polykleitos". Американский журнал археологии. 79 (4): 307–321. Дои:10.2307/503064. JSTOR 503064.
- ^ Raven, J. E. (1951). "Polyclitus and Pythagoreanism". Классический квартал. 1 (3–4): 147–. Дои:10.1017/s0009838800004122.
- ^ а б c О'Коннор, Дж. Дж .; Robertson, E. F. (January 2003). "Mathematics and art – perspective". Сент-Эндрюсский университет. Получено 1 сентября 2015.
- ^ а б c d Emmer, Michelle, ed. (2005). The Visual Mind II. MIT Press. ISBN 978-0-262-05048-7.
- ^ Вазари, Джорджио (1550). Жития художников. Torrentino. п. Chapter on Brunelleschi.
- ^ Alberti, Leon Battista; Spencer, John R. (1956) [1435]. On Painting. Издательство Йельского университета.
- ^ Field, J. V. (1997). The Invention of Infinity: Mathematics and Art in the Renaissance. Издательство Оксфордского университета. ISBN 978-0-19-852394-9.
- ^ Witcombe, Christopher L. C. E. "Art History Resources". Получено 5 сентября 2015.
- ^ а б c d е Харт, Джордж У. "Polyhedra in Art". Получено 24 июн 2015.
- ^ Каннингем, Лоуренс; Reich, John; Fichner-Rathus, Lois (1 January 2014). Культура и ценности: обзор западных гуманитарных наук. Cengage Learning. п. 375. ISBN 978-1-285-44932-6.
which illustrate Uccello's fascination with perspective. The jousting combatants engage on a battlefield littered with broken lances that have fallen in a near-grid pattern and are aimed toward a vanishing point somewhere in the distance.
- ^ della Francesca, Piero (1942) [c. 1474]. G. Nicco Fasola (ed.). De prospectiva pingendi. Florence.
- ^ della Francesca, Piero (1970) [Fifteenth century]. G. Arrighi (ed.). Trattato d'Abaco. Пиза.
- ^ della Francesca, Piero (1916). G. Mancini (ed.). Опера "De corporibus regularibus" Пьетро Франчески, детто делла Франческа узурпата да фра Лука Пачоли.
- ^ Vasari, G. (1878). G. Milanesi (ed.). Le Opere, volume 2. п. 490.
- ^ Дзуффи, Стефано (1991). Пьеро делла Франческа. L'Unità – Mondadori Arte. п.53.
- ^ Хит, Т. (1908). Тринадцать книг стихий Евклида. Издательство Кембриджского университета. п.97.
- ^ Grendler, P. (1995). M.A. Lavin (ed.). What Piero Learned in School: Fifteenth-Century Vernacular Education. Piero della Francesca and His Legacy. Университетское издательство Новой Англии. С. 161–176.
- ^ Alberti, Leon Battista; Grayson, Cecil (trans.) (1991). Kemp, Martin (ed.). On Painting. Пингвин Классика.
- ^ Петерсон, Марк. "The Geometry of Piero della Francesca".
In Book I, after some elementary constructions to introduce the idea of the apparent size of an object being actually its angle subtended at the eye, and referring to Euclid's Elements Books I and VI, and Euclid's Optics, he turns, in Proposition 13, to the representation of a square lying flat on the ground in front of the viewer. What should the artist actually draw? After this, objects are constructed in the square (tilings, for example, to represent a tiled floor), and corresponding objects are constructed in perspective; in Book II prisms are erected over these planar objects, to represent houses, columns, etc.; but the basis of the method is the original square, from which everything else follows.
- ^ Hockney, David (2006). Тайные знания: открытие утерянных техник старых мастеров. Темза и Гудзон. ISBN 978-0-500-28638-8.
- ^ Van Riper, Frank. "Hockney's 'Lucid' Bomb At the Art Establishment". Вашингтон Пост. Получено 4 сентября 2015.
- ^ Marr, Andrew (7 October 2001). "What the eye didn't see". Хранитель. Получено 4 сентября 2015.
- ^ Janson, Jonathan (25 April 2003). "An Interview with Philip Steadman". Essential Vermeer. Получено 5 сентября 2015.
- ^ Steadman, Philip (2002). Vermeer's Camera: Uncovering the Truth Behind the Masterpieces. Оксфорд. ISBN 978-0-19-280302-3.
- ^ Харт, Джордж. "Luca Pacioli's Polyhedra". Получено 13 августа 2009.
- ^ Morris, Roderick Conway (27 January 2006). "Palmezzano's Renaissance:From shadows, painter emerges". Нью-Йорк Таймс. Получено 22 июля 2015.
- ^ Calter, Paul. "Geometry and Art Unit 1". Дартмутский колледж. Получено 13 августа 2009.
- ^ Brizio, Anna Maria (1980). Leonardo the Artist. Макгроу-Хилл.
- ^ Ladwein, Michael (2006). Leonardo Da Vinci, the Last Supper: A Cosmic Drama and an Act of Redemption. Издательство Temple Lodge. С. 61–62. ISBN 978-1-902636-75-7.
- ^ Turner, Richard A. (1992). Inventing Leonardo. Альфред А. Кнопф.
- ^ Wolchover, Natalie (31 January 2012). "Did Leonardo da Vinci copy his famous 'Vitruvian Man'?". Новости NBC. Получено 27 октября 2015.
- ^ Criminisi, A .; Kempz, M.; Kang, S. B. (2004). "Reflections of Reality in Jan van Eyck and Robert Campin" (PDF). Исторические методы. 37 (3): 109–121. Дои:10.3200/hmts.37.3.109-122. S2CID 14289312.
- ^ Cucker, Felix (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. pp. 299–300, 306–307. ISBN 978-0-521-72876-8.
- ^ Cucker, Felix (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. С. 269–278. ISBN 978-0-521-72876-8.
- ^ Joyce, David E. (1996). "Euclid's Elements, Book II, Proposition 11". Университет Кларка. Получено 24 сентября 2015.
- ^ Seghers, M. J.; Longacre, J. J.; Destefano, G. A. (1964). "The Golden Proportion and Beauty". Пластическая и реконструктивная хирургия. 34 (4): 382–386. Дои:10.1097/00006534-196410000-00007. S2CID 70643014.
- ^ Mainzer, Klaus (1996). Симметрии природы: Справочник по философии природы и науки. Вальтер де Грюйтер. п. 118.
- ^ "Mathematical properties in ancient theatres and amphitheatres". Архивировано из оригинал 15 июля 2017 г.. Получено 29 января 2014.
- ^ "Architecture: Ellipse?". The-Colosseum.net. Получено 29 января 2014.
- ^ а б c d Марковский, Джордж (январь 1992 г.). «Заблуждения о золотом сечении» (PDF). The College Mathematics Journal. 23 (1): 2–19. Дои:10.2307/2686193. JSTOR 2686193. Архивировано из оригинал (PDF) на 2008-04-08. Получено 2015-06-26.
- ^ Taseos, Socrates G. (1990). Back in Time 3104 B.C. to the Great Pyramid. SOC Publishers.
- ^ Gazale, Midhat (1999). Гномон: от фараонов до фракталов. European Journal of Physics. 20. Издательство Принстонского университета. п. 523. Bibcode:1999EJPh...20..523G. Дои:10.1088/0143-0807/20/6/501. ISBN 978-0-691-00514-0.
- ^ Huntley, H.E. (1970). The Divine Proportion. Дувр.
- ^ Хеменуэй, Прия (2005). Divine Proportion: Phi In Art, Nature, and Science. Стерлинг. п. 96.
- ^ Usvat, Liliana. "Mathematics of the Parthenon". Математический журнал. Получено 24 июн 2015.
- ^ Boussora, Kenza; Mazouz, Said (Spring 2004). "The Use of the Golden Section in the Great Mosque of Kairouan". Сетевой журнал Nexus. 6 (1): 7–16. Дои:10.1007/s00004-004-0002-y.
The geometric technique of construction of the golden section seems to have determined the major decisions of the spatial organisation. The golden section appears repeatedly in some part of the building measurements. It is found in the overall proportion of the plan and in the dimensioning of the prayer space, the court and the minaret. The existence of the golden section in some parts of Kairouan mosque indicates that the elements designed and generated with this principle may have been realised at the same period.
- ^ Brinkworth, Peter; Scott, Paul (2001). "The Place of Mathematics". Учитель математики Австралии. 57 (3): 2.
- ^ Chanfón Olmos, Carlos (1991). Curso sobre Proporción. Procedimientos reguladors en construcción. Convenio de intercambio Unam–Uady. México – Mérica.
- ^ Ливио, Марио (2002). "The Golden Ratio: The Story of Phi, The World's Most Astonishing Number". The Golden Ratio : The Story of Phi. Bibcode:2002grsp.book.....L.
- ^ Smith, Norman A. F. (2001). "Cathedral Studies: Engineering or History" (PDF). Сделки Общества Ньюкоменов. 73: 95–137. Дои:10.1179/tns.2001.005. S2CID 110300481. Архивировано из оригинал (PDF) на 2015-12-11.
- ^ McVeigh, Karen (28 December 2009). "Why golden ratio pleases the eye: US academic says he knows art secret". Хранитель. Получено 27 октября 2015.
- ^ Aarts, J.; Fokkink, R.; Kruijtzer, G. (2001). "Morphic numbers" (PDF). Nieuw Arch. Wiskd. 5. 2 (1): 56–58.
- ^ а б Padovan, Richard (2002). Уильямс, Ким; Francisco Rodrigues, Jose (eds.). "Dom Hans Van Der Laan And The Plastic Number". Nexus IV: архитектура и математика: 181–193.
- ^ а б c d Salingaros, Nikos (November 1996). "The 'life' of a carpet: an application of the Alexander rules". 8th International Conference on Oriental Carpets. Перепечатано в Eiland, M.; Pinner, M., eds. (1998). Oriental Carpet and Textile Studies V. Danville, CA: Conference on Oriental Carpets.
- ^ а б c Cucker, Felix (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. С. 89–102. ISBN 978-0-521-72876-8.
- ^ а б Лернер, Мартин (1984). The flame and the lotus : Indian and Southeast Asian art from the Kronos collections (Каталог выставки под ред.). Метрополитен-музей.
- ^ а б Ellison, Elaine; Venters, Diana (1999). Mathematical Quilts: No Sewing Required. Key Curriculum.
- ^ а б Castera, Jean Marc; Peuriot, Francoise (1999). Arabesques. Decorative Art in Morocco. Art Creation Realisation. ISBN 978-2-86770-124-5.
- ^ Cucker, Felix (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. С. 103–106. ISBN 978-0-521-72876-8.
- ^ Dye, Daniel S. (1974). Chinese Lattice Designs. Дувр. стр.30–39.
- ^ belcastro, sarah-marie (2013). "Adventures in Mathematical Knitting". Американский ученый. 101 (2): 124. Дои:10.1511/2013.101.124.
- ^ Taimina, Daina (2009). Связанные крючком приключения с гиперболическими плоскостями. А. К. Питерс. ISBN 978-1-56881-452-0.
- ^ Snook, Barbara. Florentine Embroidery. Scribner, Second edition 1967.
- ^ Williams, Elsa S. Bargello: Florentine Canvas Work. Van Nostrand Reinhold, 1967.
- ^ Грюнбаум, Бранко; Shephard, Geoffrey C. (May 1980). "Satins and Twills: An Introduction to the Geometry of Fabrics". Математический журнал. 53 (3): 139–161. Дои:10.2307/2690105. HDL:10338.dmlcz/104026. JSTOR 2690105.
- ^ а б Гэмвелл, Линн (2015). Математика и искусство: история культуры. Издательство Принстонского университета. п. 423. ISBN 978-0-691-16528-8.
- ^ Бейкер, Патрисия Л .; Смит, Хилари (2009). Иран (3-е изд.). Путеводители Брэдта. п. 107. ISBN 978-1-84162-289-7.
- ^ Irvine, Veronika; Ruskey, Frank (2014). "Developing a Mathematical Model for Bobbin Lace". Журнал математики и искусств. 8 (3–4): 95–110. arXiv:1406.1532. Bibcode:2014arXiv1406.1532I. Дои:10.1080/17513472.2014.982938. S2CID 119168759.
- ^ Лу, Питер Дж .; Стейнхардт, Пол Дж. (2007). «Десятиугольные и квазикристаллические плитки в средневековой исламской архитектуре». Наука. 315 (5815): 1106–1110. Bibcode:2007Научный ... 315.1106Л. Дои:10.1126 / science.1135491. PMID 17322056. S2CID 10374218.
- ^ van den Hoeven, Saskia; van der Veen, Maartje. "Muqarnas-Mathematics in Islamic Arts" (PDF). Архивировано из оригинал (PDF) 27 сентября 2013 г.. Получено 15 января 2016.
- ^ Markowsky, George (March 2005). "Рецензия на книгу: Золотое сечение" (PDF). Уведомления Американского математического общества. 52 (3): 344–347.
- ^ Panofsky, E. (1955). The Life and Art of Albrecht Durer. Принстон.
- ^ Харт, Джордж У. "Dürer's Polyhedra". Получено 13 августа 2009.
- ^ Dürer, Albrecht (1528). Hierinn sind begriffen vier Bucher von menschlicher Proportion. Nurenberg. Получено 24 июн 2015.
- ^ а б Rudy Rucker, Четвертое измерение: к геометрии высшей реальности, Courier Corporation, 2014, ISBN 0486798194
- ^ а б c "Crucifixion (Corpus Hypercubus)". Метрополитен-музей. Получено 5 сентября 2015.
- ^ Schreiber, P. (1999). "A New Hypothesis on Durer's Enigmatic Polyhedron in His Copper Engraving 'Melencolia I'". Historia Mathematica. 26 (4): 369–377. Дои:10.1006 / hmat.1999.2245.
- ^ Dodgson, Campbell (1926). Альбрехт Дюрер. London: Medici Society. п. 94.
- ^ Schuster, Peter-Klaus (1991). Melencolia I: Dürers Denkbild. Берлин: Gebr. Манн Верлаг. pp. 17–83.
- ^ Панофски, Эрвин; Klibansky, Raymond; Saxl, Fritz (1964). Saturn and melancholy. Основные книги.
- ^ Lukman, Muhamad; Hariadi, Yun; Destiarmand, Achmad Haldani (2007). "Batik Fractal : Traditional Art to Modern Complexity". Proceeding Generative Art X, Milan, Italy.
- ^ Ouellette, Jennifer (November 2001). "Pollock's Fractals". Откройте для себя журнал. Получено 26 сентября 2016.
- ^ Галилей, Галилей (1623). Пробирщик., as translated in Drake, Stillman (1957). Открытия и мнения Галилея. Doubleday. стр.237–238. ISBN 978-0-385-09239-5.
- ^ Cucker, Felix (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. п. 381. ISBN 978-0-521-72876-8.
- ^ Cucker, Felix (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. п. 10. ISBN 978-0-521-72876-8.
- ^ King, Jerry P. (1992). The Art of Mathematics. Fawcett Columbine. С. 8–9. ISBN 978-0-449-90835-8.
- ^ King, Jerry P. (1992). The Art of Mathematics. Fawcett Columbine. С. 135–139. ISBN 978-0-449-90835-8.
- ^ Devlin, Keith (2000). "Do Mathematicians Have Different Brains?". The Math Gene: How Mathematical Thinking Evolved And Why Numbers Are Like Gossip. Основные книги. п. 140. ISBN 978-0-465-01619-8.
- ^ Wasilewska, Katarzyna (2012). "Mathematics in the World of Dance" (PDF). Мосты. Получено 1 сентября 2015.
- ^ а б Малькевич, Иосиф. «Математика и искусство». Американское математическое общество. Получено 1 сентября 2015.
- ^ Малькевич, Иосиф. «Математика и искусство. 2. Математические инструменты для художников». Американское математическое общество. Получено 1 сентября 2015.
- ^ «Математика и искусство: хорошее, плохое и красивое». Математическая ассоциация Америки. Получено 2 сентября 2015.
- ^ Коэн, Луиза (1 июля 2014 г.). «Как вращать цветовое колесо, Тернер, Малевич и другие». Галерея Тейт. Получено 4 сентября 2015. Цитировать журнал требует
| журнал =(помощь) - ^ Кемп, Мартин (1992). Наука об искусстве: оптические темы в западном искусстве от Брунеллески до Сёра. Издательство Йельского университета. ISBN 978-968-867-185-6.
- ^ Гейдж, Джон (1999). Цвет и культура: практика и значение от античности до абстракции. Калифорнийский университет Press. п. 207. ISBN 978-0-520-22225-0.
- ^ Малькевич, Иосиф. «Математика и искусство. 3. Симметрия». Американское математическое общество. Получено 1 сентября 2015.
- ^ Малькевич, Иосиф. «Математика и искусство. 4. Художники-математики и художники-математики». Американское математическое общество. Получено 1 сентября 2015.
- ^ Райт, Ричард (1988). «Некоторые вопросы развития компьютерного искусства как математического вида искусства». Леонардо. 1 (Electronic Art, дополнительный выпуск): 103–110. Дои:10.2307/1557919. JSTOR 1557919.
- ^ Калайдзиевский, Сашо (2008). Математика и искусство: введение в наглядную математику. Чепмен и Холл. ISBN 978-1-58488-913-7.
- ^ а б Беддард, Хонор (2011-05-26). "Компьютерное искусство в V&A". Музей Виктории и Альберта. Получено 22 сентября 2015.
- ^ «Компьютер делает рисунки: тысячи линий в каждом». Хранитель. 17 сентября 1962 г. в Беддарде, 2015.
- ^ О'Ханрахан, Элейн (2005). Машины для рисования: машина создавала рисунки доктора Д. П. Генри в связи с концептуальными и технологическими разработками в искусстве, созданном машинами (Великобритания, 1960–1968). Неопубликованный MPhil. Тезис. Университет Джона Мура, Ливерпуль. в Беддарде, 2015.
- ^ Беллос, Алекс (24 февраля 2015 г.). «Улов дня: математик ловит странную, сложную рыбу». Хранитель. Получено 25 сентября 2015.
- ^ ""Птица в полете (2016), "Хамид Надери Еганех". Американское математическое общество. 23 марта 2016 г.. Получено 6 апреля, 2017.
- ^ Чанг, Стефи (18 сентября 2015 г.). «Следующий да Винчи? Гений математики, использующий формулы для создания фантастических произведений искусства». CNN.
- ^ Левин, Голаны (2013). "Генеративные художники". CMUEMS. Получено 27 октября 2015. Это включает ссылку на Hvidtfeldts Syntopia.
- ^ Веростко Роман. «Алгористы». Получено 27 октября 2015.
- ^ Кукер, Феликс (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. С. 315–317. ISBN 978-0-521-72876-8.
- ^ а б Миллер, Артур I. (2001). Эйнштейн, Пикассо: пространство, время и красота, порождающая хаос. Нью-Йорк: Основные книги. п.171. ISBN 978-0-465-01860-4.
- ^ Миллер, Артур I. (2012). Insights of Genius: образность и творчество в науке и искусстве. Springer. ISBN 978-1-4612-2388-7.
- ^ Хендерсон, Линда Дэлримпл (1983). Четвертое измерение и неевклидова геометрия в современном искусстве. Издательство Принстонского университета.
- ^ Антлифф, Марк; Leighten, Патрисия Ди (2001). Кубизм и культура (PDF). Темза и Гудзон.[постоянная мертвая ссылка ]
- ^ Эверделл, Уильям Р. (1997). Первые современные люди: профили в истоках мысли XX века. Издательство Чикагского университета. п.312. ISBN 978-0-226-22480-0.
- ^ Грин, Кристофер (1987). Кубизм и его враги, современные движения и реакция во французском искусстве 1916–1928 гг.. Издательство Йельского университета. С. 13–47.
- ^ Метцингер, Жан (Октябрь – ноябрь 1910 г.). "Note sur la peinture". Сковорода: 60. в Миллер (2001). Эйнштейн, Пикассо. Основные книги. п.167.
- ^ Метцингер, Жан (1972). Le Cubisme était né. Éditions Présence. С. 43–44. в Ферри, Люк (1993). Homo Aestheticus: изобретение вкуса в эпоху демократии. Роберт Де Лоаиза, пер. Издательство Чикагского университета. п.215. ISBN 978-0-226-24459-4.
- ^ «Уравнения Ман Рэя – человека. Путешествие от математики к Шекспиру. 7 февраля - 10 мая 2015 г.». Коллекция Филлипса. Получено 5 сентября 2015.
- ^ Адкок, Крейг (1987). «Эротизм Дюшана: математический анализ». Iowa Research Online. 16 (1): 149–167.
- ^ Старейшина, Р. Брюс (2013). ДАДА, сюрреализм и кинематографический эффект. Издательство Университета Уилфрида Лорье. п. 602. ISBN 978-1-55458-641-7.
- ^ Таббс, Роберт (2014). Математика в литературе и искусстве ХХ века: содержание, форма, смысл. JHU Press. п. 118. ISBN 978-1-4214-1402-7.
- ^ «Концептуальные формы и математические модели Хироши Сугимото, 7 февраля - 10 мая 2015 г.». Коллекция Филлипса. Получено 5 сентября 2015.
- ^ Таббс, Роберт (2014). Математика в литературе и искусстве ХХ века. Джона Хопкинса. С. 8–10. ISBN 978-1-4214-1380-8.
- ^ Китс, Джонатон (13 февраля 2015 г.). «Посмотрите, как Ман Рэй сделал эллиптические параболоиды эротическими на этой выставке фотографий из коллекции Филлипса». Forbes. Получено 10 сентября 2015.
- ^ Гэмвелл, Линн (2015). Математика и искусство: история культуры. Издательство Принстонского университета. С. 311–312. ISBN 978-0-691-16528-8.
- ^ Hedgecoe, Джон, изд. (1968). Генри Мур: текст на его скульптуре. Генри Спенсер Мур. Саймон и Шустер. п. 105.
- ^ а б "Де Стейл". Глоссарий Тейт. Тейт. Получено 11 сентября 2015.
- ^ Curl, Джеймс Стивенс (2006). Словарь архитектуры и ландшафтной архитектуры (Второе изд.). Издательство Оксфордского университета. ISBN 978-0-19-860678-9.
- ^ Таббс, Роберт (2014). Математика в литературе и искусстве ХХ века: содержание, форма, смысл. JHU Press. С. 44–47. ISBN 978-1-4214-1402-7.
- ^ "Экскурсия: М.С. Эшер - жизнь и творчество". NGA. Архивировано из оригинал 3 августа 2009 г.. Получено 13 августа 2009.
- ^ "МС Эшер". Mathacademy.com. 1 ноября 2007 г.. Получено 13 августа 2009.
- ^ Penrose, L.S .; Пенроуз Р. (1958). «Невозможные объекты: особый вид визуальной иллюзии». Британский журнал психологии. 49 (1): 31–33. Дои:10.1111 / j.2044-8295.1958.tb00634.x. PMID 13536303.
- ^ Kirousis, Lefteris M .; Пападимитриу, Христос Х. (1985). Сложность распознавания многогранных сцен. 26-й ежегодный симпозиум по основам компьютерных наук (FOCS 1985). С. 175–185. CiteSeerX 10.1.1.100.4844. Дои:10.1109 / sfcs.1985.59. ISBN 978-0-8186-0644-1.
- ^ Купер, Мартин (2008). «Сговорчивость к интерпретации рисунков». Интерпретация рисования линий. Springer-Verlag. стр.217 –230. Дои:10.1007/978-1-84800-229-6_9. ISBN 978-1-84800-229-6.
- ^ Робертс, Шивон (2006). "Кокстеринг" с М.К. Эшер. Король бесконечного пространства: Дональд Кокстер, человек, спасший геометрию. Уокер. п. Глава 11.
- ^ Эшер, М. (1988). Мир MC Эшера. Случайный дом.
- ^ Escher, M.C .; Vermeulen, M.W .; Форд, К. (1989). Эшер о Эшере: исследование бесконечности. HN Abrams.
- ^ Малькевич, Иосиф. «Математика и искусство. 5. Многогранники, мозаики и разрезы». Американское математическое общество. Получено 1 сентября 2015.
- ^ Марколли, Матильда (Июль 2016 г.). Понятие пространства в математике через призму современного искусства (PDF). Книги века. С. 23–26.
- ^ "Джон Робинсон". Фонд Брэдшоу. 2007 г.. Получено 13 августа 2009.
- ^ "Веб-сайт Геламана Фергюсона". Helasculpt.com. Архивировано из оригинал 11 апреля 2009 г.. Получено 13 августа 2009.
- ^ Терстон, Уильям П. (1999). Леви, Сильвио (ред.). Восьмеричный путь: математическая скульптура Геламана Фергюсона (PDF). Том 35: Восьмеричный путь: красота четвертой кривой Кляйна. Публикации ИИГС. С. 1–7.
- ^ "Обзор книги МАА Восьмеричный путь: красота кривой четвертой степени Кляйна". Maa.org. 14 ноября 1993 г.. Получено 13 августа 2009.
- ^ "Путеводитель по праздничным подаркам для математиков". Scientific American. 23 ноября 2014 г.. Получено 7 июн 2015.
- ^ Ханна, Ворон. "Галерея: Вирсавия Гроссман". Журнал Симметрия. Получено 7 июн 2015.
- ^ Флерон, Джулиан Ф .; Экке, Фолькер; фон Ренессе, Кристина; Хотчкисс, Филип К. (январь 2015 г.). Искусство и скульптура: математические исследования в области гуманитарных наук (2-е изд.). Проект «Открывая искусство математики».
- ^ Осинга, Хинке (2005). «Вязание крючком многообразия Лоренца». Оклендский университет. Архивировано из оригинал 10 апреля 2015 г.. Получено 12 октября 2015.
- ^ Осинга, Хинке М.; Краускопф, Бернд (2004). «Вязание крючком многообразия Лоренца». Математический интеллект. 26 (4): 25–37. CiteSeerX 10.1.1.108.4594. Дои:10.1007 / BF02985416. S2CID 119728638.
- ^ Дитц, Ада К. (1949). Алгебраические выражения в тканях ручной работы (PDF). Луисвилл, Кентукки: Маленький ткацкий станок. Архивировано из оригинал (PDF) на 2016-02-22. Получено 2015-06-26.
- ^ Хендерсон, Дэвид; Таймина, Дайна (2001). «Вязание крючком гиперболической плоскости» (PDF). Математический интеллигент. 23 (2): 17–28. Дои:10.1007 / BF03026623. S2CID 120271314..
- ^ Барнетт, Ребекка (31 января 2017 г.). «Галерея: Что происходит, когда вы смешиваете математику, коралл и вязание крючком? Это потрясающе». Ideas.TED.com. Получено 28 октября 2019.
- ^ Миллер, Дж. С. П. (1970). «Периодические леса низкорослых деревьев». Философские труды Лондонского королевского общества. Серия А, Математические и физические науки. 266 (1172): 63–111. Bibcode:1970РСПТА.266 ... 63М. Дои:10.1098 / рста.1970.0003. JSTOR 73779. S2CID 123330469.
- ^ "Пэт Эшфорт и Стив Пламмер - математики". Шерстяные мысли. Получено 4 октября 2015.
- ^ Уорд, Марк (20 августа 2012 г.). «Новое изобретение вязания: математика, феминизм и металл». Новости BBC. BBC. Получено 23 сентября 2015.
- ^ Эшфорт, Пэт; Пламмер, Стив. «Губка Менгера». Грязные мысли: в погоне за искусной математикой. Получено 23 сентября 2015.
- ^ Эшфорт, Пэт; Пламмер, Стив. «Афганцы для школ». Шерстяные мысли: Матганы. Получено 23 сентября 2015.
- ^ «Матганы с разницей». Журнал "Просто вязание". 1 июля 2008 г. Архивировано с оригинал 25 сентября 2015 г.. Получено 23 сентября 2015. Цитировать журнал требует
| журнал =(помощь) - ^ Жуффре, Esprit (1903). Образец геометрии в четырех измерениях и введение в геометрию в измерениях (На французском). Париж: Готье-Виллар. OCLC 1445172. Получено 26 сентября 2015.
- ^ Секель, Элен (1994). "Антология ранних комментариев к Les Demoiselles d'Avignon"Уильям Рубин; Элен Секель; Джудит Казинс (ред.). Les Demoiselles d'Avignon. Нью-Йорк: Музей современного искусства. п. 264. ISBN 978-0-87070-162-7.
- ^ "Джотто ди Бондоне и ассистенты: триптих Стефанески". Ватикан. Получено 16 сентября 2015.
- ^ Гэмвелл, Линн (2015). Математика и искусство: история культуры. Издательство Принстонского университета. С. 337–338. ISBN 978-0-691-16528-8.
- ^ Купер, Джонатан (5 сентября 2007 г.). «Искусство и математика». Получено 5 сентября 2015.
- ^ Хофштадтер, Дуглас Р. (1980). Гедель, Эшер, Бах: вечная золотая коса. Пингвин. п. 627. ISBN 978-0-14-028920-6.
- ^ Холл, Джеймс (10 июня 2011 г.). Выставка «Рене Магритт: принцип удовольствия». Хранитель. Получено 5 сентября 2015.
- ^ а б Хофштадтер, Дуглас Р. (1980). Гедель, Эшер, Бах: вечная золотая коса. Пингвин. С. 98–99, 690–717. ISBN 978-0-394-74502-2.
- ^ Кинг, Эллиотт (2004). Адес, Рассвет (ред.). Дали. Милан: Bompiani Arte. С. 418–421.
- ^ «Каменная балансировка» (PDF). Ежемесячная математика (29). Июль 2013. Получено 10 июн 2017.
- ^ де Смит, Б. (2003). "Математическая структура галереи печати Эшера". Уведомления Американского математического общества. 50 (4): 446–451.
- ^ Ленстра, Хендрик; Де Смит, Барт. «Применение математики в галерее печати Эшера». Лейденский университет. Получено 10 ноября 2015.
- ^ Станек, Бекка (16 июня 2014 г.). «Ван Гог и алгоритм: как математика может спасти искусство». Журнал Тайм. Получено 4 сентября 2015.
- ^ Сипикс, Мишель (18 мая 2009 г.). «Проект Ван Гога: искусство встречается с математикой в рамках текущего международного исследования». Общество промышленной и прикладной математики. Архивировано из оригинал 7 сентября 2015 г.. Получено 4 сентября 2015.
- ^ Эммерлинг, Леонхард (2003). Джексон Поллок, 1912–1956 гг.. п. 63. ISBN 978-3-8228-2132-9.
- ^ Тейлор, Ричард П .; Micolich, Adam P .; Джонас, Дэвид (июнь 1999 г.). «Фрактальный анализ капельных картин Поллока» (PDF). Природа. 399 (6735): 422. Bibcode:1999Натура.399..422Т. Дои:10.1038/20833. S2CID 204993516. Архивировано из оригинал (PDF) на 2015-08-16.
- ^ Тейлор, Ричард; Micolich, Adam P .; Джонас, Дэвид (октябрь 1999 г.). «Фрактальный экспрессионизм: можно ли использовать науку для дальнейшего понимания искусства?». Мир физики. 12 (10): 25–28. Дои:10.1088/2058-7058/12/10/21. Архивировано из оригинал на 2012-08-05.
Поллок умер в 1956 году, до того, как были обнаружены хаос и фракталы. Поэтому маловероятно, что Поллок сознательно понимал фракталы, которые он рисовал. Тем не менее, его введение фракталов было преднамеренным. Например, цвет якорного слоя был выбран так, чтобы обеспечить наиболее резкий контраст с фоном холста, и этот слой также занимает больше пространства холста, чем другие слои, предполагая, что Поллок хотел, чтобы этот сильно фрактальный якорный слой визуально доминировал над картиной. Кроме того, после того, как картины были закончены, он стыковал холст, чтобы удалить области около края холста, где плотность рисунка была менее однородной.
- ^ Кинг, М. (2002). «От Макса Эрнста до Эрнста Маха: эпистемология в искусстве и науке» (PDF). Получено 17 сентября 2015.
- ^ Доджсон, Н. А. (2012). «Математическая характеристика полосатых картин Бриджит Райли» (PDF). Журнал математики и искусств. 5 (2–3): 89–106. Дои:10.1080/17513472.2012.679468. S2CID 10349985.
в течение начала 1980-х паттерны Райли менялись от более регулярных к более случайным (характеризуемым глобальной энтропией) без потери своей ритмической структуры (характеризуемой локальной энтропией). Это отражает описание Куделкой ее художественного развития.
- ^ Кукер, Феликс (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. С. 116–120. ISBN 978-0-521-72876-8.
- ^ Трейбергс, Андрейс (24 июля 2001 г.). «Геометрия перспективного рисования на компьютере». Университет Юты. Получено 5 сентября 2015.
- ^ Гэмвелл, Линн (2015). Математика и искусство: история культуры. Издательство Принстонского университета. п. xviii. ISBN 978-0-691-16528-8.
- ^ Малькевич, Иосиф. «Математика и искусство. 6. Оригами». Американское математическое общество. Получено 1 сентября 2015.
- ^ Т. Сундара Рао (1893). Геометрические упражнения в складывании бумаги. Аддисон.
- ^ Джастин, Дж. (Июнь 1986 г.). «Математика оригами, часть 9». Британское Оригами: 28–30..
- ^ Альсина, Клауди; Нельсен, Роджер (2010). Очаровательные доказательства: путешествие в элегантную математику. Математические экспозиции Дольчиани. 42. Математическая ассоциация Америки. п. 57. ISBN 978-0-88385-348-1.
- ^ Альперин, Роджер С .; Ланг, Роберт Дж. (2009). "Аксиомы одно-, двух- и многовариантного оригами" (PDF). 4OSME.
- ^ Мир геометрических игрушек, Оригами Весна, Август 2007 г.
- ^ Кукер, Феликс (2013). Многообразные зеркала: пути пересечения искусства и математики. Издательство Кембриджского университета. С. 163–166. ISBN 978-0-521-72876-8.
- ^ Гэмвелл, Линн (2015). Математика и искусство: история культуры. Издательство Принстонского университета. С. 406–410. ISBN 978-0-691-16528-8.
- ^ Гика, Матила (2003). Геометрия искусства и жизни. Дувр. стр. ix – xi. ISBN 978-0-486-23542-4.
- ^ Лоулор, Роберт (1982). Сакральная геометрия: философия и практика. Темза и Гудзон. ISBN 978-0-500-81030-9.
- ^ а б Калтер, Пол (1998). «Небесные темы в искусстве и архитектуре». Дартмутский колледж. Получено 5 сентября 2015.
- ^ Мэддокс, Фиона (21 ноября 2014 г.). «10 лучших работ Уильяма Блейка». Хранитель. Получено 25 декабря 2019.
- ^ "Уильям Блейк, Ньютон, 1795–1805 гг.". Тейт. Октябрь 2018. Архивировано с оригинал 28 марта 2019 г.
- ^ Ливио, Марио (Ноябрь 2002 г.). «Золотое сечение и эстетика». Получено 26 июн 2015.
внешняя ссылка
- Организация мостов конференция о связи искусства и математики
- Преодоление разрыва между математикой и искусством - Слайд-шоу от Scientific American
- Открытие искусства математики
- Математика и искусство – AMS
- Математика и искусство – Разрезать узел
- Математические образы – Американское математическое общество
- Математика в искусстве и архитектуре - Национальный университет Сингапура
- Математическое искусство - Виртуальный математический музей
- Когда искусство и математика сталкиваются – Новости науки
- Почему история математики - это также история искусства: Линн Гэмвелл в Хранитель