Энтропия - Entropy
| Энтропия | |
|---|---|
Общие символы | S |
| Единица СИ | джоули на кельвин (J⋅K−1) |
| В Базовые единицы СИ | кг⋅м2⋅s−2⋅K−1 |
| Термодинамика | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 Классический Тепловой двигатель Карно | ||||||||||||
| ||||||||||||
| ||||||||||||
| Энтропийные статьи |
|---|
В статистическая механика, энтропия является обширная собственность из термодинамическая система. Он определяет количество Ω микроскопических конфигураций (известных как микросостояния ), которые согласуются с макроскопическими величинами, характеризующими систему (такими как ее объем, давление и температура).[1] В предположении, что каждое микросостояние равновероятно, энтропия это натуральный логарифм числа микросостояний, умноженное на Постоянная Больцмана kB. Формально (в предположении равновероятных микросостояний)
Макроскопические системы обычно имеют очень большое количество Ω возможных микроскопических конфигураций. Например, энтропия идеальный газ пропорциональна количеству молекул газа N. Количество молекул в 22,4 л газа при стандартная температура и давление примерно 6,022 × 1023 (в Число Авогадро ).
В второй закон термодинамики утверждает, что энтропия изолированной системы никогда не уменьшается со временем. Изолированные системы спонтанно развиваются в сторону термодинамическое равновесие, состояние с максимальной энтропией. Неизолированные системы, например организмы, могут потерять энтропию при условии, что энтропия их среды увеличивается по крайней мере на эту величину, так что полная энтропия либо увеличивается, либо остается постоянной. Следовательно, энтропия в конкретной системе может уменьшаться до тех пор, пока полная энтропия Вселенная не. Энтропия - это функция состояние системы, поэтому изменение энтропии системы определяется ее начальным и конечным состояниями. В идеализации процесса обратимый, энтропия не меняется, а необратимые процессы всегда увеличивают полную энтропию.
Поскольку энтропия определяется количеством случайных микросостояний, она связана с количеством дополнительной информации, необходимой для определения точного физического состояния системы с учетом ее макроскопических характеристик. По этой причине часто говорят, что энтропия - это выражение беспорядка или случайность системы или отсутствия информации о ней.[2] Концепция энтропии играет центральную роль в теория информации.
История

Французский математик Лазар Карно предложил в своей статье 1803 г. Основные принципы равновесия и движения что в любой машине ускорения и удары движущихся частей представляют собой потери момент активности; в любом естественном процессе существует внутренняя тенденция к рассеиванию полезных энергия. Основываясь на этой работе, в 1824 году сын Лазара Сади Карно опубликовано Размышления о движущей силе огня, который утверждал, что во всех тепловых двигателях, когда бы "калорийность "(то, что сейчас известно как высокая температура ) падает из-за перепада температур, работает или сила мотивации может возникнуть в результате его падения с горячего тела на холодное. Он провел аналогию с тем, как вода падает в водяное колесо. Это было раннее понимание второй закон термодинамики.[3] Карно основывал свои взгляды на тепло частично на «ньютоновской гипотезе» начала 18 века, согласно которой и тепло, и свет были типами неразрушимых форм материи, которые притягиваются и отталкиваются другой материей, а частично - на современных взглядах на Граф Рамфорд который показал (1789 г.), что тепло может создаваться трением, как при обработке стволов пушек.[4] Карно рассуждал, что если тело рабочего тела, такое как тело пара, возвращается в исходное состояние в конце полного цикл двигателя, что «в состоянии рабочего тела не происходит никаких изменений».
В первый закон термодинамики, выведенные из экспериментов по тепловому трению Джеймс Джоуль в 1843 г. выражает понятие энергии и ее сохранение во всех процессах; первый закон, однако, не может количественно оценить влияние трение и рассеяние.
В 1850-1960-х годах немецкий физик Рудольф Клаузиус возразил против предположения, что в рабочем теле не происходит никаких изменений, и дал этому "изменению" математическую интерпретацию, поставив под сомнение природу внутренних потерь полезного тепла при выполнении работы, например тепло, выделяемое трением.[5] Клаузиус описал энтропию как содержание трансформации, т. е. диссипативное использование энергии термодинамическая система или же рабочий орган из химические вещества во время смены государственный.[5] Это контрастировало с более ранними взглядами, основанными на теориях Исаак Ньютон, это тепло было неразрушимой частицей, имеющей массу.
Позже такие ученые, как Людвиг Больцманн, Джозайя Уиллард Гиббс, и Джеймс Клерк Максвелл дал энтропии статистическую основу. В 1877 году Больцман представил вероятностный способ измерения энтропии ансамбля идеальный газ частиц, в которых он определил энтропию как пропорциональную натуральному логарифму числа микросостояний, в которых может находиться такой газ. Отныне основная проблема в статистическая термодинамика заключалась в том, чтобы определить распределение заданного количества энергии E над N идентичные системы.Каратеодори связана энтропия с математическим определением необратимости в терминах траекторий и интегрируемости.
Этимология
В 1865 году Клаузиус назвал концепцию S, «разница величины, которая зависит от конфигурации системы», энтропия (Энтропия) после греческого слова «преобразование».[6] Он дает «трансформационное содержание» (Verwandlungsinhalt) как синоним, параллельно с его «термическим и эргональным содержанием» (Wärme- und Werkinhalt) как имя U, но предпочитая термин энтропия как близкая параллель слову энергия, поскольку он нашел эти концепции почти «аналогичными по своему физическому значению».[6] Этот термин образовался заменой корня из ἔργον ('работа') τροπή («преобразование»).[7]
Определения и описания
Уиллард Гиббс, Графические методы в термодинамике жидкостей[8]
Есть два эквивалентных определения энтропии: термодинамическое определение и определение статистической механики. Исторически первым было разработано классическое определение термодинамики. в классическая термодинамика точки зрения микроскопические детали системы не рассматриваются. Вместо этого поведение системы описывается с помощью набора эмпирически определенных термодинамических переменных, таких как температура, давление, энтропия и теплоемкость. Описание классической термодинамики предполагает состояние равновесия, хотя в последнее время были предприняты попытки разработать полезные определения энтропии в неравновесный системы тоже.
В статистическое определение энтропии и другие термодинамические свойства были развиты позже. С этой точки зрения термодинамические свойства определяются в терминах статистики движений микроскопических составляющих системы, моделируемых сначала классически, например Ньютоновские частицы, составляющие газ, а позже квантово-механически (фотоны, фононы, спины и т. д.).
Функция государства
Есть много термодинамические свойства которые функции государства. Это означает, что в определенном термодинамическом состоянии (которое не следует путать с микроскопическим состоянием системы) эти свойства имеют определенное значение. Часто, если определены два свойства системы, то определяется состояние и значения других свойств также могут быть определены. Например, количество газа при определенной температуре и давлении имеет свое состояние, фиксированное этими значениями, и, таким образом, имеет определенный объем, который определяется этими значениями. Другой пример: система, состоящая из чистого вещества одного фаза при определенной однородной температуре и давлении определяется (и, таким образом, является конкретным состоянием) и находится не только в определенном объеме, но также в определенной энтропии.[9] Тот факт, что энтропия является функцией состояния, является одной из причин ее полезности. В цикле Карно рабочая жидкость возвращается в то же состояние, в котором она была в начале цикла, следовательно, линейный интеграл любой функции состояния, такой как энтропия, в этом обратимом цикле равна нулю.
Обратимый процесс
Энтропия сохраняется для обратимый процесс. Обратимый процесс - это процесс, который не отклоняется от термодинамического равновесия, производя при этом максимальную работу. Любой процесс, который происходит достаточно быстро, чтобы отклониться от теплового равновесия, не может быть обратимым. В этих случаях энергия теряется на тепло, общая энтропия увеличивается, а также теряется возможность выполнения максимальной работы при переходе. Более конкретно, полная энтропия сохраняется в обратимом процессе и не сохраняется в необратимом процессе.[10] Например, в цикле Карно, в то время как тепловой поток от горячего резервуара к холодному резервуару представляет собой увеличение энтропии, рабочий выход, если он обратимо и идеально сохранен в каком-либо механизме накопления энергии, представляет собой уменьшение энтропии, которое можно было бы использовать. для работы теплового двигателя в обратном направлении и возврата в предыдущее состояние, таким образом, общий изменение энтропии все время равно нулю, если весь процесс обратим. Необратимый процесс увеличивает энтропию.[11]
Цикл Карно
Понятие энтропии возникло из Рудольф Клаузиус исследование Цикл Карно.[12] В цикле Карно тепло QЧАС абсорбируется изотермически при температуре ТЧАС из «горячего» резервуара и изотермически выделяется в виде тепла QC в «холодный» резервуар на ТC. Согласно принципу Карно, работай может производиться системой только при разнице температур, и работа должна зависеть от разницы температуры и поглощенного тепла (QЧАС). Карно не различал QЧАС и QC, поскольку он использовал неверную гипотезу, что теория калорий было действительным, и, следовательно, тепло сохранялось (неверное предположение, что QЧАС и QC были равны), когда на самом деле QЧАС больше, чем QC.[13][14] Усилиями Клаузиуса и Кельвин, теперь известно, что максимальная работа, которую может произвести тепловой двигатель, является произведением КПД Карно и тепла, поглощаемого из горячего резервуара:
(1)
Чтобы вывести эффективность Карно, которая 1 − ТC/ТЧАС (число меньше единицы), Кельвину пришлось оценить отношение производимой работы к теплу, поглощенному во время изотермического расширения, с помощью уравнения Карно-Клапейрона, которое содержало неизвестную функцию, называемую функцией Карно. Возможность того, что функция Карно могла быть температурой, измеренной от нулевой температуры, была предложена Джоуль в письме Кельвину. Это позволило Кельвину установить свою абсолютную шкалу температуры.[15] Также известно, что работа, производимая системой, представляет собой разницу между теплотой, поглощенной из горячего резервуара, и теплом, отдаваемым холодному резервуару:
(2)
Поскольку последнее верно для всего цикла, это дало Клаузиусу понять, что на каждой стадии цикла работа и тепло не будут равны, а скорее их различие будет функцией состояния, которая исчезнет по завершении цикла. Функция состояния была названа внутренней энергией и стала первый закон термодинамики.[16]
Теперь приравнивая (1) и (2) дает
или же
Это означает, что существует функция состояния, которая сохраняется в течение полного цикла цикла Карно. Клаузиус назвал эту функцию состояния энтропия. Можно видеть, что энтропия была открыта с помощью математики, а не лабораторных результатов. Это математическая конструкция, не имеющая простой физической аналогии. Это делает концепцию несколько неясной или абстрактной, сродни тому, как возникла концепция энергии.
Затем Клаузиус спросил, что произойдет, если система произведет меньше работы, чем предсказывает принцип Карно. Правая часть первого уравнения будет верхней границей объема работы системы, которая теперь будет преобразована в неравенство
Когда второе уравнение используется для выражения работы как разницы в теплотах, мы получаем
- или же
Таким образом, холодному резервуару передается больше тепла, чем в цикле Карно. Если обозначить энтропии через Sя = Qя/Тя для двух состояний, то указанное выше неравенство можно записать как уменьшение энтропии
- или же
Энтропия, которая покидает систему, больше энтропии, которая входит в систему, подразумевая, что какой-то необратимый процесс не позволяет циклу производить максимальное количество работы, предсказываемое уравнением Карно.
Цикл Карно и КПД полезны, потому что они определяют верхнюю границу возможного объема работы и КПД любой классической термодинамической системы. Другие циклы, такие как Цикл Отто, Дизельный цикл и Цикл Брайтона, могут быть проанализированы с точки зрения цикла Карно. Любая машина или процесс, который преобразует тепло в работу и, как утверждается, обеспечивает эффективность, превышающую эффективность Карно, нежизнеспособна, поскольку нарушает второй закон термодинамики. Для очень небольшого числа частиц в системе необходимо использовать статистическую термодинамику. Эффективность таких устройств, как фотоэлектрические элементы, требует анализа с точки зрения квантовой механики.
Классическая термодинамика
| Сопряженные переменные термодинамики | |
|---|---|
| Давление | Объем |
| (Стресс ) | (Напряжение ) |
| Температура | Энтропия |
| Химический потенциал | Номер частицы |
Термодинамическое определение энтропии было разработано в начале 1850-х гг. Рудольф Клаузиус и по существу описывает, как измерить энтропию изолированная система в термодинамическое равновесие со своими частями. Клаузиус создал термин энтропия как обширную термодинамическую переменную, полезную для характеристики Цикл Карно. Было обнаружено, что теплопередача по этапам изотермы цикла Карно пропорциональна температуре системы (известной как ее абсолютная температура ). Это соотношение было выражено в приращениях энтропии, равных отношению приращения теплопередачи к температуре, которая, как было обнаружено, изменяется в термодинамическом цикле, но в конечном итоге возвращается к тому же значению в конце каждого цикла. Таким образом, было обнаружено, что это функция государства, а именно термодинамическое состояние системы.
Хотя Клаузиус основывал свое определение на обратимом процессе, существуют также необратимые процессы, которые изменяют энтропию. После второй закон термодинамики, энтропия изолированного система всегда увеличивается для необратимых процессов. Разница между изолированной системой и закрытой системой заключается в том, что тепло может нет поток в изолированную систему и из нее, но возможен поток тепла в закрытую систему и из нее. Тем не менее, как для закрытых, так и для изолированных систем, а также в открытых системах могут иметь место необратимые термодинамические процессы.
Согласно Равенство Клаузиуса, для обратимого циклического процесса:Это означает линейный интеграл является независимый от пути.
Итак, мы можем определить функцию состояния S называется энтропией, которая удовлетворяет
Чтобы найти разницу энтропии между любыми двумя состояниями системы, интеграл должен быть вычислен для некоторого обратимого пути между начальным и конечным состояниями.[17] Поскольку энтропия является функцией состояния, изменение энтропии системы для необратимого пути такое же, как и для обратимого пути между теми же двумя состояниями.[18] Однако изменение энтропии в окружающей среде иное.
Мы можем получить изменение энтропии, только интегрировав приведенную выше формулу. Чтобы получить абсолютное значение энтропии, нам понадобится третий закон термодинамики, в котором говорится, что S = 0 при абсолютный ноль для идеальных кристаллов.
С макроскопической точки зрения в классическая термодинамика энтропия интерпретируется как государственная функция из термодинамическая система: то есть свойство, зависящее только от текущего состояния системы, независимо от того, как это состояние было достигнуто. В любом процессе, когда система теряет энергию ΔE, а его энтропия падает на ΔS, количество не менее Тр ΔS из этой энергии должна быть отдана окружению системы в качестве непригодного тепла (Тр - температура внешней среды системы). В противном случае процесс не может продолжаться. В классической термодинамике энтропия системы определяется, только если она находится в термодинамическое равновесие.
Статистическая механика
Статистическое определение было разработано Людвиг Больцманн в 1870-х годах путем анализа статистического поведения микроскопических компонентов системы. Больцман показал, что это определение энтропии эквивалентно термодинамической энтропии с точностью до постоянного множителя, известного как Постоянная Больцмана. Таким образом, термодинамическое определение энтропии обеспечивает экспериментальное определение энтропии, в то время как статистическое определение энтропии расширяет концепцию, обеспечивая объяснение и более глубокое понимание ее природы.
В интерпретация энтропии в статистической механике мера неопределенности, или путаница во фразе Гиббс, который остается в системе после того, как были учтены ее наблюдаемые макроскопические свойства, такие как температура, давление и объем. Для данного набора макроскопических переменных энтропия измеряет степень, в которой вероятность системы распределена по различным возможным микросостояния. В отличие от макросостояния, которое характеризует четко наблюдаемые средние величины, микросостояние определяет все молекулярные детали системы, включая положение и скорость каждой молекулы. Чем больше таких состояний доступно системе с заметной вероятностью, тем больше энтропия. В статистической механике энтропия - это мера количества способов организации системы, часто принимаемая за меру «беспорядка» (чем выше энтропия, тем выше беспорядок).[19][20][21] Это определение описывает энтропию как пропорциональную натуральному логарифму числа возможных микроскопических конфигураций отдельных атомов и молекул системы (микросостояния ), которое могло вызвать наблюдаемое макроскопическое состояние (макросостояние ) системы. Константа пропорциональности - это Постоянная Больцмана.
Постоянная Больцмана и, следовательно, энтропия, имеют размеры из энергия деленное на температура, который имеет единицу джоули на кельвин (J⋅K−1) в Международная система единиц (или кг⋅м2⋅s−2⋅K−1 в базовых единицах). Энтропия вещества обычно дается как интенсивное свойство - либо энтропия на единицу масса (Единица СИ: J⋅K−1⋅кг−1) или энтропия на единицу количество вещества (Единица СИ: J⋅K−1⋅mol−1).
В частности, энтропия - это логарифмический мера количества состояний со значительной вероятностью быть занятыми:
или, что то же самое, ожидаемое значение логарифм вероятности что микрогосударство занято
куда kB это Постоянная Больцмана, равно 1.38065×10−23 Дж / КСуммирование ведется по всем возможным микросостояниям системы, и пя вероятность того, что система находится в я-го микросостояние.[22] Это определение предполагает, что базовый набор состояний выбран так, что нет информации об их относительных фазах. В другом базисе более общее выражение
куда это матрица плотности, является след и это матричный логарифм. Такая формулировка матрицы плотности не требуется в случаях теплового равновесия, пока базисные состояния выбраны как собственные состояния энергии. Для большинства практических целей это можно рассматривать как фундаментальное определение энтропии, поскольку все остальные формулы для S может быть выведено из него математически, но не наоборот.
В том, что было названо фундаментальное предположение статистической термодинамики или же фундаментальный постулат статистической механики, предполагается, что занятие любого микросостояния равновероятно (т. е. пя = 1 / Ω, где Ω - количество микросостояний); это предположение обычно оправдывается для изолированной системы, находящейся в равновесии.[23] Тогда предыдущее уравнение сводится к
В термодинамике такой системой считается система, в которой объем, количество молекул и внутренняя энергия фиксированы ( микроканонический ансамбль ).
Для данной термодинамической системы избыточная энтропия определяется как энтропия за вычетом энтропии идеального газа при той же плотности и температуре, величина, которая всегда отрицательна, потому что идеальный газ максимально разупорядочен.[24] Эта концепция играет важную роль в теории жидкого состояния. Например, принцип масштабирования избыточной энтропии Розенфельда[25][26] утверждает, что приведенные транспортные коэффициенты на двумерной фазовой диаграмме являются функциями, однозначно определяемыми избыточной энтропией.[27][28]
Наиболее общая интерпретация энтропии - это мера нашей неопределенности в отношении системы. В состояние равновесия системы максимизирует энтропию, потому что мы потеряли всю информацию о начальных условиях, кроме сохраняемых переменных; максимизация энтропии максимизирует наше незнание деталей системы.[29] Эта неопределенность не повседневного субъективного характера, а скорее неопределенность, присущая экспериментальному методу и интерпретационной модели.
Интерпретативная модель играет центральную роль в определении энтропии. Приведенный выше квалификатор «для данного набора макроскопических переменных» имеет глубокие последствия: если два наблюдателя используют разные наборы макроскопических переменных, они видят разные энтропии. Например, если наблюдатель A использует переменные U, V и W, а наблюдатель B использует U, V, W, Икс, затем, изменив Икс, наблюдатель B может вызвать эффект, который для наблюдателя A выглядит как нарушение второго закона термодинамики. Другими словами: выбираемый набор макроскопических переменных должен включать все, что может измениться в эксперименте, иначе можно увидеть уменьшение энтропии![30]
Энтропию можно определить для любого Марковские процессы с обратимая динамика и подробный баланс свойство.
У Больцмана 1896 г. Лекции по теории газа, он показал, что это выражение дает меру энтропии для систем атомов и молекул в газовой фазе, тем самым обеспечивая меру энтропии классической термодинамики.
Энтропия системы

Энтропия возникает непосредственно из Цикл Карно. Его также можно описать как обратимое тепло, деленное на температуру. Энтропия - фундаментальная функция состояния.
В термодинамическая система давление, плотность и температура со временем становятся однородными, поскольку состояние равновесия имеет более высокий вероятность (более возможно комбинации из микросостояния ), чем в любом другом штате.
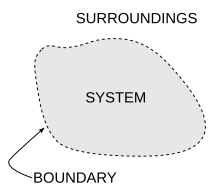
Например, для стакана лед вода в воздухе на комнатная температура, разница в температуре между теплой комнатой (окружающей средой) и холодным стаканом льда и воды (система, а не часть комнаты) начинает выравниваться по мере того, как части тепловая энергия из теплого окружения распространяется в более прохладную систему льда и воды. Со временем температура стакана и его содержимого сравняется с температурой в помещении. Другими словами, энтропия комнаты уменьшилась, поскольку часть ее энергии была передана льду и воде.
Однако, как вычислено в примере, энтропия системы льда и воды увеличилась больше, чем энтропия окружающей комнаты уменьшилась. В изолированная система Например, вместе взятые, например, вода в помещении и ледяная вода, распределение энергии от более теплой к более холодной всегда приводит к чистому увеличению энтропии. Таким образом, когда «вселенная» комнаты и системы ледяной воды достигла температурного равновесия, изменение энтропии по сравнению с начальным состоянием является максимальным. Энтропия термодинамическая система является мерой того, насколько далеко продвинулось выравнивание.
Термодинамическая энтропия - это несохраняемая государственная функция это имеет большое значение в науках о физика и химия.[19][31] Исторически концепция энтропии развивалась, чтобы объяснить, почему некоторые процессы (разрешенные законами сохранения) происходят спонтанно, в то время как их развороты времени (также разрешено законами о сохранении) нет; системы имеют тенденцию прогрессировать в направлении увеличения энтропии.[32][33] За изолированные системы, энтропия никогда не уменьшается.[31] Этот факт имеет несколько важных последствий для наука: во-первых, это запрещает "вечное движение "машины; во-вторых, это подразумевает стрела энтропии имеет то же направление, что и стрела времени. Увеличение энтропии соответствует необратимым изменениям в системе, потому что некоторая энергия расходуется в виде отработанного тепла, ограничивая объем работы, которую может выполнять система.[19][20][34][35]
В отличие от многих других функций состояния, энтропию нельзя непосредственно наблюдать, но ее необходимо вычислить. Энтропию вещества можно рассчитать как стандартная молярная энтропия из абсолютный ноль (также известное как абсолютная энтропия) или как разность энтропии от некоторого другого исходного состояния, определяемого как нулевая энтропия. Энтропия имеет измерение из энергия деленное на температура, который имеет единицу джоули на кельвин (Дж / К) в Международная система единиц. Хотя это те же единицы, что и теплоемкость, эти два понятия различны.[36] Энтропия не является постоянной величиной: например, в изолированной системе с неоднородной температурой тепло может необратимо течь, и температура станет более однородной, так что энтропия возрастет. В второй закон термодинамики утверждает, что энтропия закрытой системы может увеличиваться или оставаться постоянной. Химические реакции вызывают изменения энтропии, и энтропия играет важную роль в определении того, в каком направлении спонтанно протекает химическая реакция.
Одно словарное определение энтропии состоит в том, что это «мера тепловой энергии на единицу температуры, которая недоступна для полезной работы». Например, вещество при постоянной температуре имеет максимальную энтропию и не может управлять тепловым двигателем. Вещество с неоднородной температурой имеет более низкую энтропию (чем если бы распределение тепла было равномерным), и часть тепловой энергии может приводить в движение тепловую машину.
Частный случай увеличения энтропии, энтропия смешения, возникает при смешивании двух или более разных веществ. Если вещества имеют одинаковую температуру и давление, нет чистого обмена теплом или работы - изменение энтропии полностью происходит за счет смешивания разных веществ. На статистически-механическом уровне это происходит из-за изменения доступного объема на частицу при перемешивании.[37]
Эквивалентность определений
Доказательства эквивалентности определения энтропии в статистической механике ( Формула энтропии Гиббса ) и в классической термодинамике ( вместе с фундаментальное термодинамическое соотношение ) известны микроканонический ансамбль, то канонический ансамбль, то большой канонический ансамбль, а изотермически-изобарный ансамбль. Эти доказательства основаны на плотности вероятности микросостояний обобщенного Распределение Больцмана и идентификация термодинамической внутренней энергии как среднего по ансамблю .[38] Затем термодинамические соотношения используются для вывода хорошо известного Формула энтропии Гиббса. Однако эквивалентность между Формула энтропии Гиббса и термодинамическое определение энтропии не является фундаментальным термодинамическим соотношением, а скорее является следствием формы обобщенного Распределение Больцмана.[39]
Второй закон термодинамики
Второй закон термодинамики требует, чтобы общая энтропия любой системы не могла уменьшаться иначе как за счет увеличения энтропии какой-либо другой системы. Следовательно, в системе, изолированной от окружающей среды, энтропия этой системы не имеет тенденции к уменьшению. Отсюда следует, что тепло не может течь от более холодного тела к более горячему без приложения работы (наведения порядка) к более холодному телу. Во-вторых, никакое устройство, работающее в цикле, не может производить чистую работу из единственного температурного резервуара; для производства сети требуется поток тепла от более горячего резервуара к более холодному резервуару или один расширяющийся резервуар, подвергающийся адиабатическое охлаждение, который выполняет адиабатическая работа. В результате отсутствует возможность вечное движение система. Отсюда следует, что уменьшение увеличения энтропии в заданном процессе, таком как химическая реакция, означает, что он энергетически более эффективен.
Из второго начала термодинамики следует, что энтропия неизолированной системы может уменьшаться. An кондиционер, например, может охлаждать воздух в комнате, тем самым уменьшая энтропию воздуха этой системы. Тепло, выбрасываемое из комнаты (системы), которое кондиционер переносит и отводит в наружный воздух, всегда вносит больший вклад в энтропию окружающей среды, чем уменьшение энтропии воздуха этой системы. Таким образом, общая энтропия комнаты плюс энтропия окружающей среды увеличивается в соответствии со вторым законом термодинамики.
В механике второй закон в сочетании с фундаментальное термодинамическое соотношение накладывает ограничения на способность системы выполнять полезная работа.[40] Изменение энтропии системы при температуре Т поглощение бесконечно малого количества тепла δqобратимым образом, дается δq/Т. Точнее, энергия Тр S недоступен для полезной работы, где Тр - это температура самого холодного доступного резервуара или радиатора вне системы. Для дальнейшего обсуждения см. Эксергия.
Статистическая механика демонстрирует, что энтропия определяется вероятностью, что позволяет уменьшить беспорядок даже в изолированной системе. Хотя это возможно, такое событие имеет небольшую вероятность возникновения, что делает его маловероятным.[41]
Применимость второго закона термодинамики ограничена системами вблизи или в состояние равновесия.[42] В то же время законы, управляющие системами, далекими от равновесия, все еще остаются предметом споров. Одним из руководящих принципов для таких систем является принцип максимального производства энтропии.[43][44] Он утверждает, что неравновесные системы развиваются таким образом, чтобы максимизировать производство энтропии.[45][46]
Приложения
Основное термодинамическое соотношение
Энтропия системы зависит от ее внутренней энергии и внешних параметров, таких как объем. В термодинамическом пределе это приводит к уравнению, связывающему изменение внутренней энергии U к изменению энтропии и внешних параметров. Это отношение известно как фундаментальное термодинамическое соотношение. Если внешнее давление п имеет значение V как единственный внешний параметр, это соотношение:
Поскольку внутренняя энергия и энтропия являются монотонными функциями температуры Т, подразумевая, что внутренняя энергия фиксирована при задании энтропии и объема, это соотношение справедливо, даже если переход от одного состояния теплового равновесия к другому с бесконечно большей энтропией и объемом происходит неквазистатическим образом (так что во время этого изменение системы может быть очень далеко от теплового равновесия, и тогда энтропия, давление и температура всей системы могут не существовать).
Фундаментальное термодинамическое соотношение подразумевает множество термодинамических тождеств, которые действительны в целом, независимо от микроскопических деталей системы. Важными примерами являются Максвелл отношения и отношения между тепловыми мощностями.
Энтропия в химической термодинамике
Термодинамическая энтропия занимает центральное место в химическая термодинамика, что позволяет количественно оценить изменения и спрогнозировать результаты реакции. В второй закон термодинамики утверждает, что энтропия в изолированная система - сочетание изучаемой подсистемы и ее окружения - увеличивается при всех спонтанных химических и физических процессах. Уравнение Клаузиуса для δqrev/Т = ΔS вводит измерение изменения энтропии ΔS. Изменение энтропии описывает направление и количественно определяет величину простых изменений, таких как передача тепла между системами - всегда спонтанно от более горячего к более холодному.
Таким образом, термодинамическая энтропия имеет размерность энергии, деленную на температуру, и единица измерения джоуль на кельвин (Дж / К) в Международной системе единиц (СИ).
Термодинамическая энтропия - это обширный свойство, что означает, что оно масштабируется в соответствии с размером или экстентом системы. Во многих процессах полезно указывать энтропию как интенсивное свойство независимо от размера, как специфическая энтропийная характеристика изучаемой системы. Удельная энтропия может быть выражена относительно единицы массы, обычно килограмм (единица измерения: Дж⋅кг−1⋅K−1). Как вариант, в химии его еще называют одним крот вещества, и в этом случае он называется молярная энтропия с единицей J⋅mol−1⋅K−1.
Таким образом, когда один моль вещества около 0 К согревается своим окружением до 298 К, сумма приращений значений qrev/Т составляют стандартную молярную энтропию каждого элемента или соединения, показатель количества энергии, запасаемой веществом в 298 К.[47][48] Изменение энтропии также измеряет смешивание веществ как сумму их относительных количеств в конечной смеси.[49]
Энтропия не менее важна для предсказания степени и направления сложных химических реакций. Для таких приложений ΔS должны быть включены в выражение, которое включает как систему, так и ее окружение, ΔSвселенная = ΔSокружение + ΔS система. Это выражение через несколько шагов становится Свободная энергия Гиббса уравнение для реагентов и продуктов в системе: Δграмм [изменение свободной энергии Гиббса системы] = ΔЧАС [изменение энтальпии] - Т ΔS [изменение энтропии].[47]
Уравнение баланса энтропии для открытых систем

В химическая инженерия, принципы термодинамики обычно применяются к "открытые системы ", т.е. те, в которых тепло, работай, и масса поток через границу системы. Потоки обоих тепла () и работать, т.е. (шахтная работа ) и п(dV/dt) (работа давление-объем) через границы системы, как правило, вызывают изменения энтропии системы. Передача тепла влечет за собой перенос энтропии куда Т абсолютный термодинамическая температура системы в точке теплового потока. Если есть потоки массы через границы системы, они также влияют на общую энтропию системы. Этот учет в терминах тепла и работы действителен только для случаев, когда работа и теплопередача происходят по путям, физически отличным от путей входа и выхода вещества из системы.[50][51]
Чтобы вывести обобщенное уравнение баланса энтропии, мы начнем с общего уравнения баланса для изменения любого большое количество Θ в термодинамическая система, величина, которая может быть либо сохраняемой, например энергия, либо несохраняемой, например энтропией. Базовое универсальное выражение баланса утверждает, что dΘ / dt, то есть скорость изменения в системе, равна скорости, с которой Θ входит в систему на границах, минус скорость, с которой Θ покидает систему через границы системы, плюс скорость, с которой Θ генерируется в системе. Для открытой термодинамической системы, в которой тепло и работа передаются путями, отдельными от путей для переноса материи, с использованием этого общего уравнения баланса относительно скорости изменения во времени т энтропии огромного количества S, уравнение баланса энтропии:[52][примечание 1]
куда
- чистая скорость потока энтропии из-за потоков массы в систему и из системы (где энтропия на единицу массы).
- скорость потока энтропии из-за потока тепла через границу системы.
- скорость производство энтропии внутри системы. Это производство энтропии возникает в результате процессов внутри системы, включая химические реакции, диффузию внутреннего вещества, внутреннюю теплопередачу и фрикционные эффекты, такие как вязкость, возникающую в системе в результате передачи механической работы в систему или из нее.
Если имеется несколько тепловых потоков, член заменяется на куда тепловой поток и это температура на jпорт теплового потока в систему.
Формулы изменения энтропии для простых процессов
Для некоторых простых преобразований в системах постоянного состава изменения энтропии задаются простыми формулами.[53]
Изотермическое расширение или сжатие идеального газа
Для расширения (или сжатия) идеальный газ из первоначального объема и давление к окончательному тому и давление при любой постоянной температуре изменение энтропии определяется по формуле:
Здесь это количество родинки газа и это постоянная идеального газа. Эти уравнения также применимы для расширения в конечный вакуум или процесс дросселирования, где температура, внутренняя энергия и энтальпия для идеального газа остаются постоянными.
Охлаждение и обогрев
Для нагрева или охлаждения любой системы (газовой, жидкой или твердой) при постоянном давлении от начальной температуры до конечной температуры , изменение энтропии равно
при условии, что моляр постоянного давления теплоемкость (или удельная теплоемкость) Cп постоянно и что нет фаза перехода происходит в этом температурном интервале.
Аналогично при постоянном объеме изменение энтропии равно
где молярная теплоемкость постоянного объема Cv постоянна и нет изменения фазы.
При низких температурах, близких к абсолютному нулю, теплоемкость твердых тел быстро падает почти до нуля, поэтому предположение о постоянной теплоемкости неприменимо.[54]
Поскольку энтропия - это государственная функция, изменение энтропии любого процесса, в котором изменяются температура и объем, такое же, как для пути, разделенного на два этапа - нагрев при постоянном объеме и расширение при постоянной температуре. Для идеального газа полное изменение энтропии равно[55]
Точно так же, если температура и давление идеального газа изменяются,
Фазовые переходы
Обратимый фазовые переходы происходят при постоянной температуре и давлении. Обратимая теплота - это изменение энтальпии для перехода, а изменение энтропии - это изменение энтальпии, деленное на термодинамическую температуру.[56] Для слияния (таяние ) твердого вещества в жидкость при температуре плавления Тм, то энтропия плавления является
Аналогично для испарение жидкости в газ при температуре кипения Тб, то энтропия испарения является
Подходы к пониманию энтропии
В качестве фундаментального аспекта термодинамики и физики применимы несколько различных подходов к энтропии, помимо Клаузиуса и Больцмана.
Стандартные определения в учебниках
Ниже приводится список дополнительных определений энтропии из сборника учебников:
- мера рассредоточение энергии при определенной температуре.
- мера беспорядка во Вселенной или наличия в системе энергии для выполнения работы.[57]
- мера системы тепловая энергия на единицу температуры, недоступную для использования работай.[58]
В определении Больцмана энтропия - это мера количества возможных микроскопических состояний (или микросостояний) системы в термодинамическом равновесии. В соответствии с определением Больцмана второй закон термодинамики необходимо переформулировать так, чтобы энтропия со временем возрастала, хотя основной принцип остается прежним.
Порядок и беспорядок
Энтропия часто слабо связана с количеством порядок или же беспорядок, или из хаос, в термодинамическая система. Традиционное качественное описание энтропии заключается в том, что она относится к изменениям в статус-кво системы и является мерой «молекулярного беспорядка» и количества потерянной энергии при динамическом преобразовании энергии из одного состояния или формы в другое. В этом направлении несколько недавних авторов вывели точные формулы энтропии для учета и измерения беспорядка и порядка в атомных и молекулярных ансамблях.[59][60][61] Одна из более простых формул энтропийного порядка / беспорядка была получена в 1984 году физиком-термодинамиком Питером Ландсбергом на основе комбинации термодинамика и теория информации аргументы. Он утверждает, что когда в системе действуют ограничения, не позволяющие ей войти в одно или несколько возможных или разрешенных состояний, в отличие от ее запрещенных состояний, мера общего количества «беспорядка» в системе определяется выражением :[60][61]
Точно так же общая сумма «заказа» в системе определяется как:
В котором CD "беспорядочная" способность системы, которая представляет собой энтропию частей, содержащихся в разрешенном ансамбле, Cя "информационная" емкость системы, выражение, подобное выражению Шеннона. пропускная способность канала, и CО - это «порядковая» емкость системы.[59]
Рассеивание энергии
Понятие энтропии может быть описано качественно как мера рассеяния энергии при определенной температуре.[62] Подобные термины использовались с самого начала истории классическая термодинамика, а с развитием статистическая термодинамика и квантовая теория изменения энтропии были описаны в терминах смешивания или «распространения» полной энергии каждого компонента системы по ее конкретным квантованным уровням энергии.
Неясности в терминах беспорядок и хаос, которые обычно имеют значение, прямо противоположное равновесию, вносят свой вклад в широко распространенную путаницу и затрудняют понимание энтропии для большинства студентов.[63] Поскольку второй закон термодинамики показывает, в изолированная система внутренние части при различных температурах стремятся достичь единой однородной температуры и, таким образом, достичь равновесия. Недавно разработанный образовательный подход избегает двусмысленных терминов и описывает такое распространение энергии как рассеивание, которое приводит к потере дифференциалов, необходимых для работы, даже если общая энергия остается постоянной в соответствии с первый закон термодинамики[64] (сравните обсуждение в следующем разделе). Физико-химик Питер Аткинс например, ранее писавший о рассредоточении, ведущем к неупорядоченному состоянию, теперь пишет, что «спонтанные изменения всегда сопровождаются рассеянием энергии».[65]
Связь энтропии с энергией полезность
Следуя вышеизложенному, можно (в термическом контексте) рассматривать более низкую энтропию как индикатор или меру эффективность или же полезность определенного количества энергии.[66] Это связано с тем, что энергия, подаваемая при более высокой температуре (т.е. с низкой энтропией), имеет тенденцию быть более полезной, чем такое же количество энергии, доступной при более низкой температуре. Смешивание горячего пакета жидкости с холодной дает пакет промежуточной температуры, в котором общее увеличение энтропии представляет собой «потерю», которую невозможно возместить.
Таким образом, тот факт, что энтропия Вселенной неуклонно растет, означает, что ее общая энергия становится менее полезной: в конечном итоге это приводит к "тепловая смерть Вселенной."[67]
Энтропия и адиабатическая доступность
Определение энтропии полностью основано на соотношении адиабатическая доступность между состояниями равновесия был задан Э. Х. Либ и Дж. Ингвасон в 1999 году.[68] У этого подхода есть несколько предшественников, в том числе новаторская работа Константин Каратеодори с 1909 г.[69] и монография Р. Джайлза.[70] В постановке Либа и Ингвасона каждый начинает с выбора для единицы количества рассматриваемого вещества двух эталонных состояний и так что последний адиабатически доступен из первого, но не наоборот. Определение энтропии эталонных состояний равными 0 и 1 соответственно энтропии состояния определяется как наибольшее число такой, что адиабатически доступен из составного состояния, состоящего из количества в состоянии и дополнительная сумма, , в состоянии . Простой, но важный результат в рамках этой настройки заключается в том, что энтропия однозначно определяется, помимо выбора единицы и аддитивной константы для каждого химического элемента, следующими свойствами: она монотонна относительно отношения адиабатической доступности, аддитивности к композиту. системы, и обширные при масштабировании.
Энтропия в квантовой механике
В квантовая статистическая механика, концепция энтропии была развита Джон фон Нейман и обычно обозначается как "энтропия фон Неймана ",
где ρ - матрица плотности а Tr - это след оператор.
Это поддерживает принцип соответствия, потому что в классический предел, когда фазы между базисными состояниями, используемыми для классических вероятностей, являются чисто случайными, это выражение эквивалентно известному классическому определению энтропии,
т.е. в таком базисе матрица плотности диагональна.
Фон Нейман в своей работе создал строгую математическую основу для квантовой механики. Mathematische Grundlagen der Quantenmechanik. В этой работе он представил теорию измерения, в которой обычное понятие коллапс волновой функции описывается как необратимый процесс (так называемое фон Неймана или проективное измерение). Используя эту концепцию в сочетании с матрица плотности он распространил классическое понятие энтропии на квантовую область.
Теория информации
Разговор между Клод Шеннон и Джон фон Нейман относительно того, какое имя дать затухание в сигналах телефонной линии[71]
Если рассматривать с точки зрения теории информации, функция состояния энтропии - это просто количество информации (в смысле Шеннона), которая потребуется для определения полного микросостояния системы. Это не указано в макроскопическом описании.
В теория информации, энтропия - это мера количества информации, которая отсутствует до приема, и иногда ее называют Энтропия Шеннона.[72] Энтропия Шеннона - это широкое и общее понятие, используемое в теории информации, а также термодинамика. Первоначально он был разработан Клод Шеннон в 1948 г. для изучения количества информации в передаваемом сообщении. Однако определение информационной энтропии является довольно общим и выражается в терминах дискретного набора вероятностей. пя так что
В случае переданных сообщений эти вероятности представляли собой вероятности того, что конкретное сообщение было действительно передано, а энтропия системы сообщений была мерой среднего количества информации в сообщении. Для случая равных вероятностей (то есть каждое сообщение равновероятно) энтропия Шеннона (в битах) - это просто количество вопросов типа да / нет, необходимых для определения содержания сообщения.[22]
Вопрос о связи между информационной энтропией и термодинамической энтропией является дискуссионным. Хотя большинство авторов утверждают, что между ними существует связь,[73][74][75][76][77] некоторые утверждают, что они не имеют ничего общего друг с другом.[78]Выражения для двух энтропий аналогичны. Если W - это количество микросостояний, которые могут дать данное макросостояние, и каждое микросостояние имеет то же самое априори вероятность, то эта вероятность равна п = 1/W. Энтропия Шеннона (в нац ) является:
и если энтропия измеряется в единицах k на нат, тогда энтропия дается[79] к:
который является известным Формула энтропии Больцмана когда k - постоянная Больцмана, которую можно интерпретировать как термодинамическую энтропию на нат. Есть много способов продемонстрировать эквивалентность «информационной энтропии» и «энтропии физики», то есть эквивалентности «энтропии Шеннона» и «энтропии Больцмана». Тем не менее, некоторые авторы выступают за отказ от слова энтропия для ЧАС функция теории информации и использование другого термина Шеннона «неопределенность».[80]
Экспериментальное измерение энтропии
Энтропию вещества можно измерить, хотя и косвенным образом. При измерении используется определение температуры[81] с точки зрения энтропии, ограничивая энергообмен теплом ().
Полученное соотношение описывает, как изменяется энтропия когда небольшое количество энергии вводится в систему при определенной температуре.
Процесс измерения происходит следующим образом. Сначала образец вещества охлаждают как можно ближе к абсолютному нулю. При таких температурах энтропия приближается к нулю - из-за определения температуры. Затем в образец вводят небольшое количество тепла и регистрируют изменение температуры, пока температура не достигнет желаемого значения (обычно 25 ° C). Полученные данные позволяют пользователю интегрировать приведенное выше уравнение, получая абсолютное значение энтропии вещества при конечной температуре. Это значение энтропии называется калориметрической энтропией.[82]
Междисциплинарные приложения энтропии
Именно Рудольф Клаузиус ввел слово «энтропия» в свою статью, опубликованную в 1865 году.[83] Клаузиус изучал работы Сади Карно и лорда Кельвина и обнаружил, что неиспользуемая энергия увеличивается по мере прохождения пара от входа к выходу в паровой машине. Это открытие привело Клаузиуса к новому термодинамическое свойство то, что он назвал «энтропией». Слово происходит от греческого слова «энтропия», означающего преобразование. Слово «энтропия» было принято в английском языке в 1868 году. Хотя концепция энтропии изначально была термодинамической конструкцией, она была адаптирована в других областях исследования, включая теория информации, психодинамика, термоэкономика /экологическая экономика, и эволюция.[59][84][85][86][87]Например, недавно был предложен энтропийный аргумент для объяснения предпочтения пещерных пауков при выборе подходящего места для откладывания яиц.[88] При таком расширении полей / систем, к которым применим Второй закон термодинамики, значение слова энтропия также расширилась и основана на движущей энергии этой системы. Эта классификация дана в книге Сачидананды Кангови под названием «Закон беспорядка».[89] В этой книге эти системы также делятся на три категории, а именно: естественные, гибридные и созданные руками человека, в зависимости от степени контроля, который люди имеют в замедлении безжалостного марша энтропии, и шкалы времени каждой категории для достижения максимальной энтропии.
Концепции термодинамики и статистической механики
- Единица энтропии - не С.И. единица термодинамической энтропии, обычно обозначаемая как «e.u.» и равно одному калорийность на кельвин на моль, или 4,184 джоули на кельвин на моль.[90]
- Энтропия Гиббса - обычная статистическая механическая энтропия термодинамической системы.
- Энтропия Больцмана - тип энтропии Гиббса, который не учитывает внутренние статистические корреляции в общем распределении частиц.
- Энтропия Цаллиса - обобщение стандартной энтропии Больцмана – Гиббса.
- Стандартная молярная энтропия - содержание энтропии одного моля вещества в условиях стандартной температуры и давления.
- Остаточная энтропия - энтропия, возникающая после охлаждения вещества, произвольно близкого к абсолютный ноль.
- Энтропия смешения - изменение энтропии при двух разных химические субстанции или же составные части смешаны.
- Энтропия петли - энтропия, теряемая при сближении двух остатков полимера на заданном расстоянии.
- Конформационная энтропия - энтропия, связанная с физическим устройством полимер цепочка, предполагающая компактность или шаровидный состояние в растворе.
- Энтропическая сила - микроскопические силы или реакции, связанные с изменениями в организации системы, соображениями молекулярного трения и статистическими вариациями.
- Свободная энтропия - энтропийный термодинамический потенциал, аналогичный свободной энергии.
- Энтропический взрыв - взрыв, при котором реагенты сильно изменяются в объеме без выделения большого количества тепла.
- Изменение энтропии - изменение энтропии dS между двумя состояния равновесия дается теплопередачей dQrev разделенный на абсолютная температура Т из система в этом интервале.
- Энтропия Сакура – Тетрода - энтропия одноатомного классического идеального газа, определяемая из квантовых соображений.
Стрела времени
Энтропия - единственная величина в физических науках, которая, кажется, подразумевает определенное направление прогресса, иногда называемое стрела времени. Со временем второй закон термодинамики утверждает, что энтропия изолированная система никогда не уменьшается в больших системах в течение значительных периодов времени. Следовательно, с этой точки зрения, измерение энтропии в этих условиях считается часами.
Энтропия в последовательностях ДНК
Доказано, что энтропия полезна при анализе последовательностей ДНК. Было показано, что многие основанные на энтропии меры позволяют различать различные структурные области генома, различать кодирующие и некодирующие области ДНК, а также могут применяться для воссоздания эволюционных деревьев путем определения эволюционного расстояния между различными видами.[91]
Космология
Предполагая, что конечная вселенная является изолированной системой, второй закон термодинамики утверждает, что его общая энтропия постоянно увеличивается. С XIX века предполагалось, что Вселенной суждено тепловая смерть в котором все энергия в конечном итоге происходит однородное распределение тепловой энергии, так что больше нельзя извлекать работу из какого-либо источника.
Если можно считать, что энтропия Вселенной в целом возрастает, то - как Роджер Пенроуз указал - сила тяжести играет важную роль в увеличении, потому что гравитация заставляет дисперсное вещество накапливаться в звезды, которые в конечном итоге коллапсируют в черные дыры. Энтропия черной дыры пропорциональна площади поверхности черной дыры горизонт событий.[92][93][94] Якоб Бекенштейн и Стивен Хокинг показали, что черные дыры обладают максимально возможной энтропией любого объекта равного размера. Это делает их вероятными конечными точками всех процессов увеличения энтропии, если они являются полностью эффективными ловушками для вещества и энергии.[95] Однако утечка энергии из черных дыр может быть возможна из-за квантовой активности (см. Радиация Хокинга ).
Роль энтропии в космологии остается спорным вопросом, так как время Людвиг Больцманн. Недавняя работа поставила под сомнение гипотезу тепловой смерти и применимость любой простой термодинамической модели ко Вселенной в целом. Хотя энтропия действительно увеличивается в модели расширяющейся Вселенной, максимально возможная энтропия растет гораздо быстрее, перемещая Вселенную дальше от тепловой смерти со временем, а не ближе.[96][97][98] Это приводит к «энтропийной щели», отталкивающей систему от предполагаемого равновесия тепловой смерти.[99] Другие усложняющие факторы, такие как плотность энергии вакуума и макроскопические квант эффекты, трудно согласовать с термодинамическими моделями, что делает любые предсказания крупномасштабной термодинамики чрезвычайно трудными.[100]
Современные теории предполагают, что энтропийный разрыв был первоначально открыт раннее быстрое экспоненциальное расширение Вселенной.[101]
Экономика
Румынский американец экономист Николас Георгеску-Роген, а прародитель в экономика и основатель парадигмы из экологическая экономика, широко использовал понятие энтропии в его magnum opus на Закон энтропии и экономический процесс.[74] Благодаря работе Георгеску-Рогена законы термодинамики теперь образуют неотъемлемая часть школы экологической экономики.[102]:204f[103]:29–35 Хотя его работа была испорченный ошибками, полная глава по экономике Георгеску-Рогена была одобрительно включена в один элементарный учебник физики по историческому развитию термодинамики.[104]:95–112
В экономика, Работа Георгеску-Рогена породила термин "энтропийный пессимизм".[105]:116 С 1990-х годов ведущий экологический экономист и теоретик устойчивого состояния Герман Дейли - ученик Георгеску-Рогена - был самым влиятельным сторонником позиции энтропийного пессимизма в экономической профессии.[106]:545f[107]
Герменевтика
В Герменевтика, Арианна Беатрис Фаббрикаторе использовала термин энтропия, опираясь на работы Умберто Эко,[108] определить и оценить потерю смысла между словесным описанием танца и хореотекстом (движущийся шелк, задействованный танцором, когда он приводит в действие хореографическое письмо)[109] генерируется операциями межсемиотического перевода.[110][111]
Это использование связано с понятиями логотекста и хореотекста. При переходе от логотекста к хореотексту можно выделить две типологии энтропии: первая, называемая «естественной», связана с уникальностью перформативного акта и его эфемерностью. Вторая причина связана с более или менее важными "пустотами" в логотипе текста (т.е. словесный текст, отражающий танцевальное действие[112]).
Смотрите также
- Автокаталитические реакции и создание заказов
- Броуновская трещотка
- Неравенство Клаузиуса-Дюгема
- Энтропия конфигурации
- Функция отправления
- Энтальпия
- Энтропическая сила
- Энтропийная ценность под угрозой
- Энтропия (теория информации)
- Энтропия (вычисления)
- Энтропия (статистическая термодинамика)
- Энтропия и жизнь
- Энтропия (порядок и беспорядок)
- Скорость энтропии
- Производство энтропии
- Экстропия
- Геометрическое разочарование
- Гармоническая энтропия
- Тепловая смерть вселенной
- Инфо-метрики
- Законы термодинамики
- Функция кратности
- Негэнтропия (отрицательная энтропия)
- Порядки величины (энтропия)
- Фазовое пространство
- Принцип максимальной энтропии
- Формула Стирлинга
- Термодинамические базы данных чистых веществ
- Термодинамический потенциал
- Термодинамическое равновесие
- Вейвлет энтропия
Примечания
- ^ Точки представляют собой производные величин по времени.
Рекомендации
- ^ Лигроне, Роберто (2019). «Глоссарий». Биологические инновации, построившие мир: путешествие продолжительностью четыре миллиарда лет по истории жизни и Земли. Энтропия. Springer. п. 478. ISBN 978-3030160562. Получено 29 августа 2019.
- ^ Ритман, Эдвард А .; Тушинский, Джек А. (2017). "Термодинамика и состояние покоя рака: взгляд в будущее". Ин Ван, Юйчжуо; Crea, Francesco (ред.). Покой и рецидив опухоли (открытие и разработка противораковых препаратов). Введение: энтропия и информация. Humana Press. п. 63. ISBN 978-3319592404. Получено 29 августа 2019.
- ^ "Карно, Сади (1796–1832)". Wolfram Research. 2007 г.. Получено 24 февраля 2010.
- ^ Маккаллох, Ричард, С. (1876). Трактат по механической теории тепла и ее приложениям к паровому двигателю и т. Д.. Д. Ван Ностранд.
- ^ а б Клаузиус, Рудольф (1850). "Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbstableiten lassen". Annalen der Physik. 155 (3): 368–397. Bibcode:1850АнП ... 155..368С. Дои:10.1002 / andp.18501550306. HDL:2027 / uc1. $ B242250. [О движущей силе тепла и о законах, которые могут быть выведены из нее для теории тепла]: Поггендорф. Annalen der Physik und Chemie
- ^ а б Гиллиспи, Чарльз Коулстон (1960). Грань объективности: очерк истории научных идей. Издательство Принстонского университета. п.399. ISBN 0-691-02350-6.
- ^ Клаузиус, Рудольф (1865). "Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der Mechanischen Wärmetheorie (Vorgetragen in der naturforsch. Gesellschaft zu Zürich den 24. апреля 1865 г.)". Annalen der Physik und Chemie. 125 (7): 353–400. Bibcode:1865AnP ... 201..353C. Дои:10.1002 / andp.18652010702."Сучт человек фюр S einen bezeichnenden Namen, so könnte man, ähnlich wie von der Gröſse U gesagt ist, sie sey der Wärme- und Werkinhalt des Körpers, von der Gröſse S sagen, sie sey der Verwandlungsinhalt des Körpers. Da ich es aber für besser halte, die Namen derartiger für die Wissenschaft wichtiger Gröſsen aus den alten Sprachen zu entnehmen, damit sie unverändert in allen neuen Sprachen angewandt werden können, so schlage ö vor, die S nach dem griechischen Worte ἡ τροπὴ, die Verwandlung, die Энтропия des Körpers zu nennen. Das Wort Энтропия habei ich absichtlich dem Worte Energie möglichst ähnlich gebildet, denn die beiden Gröſsen, welche durch diese Worte benannt werden sollen, sind ihren Physikalischen Bedeutungen nach einander so nahe verwandt, daſs eine gewisse Gleichartigkeit in der benweckmänung.
- ^ Научные статьи Дж. Уилларда Гиббса в двух томах. 1. Лонгманс, Грин и Ко. 1906. стр. 11. Получено 26 февраля 2011.
- ^ Дж. А. Макговерн,«2.5 Энтропия». Архивировано из оригинал 23 сентября 2012 г.. Получено 5 февраля 2013.
- ^ «6.5 Необратимость, изменения энтропии и Потерянная работа". web.mit.edu. Получено 21 мая 2016.
- ^ Ниже, Стивен. "Что такое энтропия?". www.chem1.com. Получено 21 мая 2016.
- ^ Лавенда, Бернард Х. (2010). «2.3.4». Новый взгляд на термодинамику (Online-Ausg. Ed.). Нью-Йорк: Спрингер. ISBN 978-1-4419-1430-9.
- ^ Карно, Сади Карно (1986). Фокс, Роберт (ред.). Размышления о движущей силе огня. Нью-Йорк: Лилиан Барбер Пресс. стр.26. ISBN 978-0-936508-16-0.
- ^ Трусделл, К. (1980). Трагикомическая история термодинамики 1822–1854 гг.. Нью-Йорк: Спрингер. стр.78 –85. ISBN 978-0-387-90403-0.
- ^ Клерк Максвел, Джеймс (2001). Пешич, Питер (ред.). Теория тепла. Минеола: Dover Publications. С. 115–158. ISBN 978-0-486-41735-6.
- ^ Рудольф Клаузиус (1867). Механическая теория тепла: ее приложения к паровому двигателю и физическим свойствам тел. Дж. Ван Ворст. п. 28. ISBN 978-1-4981-6733-8.
- ^ Аткинс, Питер; Хулио де Паула (2006). Физическая химия, 8-е изд.. Издательство Оксфордского университета. п. 79. ISBN 978-0-19-870072-2.
- ^ Энгель, Томас; Филип Рид (2006). Физическая химия. Пирсон Бенджамин Каммингс. п. 86. ISBN 978-0-8053-3842-3.
- ^ а б c Ликер, Марк Д. (2004). Макгроу-Хилл краткая энциклопедия химии. Нью-Йорк: McGraw-Hill Professional. ISBN 978-0-07-143953-4.
- ^ а б Сетна, Джеймс П. (2006). Статистическая механика: энтропия, параметры порядка и сложность ([Online-Ausg.] Ред.). Оксфорд: Издательство Оксфордского университета. п.78. ISBN 978-0-19-856677-9.
- ^ Кларк, Джон О. (2004). Основной научный словарь. Нью-Йорк: Barnes & Noble. ISBN 978-0-7607-4616-5.
- ^ а б Фригг, Р. и Верндль, К. «Энтропия - руководство для недоумевших». В Вероятности в физике; Бейсбарт К. и Хартманн, С. Эдс; Oxford University Press, Оксфорд, 2010 г.
- ^ Шредер, Даниэль В. (2000). Введение в теплофизику. Сан-Франциско, Калифорния: Эддисон Уэсли. п.57. ISBN 978-0-201-38027-9.
- ^ Аллен, Майкл П .; Тилдесли, Доминик Дж. (23 ноября 2017 г.). «Компьютерное моделирование жидкостей». Оксфордская стипендия онлайн. Дои:10.1093 / oso / 9780198803195.001.0001. ISBN 9780198803195.
- ^ Розенфельд, Яаков (1 июня 1977 г.). «Связь транспортных коэффициентов с внутренней энтропией простых систем». Физический обзор A. 15 (6): 2545–2549. Bibcode:1977ПхРвА..15.2545Р. Дои:10.1103 / PhysRevA.15.2545. ISSN 0556-2791.
- ^ Дайр, Джепп К. (2018). «Перспектива: масштабирование избыточной энтропии». Журнал химической физики. 149 (21): 210901. Дои:10.1063/1.5055064. ISSN 0021-9606. PMID 30525736.
- ^ Белл, Ян Х. (2019). «Исследование связи между остаточной энтропией и вязкостью молекулярных жидкостей и модельными потенциалами». Труды Национальной академии наук. 116 (10): 4070–4079. Дои:10.1073 / pnas.1815943116. ISSN 0027-8424. ЧВК 6410835. PMID 30770449.
- ^ Белл, Ян Х .; Dyre, Jeppe C .; Ингебригцен, Тронд С. (2020). «Масштаб избыточной энтропии в переохлажденных бинарных смесях». Nature Communications. 11 (1): 4300. Дои:10.1038 / s41467-020-17948-1. ISSN 2041-1723. ЧВК 7453028. PMID 32855393.
- ^ "EntropyOrderParametersComplexity.pdf www.physics.cornell.edu" (PDF). Получено 17 августа 2012.
- ^ Джейнс, Э. (1992). Смит, C.R; Эриксон, Г.Дж .; Neudorfer, P.O. (ред.). «Парадокс Гиббса», [in] Максимальная энтропия и байесовские методы. (PDF). Kluwer Academic: Дордрехт. стр. 1–22. Получено 17 августа 2012.
- ^ а б Сэндлер, Стэнли И. (2006). Химическая, биохимическая и инженерная термодинамика (4-е изд.). Нью-Йорк: Джон Вили и сыновья. п.91. ISBN 978-0-471-66174-0.
- ^ Саймон, Дональд А. МакКуорри; Джон Д. (1997). Физическая химия: молекулярный подход (Ред. Ред.). Саусалито, Калифорния: Univ. Научные книги. п. 817. ISBN 978-0-935702-99-6.
- ^ Хейни, Дональд, Т. (2001). Биологическая термодинамика. Издательство Кембриджского университета. ISBN 978-0-521-79165-6.
- ^ Дейнтит, Джон (2005). Научный словарь (5-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-280641-3.
- ^ де Росне, Джоэл (1979). Макроскоп - новый взгляд на мир (написано биохимиком, получившим образование в Массачусетском технологическом институте). Harper & Row, Publishers. ISBN 978-0-06-011029-1.
- ^ Макговерн, Дж. А. «Тепловые мощности». Архивировано из оригинал 19 августа 2012 г.. Получено 27 января 2013.
- ^ Бен-Наим, Арье (21 сентября 2007 г.). «О так называемом парадоксе Гиббса и о реальном парадоксе» (PDF). Энтропия. 9 (3): 132–136. Bibcode:2007Entrp ... 9..132B. Дои:10.3390 / e9030133.
- ^ Каллен, Герберт (2001). Термодинамика и введение в термостатистику (2-е изд.). Джон Уайли и сыновья. ISBN 978-0-471-86256-7.
- ^ Гао, Сян; Галликкио, Эмилио; Ройтберг, Адриан (2019). «Обобщенное распределение Больцмана - единственное распределение, в котором энтропия Гиббса-Шеннона равна термодинамической энтропии». Журнал химической физики. 151 (3): 034113. arXiv:1903.02121. Bibcode:2019JChPh.151c4113G. Дои:10.1063/1.5111333. PMID 31325924. S2CID 118981017.
- ^ Дейнтит, Джон (2005). Оксфордский физический словарь. Издательство Оксфордского университета. ISBN 978-0-19-280628-4.
- ^ Саха, Арнаб; Лахири, Сураб; Джаяннавар, А. М. (2009). «Теоремы производства энтропии и некоторые следствия». Физический обзор E. 80 (1): 1–10. arXiv:0903.4147. Bibcode:2009PhRvE..80a1117S. Дои:10.1103 / PhysRevE.80.011117. PMID 19658663. S2CID 22204063.
- ^ Мартюшев, Л. М .; Селезнев, В. Д. (2014). «Ограничения принципа максимального производства энтропии». Physica A: Статистическая механика и ее приложения. 410: 17–21. arXiv:1311.2068. Bibcode:2014PhyA..410 ... 17M. Дои:10.1016 / j.physa.2014.05.014. S2CID 119224112.
- ^ Зиглер, Х. (1983). Введение в термомеханику. Северная Голландия, Амстердам.
- ^ Онзагер, Ларс (1931). «Взаимоотношения в необратимых процессах». Phys. Rev. 37 (4): 405. Bibcode:1931ПхРв ... 37..405О. Дои:10.1103 / PhysRev.37.405.
- ^ Kleidon, A .; и другие. (2005). Неравновесная термодинамика и производство энтропии. Гейдельберг: Springer.
- ^ Белкин Андрей; и другие. (2015). «Самособирающиеся извивающиеся наноструктуры и принцип максимального производства энтропии». Научные отчеты. 5: 8323. Bibcode:2015НатСР ... 5Э8323Б. Дои:10.1038 / srep08323. ЧВК 4321171. PMID 25662746.
- ^ а б Мур, Дж. В .; К. Л. Станистский; П. К. Юрс (2005). Химия, Молекулярная наука. Брукс Коул. ISBN 978-0-534-42201-1.
- ^ Юнгерманн, А.Х. (2006). «Энтропия и модель полки: квантово-физический подход к физическому свойству». Журнал химического образования. 83 (11): 1686–1694. Bibcode:2006JChEd..83.1686J. Дои:10.1021 / ed083p1686. S2CID 18081336.
- ^ Левин, И. Н. (2002). Физическая химия, 5-е изд.. Макгроу-Хилл. ISBN 978-0-07-231808-1.
- ^ Покойный лауреат Нобелевской премии Макс Борн (8 августа 2015 г.). Естественная философия причины и случая. BiblioLife.С. 44, 146–147. ISBN 978-1-298-49740-6.
- ^ Хаазе, Р. (1971). Термодинамика. Нью-Йорк: Academic Press. С. 1–97. ISBN 978-0-12-245601-5.
- ^ Сэндлер, Стэнли, И. (1989). Химическая и инженерная термодинамика. Джон Вили и сыновья. ISBN 978-0-471-83050-4.
- ^ "GRC.nasa.gov". GRC.nasa.gov. 27 марта 2000 г. Архивировано с оригинал 21 августа 2011 г.. Получено 17 августа 2012.
- ^ Франзен, Стефан. «Третий закон» (PDF). ncsu.edu. Архивировано из оригинал (PDF) 9 июля 2017 г.
- ^ "GRC.nasa.gov". GRC.nasa.gov. 11 июля 2008 г.. Получено 17 августа 2012.
- ^ Старзак, Майкл Э. (2010). «Фазовые равновесия и коллигативные свойства». Энергия и энтропия: равновесие в стационарных состояниях. Springer Science + Business Media. С. 138–140. ISBN 978-1489983671. Получено 5 сентября 2019.
- ^ Гриббин, Джон (1999). Гриббин, Мэри (ред.). Q означает квант: энциклопедия физики элементарных частиц. Нью-Йорк: Свободная пресса. ISBN 978-0-684-85578-3.
- ^ «Энтропия: определение и уравнение». Британская энциклопедия. Получено 22 мая 2016.
- ^ а б c Брукс, Дэниел Р .; Уайли, Э. О. (1988). Эволюция как энтропия: к единой теории биологии (2-е изд.). Чикаго [и др.]: Издательство Чикагского университета. ISBN 978-0-226-07574-7.
- ^ а б Ландсберг, П. (1984). «Всегда ли равновесие является максимумом энтропии?». J. Stat. Физика. 35 (1–2): 159–169. Bibcode:1984JSP .... 35..159л. Дои:10.1007 / bf01017372. S2CID 122424225.
- ^ а б Ландсберг, П. (1984). «Могут ли энтропия и« порядок »расти вместе?». Письма по физике. 102A (4): 171–173. Bibcode:1984ФЛА..102..171Л. Дои:10.1016/0375-9601(84)90934-4.
- ^ Ламберт, Фрэнк Л. «Студенческий подход ко второму закону и энтропии». entropysite.oxy.edu. Архивировано из оригинал 17 июля 2009 г.. Получено 22 мая 2016.
- ^ Watson, J.R .; Карсон, Э.М. (май 2002 г.). «Понимание студентами энтропии и свободной энергии Гиббса» (PDF). Университетское химическое образование. 6 (1): 4. ISSN 1369-5614.
- ^ Ламберт, Фрэнк Л. (февраль 2002 г.). «Беспорядок - треснувший костыль для поддержки энтропийных дискуссий». Журнал химического образования. 79 (2): 187. Bibcode:2002JChEd..79..187L. Дои:10.1021 / ed079p187. S2CID 97102995.
- ^ Аткинс, Питер (1984). Второй закон. Научная американская библиотека. ISBN 978-0-7167-5004-8.
- ^ Сандра Саари (23 февраля 1993 г.). "Книжное обозрение" Научного сборника"". Khaleej Times. ОАЭ: Galadari Press: xi.
- ^ Lathia, R; Agrawal, T; Parmar, V; Добария, К; Патель, А (20 октября 2015 г.). «Тепловая смерть (Конечная судьба Вселенной)». Дои:10.13140 / rg.2.1.4158.2485. Цитировать журнал требует
| журнал =(помощь) - ^ Lieb, Elliott H .; Ингвасон, Якоб (март 1999 г.). «Физико-математические науки второго начала термодинамики». Отчеты по физике. 310 (1): 1–96. arXiv:cond-mat / 9708200. Bibcode:1999ФР ... 310 .... 1л. Дои:10.1016 / S0370-1573 (98) 00082-9. S2CID 119620408.
- ^ Каратеодори, К. (сентябрь 1909 г.). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen (на немецком). 67 (3): 355–386. Дои:10.1007 / BF01450409. S2CID 118230148.
- ^ Р. Джайлз (2016). Математические основы термодинамики: Международная серия монографий по чистой и прикладной математике. Elsevier Science. ISBN 978-1-4831-8491-3.
- ^ Tribus, M .; Макирвайн, Э. К. (1971). «Энергия и информация». Scientific American. 224: 178–184.
- ^ Балиан, Роджер (2004). «Энтропия, концепция Protean». В Далибарде, Жан (ред.). Семинар Пуанкаре 2003: конденсация Бозе-Эйнштейна - энтропия. Базель: Биркхойзер. С. 119–144. ISBN 978-3-7643-7116-6.
- ^ Бриллюэн, Леон (1956). Наука и теория информации. ISBN 978-0-486-43918-1.
- ^ а б Джорджеску-Роэген, Николас (1971). Закон энтропии и экономический процесс. Издательство Гарвардского университета. ISBN 978-0-674-25781-8.
- ^ Чен, Цзин (2005). Физические основы экономики - аналитическая термодинамическая теория. World Scientific. ISBN 978-981-256-323-1.
- ^ Калинин, М.И.; Кононогов, С.А. (2005). «Постоянная Больцмана». Методы измерения. 48 (7): 632–636. Дои:10.1007 / s11018-005-0195-9. S2CID 118726162.
- ^ Бен-Наим, Арье (2008). Энтропия демистифицировала второй закон, сведенный к простому здравому смыслу (Расширенная ред.). Сингапур: World Scientific. ISBN 9789812832269.
- ^ Валлино, Джозеф Дж .; Алгар, Кристофер К .; Гонсалес, Нурия Фернандес; Хубер, Джули А. (2013). «Использование оптимального управления удаляющимся горизонтом для решения основанных на MaxEP (максимальное производство энтропии) проблем биогеохимии». В Dewar, Roderick C .; Lineweaver, Charles H .; Нивен, Роберт К .; Регенауэр-Либ, Клаус (ред.). За пределами второго закона: производство энтропии и неравновесные системы. Живые системы как катализаторы. Springer. п. 340. ISBN 978-3642401534. Получено 31 августа 2019.
Страница с чернилами формирует шаблон с информацией → энтропия страницы <страница сравнения с рандомизированными буквами. Пониженная энтропия тривиальна по сравнению с энтропией на бумаге с чернилами. Если бумага сгорела, в термодинамическом контексте вряд ли имеет значение, содержит ли текст смысл жизни или только треп.
- ^ "Эдвин Т. Джейнс - Библиография". Bayes.wustl.edu. 2 марта 1998 г.. Получено 6 декабря 2009.
- ^ Шнайдер, Том, система DELILA (язык библиотеки дезоксирибонуклеиновой кислоты), (Теоретический анализ информации сайтов связывания), Лаборатория математической биологии, Национальный институт рака, Фредерик, доктор медицины
- ^ Шредер, Даниэль В. (2000). Введение в теплофизику ([Nachdr.] Ред.). Сан-Франциско, Калифорния [u.a.]: Эддисон Уэсли. п.88. ISBN 978-0-201-38027-9.
- ^ «Измерение энтропии». www.chem.wisc.edu.
- ^ 2. Клаузиус, Рудольф, «Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der Mechanischen Wärmetheorie», Annalen der Physik, 125 (7): 353–400, 1865.
- ^ Эйвери, Джон (2003). Теория информации и эволюция. World Scientific. ISBN 978-981-238-399-0.
- ^ Йоки, Хуберт, П. (2005). Теория информации, эволюция и происхождение жизни. Издательство Кембриджского университета. ISBN 978-0-521-80293-2.
- ^ Кьяваццо, Элиодоро; Фазано, Маттео; Асинари, Пьетро (2013). «Вывод аналитических термодинамических моделей для биологических сетей» (PDF). Physica A: Статистическая механика и ее приложения. 392 (5): 1122–1132. Bibcode:2013PhyA..392.1122C. Дои:10.1016 / j.physa.2012.11.030.
- ^ Чен, Цзин (2015). Единство науки и экономики: новый фундамент экономической теории. https://www.springer.com/us/book/9781493934645: Springer.CS1 maint: location (связь)
- ^ Кьяваццо, Элиодоро; Исайя, Марко; Маммола, Стефано; Лепоре, Эмилиано; Вентола, Луиджи; Асинари, Пьетро; Пуньо, Никола Мария (2015). «Пещерные пауки выбирают оптимальные факторы окружающей среды относительно генерируемой энтропии при закладке кокона». Научные отчеты. 5: 7611. Bibcode:2015НатСР ... 5Э7611С. Дои:10.1038 / srep07611. ЧВК 5154591. PMID 25556697.
- ^ Сачидананда Кангови, «Закон беспорядка», ISBN 9798677301285, Amazon Publishing, 2020 г.
- ^ ИЮПАК, Сборник химической терминологии, 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) "Единица энтропии ". Дои:10.1351 / goldbook.E02151
- ^ Танос, Димитриос; Ли, Вентянь; Провата, Астеро (1 марта 2018 г.). «Энтропические колебания последовательностей ДНК». Physica A: Статистическая механика и ее приложения. 493: 444–457. Bibcode:2018PhyA..493..444T. Дои:10.1016 / j.physa.2017.11.119. ISSN 0378-4371.
- ^ фон Байер, Кристиан, Х. (2003). Информация - новый язык науки. Издательство Гарвардского университета. ISBN 978-0-674-01387-2.
- ^ Средницкий М. (август 1993 г.). «Энтропия и площадь». Phys. Rev. Lett. 71 (5): 666–669. arXiv:hep-th / 9303048. Bibcode:1993ПхРвЛ..71..666С. Дои:10.1103 / PhysRevLett.71.666. PMID 10055336. S2CID 9329564.
- ^ Callaway DJE (Апрель 1996 г.). «Поверхностное натяжение, гидрофобность и черные дыры: энтропийная связь». Phys. Ред. E. 53 (4): 3738–3744. arXiv:cond-mat / 9601111. Bibcode:1996PhRvE..53.3738C. Дои:10.1103 / PhysRevE.53.3738. PMID 9964684. S2CID 7115890.
- ^ Sarkar, T.K .; Салазар-Пальма, М .; Моколе, Эрик Л. (2008). «Взгляд на концепцию пропускной способности канала с точки зрения Максвелла». Физика многоантенных систем и широкополосная обработка данных. Вайли. п. 162. ISBN 978-0470190401. Получено 31 августа 2019.
- ^ Лайзер, Дэвид (1988). Рост порядка во Вселенной. MIT Press.
- ^ Chaisson, Эрик Дж. (2001). Космическая эволюция: рост сложности в природе. Издательство Гарвардского университета. ISBN 978-0-674-00342-2.
- ^ Lineweaver, Charles H .; Дэвис, Пол С. В .; Рус, Майкл, ред. (2013). Сложность и стрела времени. Издательство Кембриджского университета. ISBN 978-1-107-02725-1.
- ^ Стенгер, Виктор Дж. (2007). Бог: несостоятельная гипотеза. Книги Прометея. ISBN 978-1-59102-481-1.
- ^ Бенджамин Гал-Ор (1987). Космология, физика и философия. Springer Verlag. ISBN 978-0-387-96526-0.
- ^ Альбрехт, Андреас (2004). «Космическая инфляция и стрела времени» (PDF). В Барроу, Джон Д.; Дэвис, Пол К.; Харпер, Чарльз Л. мл. (Ред.). Наука и высшая реальность: от кванта к космосу. Кембридж, Великобритания: Издательство Кембриджского университета. arXiv:astro-ph / 0210527. Bibcode:2002astro.ph.10527A. Получено 28 июн 2017 (в честь 90-летия Джона Уиллера)
- ^ Кливленд, Катлер Дж.; Рут, Матиас (1997). «Когда, где и насколько биофизические ограничения сдерживают экономический процесс? Обзор вклада Николаса Георгеску-Рогена в экологическую экономику». Экологическая экономика. Амстердам: Эльзевир. 22 (3): 203–223. Дои:10.1016 / s0921-8009 (97) 00079-7.
- ^ Дали, Герман Э.; Фарли, Джошуа (2011). Экологическая экономика. Принципы и применение (PDF содержит полную книгу) (2-е изд.). Вашингтон: Island Press. ISBN 978-1-59726-681-9.
- ^ Шмитц, Джон Э.Дж. (2007). Второй закон жизни: энергия, технологии и будущее Земли, каким мы его знаем (Ссылка на научный блог автора, основанный на его учебнике). Норвич: Издательство Уильям Эндрю. ISBN 978-0-8155-1537-1.
- ^ Эйрес, Роберт У. (2007). «О практических пределах замены» (PDF). Экологическая экономика. Амстердам: Эльзевир. 61: 115–128. Дои:10.1016 / j.ecolecon.2006.02.011.
- ^ Кершнер, Кристиан (2010). «Экономический спад против устойчивой экономики» (PDF). Журнал чистого производства. Амстердам: Эльзевир. 18 (6): 544–551. Дои:10.1016 / j.jclepro.2009.10.019.
- ^ Дейли, Герман Э. (2015). «Экономика для полноценного мира». Scientific American. 293 (3): 100–7. Дои:10.1038 / scientificamerican0905-100. PMID 16121860. S2CID 13441670. Получено 23 ноября 2016.
- ^ Умберто Эко, Opera aperta. Forma e indeterminazione nelle poetiche contemporanee, Bompiani 2013
- ^ Арианна Беатрис Фаббрикаторе. (2017). La Querelle des Pantomimes. Танец, культура и общество в Европе люмьер. Ренн: Press Universitaires de Rennes.
- ^ Арианна Беатрис Фаббрикаторе. (2018). L'action dans le texte. Pour une Approche herméneutique du Trattato teorico-prattico di Ballo (1779) де Ж. Магри. [Ресурс ARDP 2015], Pantin, CN D.
- ^ "HDDanse 272". Гипотезы.
- ^ "Laction dans le texte CND fabbricatore" (PDF). Гипотезы. Март 2019. С. 1–115.
дальнейшее чтение
- Адам, Герхард; Отто Хиттмайр (1992). Wärmetheorie. Vieweg, Брауншвейг. ISBN 978-3-528-33311-9.
- Аткинс, Питер; Хулио де Паула (2006). Физическая химия (8-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-870072-2.
- Байерлейн, Ральф (2003). Теплофизика. Издательство Кембриджского университета. ISBN 978-0-521-65838-6.
- Бен-Наим, Арие (2007). Демистификация энтропии. World Scientific. ISBN 978-981-270-055-1.
- Каллен, Герберт, Б. (2001). Термодинамика и введение в термостатистику (2-е изд.). Джон Уайли и сыновья. ISBN 978-0-471-86256-7.
- Чанг, Раймонд (1998). Химия (6-е изд.). Нью-Йорк: Макгроу Хилл. ISBN 978-0-07-115221-1.
- Катнелл, Джон, Д .; Джонсон, Кеннет, Дж. (1998). Физика (4-е изд.). John Wiley and Sons, Inc. ISBN 978-0-471-19113-1.
- Дагдейл, Дж. С. (1996). Энтропия и ее физический смысл (2-е изд.). Тейлор и Фрэнсис (Великобритания); CRC (США). ISBN 978-0-7484-0569-5.
- Ферми, Энрико (1937). Термодинамика. Прентис Холл. ISBN 978-0-486-60361-2.
- Гольдштейн, Мартин; Инге, Ф (1993). Холодильник и Вселенная. Издательство Гарвардского университета. ISBN 978-0-674-75325-9.
- Gyftopoulos, E.P .; Г.П. Беретта (2010). Термодинамика. Основы и приложения. Дувр. ISBN 978-0-486-43932-7.
- Haddad, Wassim M .; Челлабоина, Виджай Сехар; Нерсесов, Сергей Г. (2005). Термодинамика - подход динамических систем. Princeton University Press. ISBN 978-0-691-12327-1.
- Джонсон, Эрик (2018). Беспокойство и уравнение: понимание энтропии Больцмана. MIT Press. ISBN 978-0-262-03861-4.
- Кремер, Герберт; Чарльз Киттель (1980). Теплофизика (2-е изд.). Компания W.H. Freeman. ISBN 978-0-7167-1088-2.
- Lambert, Frank L .; entropysite.oxy.edu
- Мюллер-Кирстен, Харальд Дж. В. (2013). Основы статистической физики (2-е изд.). Сингапур: World Scientific. ISBN 978-981-4449-53-3.
- Пенроуз, Роджер (2005). Дорога к реальности: полное руководство по законам Вселенной. Нью-Йорк: А. А. Кнопф. ISBN 978-0-679-45443-4.
- Рейф Ф. (1965). Основы статистической и теплофизики. Макгроу-Хилл. ISBN 978-0-07-051800-1.
- Шредер, Даниэль В. (2000). Введение в теплофизику. Нью-Йорк: Эддисон Уэсли Лонгман. ISBN 978-0-201-38027-9.
- Серуэй, Раймонд, А. (1992). Физика для ученых и инженеров. Сондерс Золотая серия Subburst. ISBN 978-0-03-096026-0.
- Спиракс-Сарко Лимитед, Энтропия - базовое понимание Праймер по таблицам энтропии для паровой техники
- vonBaeyer; Ганс Кристиан (1998). Демон Максвелла: почему рассеивается тепло и проходит время. Случайный дом. ISBN 978-0-679-43342-2.
внешняя ссылка
- Энтропия и второй закон термодинамики - лекция по физике A-level с подробным выводом энтропии на основе цикла Карно
- Khan Academy: энтропийные лекции, часть Плейлист по химии
- Второй закон термодинамики и энтропии - Лекция Йельского университета в OYC, часть курса "Основы физики I" (PHYS 200)
- Энтропия и неравенство Клаузиуса Лекция MIT OCW, часть 5.60 Термодинамика и кинетика, весна 2008 г.
- Открытие энтропии пользователя Адам Шульман. Часовое видео, январь 2013 г.
- Мориарти, Филипп; Меррифилд, Майкл (2009). «S Энтропия». Шестьдесят символов. Брэди Харан для Ноттингемский университет.
- "Энтропия" в Scholarpedia































![{displaystyle S = -k_ {mathrm {B}} имя оператора {E} [log p]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d15ce6116ba3b285454736f8d435bf4258f652f0)