Логарифмическая шкала - Logarithmic scale

А логарифмическая шкала (или шкала журнала) - это способ компактного отображения числовых данных в очень широком диапазоне значений - обычно самые большие числа в данных в сотни или даже тысячи раз больше, чем самые маленькие числа. Такой масштаб является нелинейный: числа 10 и 20, а также 60 и 70 не находятся на одинаковом расстоянии в логарифмической шкале. Напротив, числа 10 и 100, 60 и 600 расположены на одинаковом расстоянии. Таким образом, перемещение единицы расстояния по шкале означает, что число было изменено. умноженный на 10 (или другой фиксированный коэффициент). Часто экспоненциальный рост кривые отображаются в логарифмическом масштабе, в противном случае они увеличивались бы слишком быстро, чтобы поместиться в небольшой график. Еще один способ подумать об этом: количество цифры данных растет с постоянной скоростью. Например, числа 10, 100, 1000 и 10000 равномерно распределены по логарифмической шкале, поскольку их количество цифр увеличивается на 1 каждый раз: 2, 3, 4 и 5 цифр. Таким образом, добавляя две цифры умножается количество, измеренное по логарифмической шкале с коэффициентом 100.

Логарифмическая шкала от 0,1 до 100

График количества хостов в Интернете с течением времени, показанный в логарифмической шкале

Общее использование

Маркировка на правила слайдов расположены в логарифмической шкале для умножения или деления чисел путем добавления или вычитания длин на шкалах.

Две логарифмические шкалы логарифмической линейки

Ниже приведены примеры обычно используемых логарифмических шкал, где большее количество приводит к более высокому значению:

Шкала звездных величин Рихтера и шкала моментной магнитуды (MMS) для силы землетрясения и движение в Земля

Логарифмическая шкала позволяет легко сравнивать значения, охватывающие большой диапазон, например, на этой карте.
Уровень звука, с единицами децибел
Непер для величин амплитуды, поля и мощности
Уровень частоты, с единицами цент, второстепенная секунда, основная секунда, и октава для относительной высоты нот в Музыка
Logit для шансы в статистика
Палермская шкала опасности технических воздействий
Логарифмическая шкала времени
Подсчет f-стопы для соотношений фотографическая экспозиция
В правило девяток используется для низкого рейтинга вероятности
Энтропия в термодинамика
Информация в теория информации
Кривые гранулометрического состава почвы

Ниже приведены примеры часто используемых логарифмических шкал, где большее количество приводит к более низкому (или отрицательному) значению:

pH для кислотности
Шкала звездной величины для яркости звезды
Шкала Крамбейна для размер частицы в геология
Абсорбция света прозрачными образцами

Некоторые из наших чувства работают логарифмически (Закон Вебера – Фехнера ), что делает особенно подходящими логарифмические шкалы для этих входных величин. В частности, наше чувство слушание воспринимает равные отношения частот как равные различия в высоте тона. Кроме того, исследования маленьких детей в изолированном племени показали, что логарифмические шкалы являются наиболее естественным отображением чисел в некоторых культурах.^[1] Его также можно использовать для географических целей, например, для измерения скорость землетрясений.

Графическое представление

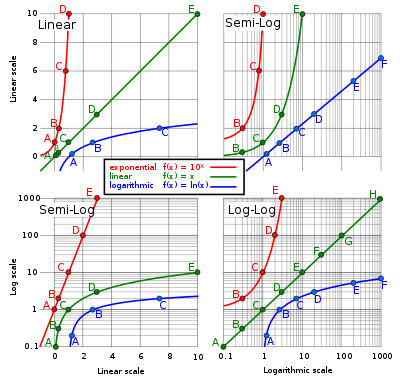
Различные масштабы: лин – лин, lin – log, log – lin, и журнал – журнал. Построенные графики: у = 10^Икс (красный), у = Икс (зеленый), у = журнал_е(Икс) (синий).

Левый верхний график является линейным по осям X и Y, а ось Y находится в диапазоне от 0 до 10. Для оси Y нижнего левого графика используется логарифмическая шкала с основанием 10, а по оси Y - от 0,1 до 1000.

На верхнем правом графике используется шкала log-10 только для оси X, а на нижнем правом графике используется шкала log-10 как для оси X, так и для оси Y.

Представление данных в логарифмической шкале может быть полезно, когда данные:

охватывает большой диапазон значений, поскольку использование логарифмов значений, а не фактических значений сокращает широкий диапазон до более управляемого размера;
может содержать экспоненциальные законы или законы власти, поскольку они будут отображаться как прямые линии.

А логарифмическая линейка имеет логарифмическую шкалу, и номограммы часто используют логарифмические шкалы. В среднее геометрическое из двух чисел находится посередине между числами. До появления компьютерной графики логарифмическая миллиметровая бумага был широко используемым научным инструментом.

Лог – логарифмические графики

График в логарифмическом масштабе уравнения линии

Если и вертикальная, и горизонтальная оси графика масштабируются логарифмически, график упоминается как график – журнал.

Полулогарифмические графики

Если бы только ордината или абсцисса масштабируется логарифмически, график называется полулогарифмическим графиком.

Логарифмические единицы

А логарифмическая единица это единица измерения который можно использовать для выражения количества (физический или математический) в логарифмическом масштабе, то есть пропорционально значению логарифм функция, применяемая к соотношению количества и эталонного количества того же типа. Выбор единицы обычно указывает тип количества и основание логарифма.

Примеры

Примеры логарифмических единиц включают единицы емкость хранилища данных (немного, байт ), из Информация и информационная энтропия (нац, Шеннон, запретить ), и из уровень сигнала (децибел, бел, непер ). Логарифмические частотные величины используются в электронике (десятилетие, октава ) и для музыкального тона интервалы (октава, полутон, цент, так далее.). Другие единицы логарифмической шкалы включают Шкала звездных величин Рихтера точка.

Кроме того, некоторые промышленные меры являются логарифмическими, например, стандартные значения для резисторы, то Американский калибр проволоки, то Бирмингемский манометр используется для проволоки и игл и так далее.

Единицы информации

Единицы измерения уровня или разницы уровней

Единицы частотного интервала

Таблица примеров

Единица измерения	Основание логарифма	Базовое количество	Интерпретация
немного	2	количество возможных сообщений	количество информации
байт	$28 = 256$	количество возможных сообщений	количество информации
децибел	$10 (1/10) \approx 1.259$	Любые количество мощности (звуковая мощность, Например)	уровень звуковой мощности (Например)
децибел	$10 (1/20) \approx 1.122$	Любые величина корневой мощности (звуковое давление, Например)	уровень звукового давления (Например)
полутон	$2 (1/12) \approx 1.059$	частота из звук	интервал подачи

Два определения децибела эквивалентны, потому что отношение величины мощности равна квадрату соответствующего отношения корневые степенные величины.^{[нужна цитата ]}

Мотивация

Мотивация, лежащая в основе концепции логарифмических единиц, заключается в том, что определение величины в логарифмической шкале с точки зрения логарифма с определенным основанием равносильно совершению (совершенно произвольного) выбора единицы измерения для этой величины, соответствующей конкретной (и в равной степени произвольно) выбранное основание логарифма. Из-за личности

{ displaystyle log _ {b} a = { frac { log _ {c} a} { log _ {c} b}},}

логарифмы любого заданного числа а на две разные базы (здесь б и c) отличаются только постоянным множителем log_c б. Этот постоянный коэффициент можно рассматривать как коэффициент преобразования для преобразования числового представления чистой (неопределенной) логарифмической величины Log (а) от одной произвольной единицы измерения ([logc] блок) в другой ([журналб] единица), поскольку

{ displaystyle operatorname {Log} (a) = ( log _ {b} a) [ log b] = ( log _ {c} a) [ log c].}

Например, Больцман стандартное определение энтропии S = k перW (где W количество способов организации системы и k является Постоянная Больцмана ) также можно записать более просто как S = Журнал (W), где "Лог" здесь означает неопределенный логарифм, и мы полагаем k = [журнал e]; то есть мы идентифицируем физическую единицу энтропии k с математической единицей [log e]. Эта личность работает, потому что

{ displaystyle ln W = log _ {e} W = { frac { operatorname {Log} (W)} { log e}}.}

Таким образом, мы можем интерпретировать постоянную Больцмана как просто выражение (в терминах более стандартных физических единиц) абстрактной логарифмической единицы [log e], которая необходима для преобразования безразмерной величины чистого числа lnW (который использует произвольный выбор основания, а именно e) до более фундаментальной чистой логарифмической величины Log (W), что не подразумевает никакого особого выбора основания и, следовательно, никакого особого выбора физической единицы измерения энтропии.

Смотрите также

Масштаб

Порядок величины

Приложения

использованная литература

^ «Смысл правила скольжения: культура коренных народов Амазонки демонстрирует универсальное отображение числа в пространстве». ScienceDaily. 2008-05-30. Получено 2008-05-31.

дальнейшее чтение

Дехайн, Станислав; Изар, Вероник; Спелке, Элизабет; Пика, Пьер (2008). «Логарифмический или линейный? Четкие интуитивные представления о числовой шкале в культурах коренных народов Запада и Амазонки». Наука. 320 (5880): 1217–20. Bibcode:2008Научный ... 320.1217D. Дои:10.1126 / science.1156540. ЧВК 2610411. PMID 18511690.
Туффенцаммер, Карл; Шумахер, П. (1953). "Normzahlen - die einstellige Logarithmentafel des Ingenieurs" [Предпочтительные числа - таблица однозначного логарифма инженера]. Werkstattechnik und Maschinenbau (на немецком). 43 (4): 156.
Туффенцаммер, Карл (1956). «Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen» [Децилог, мост между логарифмами, децибелами, непер и предпочтительными числами]. VDI-Zeitschrift (на немецком). 98: 267–274.
Райс, Клеменс (1962). Normung nach Normzahlen [Стандартизация по предпочтительным номерам] (на немецком языке) (1-е изд.). Берлин, Германия: Duncker & Humblot Verlag [де ]. ISBN 978-3-42801242-8. (135 страниц)
Паулин, Евгений (01.09.2007). Logarithmen, Normzahlen, Dezibel, Neper, Phon - natürlich verwandt! [Логарифмы, предпочтительные числа, децибелы, непер, фон - естественно связаны!] (PDF) (на немецком). В архиве (PDF) из оригинала от 18.12.2016. Получено 2016-12-18.

внешние ссылки

"Руководство по GNU Emacs Calc: логарифмические единицы". Gnu.org. Получено 2016-11-23.
Сайт неньютоновского исчисления

[1] «Смысл правила скольжения: культура коренных народов Амазонки демонстрирует универсальное отображение числа в пространстве». ScienceDaily. 2008-05-30. Получено 2008-05-31.

[1]