Энтропия (стрела времени) - Entropy (arrow of time)

Энтропия - одна из немногих величин в физических науках, которая требует определенного направления времени, иногда называемого стрела времени. По мере продвижения "вперед" во времени второй закон термодинамики говорит, что энтропия изолированной системы может увеличиваться, но не уменьшаться. Таким образом, измерение энтропии - это способ отличить прошлое от будущего. В термодинамических системах, которые не закрыты, энтропия может уменьшаться со временем, например живые системы где локальная энтропия снижается за счет увеличения окружающей среды (что приводит к чистому увеличению энтропии), образования типичных кристаллов, работы холодильник и внутри живых организмов.

Так же, как температура Несмотря на то, что это абстрактное понятие, каждый интуитивно чувствует эффекты энтропии. Например, часто очень легко отличить видео, которое воспроизводится вперед или назад. Видео может изобразить дровяной пожар, который тает ближайший ледяной блок, воспроизведенное в обратном порядке, покажет, что лужа воды превратила облако дыма в несгоревшие дрова и при этом замерзла. Удивительно, но в любом случае подавляющее большинство законов физики не нарушается этими процессами, за исключением второй закон термодинамики. Когда закон физики одинаково применяется при обращении времени, говорят, что он показывает Т-симметрия; в этом случае энтропия - это то, что позволяет решить, воспроизводится ли описанное выше видео вперед или назад, поскольку интуитивно мы понимаем, что только при воспроизведении вперед энтропия сцены увеличивается. Из-за второго закона термодинамики энтропия предотвращает макроскопические процессы, демонстрирующие Т-симметрию.

При изучении в микроскопическом масштабе нельзя делать вышеуказанные суждения. Наблюдая за единственной частицей дыма обрушивается на воздух, было бы неясно, воспроизводилось ли видео вперед или назад, и, на самом деле, это было бы невозможно, поскольку применяемые законы показывают Т-симметрию, поскольку оно смещается влево или вправо качественно это не выглядит иначе. Только когда вы изучаете этот газ в макроскопический масштаб что эффекты энтропии становятся заметными. В среднем можно ожидать, что частицы дыма вокруг зажженной спички будут отдаляться друг от друга, распространяясь по доступному пространству. Сгруппировать вместе все частицы было бы астрономически невероятным событием, но вы не можете прокомментировать движение какой-либо одной частицы дыма.

Напротив, некоторые субатомные взаимодействия с участием слабая ядерная сила нарушать сохранение паритета, но очень редко.^{[нужна цитата ]} Согласно CPT теорема, это означает, что они также должны быть время необратимо, и таким образом установить стрела времени. Это, однако, не связано с термодинамической стрелой времени и не имеет ничего общего с повседневным опытом необратимости времени.^[1]

Нерешенная проблема в физике:

Стрела времени: Почему у Вселенной была такая низкая энтропия в прошлом, что привело к различию между прошлый и будущее и второй закон термодинамики ?

(больше нерешенных задач по физике)

Обзор

В Второй закон термодинамики позволяет энтропии оставаться прежним независимо от направления времени. Если энтропия постоянна в любом направлении времени, предпочтительного направления не будет. Однако энтропия может быть постоянной только в том случае, если система находится в максимально возможном состоянии беспорядка, таком как газ, который всегда был и всегда будет равномерно распределен в своем контейнере. Существование термодинамической стрелки времени подразумевает, что система сильно упорядочена только в одном направлении времени, которое по определению было бы «прошлым». Таким образом, этот закон касается граничные условия а не уравнения движения.

Второй закон термодинамики статистический в природе, и поэтому его надежность проистекает из огромного количества частиц, присутствующих в макроскопических системах. В принципе, это не невозможно для всех 6 × 10²³ атомы в крот газа, который самопроизвольно мигрирует в половину емкости; это только фантастически маловероятно - настолько маловероятно, что макроскопического нарушения Второго закона никогда не наблюдалось. Т-симметрия симметрия физических законов относительно преобразования обращения времени. Хотя в ограниченном контексте можно обнаружить эту симметрию, сама наблюдаемая Вселенная не демонстрирует симметрии относительно обращения времени, в первую очередь из-за второго закона термодинамики.

Термодинамическую стрелку часто связывают с космологической стрелой времени, потому что она, в конечном счете, касается граничные условия ранней вселенной. Согласно Большой взрыв теория, Вселенная изначально был очень горячим с равномерно распределенной энергией. Для системы, в которой сила тяжести важно, например, Вселенная, это состояние с низкой энтропией (по сравнению с состоянием с высокой энтропией, когда вся материя коллапсирует в черные дыры, состояние, до которого система может в конечном итоге развиться). По мере роста Вселенной ее температура падает, в результате чего остается меньше энергии [на единицу объема пространства] для выполнения работы в будущем, чем было доступно в прошлом. Кроме того, возмущения в плотности энергии растут (со временем образуя галактики и звезды ). Таким образом, сама Вселенная имеет четко выраженную термодинамическую стрелу времени. Но это не касается вопроса о том, почему первоначальное состояние Вселенной было низким энтропийным состоянием. Если бы космическое расширение остановилось и обратилось вспять из-за гравитации, температура Вселенной снова стала бы выше, но ее энтропия также продолжала бы расти из-за продолжающегося роста возмущений и возможного черная дыра формирование^[2] до последних стадий Большой хруст когда энтропия была бы ниже, чем сейчас.^{[нужна цитата ]}

Пример очевидной необратимости

Рассмотрим ситуацию, когда большой контейнер заполнен двумя отдельными жидкостями, например, красителем с одной стороны и водой с другой. Без барьера между двумя жидкостями случайное столкновение от их молекулы приведет к тому, что со временем они станут более смешанными. Однако, если краситель и воду смешать, не следует ожидать, что они снова разделятся, если их предоставить самим себе. Фильм о микшировании будет казаться реалистичным при воспроизведении вперед, но нереалистичным при воспроизведении назад.

Если большой контейнер замечен на ранней стадии процесса смешивания, он может оказаться частично перемешанным. Было бы разумно заключить, что без внешнего вмешательства жидкость достигла этого состояния, потому что она была более упорядоченной в прошлом, когда было большее разделение, и будет более беспорядочным или смешанным в будущем.

Теперь представьте, что эксперимент повторяется, но на этот раз всего с несколькими молекулами, возможно, с десятью в очень маленьком контейнере. Можно легко представить себе, что, наблюдая за случайным столкновением молекул, может произойти - только случайно - что молекулы будут аккуратно разделены: все молекулы красителя с одной стороны, а все молекулы воды - с другой. О том, что это может происходить время от времени, можно сделать вывод из теорема о флуктуациях; таким образом, молекулы не могут отделиться друг от друга. Однако для большого числа молекул настолько маловероятно, что придется ждать, в среднем, во много раз дольше, чем возраст Вселенной, чтобы это произошло. Таким образом, фильм, в котором показано большое количество молекул, разделяющих себя, как описано выше, будет казаться нереальным, и можно будет сказать, что фильм воспроизводился в обратном порядке. См Больцмана Второй закон как закон беспорядка.

Математика стрелки

В математика за стрела времени, энтропия, и основа второй закон термодинамики происходят из следующей схемы, подробно описанной Карно (1824 г.), Клапейроном (1832 г.) и Клаузиусом (1854 г.):

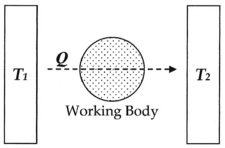
Здесь, как показывает общий опыт, когда горячей тело Т₁, например, печь, находится в физическом контакте, например, через массу жидкости (рабочий орган ), с холодным телом Т₂, например, струя холодной воды, энергия неизменно перетекает от горячего к холодному в виде высокая температура Q, и учитывая время система достигнет равновесие. Энтропия, определяемая как Q / T, была задумана Рудольф Клаузиус как функция для измерения молекулярного необратимость этого процесса, то есть диссипативной работы, которую атомы и молекулы совершают друг над другом во время преобразования.

На этой диаграмме можно вычислить изменение энтропии ΔS для прохождения количества тепла Q от температура Т₁, через «рабочее тело» жидкости (см. Тепловой двигатель ), который обычно представлял собой массу пара, до температуры Т₂. Более того, ради аргументации можно было предположить, что в рабочем теле всего две молекулы воды.

Затем, если мы сделаем присвоение, как первоначально сделал Клаузиус:

{displaystyle S = {frac {Q} {T}}}

Тогда изменение энтропии или «значение эквивалентности» для этого преобразования:

{displaystyle Delta S = S_ {mathit {final}} - S_ {mathit {initial}},}

что равно:

{displaystyle Delta S = left ({frac {Q} {T_ {2}}} - {frac {Q} {T_ {1}}} ight)}

и, вынося Q на множители, мы получаем следующую форму, выведенную Клаузиусом:

{displaystyle Delta S = Qleft ({frac {1} {T_ {2}}} - {frac {1} {T_ {1}}} ight)}

Так, например, если Q было 50 единиц, Т₁ изначально было 100 градусов, а Т₂ было первоначально 1 градус, то изменение энтропии для этого процесса будет 49,5. Следовательно, энтропия увеличилась для этого процесса, процесс занял определенное количество «времени», и можно связать увеличение энтропии с течением времени. Следовательно, для такой конфигурации системы это «абсолютное правило». Это правило основано на том, что все природные процессы необратимый в силу того факта, что молекулы системы, например две молекулы в резервуаре, не только выполняют внешнюю работу (например, толкают поршень), но также выполняют внутреннюю работу друг с другом пропорционально теплу, используемому для выполнения работа (см .: Механический эквивалент тепла ) во время процесса. Энтропия объясняет тот факт, что существует внутреннее межмолекулярное трение.

Корреляции

Важное различие между прошлым и будущим заключается в том, что в любой системе (например, в газе из частиц) ее начальные условия обычно таковы, что ее различные части не коррелируют, но по мере развития системы и ее различных частей, взаимодействующих друг с другом, они становятся коррелированными.^[3] Например, всякий раз, когда мы имеем дело с газом частиц, всегда предполагается, что его начальные условия таковы, что нет корреляции между состояниями различных частиц (т.е. скорости и положения разных частиц полностью случайны, вплоть до необходимости соответствовать макросостояние системы). Это тесно связано со вторым законом термодинамики: например, в конечной системе, взаимодействующей с конечными резервуарами тепла, энтропия эквивалентна корреляциям система-резервуар, и, таким образом, оба увеличиваются вместе.^[4]

Возьмем, например, (эксперимент A) закрытый ящик, который вначале наполовину заполнен идеальным газом. По прошествии времени газ, очевидно, расширяется, чтобы заполнить всю коробку, так что конечное состояние - это коробка, полная газа. Это необратимый процесс, поскольку, если ящик полон вначале (эксперимент B), он не станет заполнен только наполовину позже, за исключением очень маловероятной ситуации, когда частицы газа имеют совершенно особые положения и скорости. Но это именно потому, что мы всегда предполагаем, что начальные условия таковы, что частицы имеют случайные местоположения и скорости. Это неверно для конечных условий системы, потому что частицы взаимодействовали между собой, так что их местоположения и скорости стали зависимыми друг от друга, то есть коррелированными. Это можно понять, если мы посмотрим на эксперимент A назад во времени, который мы назовем экспериментом C: теперь мы начинаем с контейнера, полного газа, но частицы не имеют случайных местоположений и скоростей; скорее, их местоположение и скорость настолько специфичны, что через некоторое время все они перемещаются в одну половину коробки, которая является конечным состоянием системы (это начальное состояние эксперимента A, потому что теперь мы смотрим на тот же эксперимент наоборот!). Взаимодействия между частицами теперь не создают корреляции между частицами, а фактически превращают их (по крайней мере, кажущиеся) случайными, «отменяя» ранее существовавшие корреляции. Единственная разница между экспериментом C (который противоречит Второму закону термодинамики) и экспериментом B (который подчиняется Второму закону термодинамики) заключается в том, что в первом случае частицы не коррелированы в конце, а во втором частицы не коррелированы в начало.^{[нужна цитата ]}

Фактически, если все микроскопические физические процессы обратимы (см. Обсуждение ниже), то второй закон термодинамики может быть доказан для любой изолированной системы частиц с начальными условиями, в которых состояния частиц не коррелированы. Для этого необходимо признать разницу между измеренной энтропией системы, которая зависит только от ее макросостояние (его объем, температура и т. д.) - и его информационная энтропия,^[5] количество информации (количество битов компьютера), необходимое для описания точного микросостояние системы. Измеренная энтропия не зависит от корреляций между частицами в системе, поскольку они влияют не на ее макросостояние, а на информационную энтропию. делает зависят от них, потому что корреляции снижают случайность системы и, таким образом, уменьшают количество информации, необходимой для ее описания.^[6] Следовательно, в отсутствие таких корреляций две энтропии идентичны, но в остальном информационная энтропия меньше измеренной энтропии, и разницу можно использовать как меру количества корреляций.

Теперь по Теорема Лиувилля, обращение времени всех микроскопических процессов подразумевает, что объем информации, необходимый для описания точного микросостояние изолированной системы (ее теоретико-информационного совместная энтропия ) постоянна во времени. Эта совместная энтропия равна предельной энтропии (энтропия, предполагающая отсутствие корреляций) плюс энтропия корреляции (взаимная энтропия или ее отрицательная величина. взаимная информация ). Если мы изначально предполагаем отсутствие корреляций между частицами, то эта совместная энтропия - это просто предельная энтропия, которая представляет собой просто начальную термодинамическую энтропию системы, деленную на Постоянная Больцмана. Однако если это действительно начальные условия (а это принципиальное предположение), то такие корреляции формируются со временем. Другими словами, происходит уменьшение взаимной энтропии (или увеличение взаимной информации), и в течение некоторого времени корреляции (взаимная информация) между частицами только увеличиваются со временем. Следовательно, термодинамическая энтропия, пропорциональная предельной энтропии, также должна увеличиваться со временем. ^[7] (обратите внимание, что «не слишком долго» в этом контексте относится ко времени, необходимому в классической версии системы, чтобы она прошла через все свои возможные микросостояния - время, которое можно приблизительно оценить как ${displaystyle au e ^ {S}}$ , куда ${displaystyle au}$ - время между столкновениями частиц, а S - энтропия системы. В любом практическом случае это время огромно по сравнению со всем остальным). Обратите внимание, что корреляция между частицами не является полностью объективной величиной. Невозможно измерить взаимную энтропию, можно только измерить ее изменение, если предположить, что можно измерить микросостояние. Термодинамика ограничивается случаем, когда микросостояния не могут быть различимы, а это означает, что можно измерить только предельную энтропию, пропорциональную термодинамической энтропии, и в практическом смысле она всегда увеличивается.

Стрела времени в различных явлениях

Явления, которые происходят по-разному в зависимости от их направления времени, в конечном итоге могут быть связаны с Второй закон термодинамики^{[нужна цитата ]}Например, кубики льда тают в горячем кофе, а не собираются из него, а блок, скользящий по шероховатой поверхности, скорее замедляется, чем ускоряется. Идея о том, что мы можем помнить прошлое, а не будущее, называется «психологической стрелой времени» и имеет глубокую связь с Демон Максвелла и физика информации; память связана со вторым законом термодинамики, если рассматривать ее как корреляцию между клетками мозга (или компьютерными битами) и внешним миром: поскольку такие корреляции увеличиваются со временем, память связана с прошлыми событиями, а не с будущими событиями.^{[нужна цитата ]}.

Текущее исследование

Текущие исследования сосредоточены главным образом на математическом описании термодинамической стрелы времени в классических или квантовых системах, а также на понимании ее происхождения с точки зрения космологический граничные условия.

Динамические системы

Некоторые текущие исследования в динамические системы указывает возможное «объяснение» стрелы времени.^{[нужна цитата ]} Есть несколько способов описать эволюцию динамической системы во времени. В классической схеме рассматривается дифференциальное уравнение, где одним из параметров явно является время. По самой природе дифференциальных уравнений решения таких систем обратимы во времени. Однако многие из интересных случаев либо эргодический или же смешивание, и есть серьезные подозрения, что перемешивание и эргодичность каким-то образом лежат в основе фундаментального механизма стрелы времени.

Смешивающие и эргодические системы не имеют точных решений, и поэтому доказательство необратимости времени в математическом смысле (по состоянию на 2006 г.^{[Обновить]}) невозможно. Некоторого прогресса можно добиться, изучая модели с дискретным временем или разностные уравнения. Многие модели с дискретным временем, такие как повторяющиеся функции рассматриваемые в популярных программах для рисования фракталов, явно не обратимы во времени, поскольку с любой заданной точкой «в настоящем» может быть связано несколько различных «прошлых»: действительно, набор всех прошлых известен как Юля набор. Поскольку такие системы имеют встроенную необратимость, их неуместно использовать для объяснения того, почему время необратимо.

Есть и другие системы, которые хаотичны и также явно обратимы во времени: среди них карта пекаря, которая также точно решается. Интересным направлением исследования является изучение решений таких систем не путем повторения динамической системы во времени, а вместо этого для изучения соответствующих Оператор Фробениуса-Перрона или же оператор передачи для системы. Для некоторых из этих систем можно явно математически показать, что операторы переноса не являются класс трассировки. Это означает, что у этих операторов нет уникального собственное значение спектр, не зависящий от выбора базиса. В случае карты пекаря можно показать, что существует несколько уникальных и неэквивалентных диагонализаций или баз, каждая с различным набором собственных значений. Именно это явление можно предложить как «объяснение» стрелы времени. То есть, хотя итеративная система с дискретным временем явно симметрична по времени, оператор переноса - нет. Кроме того, оператор переноса может быть диагонализован одним из двух неэквивалентных способов: один описывает эволюцию системы в прямом времени, а второй описывает эволюцию в обратном времени.

По состоянию на 2006 год этот тип времени-нарушение симметрии был продемонстрирован только для очень небольшого числа точно решаемых систем с дискретным временем. Оператор переноса для более сложных систем не был сформулирован последовательно, и его точное определение связано с множеством тонких трудностей. В частности, не было показано, что он имеет нарушенную симметрию для простейших точно решаемых эргодических систем с непрерывным временем, таких как Бильярд Адамара, или Аносов поток на касательном пространстве PSL (2, R).

Квантовая механика

Исследования необратимости в квантовой механике имеют несколько различных направлений. Один из путей - изучение оснащенные гильбертовы пространства, и, в частности, как смешиваются дискретные и непрерывные спектры собственных значений^{[нужна цитата ]}. Например, рациональное число полностью переплетаются с действительные числа и при этом обладают уникальным, отличным набором свойств. Есть надежда, что изучение гильбертовых пространств с подобным перемешиванием позволит лучше понять стрелу времени.

Другой отличный подход заключается в изучении квантовый хаос с помощью которых делаются попытки квантовать системы как классически хаотические, эргодические или смешанные.^{[нужна цитата ]} Полученные результаты не отличаются от результатов, полученных с помощью метода оператора переноса. Например, квантование Газ Больцмана, то есть газ твердых (упругих) точечных частиц в прямоугольном ящике показывает, что собственные функции представляют собой фракталы, заполняющие пространство, которые занимают весь ящик, и что собственные значения энергии расположены очень близко друг к другу и имеют «почти непрерывный» спектр ( для конечного числа частиц в ящике спектр обязательно должен быть дискретным). Если начальные условия таковы, что все частицы ограничены одной стороной коробки, система очень быстро эволюционирует в систему, в которой частицы заполняют всю коробку. Даже когда все частицы изначально находятся на одной стороне ящика, их волновые функции на самом деле пронизывают весь ящик: они конструктивно интерферируют с одной стороны и деструктивно мешают с другой. Затем аргументируется необратимость, отмечая, что «почти невозможно» «случайно» расположить волновые функции в каком-либо маловероятном состоянии: такие устройства представляют собой набор нулевых значений. мера. Поскольку собственные функции являются фракталами, большая часть языка и механизмов энтропии и статистической механики может быть импортирована для обсуждения и аргументации квантового случая.^{[нужна цитата ]}

Космология

Некоторые процессы, в которых участвуют частицы высоких энергий и регулируются слабая сила (Такие как К-мезон распад) нарушают симметрию между направлениями времени. Однако все известные физические процессы делать сохранить более сложную симметрию (Симметрия CPT ), и поэтому не имеют отношения к второй закон термодинамики, или к повседневному опыту стрелы времени. Заметным исключением является коллапс волновой функции в квантовая механика, необратимый процесс, который считается либо реальным ( Копенгагенская интерпретация ) или только видимый (по Интерпретация многих миров квантовой механики). В любом случае коллапс волновой функции всегда следует квантовая декогеренция, процесс, который считается результатом второго закона термодинамики.

В вселенная находился в однородном состоянии с высокой плотностью на самых ранних стадиях, вскоре после Большой взрыв. Горячий газ в ранней Вселенной был близок к термодинамическому равновесию (см. Проблема горизонта ); в системах, где гравитация играет важную роль, это состояние низкой энтропии из-за отрицательная теплоемкость таких систем (это в отличие от негравитационных систем, где термодинамическое равновесие состояние максимальной энтропии). Более того, из-за его небольшого объема по сравнению с будущими эпохами энтропия была еще ниже, поскольку расширение газа увеличивает его энтропию. Таким образом, раннюю Вселенную можно считать высокоупорядоченной. Обратите внимание, что однородность этого раннего состояния, близкого к равновесию, объясняется теорией космическая инфляция.

Согласно этой теории Вселенная (или, скорее, ее доступная часть, радиус 46 миллиардов световых лет вокруг Земли) возникла из крошечного, полностью однородного объема (части гораздо большей Вселенной), который сильно расширился; следовательно, это было очень заказано. Затем квантовые процессы, связанные с его расширением, создавали флуктуации таким образом, чтобы эти флуктуации проходили через квантовая декогеренция, так что они стали некоррелированными для любого практического использования. Предполагается, что это даст желаемые начальные условия, необходимые для Второго закона термодинамики; различные декогерентные состояния в конечном итоге эволюционировали в различные специфические структуры галактик и звезд.

Вселенная, по-видимому, открытая вселенная, так что его расширение никогда не прекратится, но это интересный мысленный эксперимент представить, что произошло бы, если бы Вселенная была закрыто. В таком случае его расширение остановится в определенное время в отдаленном будущем, а затем начнет сокращаться. Более того, замкнутая вселенная конечна, и непонятно, что будет с ней. Второй закон термодинамики в таком случае. Можно представить по крайней мере два разных сценария, хотя на самом деле правдоподобен только первый, поскольку другой требует очень плавной космической эволюции, вопреки тому, что наблюдается:

Сегодня в научном сообществе широко распространено мнение о том, что гладкие начальные условия приводят к крайне негладкому конечному состоянию, и что это фактически источник термодинамической стрелы времени.^[8] Гравитационный системы стремятся гравитационный коллапс для уплотнения тел, таких как черные дыры (явление, не связанное с коллапсом волновой функции), так что когда Вселенная заканчивается Большой хруст это очень отличается от Большой взрыв работать в обратном направлении, так как распределение материи будет очень негладким; когда Вселенная сжимается, такие компактные тела сливаются во все большие и большие черные дыры. Возможно даже, что у Вселенной не может быть одновременно плавного начала и плавного конца. Заметим, что в этом сценарии плотность энергии Вселенной на заключительных стадиях ее сжатия намного больше, чем на соответствующих начальных стадиях ее расширения (отсутствует деструктивное вмешательство в отличие от первого сценария, описанного выше), и состоит в основном из черных дыр, а не из свободных частиц.
В высшей степени противоречивое мнение состоит в том, что вместо этого стрелка времени повернет вспять.^[9] Квантовые флуктуации, которые за это время превратились в галактики и звезды, будут в суперпозиция таким образом, что весь описанный выше процесс обращен вспять, то есть флуктуации стираются деструктивное вмешательство и снова достигается полная однородность. Таким образом, вселенная заканчивается Большой хруст, что похоже на его начало в Большой взрыв. Поскольку они полностью симметричны, а конечное состояние очень упорядочено, энтропия должна уменьшаться ближе к концу Вселенной, так что Второй закон термодинамики меняется на противоположный, когда Вселенная сжимается. Это можно понять следующим образом: в очень ранней Вселенной взаимодействия между флуктуациями создавали запутанность (квантовые корреляции ) между частицами, разбросанными по Вселенной; во время расширения эти частицы стали настолько далекими, что эти корреляции стали незначительными (см. квантовая декогеренция ). Когда расширение останавливается и Вселенная начинает сжиматься, такие коррелированные частицы снова приходят на контакт (после того, как кружат вокруг Вселенной), и энтропия начинает уменьшаться, потому что сильно коррелированные начальные условия могут привести к уменьшению энтропии. Другими словами, по мере приближения далеких частиц обнаруживается все больший и больший порядок, потому что эти частицы сильно коррелируют с частицами, прибывшими раньше. В этом сценарии космологический стрела времени является причиной как термодинамической стрелы времени, так и квантовой стрелы времени. Оба будут медленно исчезать, когда вселенная остановится, а позже будут перевернуты.

В первом и более согласованном сценарии именно разница между начальным и конечным состояниями Вселенной отвечает за термодинамическую стрелу времени. Это не зависит от космологической стрелы времени.

Смотрите также

дальнейшее чтение

Halliwell, J.J .; и другие. (1994). Физические истоки асимметрии времени. Кембридж. ISBN 0-521-56837-4. (технический).
Макки, Майкл С. (1992). Стрела времени: истоки термодинамического поведения. Берлин Гейдельберг Нью-Йорк: Спрингер. ISBN 3-540-94093-6. OCLC 28585247. ... показано, что для глобальной эволюции энтропии до максимального значения ... необходимо и достаточно что система обладает свойством, известным как точность. ... эти критерии предполагают, что все сформулированные в настоящее время физические законы могут не лежать в основе термодинамического поведения, которое мы наблюдаем каждый день нашей жизни. (стр. xi)
Довер перепечатал монографию в 2003 г. (ISBN 0486432432). Краткий документ, в котором перечислены «основные моменты этого аргумента, исправлены запутанные моменты изложения ... и сделаны выводы более убедительно, чем раньше» см. Макки, Майкл С. (2001). «Микроскопическая динамика и второй закон термодинамики» (PDF). В Мугнаи, C .; Ranfagni, A .; Шульман, Л. (ред.). Стрела времени, квантовые измерения и сверхсветовое поведение. Рим: Consiglio Nazionale Delle Ricerche. С. 49–65. ISBN 88-8080-024-8. Архивировано из оригинал (PDF) на 2011-07-25.
Шон М. Кэрролл, Из вечности сюда: поиски окончательной теории времени

внешняя ссылка

Термодинамическая асимметрия во времени в Интернете Стэнфордская энциклопедия философии

[1] Цена, Хью (2004). «Термодинамическая стрела: загадки и псевдопазлы». arXiv:физика / 0402040.

[2] Пенроуз, Р. Дорога к реальности стр. 686-734

[3] Физические истоки асимметрии времени, п. 109.

[4] Эспозито М., Линденберг К. и Ван ден Брок К. (2010). Производство энтропии как взаимосвязь между системой и резервуаром. Новый журнал физики, 12 (1), 013013.

[5] Физические истоки асимметрии времени, п. 35.

[6] Физические истоки асимметрии времениС. 35-38.

[7] «Некоторые заблуждения об энтропии». Архивировано из оригинал на 2012-02-04. Получено 2011-02-13.

[8] Лебовиц, Джоэл (2008). «Стрела времени и энтропия Больцмана». Scholarpedia. 3 (4): 3448. Bibcode:2008SchpJ ... 3.3448L. Дои:10.4249 / scholarpedia.3448.

[9] Хокинг, С. В. (1985). «Стрела времени в космологии». Физический обзор D. 32 (10): 2489–2495. Bibcode:1985ПхРвД..32.2489Н. Дои:10.1103 / PhysRevD.32.2489. PMID 9956019.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]