Уравнение Сакура – ​​Тетрода - Sackur–Tetrode equation

В Уравнение Сакура – ​​Тетрода это выражение для энтропия из одноатомный идеальный газ.^[1]

Он назван в честь Хьюго Мартин Тетроде^[2] (1895–1931) и Отто Сакур^[3] (1880–1914), который разработал его независимо как решение газовой статистики Больцмана и уравнений энтропии примерно в то же время, в 1912 году.^[4]

Формула

Уравнение Сакура – ​​Тетроде выражает энтропию ${ displaystyle S}$ одноатомного идеального газа с точки зрения его термодинамического состояния, в частности, его объема ${ displaystyle V}$, внутренняя энергия ${ displaystyle U}$, а количество частиц ${ displaystyle N}$:^[1][4]

${ displaystyle { frac {S} {k_ {B} N}} = ln left [{ frac {V} {N}} left ({ frac {4 pi m} {3h ^ {2 }}} { frac {U} {N}} right) ^ {3/2} right] + { frac {5} {2}}}$

куда

${ Displaystyle к _ { mathrm {B}}}$ =	Постоянная Больцмана
${ displaystyle m}$ =	Масса частицы газа
${ displaystyle h}$ =	Постоянная Планка

Уравнение также можно выразить через длина тепловой волны ${ displaystyle Lambda}$:

${ displaystyle { frac {S} {k_ {B} N}} = ln left ({ frac {V} {N Lambda ^ {3}}} right) + { frac {5} { 2}}}$

Кривые зависимости энтропии от температуры для классических и квантовых идеальных газов (Ферми газ, Бозе-газ ) в трех измерениях. Хотя все они хорошо согласуются при высоких температурах, они расходятся при низких температурах, когда классическая энтропия (уравнение Сакура – ​​Тетроде) начинает приближаться к отрицательным значениям.

Для вывода уравнения Сакура – ​​Тетрода см. Парадокс гиббса. Об ограничениях, налагаемых на энтропию идеального газа только термодинамикой, см. идеальный газ статья.

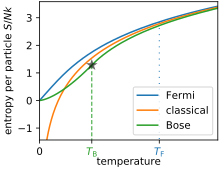
В приведенных выше выражениях предполагается, что газ находится в классическом режиме и описывается уравнением Статистика Максвелла – Больцмана (с «правильным счетом Больцмана»). Из определения длина тепловой волны, это означает, что уравнение Сакура – ​​Тетрода справедливо только тогда, когда

${ displaystyle { frac {V} {N Lambda ^ {3}}} gg 1}$

Фактически энтропия, предсказываемая уравнением Сакура – ​​Тетрода, приближается к отрицательной бесконечности, когда температура приближается к нулю.

Константа Сакура – ​​Тетроде

В Константа Сакура – ​​Тетроде, написано S₀/р, равно S/k_BN оценивается при температуре Т = 1 кельвин, в стандартное давление (100 кПа или 101,325 кПа, необходимо указать) для одного крот идеального газа, состоящего из частиц с массой, равной постоянная атомной массы (м_ты = 1.66053906660(50)×10⁻²⁷ кг^[5]). Его 2018 CODATA рекомендуемое значение:

S₀/р = −1.15170753706(45) за п^о = 100 кПа^[6]

S₀/р = −1.16487052358(45) за п^о = 101,325 кПа.^[7]

Теоретико-информационная интерпретация

В добавок к термодинамическая перспектива энтропии, инструменты теория информации может использоваться для предоставления информационная перспектива энтропии. В частности, можно вывести уравнение Сакура – ​​Тетрода в терминах теории информации. Общая энтропия представлена ​​как сумма четырех индивидуальных энтропий, то есть четырех различных источников недостающей информации. Это позиционная неопределенность, неопределенность импульсов, квантово-механическая принцип неопределенности, а неразличимость частиц.^[8] Суммируя четыре части, уравнение Сакура – ​​Тетрода получается как

${ displaystyle { begin {align} { frac {S} {k_ {B} N}} & = [ ln V] + left [{ frac {3} {2}} ln left (2 pi mk_ {B} T right) right] + [- 3 ln h] + left [- { frac { ln N!} {N}} right] & приблизительно ln left [{ frac {V} {N}} left ({ frac {2 pi mk_ {B} T} {h ^ {2}}} right) ^ { frac {3} {2}} right] + { frac {5} {2}} end {align}}}$

В выводе используется Приближение Стирлинга, ${ Displaystyle ln N! приблизительно N ln N-N}$. Строго говоря, использование аргументов с размерами логарифмов неверно, однако их использование является «ярлыком», сделанным для простоты. Если каждый логарифмический аргумент был разделен на неопределенное стандартное значение, выраженное в терминах неопределенной стандартной массы, длины и времени, эти стандартные значения аннулировались бы в окончательном результате, давая тот же вывод. Отдельные члены энтропии не будут абсолютными, а скорее будут зависеть от выбранных стандартов и будут отличаться для разных стандартов на аддитивную константу.

Рекомендации

дальнейшее чтение

• Emch, G. G .; Лю, К. (2002), Логика термостатистической физики, Springer-Verlag, Глава 3: Кинетическая теория газов.
• Куцойаннис, Д. (2013), "Физика неопределенности, парадокс Гиббса и неразличимые частицы", Исследования по истории и философии науки Часть B, 44 (4): 480–489, Bibcode:2013ШПМП..44..480К, Дои:10.1016 / j.shpsb.2013.08.007. (Это выводит уравнение Сакура – ​​Тетрода другим способом, также основанным на информации.)
• Paños, F.J .; Перес, Э. (2015), "Уравнение Сакура – ​​Тетроде в лаборатории", Европейский журнал физики, 36 (5): 055033, Bibcode:2015EJPh ... 36e5033J, Дои:10.1088/0143-0807/36/5/055033.
• Уильямс, Ричард (2009), «Уравнение Сакура – ​​Тетрода: как энтропия встречается с квантовой механикой», Новости APS, 18 (8).