Пермутоэдр - Permutohedron

Перммутоэдр 4-го порядка

В математика, то пермутоэдр порядка п является (п - 1) -мерный многогранник встроен в п-мерное пространство. Его вершина координаты перестановки из первых п натуральные числа. Ребра - это кратчайшие возможные соединения между этими точками. Две перестановки, соединенные ребром, различаются в двух местах, а числа на этих местах являются соседями.

На изображении справа показан пермутоэдр 4-го порядка, который является усеченный октаэдр. Его вершины - это 24 перестановки из (1, 2, 3, 4). Параллельные кромки имеют одинаковый цвет кромки. 6 цветов краев соответствуют 6 возможным транспозиции из 4 элементов, т.е. они указывают, в каких двух местах различаются связанные перестановки. (Например, красные края соединяют перестановки, которые различаются в последних двух местах.)

История

В соответствии с Гюнтер М. Циглер (1995 ), пермутоэдры впервые были изучены Питер Хендрик Шуте (1911 ). Название пермутоэдр был придуман Жоржем Т. Гильбо и Пьер Розенштиль (1963 ). Они описывают это слово как варварское, но легко запоминающееся и подвергают критике своих читателей.^[1]

Альтернативное написание пермутаэдр иногда также используется.^[2] Перммутоэдры иногда называют многогранники перестановок, но эта терминология также используется для связанных Многогранник Биркгофа, определяемую как выпуклая оболочка матрицы перестановок. В более общем плане В. Джозеф Боуман (1972 ) использует этот термин для любого многогранника, вершины которого имеют биекция с перестановками некоторого множества.

Вершины, ребра и фасеты

вершины, края, грани, лица
Размер лица

d = п - k

.

   к = 1 2 3 4 5п1      1                               12      1    2                          33      1    6    6                    134      1   14   36   24               755      1   30  150  240  120         541

Перммутоэдр порядка $п$ имеет $п!$ вершины, каждая из которых смежна с $п - 1$ другие.Количество ребер равно $(п - 1) п! / 2$ , а их длина $\sqrt 2$ .

Две соединенные вершины отличаются заменой двух координат, значения которых отличаются на 1.^[3] Пара переставленных мест соответствует направлению кромки. (В пример изображения вершины $(3, 2, 1, 4)$ и $(2, 3, 1, 4)$ соединены синей кромкой и отличаются заменой местами 2 и 3 на первых двух местах. Значения 2 и 3 отличаются на 1. Все синие края соответствуют перестановкам координат в первых двух местах.)

Количество грани является $2 п - 2$ , поскольку они соответствуют непустым собственно подмножества $S$ из ${1 \dots п}$ .Вершины фасета, соответствующие подмножеству $S$ общее, что их координаты на местах в $S$ меньше чем прочее. ^[4]

Примеры фасетов
Для порядка 3 гранями являются 6 ребер, а для порядка 4 - 14. лица. Координаты на местах $я$ куда $я \in S$ отмечены темным фоном. Видно, что они меньше остальных. Квадрат вверху соответствует подмножеству ${3, 4}$ . В четырех его вершинах координаты двух последних мест имеют наименьшие значения (а именно 1 и 2).
заказ 3		заказ 4
1-элементные подмножества	2-элементные подмножества	1-элементные подмножества	2-элементные подмножества	3-элементные подмножества

В более общем плане лица размерностей от 0 (вершин) до $п - 1$ (сам пермутоэдр) соответствуют строгие слабые порядки из набора ${1 \dots п}$ . Итак, количество всех лиц - это $п$ -го заказанный номер звонка.^[5]Лицо измерения $d$ соответствует заказу с $k = п - d$ классы эквивалентности.

Примеры лиц

заказ 3

заказ 4

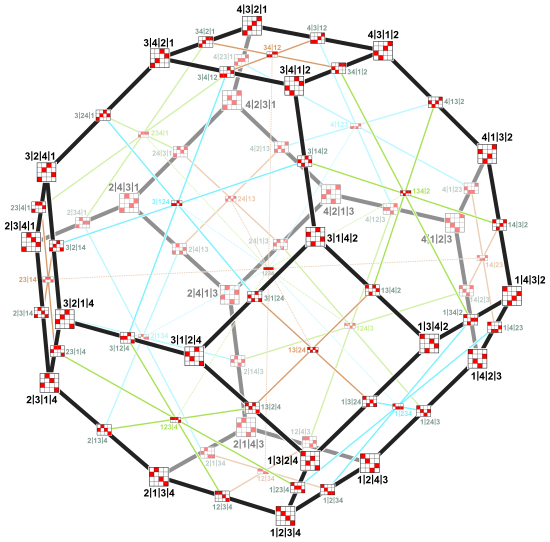На изображениях выше показаны решетки для лица пермутоэдров 3 и 4 порядков (без пустых лиц).
Каждый центр грани помечен строгим слабым порядком. квадрат сверху как 3 4 | 1 2, который представляет $({3, 4}, {1, 2})$ .
Заказы частично заказанный к уточнение, причем более тонкие находятся снаружи.
Двигаясь по край «внутрь» означает слияние двух соседних классов эквивалентности.

Метки вершин а | б | c | d интерпретируется как перестановки (а, б, в, г) те, которые образуют граф Кэли.

Грани среди лиц
Вышеупомянутые фасеты находятся среди этих граней и соответствуют порядкам с двумя классами эквивалентности. Первый используется как подмножество $S$ присваивается фасету, поэтому порядок $(S, S c)$ . На изображениях ниже показано, как грани $п$ -пермутоэдру соответствуют упрощенный проекция $п$ -куб. Бинарные координатные метки соответствуют подмножествам $S$ , например 0011 в ${3, 4}$ . (Вершина, спроецированная в центр, не соответствует фасете. $п$ -куб, не являющийся частью проекции.)

Количество граней измерения $d = п - k$ в пермутоэдре порядка $п$ задается треугольником $Т$ (последовательность A019538 в OEIS ):
${displaystyle T (n, k) = k! cdot left {{n atop k} ight}}$ с ${displaystyle extstyle left {{n поверх k} ight}}$ представляющий Числа Стирлинга второго рода
Он показан справа вместе с суммами строк, заказанные номера Bell.

Другие свойства

Пермутоэдрический граф Кэли группы S₄ (видеть здесь для сравнения с пермутоэдром)

Пермутоэдр вершинно-транзитивный: the симметричная группа S_п действует на пермутоэдре перестановкой координат.

Перммутоэдр - это зонотоп; переведенная копия пермутоэдра может быть сгенерирована как Сумма Минковского из п(п − 1)/2 отрезки линии, соединяющие пары стандартная основа векторов.^[6]

Вершины и ребра пермутоэдра равны изоморфный к одному из Графики Кэли из симметричная группа, а именно тот генерируется посредством транспозиции которые меняют местами последовательные элементы. Вершинами графа Кэли являются обратный перестановки тех, что в пермутоэдре.^[7] На изображении справа показан граф Кэли S4. Цвета его краев представляют 3 генерирующих транспозиции: (1, 2), (2, 3), (3, 4)

Этот граф Кэли Гамильтониан; гамильтонов цикл может быть найден Алгоритм Штейнхауса – Джонсона – Троттера.

Тесселяция пространства

Месселяция пространства пермутоэдрами 3 и 4 порядков

Перммутоэдр порядка п полностью лежит в (п - 1) -мерная гиперплоскость, состоящая из всех точек, сумма координат которых равна числу

1 + 2 + … + п = п(п + 1)/2.

Более того, эту гиперплоскость можно выложенный плиткой бесконечно многими переведено копии пермутоэдра. Каждый из них отличается от основного пермутоэдра элементом определенного (п - 1) -мерный решетка, который состоит из п-наборы целых чисел, сумма которых равна нулю и которые остатки (по модулю п) все равны:

Икс₁ + Икс₂ + … + Икс_п = 0, Икс₁ ≡ Икс₂ ≡ … ≡ Икс_п (мод п).

Это решетка ${displaystyle A_ {n-1} ^ {*}}$ , то двойная решетка из корневая решетка ${displaystyle A_ {n-1}}$ . Другими словами, пермутоэдр - это Ячейка Вороного за ${displaystyle A_ {n-1} ^ {*}}$ . Соответственно, эту решетку иногда называют пермутоэдрической решеткой.^[8]

Таким образом, пермутоэдр 4-го порядка, показанный выше, разбивает трехмерное пространство на мозаику путем сдвига. Здесь трехмерное пространство - это аффинное подпространство 4-мерного пространства р⁴ с координатами Икс, у, z, ш который состоит из 4-х наборов действительных чисел, сумма которых равна 10,

Икс + у + z + ш = 10.

Легко проверить, что для каждого из следующих четырех векторов

(1,1,1, −3), (1,1, −3,1), (1, −3,1,1) и (−3,1,1,1),

сумма координат равна нулю, и все координаты равны 1 (mod 4). Любые три из этих векторов генерировать решетка трансляций.

Тесселяции, сформированные таким образом из пермутоэдров порядка 2, порядка 3 и порядка 4, соответственно, являются апейрогон, регулярный шестиугольная черепица, а усеченные кубические соты. Двойные мозаики содержат все симплекс фасеты, хотя они не являются правильными многогранниками выше порядка-3.

Примеры

Заказ 2	Заказ 3	Заказ 4	Заказ 5	Заказ 6
2 вершины	6 вершин	24 вершины	120 вершин	720 вершин

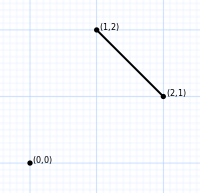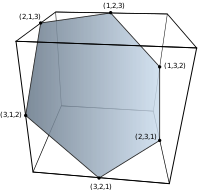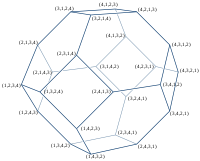отрезок	шестиугольник	усеченный октаэдр	омниусеченный 5-элементный	омниусеченный 5-симплексный

Смотрите также

Примечания

^ Оригинал на французском языке: «le mot permutoèdre est barbare, mais il est facile à retenir; soumettons-le aux crisiques des lecteurs».
^ Томас (2006).
^ Гайха и Гупта (1977).
^ Lancia (2018), п. 105 (см. Главу Пермутаэдр ).
^ См., Например, Зиглер (1995), п. 18.
^ Зиглер (1995), п. 200.
^ Эта разметка графа Кэли показана, например, как Зиглер (1995).
^ Пэк, Чонмин; Адамс, Эндрю (2009). «Некоторые полезные свойства пермутоэдральной решетки для гауссовой фильтрации» (PDF). Tech. Представитель. Стэндфордский Университет.

дальнейшее чтение

Le Conte de Poly-Barbut, Cl. (1990), "Le diagramme du treillis permutoèdre est crossction des diagrammes de deux produits directs d'ordres totaux", Математика, информатика и человеческие науки, 112: 49–53.
Сантмайер, Джо (2007), «На всех возможных расстояниях посмотрите на пермутоэдр», Математический журнал, 80 (2): 120–125, Дои:10.1080 / 0025570X.2007.11953465

внешняя ссылка

Брайан Джейкобс. «Пермутоэдр». MathWorld.
Александр Постников (2005). «Пермутоэдры, ассоциаэдры и не только». arXiv:math.CO/0507163.

[1] Оригинал на французском языке: «le mot permutoèdre est barbare, mais il est facile à retenir; soumettons-le aux crisiques des lecteurs».

[2] Томас (2006).

[3] Гайха и Гупта (1977).

[4] Lancia (2018), п. 105 (см. Главу Пермутаэдр ).

[zface-5] См., Например, Зиглер (1995), п. 18.

[6] Зиглер (1995), п. 200.

[7] Эта разметка графа Кэли показана, например, как Зиглер (1995).

[8] Пэк, Чонмин; Адамс, Эндрю (2009). «Некоторые полезные свойства пермутоэдральной решетки для гауссовой фильтрации» (PDF). Tech. Представитель. Стэндфордский Университет.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]