Тетраэдрическая призма - Tetrahedral prism
| Тетраэдрическая призма | |
|---|---|
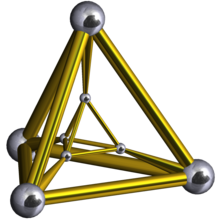 Диаграмма Шлегеля | |
| Тип | Призматический однородный 4-многогранник |
| Единый индекс | 48 |
| Символ Шлефли | {3,3} × {} = h {4,3} × {} с {2,4} × {} sr {2,2} × {} |
| Диаграмма Кокстера | |
| Клетки | 2 (3.3.3 ) 4 (3.4.4 ) |
| Лица | 8 {3} 6 {4} |
| Края | 16 |
| Вершины | 8 |
| Конфигурация вершины | 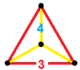 Равносторонний-треугольная пирамида |
| Группа симметрии | [3,3,2], порядок 48 [4,2+, 2], порядок 16 [(2,2)+, 2], порядок 8 |
| Характеристики | выпуклый |
 Сеть | |
В геометрия, а тетраэдрическая призма выпуклый равномерный 4-многогранник. В этом 4-многограннике 6 многогранник ячеек: 2 тетраэдры соединены 4 треугольные призмы. У него 14 граней: 8 треугольных и 6 квадратных. У него 16 ребер и 8 вершин.
Это одна из 18 однородных многогранных призм, созданных с помощью призмы для соединения пар параллельно Платоновы тела и Архимедовы тела.
Изображений
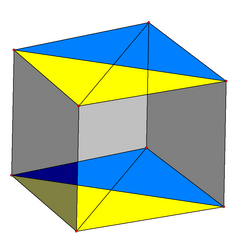 An орфографическая проекция показывает пару параллельных тетраэдров в виде четырехугольника, разделенного на желтые и синие треугольные грани. У каждого тетраэдра также есть два других неокрашенных треугольника на противоположной диагонали. |  Прозрачный Диаграмма Шлегеля виден как один тетраэдр, вложенный внутрь другого, с четырьмя треугольными призмами между парами треугольных граней. |  Вращение в 2-х разных плоскостях |
Альтернативные названия
- Тетраэдрическая диадическая призма (Норман В. Джонсон )
- Тепе (Джонатан Бауэрс: для четырехгранной призмы)
- Тетраэдрическая гиперпризма
- Дигональная антипризматическая призма
- Дигональная антипризматическая гиперпризма
Структура
Тетраэдрическая призма ограничена двумя тетраэдрами и четырьмя треугольными призмами. Треугольные призмы соединены друг с другом своими квадратными гранями и соединены с двумя тетраэдрами своими треугольными гранями.
Прогнозы
Ортографическая проекция тетраэдральной призмы в трехмерное пространство с ориентацией на тетраэдр имеет огибающую тетраэдрической проекции. Обе тетраэдрические ячейки выступают на этот тетраэдр, а треугольные призмы - на его грани.
Ортографическая проекция тетраэдрической призмы в трехмерное пространство с ориентацией на треугольную призму имеет огибающую проекции в форме треугольной призмы. Две тетраэдрические ячейки проецируются на треугольные концы призмы, каждая из которых имеет вершину, которая выступает в центр соответствующей треугольной грани. Ребро соединяет эти две вершины через центр выступа. Призма может быть разделена на три неоднородные треугольные призмы, которые встречаются на этом краю; эти 3 тома соответствуют изображениям трех из четырех треугольных призматических ячеек. Последняя треугольная призматическая ячейка проецируется на всю огибающую проекции.
Ортографическая проекция тетраэдральной призмы в трехмерное пространство вперед с ребра идентична ее параллельной проекции с ориентацией на треугольную призму.
Ортографическая проекция тетраэдрической призмы с квадратной гранью вперед в трехмерное пространство имеет кубоидальную оболочку (см. Диаграмму). Каждая треугольная призматическая ячейка проецируется на половину кубоидального объема, образуя две пары перекрывающихся изображений. Тетраэдрические ячейки выступают на верхнюю и нижнюю квадратные грани кубоида.
Связанные многогранники
Это первая из бесконечной серии однородные антипризматические призмы.
| имя | с {2,2} × {} | с {2,3} × {} | с {2,4} × {} | с {2,5} × {} | с {2,6} × {} | с {2,7} × {} | с {2,8} × {} | s {2, p} × {} |
|---|---|---|---|---|---|---|---|---|
| Coxeter диаграмма | ||||||||
| Образ |  |  |  |  |  |  |  |  |
| Вершина фигура |  |  | ||||||
| Клетки | 2 с {2,2} (2) {2}×{}={4} 4 {3}×{} | 2 с {2,3} 2 {3}×{} 6 {3}×{} | 2 с {2,4} 2 {4}×{} 8 {3}×{} | 2 с {2,5} 2 {5}×{} 10 {3}×{} | 2 с {2,6} 2 {6}×{} 12 {3}×{} | 2 с {2,7} 2 {7}×{} 14 {3}×{} | 2 с {2,8} 2 {8}×{} 16 {3}×{} | 2 с {2, p} 2 {p} × {} 2п {3}×{} |
| Сеть |  |  |  |  |  |  |  |  |
Тетраэдрическая призма, -131, является первым в серии размерностей однородных многогранников, выражаемых Coxeter просить31 серии. Тетраэдрическая призма является вершиной для второй, выпрямленный 5-симплексный. Пятая фигура - евклидовы соты, 331, а финал - некомпактные гиперболические соты, 431. Каждый равномерный многогранник в последовательности вершина фигуры следующего.
| п | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| Coxeter группа | А3А1 | А5 | D6 | E7 | = E7+ | = E7++ |
| Coxeter диаграмма | ||||||
| Симметрия | [3−1,3,1] | [30,3,1] | [31,3,1] | [32,3,1] | [33,3,1] | [34,3,1] |
| порядок | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| График |  |  |  |  | - | - |
| имя | −131 | 031 | 131 | 231 | 331 | 431 |
использованная литература
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26)
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
внешняя ссылка
- 6. Выпуклая однородная призматическая полихора - Модель 48., Георгий Ольшевский.
- Клитцинг, Ричард. «4D однородные многогранники (полихоры) x x3o3o - тепе».


