Дуопризма - Duoprism
| Набор униформ p-q дуопризм | |
| Тип | Призматические однородные 4-многогранники |
| Символ Шлефли | {p} × {q} |
| Диаграмма Кокстера-Дынкина | |
| Клетки | p q-gonal призмы, q p-угольные призмы |
| Лица | pq квадраты, p q-угольники, q p-угольников |
| Края | 2pq |
| Вершины | pq |
| Фигура вершины |  дисфеноид |
| Симметрия | [p, 2, q], порядок 4pq |
| Двойной | п-д дуопирамида |
| Характеристики | выпуклый, вершинно-однородный |
| Набор форменных p-p дуопризм | |
| Тип | Призматический однородный 4-многогранник |
| Символ Шлефли | {p} × {p} |
| Диаграмма Кокстера-Дынкина | |
| Клетки | 2p п-угольный призмы |
| Лица | п2 квадраты, 2p p-угольники |
| Края | 2p2 |
| Вершины | п2 |
| Симметрия | [[p, 2, p]] = [2p, 2+, 2п], порядок 8п2 |
| Двойной | п-п дуопирамида |
| Характеристики | выпуклый, вершинно-однородный, Фасетно-переходный |

В геометрия 4-х измерений или выше, дуопризма это многогранник в результате Декартово произведение двух многогранников, каждый из которых имеет два или более размера. Декартово произведение п-полигон и м-политоп - это (п+м) -многогранник, где п и м 2 (многоугольник ) или выше.
Самая низкая размерность дуопризма существуют в 4-мерном пространстве как 4-многогранники будучи Декартово произведение из двух полигоны в 2-х мерном Евклидово пространство. Точнее, это набор баллов:
куда п1 и п2 - это множества точек, содержащихся в соответствующих многоугольниках. Такая дуопризма - это выпуклый если оба основания выпуклые и ограничены призматические ячейки.
Номенклатура
Четырехмерные дуопризмы считаются призматическими 4-многогранниками. Дуопризма, построенная из двух правильные многоугольники такой же длины кромки - это однородная дуопризма.
Дуопризма из п-полигоны и м-полигоны именуются префиксом «дуопризма» с именами базовых многоугольников, например: a треугольно-пятиугольная дуопризма - декартово произведение треугольника и пятиугольника.
Альтернативный, более краткий способ определения конкретной дуопризмы - это префикс цифрами, обозначающими базовые многоугольники, например: 3,5-дуопризма для треугольно-пятиугольной дуопризмы.
Другие альтернативные названия:
- q-гональный-п-угольная призма
- q-гональный-п-угольная двойная призма
- q-гональный-п-гональная гиперпризма
Период, термин дуопризма придуман Георгием Ольшевским, сокращенно от двойная призма. Джон Хортон Конвей предложил похожее название пропризма за призма продукта, декартово произведение двух или более многогранников размерности не менее двух. Дуопризма - это пропризмы, образованные ровно из двух многогранников.
Пример 16-16 дуопризма.
Диаграмма Шлегеля Показаны проекции из центра одной 16-угольной призмы и всех, кроме одной, противоположных 16-угольных призм. | сеть Показаны два набора 16-угольных призм. Верхняя и нижняя грани вертикали цилиндр соединяются в сложенном виде в 4D. |
Геометрия 4-х мерных дуопризм
4-х мерный униформа дуопризма создается продуктом обычного п-сторонний многоугольник и регулярный м-сторонний многоугольник с одинаковой длиной ребра. Он ограничен п м-гональный призмы и м п-угольные призмы. Например, декартово произведение треугольника и шестиугольника - это дуопризма, ограниченная 6 треугольными призмами и 3 шестиугольными призмами.
- Когда м и п идентичны, результирующая дуопризма ограничена 2п идентичный п-угольные призмы. Например, декартово произведение двух треугольников - это дуопризма, ограниченная 6 треугольными призмами.
- Когда м и п равны 4 тождественно, то полученная дуопризма ограничена 8 квадратными призмами (кубики ) и идентичен тессеракт.
В м-угольные призмы прикреплены друг к другу своими м-угольные грани и образуют замкнутый контур. Точно так же п-угольные призмы прикреплены друг к другу своими п-угольные грани и образуют вторую петлю, перпендикулярную первой. Эти две петли прикреплены друг к другу квадратными гранями и взаимно перпендикулярны.
В качестве м и п приближаются к бесконечности, соответствующие дуопризмы приближаются к дуоцилиндр. Таким образом, дуопризмы полезны как неквадрика приближения дуоцилиндра.
Сети
 3-3 |  4-4 | 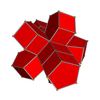 5-5 |  6-6 |  8-8 |  10-10 |
 3-4 |  3-5 | 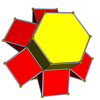 3-6 | 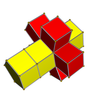 4-5 | 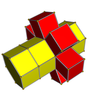 4-6 | 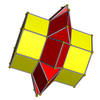 3-8 |
Перспективные прогнозы
Перспективная проекция с центром в ячейке делает дуопризму похожей на тор, с двумя наборами ортогональных ячеек, p-угольными и q-угольными призмами.
 |  |
| 6-призма | 6-6 дуопризма |
|---|---|
| А шестиугольная призма, спроецированный на плоскость в перспективе, с центром на шестиугольной грани, выглядит как двойной шестиугольник, соединенный (искаженный) квадраты. Точно так же 6-6 дуопризма, проецируемая в 3D, приблизительно равна тор, шестиугольная как в плане, так и в разрезе. | |
Дуопризмы p-q идентичны дуопризмам q-p, но выглядят в этих проекциях по-разному, потому что они проецируются в центре разных клеток.
 3-3 |  3-4 |  3-5 |  3-6 |  3-7 |  3-8 |
 4-3 |  4-4 |  4-5 |  4-6 |  4-7 |  4-8 |
 5-3 |  5-4 |  5-5 |  5-6 |  5-7 |  5-8 |
 6-3 |  6-4 |  6-5 |  6-6 |  6-7 |  6-8 |
 7-3 |  7-4 |  7-5 |  7-6 |  7-7 |  7-8 |
 8-3 |  8-4 |  8-5 |  8-6 |  8-7 |  8-8 |
Ортогональные проекции
Вершинно-центрированные ортогональные проекции p-p дуопризм проецируются в симметрию [2n] для нечетных степеней и [n] для четных степеней. В центр проецируются n вершин. Для 4,4 он представляет собой A3 Самолет Кокстера тессеракт. Проекция 5,5 идентична 3D ромбический триаконтаэдр.
| Странный | |||||||
|---|---|---|---|---|---|---|---|
| 3-3 | 5-5 | 7-7 | 9-9 | ||||
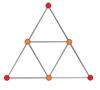 |  | 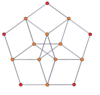 | 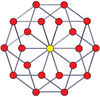 | 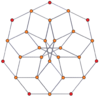 |  | 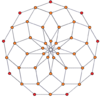 | 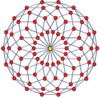 |
| [3] | [6] | [5] | [10] | [7] | [14] | [9] | [18] |
| Четное | |||||||
| 4-4 (тессеракт) | 6-6 | 8-8 | 10-10 | ||||
 |  | 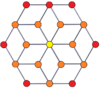 | 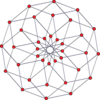 | 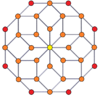 |  | 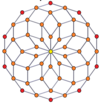 |  |
| [4] | [8] | [6] | [12] | [8] | [16] | [10] | [20] |
Связанные многогранники

В правильный косой многогранник, {4,4 | n}, существует в 4-пространстве как n2 квадратные грани n-n дуопризма, используя все 2n2 края и п2 вершины. 2п п-гональные грани можно увидеть как удаленные. (косые многогранники можно увидеть точно так же через n-m дуопризму, но это не обычный.)
Дуоантипризма


Словно антипризмы как чередование призмы, существует набор 4-х мерных дуоантипризм: 4-многогранники которые могут быть созданы чередование операция применительно к дуопризме. Чередующиеся вершины создают нерегулярные тетраэдрические ячейки, за исключением особого случая, 4-4 дуопризма (тессеракт ), который создает равномерную (и регулярную) 16 ячеек. 16-ячеечная - единственная выпуклая однородная дуоантипризма.
Дуопризма ![]()
![]()
![]()
![]()
![]()
![]()
![]() , т0,1,2,3{p, 2, q}, можно заменить на
, т0,1,2,3{p, 2, q}, можно заменить на ![]()
![]()
![]()
![]()
![]()
![]()
![]() , ht0,1,2,3{p, 2, q}, «дуоантипризмы», которые в целом нельзя сделать единообразными. Единственное выпуклое равномерное решение - это тривиальный случай p = q = 2, который является конструкцией нижней симметрии тессеракт
, ht0,1,2,3{p, 2, q}, «дуоантипризмы», которые в целом нельзя сделать единообразными. Единственное выпуклое равномерное решение - это тривиальный случай p = q = 2, который является конструкцией нижней симметрии тессеракт ![]()
![]()
![]()
![]()
![]()
![]()
![]() , т0,1,2,3{2,2,2}, с его чередованием как 16 ячеек,
, т0,1,2,3{2,2,2}, с его чередованием как 16 ячеек, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , с {2} с {2}.
, с {2} с {2}.
Единственное невыпуклое равномерное решение - p = 5, q = 5/3, ht0,1,2,3{5,2,5/3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , построенный из 10 пятиугольные антипризмы, 10 пентаграмматические скрещенные антипризмы, и 50 тетраэдров, известных как большой дуоантипризм (гудап).[1][2]
, построенный из 10 пятиугольные антипризмы, 10 пентаграмматические скрещенные антипризмы, и 50 тетраэдров, известных как большой дуоантипризм (гудап).[1][2]
Дитетраголтриаты
Также связаны дитетрагольтриаты или октагольтриаты, образованные восьмиугольник (считающийся двуугольником или усеченным квадратом) в p-угольник. В восьмиугольник p-угольника можно четко определить, если предположить, что восьмиугольник - это выпуклая оболочка двух перпендикулярных прямоугольники; тогда p-угольный дитетрагольтриат представляет собой выпуклую оболочку двух p-p дуопризм (где p-угольники подобны, но не конгруэнтны, имеют разные размеры) в перпендикулярных ориентациях. Полученный полихорон изогонален, имеет 2p p-угольные призмы и p2 прямоугольные трапеции (a куб с D2d симметрия), но не может быть однородной. Фигура вершины - это треугольная бипирамида.
Двойные антипризмоиды
Как дуоантипризмы как чередующиеся дуопризмы, существует набор p-угольных двойных антипризмоидов, созданных чередованием 2p-угольных дитетраголтриатов, созданием p-гональных антипризм и тетраэдров, одновременно интерпретируя некореальмические треугольные бипирамидные пространства как два тетраэдра. Результирующая цифра обычно неоднородна, за исключением двух случаев: великая антипризма и его конъюгат, пентаграмматический двойной антипризмоид (с p = 5 и 5/3 соответственно), представленный как чередование декагонального или декаграмматического дитетраголтриата. Фигура вершины - это вариант сфенокорона.
k_22 многогранники
В 3-3 дуопризма, -122, является первым в размерной серии однородных многогранников, выражаемой Coxeter просить22 серии. Дуопризма 3-3 - это вершина для второго, двуатомный 5-симплексный. Четвертая фигура - евклидовы соты, 222, а финал - паракомпактные гиперболические соты, 322, с группой Кокстера [32,2,3], . Каждый прогрессивный равномерный многогранник построен из предыдущего, поскольку его вершина фигура.
| Космос | Конечный | Евклидово | Гиперболический | ||
|---|---|---|---|---|---|
| п | 4 | 5 | 6 | 7 | 8 |
| Coxeter группа | А2А2 | E6 | = E6+ | = E6++ | |
| Coxeter диаграмма | |||||
| Симметрия | [[32,2,-1]] | [[32,2,0]] | [[32,2,1]] | [[32,2,2]] | [[32,2,3]] |
| Заказ | 72 | 1440 | 103,680 | ∞ | |
| График |  |  |  | ∞ | ∞ |
| Имя | −122 | 022 | 122 | 222 | 322 |
Смотрите также
Примечания
- ^ Джонатан Бауэрс - Разная униформа Полихора 965. Гудап
- ^ http://www.polychora.com/12GudapsMovie.gif Анимация сечений
Рекомендации
- Правильные многогранники, Х. С. М. Коксетер, Dover Publications, Inc., 1973, Нью-Йорк, стр. 124.
- Coxeter, Красота геометрии: двенадцать эссе, Dover Publications, 1999 г., ISBN 0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги)
- Кокстер, Х. С. М. Правильные косые многогранники в трех и четырех измерениях. Proc. Лондонская математика. Soc. 43, 33-62, 1937.
- Простое объяснение четвертого измерения, Генри П. Мэннинг, Munn & Company, 1910, Нью-Йорк. Доступно в библиотеке Университета Вирджинии. Также доступны онлайн: Простое объяснение четвертого измерения - содержит описание дуопризм (двойных призм) и дуоцилиндров (двойных цилиндров). Googlebook
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.



