Пентаграмматическая скрещенная антипризма - Pentagrammic crossed-antiprism
Эта статья нужны дополнительные цитаты для проверка. (Декабрь 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Униформа пентаграмматическая скрещенная антипризма | |
|---|---|
 | |
| Тип | Призматический однородный многогранник |
| Элементы | F = 12, E = 20 V = 10 (χ = 2) |
| Лица по сторонам | 10{3}+2{5/2} |
| Символ Шлефли | с {2,10/3} sr {2,5/3} |
| Символ Wythoff | | 2 2 5/3 |
| Диаграмма Кокстера | = |
| Симметрия | D5ч, [5,2], (* 522), порядок 20 |
| Группа вращения | D5, [5,2]+, (552), заказ 10 D5d |
| Указатель ссылок | U80 (а) |
| Двойной | Пентаграмматический вогнутый трапецоэдр |
| Характеристики | невыпуклый |
 Фигура вершины 3.3.3.5/3 или 3.3.3.-5/2 | |

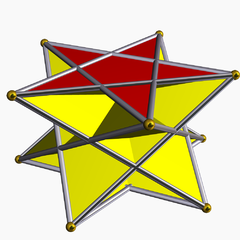
Трехмерная модель (единой) пентаграммы скрещенной антипризмы.
В геометрия, то пентаграмматическая скрещенная антипризма один в бесконечном множестве невыпуклых антипризмы образованный сторонами треугольника и двумя правильными звездный многоугольник колпачки, в данном случае два пентаграммы.
Он отличается от пентаграммическая антипризма имея противоположные ориентации на двух пентаграммах.
Этот многогранник обозначается индексированным именем U80 как равномерный многогранник.
 Альтернативное представление с полыми пентаграммами. |
Пентаграмматическая скрещенная антипризма может быть вписана в икосаэдр, и имеет десять треугольных граней, общих с большой икосаэдр. Он имеет то же самое расположение вершин как пятиугольная антипризма. Фактически, это можно рассматривать как парабидоусиленный большой икосаэдр.
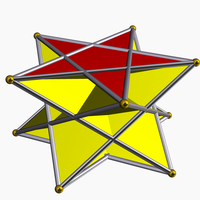 Пентаграмматическая скрещенная антипризма |  Большой икосаэдр окрашен D5d симметрия |
Смотрите также
внешняя ссылка
- Вайсштейн, Эрик В. «Пентаграмматическая скрещенная антипризма». MathWorld.
- http://www.mathconsult.ch/showroom/unipoly/80.html
- http://bulatov.org/polyhedra/uniform/u05.html
- https://web.archive.org/web/20050313234519/http://www.math.technion.ac.il/~rl/kaleido/data/05.html
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
