Додекаэдрические соты порядка 5 - Википедия - Order-5 dodecahedral honeycomb

Додекаэдрические соты порядка 5
Перспективная проекция Посмотреть из центра Модель диска Пуанкаре
Тип	Гиперболические обычные соты Равномерные гиперболические соты
Символ Шлефли	{5,3,5}
Диаграмма Кокстера-Дынкина
Клетки	{5,3}
Лица	пятиугольник {5}
Край фигура	пятиугольник {5}
Фигура вершины	икосаэдр
Двойной	Самодвойственный
Группа Кокстера	${ displaystyle { overline {K}} _ {3}}$ , [5,3,5]
Характеристики	Обычный

В додекаэдрические соты порядка 5 один из четырех компактных обычный заполнение пространства мозаика (или же соты ) в гиперболическое 3-пространство. С Символ Шлефли {5,3,5}, в нем пять додекаэдр ячеек вокруг каждого ребра, а каждая вершина окружена двадцатью додекаэдрами. Его вершина фигуры является икосаэдр.

А геометрические соты это заполнение пространства из многогранник или многомерный клетки, чтобы не было зазоров. Это пример более общего математического черепица или же мозаика в любом количестве измерений.

Соты обычно строятся из обычных Евклидово ("плоское") пространство, как и выпуклые однородные соты. Они также могут быть построены в неевклидовы пространства, Такие как гиперболические однородные соты. Любой конечный равномерный многогранник можно спроецировать на его окружающая сфера образовывать однородные соты в сферическом пространстве.

Описание

В двугранный угол евклидова правильный додекаэдр составляет ~ 116,6 °, поэтому не более трех из них могут поместиться вокруг края в евклидовом трехмерном пространстве. Однако в гиперболическом пространстве двугранный угол меньше, чем в евклидовом пространстве, и зависит от размера фигуры; наименьший возможный двугранный угол составляет 60 ° для идеального гиперболического правильного додекаэдра с бесконечно длинными ребрами. В додекаэдр в этой додекаэдрической соте размер всех двугранных углов равен 72 °.

Изображений

Это аналог 2D гиперболического пятиугольная черепица порядка 5, {5,5}

Связанные многогранники и соты

В трехмерном гиперболическом пространстве есть четыре регулярных компактных соты:

Четыре обычных компактных соты в H³
{5,3,4}	{4,3,5}	{3,5,3}	{5,3,5}

В трехмерном гиперболическом пространстве есть еще одна сота, называемая додекаэдрические соты порядка 4, {5,3,4}, у которого только четыре додекаэдра на ребро. Эти соты также относятся к 120 ячеек который можно рассматривать как соты в положительно искривленном пространстве (поверхность 4-мерной сферы) с тремя додекаэдрами на каждом ребре, {5,3,3}. Наконец додекаэдр дитоп, {5,3,2} существует на 3-сфера, с 2-мя полусферическими ячейками.

Есть девять однородных сот в [5,3,5] Группа Кокстера семья, включая эту обычную форму. Так же усеченный битами форма, т_1,2{5,3,5}, , в этой соте есть все усеченный икосаэдр клетки.

[5,3,5] семейные соты
{5,3,5}	г {5,3,5}	т {5,3,5}	рр {5,3,5}	т_0,3{5,3,5}

	2т {5,3,5}	тр {5,3,5}	т_0,1,3{5,3,5}	т_0,1,2,3{5,3,5}

В Пространство Зейферта – Вебера это компактный многообразие который может быть сформирован как факторное пространство порядка-5 додекаэдрических сот.

Эти соты являются частью последовательности полихор и сот с икосаэдр фигуры вершин:

{p, 3,5} многогранники
Космос	S³	ЧАС³
Форма	Конечный	Компактный		Паракомпакт	Некомпактный
Имя	{3,3,5}	{4,3,5}	{5,3,5}	{6,3,5}	{7,3,5}	{8,3,5}	... {∞,3,5}
Изображение
Клетки	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Эти соты являются частью последовательности правильных многогранников и сот с додекаэдр клетки:

{5,3, p} многогранники
Космос	S³	ЧАС³
Форма	Конечный	Компактный		Паракомпакт	Некомпактный
Имя	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	... {5,3,∞}
Изображение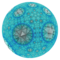
Вершина фигура	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

{p, 3, p} обычные соты
Космос	S³	Евклидово E³	ЧАС³
Форма	Конечный	Аффинный	Компактный	Паракомпакт	Некомпактный
Имя	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Изображение
Клетки	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Вершина фигура	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Выпрямленные додекаэдрические соты порядка 5

Выпрямленные додекаэдрические соты порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	г {5,3,5}
Диаграмма Кокстера
Клетки	г {5,3} {3,5}
Лица	треугольник {3} пятиугольник {5}
Фигура вершины	пятиугольная призма
Группа Кокстера	${ displaystyle { overline {K}} _ {3}}$ , [5,3,5]
Характеристики	Вершинно-транзитивный, реберный транзитивный

В выпрямленные додекаэдрические соты порядка 5, , имеет чередующиеся икосаэдр и икосододекаэдр ячейки, с пятиугольная призма вершина фигуры.

Связанные плитки и соты

Его можно рассматривать как аналог двумерного гиперболического Пятиугольная черепица порядка 4, г {5,5}

Всего существует четыре выпрямленных компактных обычных соты:

Четыре выпрямленных обычных компактных сот в H³
Изображение
Символы	г {5,3,4}	г {4,3,5}	г {3,5,3}	г {5,3,5}
Вершина фигура

г {р, 3,5}
Космос	S³	ЧАС³
Форма	Конечный	Компактный		Паракомпакт	Некомпактный
Имя	г {3,3,5}	г {4,3,5}	г {5,3,5}	г {6,3,5}	г {7,3,5}	... г {∞, 3,5}
Изображение
Клетки {3,5}	г {3,3}	г {4,3}	г {5,3}	г {6,3}	г {7,3}	г {∞, 3}

Усеченные додекаэдрические соты порядка 5

Усеченные додекаэдрические соты порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т {5,3,5}
Диаграмма Кокстера
Клетки	т {5,3} {3,5}
Лица	треугольник {3} десятиугольник {10}
Фигура вершины	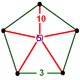пятиугольная пирамида
Группа Кокстера	${ displaystyle { overline {K}} _ {3}}$ , [5,3,5]
Характеристики	Вершинно-транзитивный

В усеченная додекаэдрическая сотовая структура порядка 5, , имеет икосаэдр и усеченный додекаэдр ячейки, с пятиугольная пирамида вершина фигуры.

Связанные соты

Четыре усеченных обычных компактных сот в H³
Изображение
Символы	т {5,3,4}	т {4,3,5}	т {3,5,3}	т {5,3,5}
Вершина фигура

Додекаэдрические соты с усеченной структурой порядка 5

Додекаэдрические соты с усеченной структурой порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	2т {5,3,5}
Диаграмма Кокстера
Клетки	т {3,5}
Лица	пятиугольник {5} шестиугольник {6}
Фигура вершины	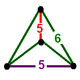тетрагональный дисфеноид
Группа Кокстера	${ displaystyle 2 times { overline {K}} _ {3}}$ , [[5,3,5]]
Характеристики	Вершинно-транзитивный, реберный, клеточно-транзитивный

В додекаэдрические соты с усеченным битом порядка 5, , имеет усеченный икосаэдр ячейки, с тетрагональный дисфеноид вершина фигуры.

Связанные соты

Три усеченных компактной соты в H³
Изображение
Символы	2т {4,3,5}	2т {3,5,3}	2т {5,3,5}
Вершина фигура

Додекаэдрические соты с разводкой порядка 5

Додекаэдрические соты с разводкой порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	рр {5,3,5}
Диаграмма Кокстера
Клетки	рр {5,3} г {3,5} {} x {5}
Лица	треугольник {3} квадрат {4} пятиугольник {5}
Фигура вершины	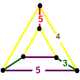клин
Группа Кокстера	${ displaystyle { overline {K}} _ {3}}$ , [5,3,5]
Характеристики	Вершинно-транзитивный

В скошенные додекаэдрические соты порядка 5, , имеет ромбикосододекаэдр, икосододекаэдр, и пятиугольная призма ячейки, с клин вершина фигуры.

Связанные соты

Четыре скошенных регулярных компактных сот в H³

Изображение
Символы	рр {5,3,4}	рр {4,3,5}	рр {3,5,3}	рр {5,3,5}
Вершина фигура

Cantitruncated додекаэдрические соты порядка 5

Cantitruncated додекаэдрические соты порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	тр {5,3,5}
Диаграмма Кокстера
Клетки	tr {5,3} т {3,5} {} x {5}
Лица	квадрат {4} пятиугольник {5} шестиугольник {6} десятиугольник {10}
Фигура вершины	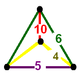зеркальная клиновидная кость
Группа Кокстера	${ displaystyle { overline {K}} _ {3}}$ , [5,3,5]
Характеристики	Вершинно-транзитивный

В усеченные додекаэдрические соты порядка 5, , имеет усеченный икосододекаэдр, усеченный икосаэдр, и пятиугольная призма ячейки, с зеркальная клиновидная кость вершина фигуры.

Связанные соты

Четыре усеченных обычных компактных сот в H³
Изображение
Символы	tr {5,3,4}	tr {4,3,5}	tr {3,5,3}	тр {5,3,5}
Вершина фигура

Додекаэдрические соты Runcinated порядка 5

Додекаэдрические соты Runcinated порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т_0,3{5,3,5}
Диаграмма Кокстера
Клетки	{5,3} {} x {5}
Лица	квадрат {4} пятиугольник {5}
Фигура вершины	треугольная антипризма
Группа Кокстера	${ displaystyle 2 times { overline {K}} _ {3}}$ , [[5,3,5]]
Характеристики	Вершинно-транзитивный, реберный транзитивный

В додекаэдрические соты типа runcinated-5, , имеет додекаэдр и пятиугольная призма ячейки, с треугольная антипризма вершина фигуры.

Связанные соты

Три плоских регулярных компактных соты в H³
Изображение
Символы	т_0,3{4,3,5}	т_0,3{3,5,3}	т_0,3{5,3,5}
Вершина фигура

Усеченная додекаэдрическая сотовая структура порядка 5

Усеченная додекаэдрическая сотовая структура порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т_0,1,3{5,3,5}
Диаграмма Кокстера
Клетки	т {5,3} рр {5,3} {} x {5} {} x {10}
Лица	треугольник {3} квадрат {4} пятиугольник {5} десятиугольник {10}
Фигура вершины	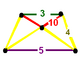равнобедренно-трапециевидный пирамида
Группа Кокстера	${ displaystyle { overline {K}} _ {3}}$ , [5,3,5]
Характеристики	Вершинно-транзитивный

В усеченная додекаэдрическая сотовая структура порядка 5, , имеет усеченный додекаэдр, ромбикосододекаэдр, пятиугольная призма, и десятиугольная призма ячейки, с равнобедренно-трапециевидный пирамида вершина фигуры.

В додекаэдрические соты с разветвленной звездочкой порядка 5 эквивалентна усеченной додекаэдрической соте пятого порядка.

Связанные соты

Четыре ряда усеченных обычных компактных сот в H³


Изображение
Символы	т_0,1,3{5,3,4}	т_0,1,3{4,3,5}	т_0,1,3{3,5,3}	т_0,1,3{5,3,5}
Вершина фигура

Всенаправленные додекаэдрические соты порядка 5

Всенаправленные додекаэдрические соты порядка 5
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т_0,1,2,3{5,3,5}
Диаграмма Кокстера
Клетки	tr {5,3} {} x {10}
Лица	квадрат {4} шестиугольник {6} десятиугольник {10}
Фигура вершины	филлический дисфеноид
Группа Кокстера	${ displaystyle 2 times { overline {K}} _ {3}}$ , [[5,3,5]]
Характеристики	Вершинно-транзитивный