Многообразие - Manifold

В реальная проективная плоскость представляет собой двумерное многообразие, которое не может быть реализовано в трех измерениях без самопересечения, показанное здесь как Поверхность мальчика.

Поверхность Земли требует (как минимум) двух карт для включения каждой точки. Здесь глобус раскладывается на диаграммы вокруг к северу и Южные полюса.

В математика, а многообразие это топологическое пространство что локально напоминает Евклидово пространство возле каждой точки. Точнее, $п$ -мерное многообразие, или $п$ -многообразие для краткости, это топологическое пространство со свойством, что каждая точка имеет район то есть гомеоморфный в евклидово пространство размерности $п$ .

Одномерные многообразия включают линии и круги, но нет восьмерки (поскольку никакая окрестность их точки пересечения не гомеоморфна евклидову 1-пространству). Двумерные многообразия также называют поверхности. Примеры включают самолет, то сфера, а тор, которые все могут быть встроенный (сформированный без самопересечений) в трехмерном реальном пространстве, но также Бутылка Клейна и реальная проективная плоскость, которые всегда будут самопересекаться, когда погруженный в трехмерном реальном пространстве.

Хотя многообразие локально напоминает евклидово пространство, что означает, что каждая точка имеет окрестность, гомеоморфную открытому подмножеству евклидова пространства, глобально оно может не быть гомеоморфным евклидову пространству. Например, поверхность сфера не гомеоморфен Евклидова плоскость, потому что (среди других свойств) он обладает глобальным топологическим свойством компактность что евклидово пространство отсутствует, но в регионе его можно нанести на карту с помощью картографические проекции области на евклидову плоскость (в контексте многообразий они называются графики ). Когда регион появляется в двух соседних диаграммах, два представления не совпадают в точности, и для перехода от одного к другому требуется преобразование, называемое карта перехода.

Концепция многообразия занимает центральное место во многих частях геометрия и современный математическая физика потому что он позволяет описывать и понимать сложные структуры в терминах более простых локальных топологических свойств евклидова пространства. Многообразия естественно возникают как множества решений системы уравнений и, как графики функций.

Коллекторы могут быть оснащены дополнительной конструкцией. Одним из важных классов многообразий является класс дифференцируемые многообразия; это дифференцируемая структура позволяет исчисление будет сделано на коллекторах. А Риманова метрика на коллекторе позволяет расстояния и углы быть измеренным. Симплектические многообразия служить фазовые пространства в Гамильтонов формализм из классическая механика, а четырехмерный Лоренцевы многообразия модель пространство-время в общая теория относительности.

Мотивирующие примеры

Поверхность - это двумерное многообразие, что означает, что она локально напоминает евклидову плоскость около каждой точки. Например, поверхность земного шара может быть описана набором карт (называемых диаграммами), которые вместе образуют атлас земного шара. Хотя для покрытия всей поверхности земного шара отдельной карты недостаточно, любое место на земном шаре будет хотя бы на одной из карт.

Многие места появятся более чем на одной диаграмме. Например, карта Северная Америка вероятно будет включать части Южная Америка и Полярный круг. Эти регионы земного шара будут полностью описаны в отдельных диаграммах, которые, в свою очередь, будут содержать части Северной Америки. Между соседними диаграммами существует связь, называемая карта перехода что позволяет последовательно соединять их вместе для покрытия всего земного шара.

Описание координатных диаграмм на поверхностях явно требует знания функций двух переменных, потому что эти функции исправления должны отображать область на плоскости в другую область плоскости. Однако одномерные примеры многообразий (или кривых) можно описать функциями только одной переменной.

У коллекторов есть приложения в компьютерной графике и дополненной реальности, учитывая необходимость связывания изображений (текстуры) с координатами (например, компьютерной томографии). В настройках дополненной реальности изображение (касательная плоскость) можно рассматривать как нечто, связанное с координатами и Используя датчики для обнаружения движений и вращения, можно узнать, как изображение ориентировано и размещено в пространстве.

Круг

Рисунок 1: Каждая из четырех диаграмм отображает часть круга на открытый интервал и вместе покрывает весь круг.

После строки круг является простейшим примером топологического многообразия. Топология игнорирует изгиб, поэтому маленький кусок круга обрабатывается точно так же, как маленький кусок линии. Рассмотрим, например, верхнюю часть единичный круг, Икс² + у² = 1, где у-координат положительный (обозначен желтой дугой окружности в Рисунок 1). Любую точку этой дуги можно однозначно описать своим Икс-координат. Так, проекция на первую координату непрерывный, и обратимый, отображение от верхней дуги к открытый интервал (−1, 1):

{ Displaystyle чи _ { mathrm {сверху}} (х, у) = х. ,}

Такие функции вместе с открытыми регионами, которые они отображают, называются графики. Точно так же есть диаграммы для нижней (красной), левой (синей) и правой (зеленой) частей круга:

{ displaystyle { begin {align} chi _ { mathrm {bottom}} (x, y) & = x chi _ { mathrm {left}} (x, y) & = y чи _ { mathrm {right}} (х, у) & = у. конец {выровнено}}}

Вместе эти части покрывают весь круг, а четыре диаграммы образуют атлас для круга.

Верхний и правый графики, ${ displaystyle chi _ { mathrm {top}}}$ и ${ displaystyle chi _ { mathrm {right}}}$ соответственно, перекрываются в своей области: их пересечение лежит в той четверти круга, где оба ${ displaystyle x}$ - и ${ displaystyle y}$ -координаты положительные. Каждая отображает эту часть в интервал ${ displaystyle (0,1)}$ Хотя по-другому. Таким образом, функция ${ displaystyle T: (0,1) rightarrow (0,1) = chi _ { mathrm {right}} circ chi _ { mathrm {top}} ^ {- 1}}$ можно построить, который принимает значения из ко-области ${ displaystyle chi _ { mathrm {top}}}$ обратно в круг, используя обратный, за которым следует ${ displaystyle chi _ { mathrm {right}}}$ назад к интервалу. Позволять а быть любым числом в ${ displaystyle (0,1)}$ , тогда:

{ Displaystyle { begin {align} T (a) & = chi _ { mathrm {right}} left ( chi _ { mathrm {top}} ^ {- 1} left [a right] right) & = chi _ { mathrm {right}} left (a, { sqrt {1-a ^ {2}}} right) & = { sqrt {1-a ^ {2}}} end {выровнено}}}

Такая функция называется карта перехода.

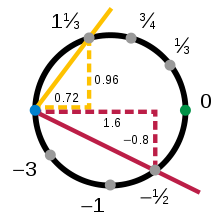
Рисунок 2: Круговая диаграмма многообразия, основанная на наклоне, покрывающая все точки круга, кроме одной.

Верхняя, нижняя, левая и правая диаграммы показывают, что круг является многообразием, но они не образуют единственно возможный атлас. Диаграммы не обязательно должны быть геометрическими проекциями, и количество диаграмм является вопросом выбора. Рассмотрим графики

{ displaystyle chi _ { mathrm {минус}} (x, y) = s = { frac {y} {1 + x}}}

и

{ displaystyle chi _ { mathrm {plus}} (x, y) = t = { frac {y} {1-x}}}

Здесь s - наклон прямой, проходящей через точку с координатами (Икс, у) и неподвижная точка поворота (−1, 0); так же, т противоположен наклону прямой, проходящей через точки с координатами (Икс, у) и (+1, 0). Обратное отображение из s к (Икс, у) дан кем-то

{ displaystyle { begin {align} x & = { frac {1-s ^ {2}} {1 + s ^ {2}}} [5pt] y & = { frac {2s} {1 + s ^ {2}}} конец {выровнено}}}

Нетрудно подтвердить, что Икс² + у² = 1 для всех значений s и т. Эти две диаграммы представляют собой второй атлас для круга с картой перехода.

{ displaystyle t = { frac {1} {s}}}

(то есть существует связь между s и т для каждой точки, где s и т оба ненулевые).

На каждой диаграмме отсутствует одна точка, либо (-1, 0) для s или (+1, 0) для т, поэтому ни одной диаграммы недостаточно, чтобы охватить весь круг. Можно доказать, что невозможно охватить полный круг одной картой. Например, хотя можно построить круг из одного отрезка линии, перекрывая и «склеивая» концы, это не дает диаграммы; часть круга будет отображена на оба конца одновременно, теряя обратимость.

Сфера

В сфера это пример поверхности. В единичная сфера из неявное уравнение

Икс 2 + у 2 + z 2 - 1 = 0

может быть покрыт атласом шести графики: самолет $z = 0$ делит сферу на две полусферы ( $z > 0$ и $z < 0$ ), которые могут быть отображены на диске $Икс 2 + у 2 < 1$ проекцией на $ху$ плоскость координат. Это дает две диаграммы; четыре других диаграммы представлены аналогичной конструкцией с двумя другими координатными плоскостями.

Что касается круга, можно определить одну карту, которая покрывает всю сферу, за исключением одной точки. Таким образом, достаточно двух карт, но сфера не может быть покрыта одной картой.

Этот пример исторически значим, так как он послужил основой для терминологии; стало очевидно, что вся поверхность земной шар не может иметь плоское представление, состоящее из одного карта (также называется "диаграммой", см. морская карта ), и поэтому требуется атласы для покрытия всей поверхности Земли.

Обогащенный круг

Просмотрено с использованием исчисление, функция перехода круга Т это просто функция между открытыми интервалами, которая придает смысл утверждению, что Т является дифференцируемый. Карта перехода Т, и все остальные дифференцируемы на (0, 1); следовательно, в этом атласе круг является дифференцируемое многообразие. Это также гладкий; плавный и аналитический потому что функции перехода также обладают этими свойствами.

Другие свойства круга позволяют удовлетворить требования более специализированных типов коллекторов. Например, окружность означает расстояние между двумя точками, длину дуги между точками; следовательно, это Риманово многообразие.

Другие кривые

Четыре коллектора из алгебраические кривые: ■ круги ■ парабола ■ гипербола ■ кубический.

Коллекторы не обязательно связаны (все в «одном куске»); пример - пара отдельных кругов.

Коллекторы не обязательно закрыто; таким образом, отрезок без его концов является многообразием. И они никогда не счетный, если размер многообразия не равен 0. Объединяя эти свободы, другие примеры многообразий - парабола, а гипербола (две открытых, бесконечных части), и локус точек на кубическая кривая у² = Икс³ − Икс (деталь с замкнутым контуром и открытая, бесконечная деталь).

Однако исключены такие примеры, как два соприкасающихся круга, которые имеют общую точку, образуя восьмерку; в общей точке нельзя создать удовлетворительную диаграмму. Даже с учетом изгиба, допускаемого топологией, близость общей точки выглядит как «+», а не как линия. Знак «+» не гомеоморфен замкнутому интервалу (отрезку линии), поскольку удаление центральной точки из «+» дает пространство с четырьмя составные части (т.е. кусочки), тогда как удаление точки из закрытого интервала дает пространство максимум с двумя частями; топологические операции всегда сохраняйте количество штук.

Математическое определение

Неформально многообразие - это Космос это "смоделировано" Евклидово пространство.

В зависимости от контекста существует множество различных типов многообразий. В геометрия и топология, все многообразия топологические многообразия, возможно, с дополнительной структурой, такой как дифференцируемая структура. Многообразие может быть построено путем задания набора координатных карт, то есть покрытия открытыми множествами с гомеоморфизмами евклидова пространства, и функций вставки: гомеоморфизмов из одной области евклидова пространства в другую область, если они соответствуют одной и той же части пространства. многообразие в двух разных координатных картах. Многообразию можно придать дополнительную структуру, если функции склеивания удовлетворяют аксиомам за пределами непрерывности. Например, дифференцируемые многообразия имеют гомеоморфизмы на перекрывающихся окрестностях диффеоморфный друг с другом, так что многообразие имеет четко определенный набор функций, дифференцируемых в каждой окрестности и, следовательно, дифференцируемых на многообразии в целом.

Формально (топологическое) многообразие - это второй счетный Пространство Хаусдорфа который локально гомеоморфен евклидову пространству.

Второй счетный и Хаусдорф находятся набор точек условия; второй счетный исключает пробелы, которые в некотором смысле "слишком большие", такие как длинная линия, в то время как Хаусдорф исключает такие пространства, как «прямая с двумя началами» (эти обобщения многообразий обсуждаются в нехаусдорфовы многообразия ).

Локально гомеоморфный в евклидово пространство означает, что каждая точка имеет окрестность гомеоморфный к открытому Евклидово п-мяч,

{ displaystyle mathbf {B} ^ {n} = left {(x_ {1}, x_ {2}, dots, x_ {n}) in mathbb {R} ^ {n} mid x_ {1} ^ {2} + x_ {2} ^ {2} + cdots + x_ {n} ^ {2} <1 right }.}

Точнее, локально гомеоморфный здесь означает, что каждая точка м в коллекторе M имеет открытую окрестность, гомеоморфную открытой район в евклидовом пространстве, а не конкретно на единичный шар. Однако при таком гомеоморфизме прообраз ${ displaystyle epsilon}$ -бол дает гомеоморфизм между единичным шаром и меньшей окрестностью м, так что это не потеря общности. Для топологических или дифференцируемых многообразий можно также попросить, чтобы каждая точка имела окрестность, гомеоморфную всему евклидову пространству (поскольку она диффеоморфна единичному шару), но этого нельзя сделать для комплексные многообразия, поскольку сложный единичный шар не голоморфный в сложное пространство.

Обычно считается, что многообразия имеют фиксированную размерность (пространство должно быть локально гомеоморфно фиксированному п-шар), и такое пространство называется п-многообразие; однако некоторые авторы допускают многообразия, в которых разные точки могут иметь разные размеры.^[1] Если многообразие имеет фиксированный размер, его называют чистый коллектор. Например, сфера (поверхность) имеет постоянный размер 2 и, следовательно, является чистым многообразием, тогда как несвязный союз сферы и линии в трехмерном пространстве есть нет чистое многообразие. Поскольку измерение является локальным инвариантом (т. Е. Карта, отправляющая каждую точку в измерение ее окрестности, по которой определяется диаграмма, является локально постоянный ), каждый связный компонент имеет фиксированный размер.

Схематически-теоретически, многообразие - это локально окольцованное пространство, структурный пучок которого локально изоморфен пучку непрерывных (или дифференцируемых, или комплексно-аналитических и т. д.) функций на евклидовом пространстве. Это определение чаще всего используется при обсуждении аналитические многообразия в алгебраическая геометрия.

Диаграммы, атласы и карты переходов

Для навигации по сферической Земле используются плоские карты или диаграммы, собранные в атлас. Аналогично дифференцируемое многообразие можно описать с помощью математические карты, называется карты координат, собранные в математическом атлас. Обычно невозможно описать многообразие с помощью только одной карты, потому что глобальная структура многообразия отличается от простой структуры карт. Например, ни одна плоская карта не может представить всю Землю без разделения смежных объектов по границам карты или дублирования покрытия. Когда коллектор строится из нескольких перекрывающихся диаграмм, области, в которых они перекрываются, несут информацию, необходимую для понимания глобальной структуры.

Диаграммы

А карта координат, а карта координат, или просто диаграмма, многообразия является обратимым карта между подмножеством многообразия и простым пространством, такое что как отображение, так и его обратное сохраняют желаемую структуру.^[2] Для топологического многообразия простое пространство является подмножеством некоторого Евклидово пространство р^п и интерес сосредоточен на топологической структуре. Эта структура сохраняется гомеоморфизмы, обратимые отображения, непрерывные в обоих направлениях.

В случае дифференцируемое многообразие, набор графики называется атлас позволяет нам проводить вычисления на многообразиях. Полярные координаты, например, сформировать карту самолета р² минус положительный Икс-ось и начало координат. Другой пример карты - это отображение χ_верх упомянутый в разделе выше, диаграмма для круга.

Атласы

Для описания большинства многообразий требуется более одной карты (одна карта подходит только для простейших многообразий). Конкретный набор карт, покрывающий многообразие, называется атлас. Атлас не уникален, поскольку все многообразия можно охватить разными способами, используя различные комбинации диаграмм. Два атласа называются эквивалентными, если их объединение также является атласом.

Атлас, содержащий все возможные схемы, согласующиеся с данным атласом, называется максимальный атлас (т.е.класс эквивалентности, содержащий данный атлас (в соответствии с уже определенным отношением эквивалентности, приведенным в предыдущем абзаце)). В отличие от обычного атласа, максимальный атлас данного многообразия единственен. Хотя это полезно для определений, это абстрактный объект, который не используется напрямую (например, в расчетах).

Карты переходов

Графики в атласе могут перекрываться, и одна точка коллектора может быть представлена на нескольких картах. Если две карты накладываются друг на друга, части из них представляют одну и ту же область многообразия, точно так же, как карта Европы и карта Азии могут содержать Москву. Учитывая две пересекающиеся диаграммы, функция перехода можно определить, который идет от открытого шара в р^п в многообразие, а затем обратно в другой (или, возможно, тот же) открытый шар в р^п. Результирующая карта, как и карта Т в приведенном выше примере круга называется изменение координат, а преобразование координат, а функция перехода, или карта перехода.

Дополнительная конструкция

Атлас также можно использовать для определения дополнительной структуры коллектора. Структура сначала определяется на каждой диаграмме отдельно. Если все карты переходов совместимы с этой структурой, структура переходит на многообразие.

Это стандартный способ определения дифференцируемых многообразий. Если переходные функции атласа топологического многообразия сохраняют естественную дифференциальную структуру р^п (то есть, если они диффеоморфизмы ) дифференциальная структура переходит на многообразие и превращает его в дифференцируемое многообразие. Комплексные многообразия вводятся аналогичным образом, требуя, чтобы функции перехода атласа были голоморфные функции. За симплектические многообразия, функции перехода должны быть симплектоморфизмы.

Структура многообразия зависит от атласа, но иногда можно сказать, что разные атласы порождают одну и ту же структуру. Такие атласы называются совместимый.

Эти понятия в целом уточняются за счет использования псевдогруппы.

Многообразие с краем

А многообразие с краем - многообразие с ребром. Например, лист бумаги - это 2-х коллекторный с одномерной границей. Граница п-многообразие с краем является (п−1)-многообразие. А диск (круг плюс внутренность) - двумерное многообразие с краем. Его граница - круг, 1-коллектор. А квадрат с внутренностью также является двумерным многообразием с краем. А мяч (сфера плюс внутренность) - трехмерное многообразие с краем. Его край - сфера, двумерное многообразие. (Смотрите также Граница (топология) ).

Говоря техническим языком, многообразие с краем - это пространство, содержащее как внутренние, так и граничные точки. Каждая внутренняя точка имеет окрестность, гомеоморфную открытой п-мяч {(Икс₁, Икс₂, …, Икс_п) | ΣИкс_я² < 1}. Каждая граничная точка имеет окрестность, гомеоморфную «половине». п-мяч {(Икс₁, Икс₂, …, Икс_п) | ΣИкс_я² <1 и Икс₁ ≥ 0} . Гомеоморфизм должен переводить каждую граничную точку в точку с Икс₁ = 0.

Граница и интерьер

Позволять M - многообразие с краем. В интерьер из M, обозначается Int M, - множество точек в M окрестности которых гомеоморфны открытому подмножеству р^п. В граница из M, обозначается ∂M, это дополнять из Int M в M. Граничные точки можно охарактеризовать как точки, которые попадают на граничную гиперплоскость. (Икс_п = 0) из р^п₊ под какой-то координатной картой.

Если M многообразие с границей размерности п, затем Int M является многообразием (без края) размерности п и ∂M является многообразием (без края) размерности п − 1.

Строительство

Одиночный коллектор может быть сконструирован по-разному, каждый из которых подчеркивает разные аспекты коллектора, что приводит к несколько иной точке зрения.

Диаграммы

График отображает часть сферы с положительным z координаты к диску.

Возможно, самый простой способ построить многообразие - это тот, который использовался в приведенном выше примере круга. Во-первых, подмножество р² идентифицируется, а затем строится атлас, охватывающий это подмножество. Концепция чего-либо многообразие исторически вырос из таких построек. Вот еще один пример применения этого метода к построению сферы:

Сфера с графиками

А сфера можно рассматривать почти так же, как круг. В математике сфера - это просто поверхность (не внутренняя часть тела), которую можно определить как подмножество р³:

{ Displaystyle S = left {(x, y, z) in mathbf {R} ^ {3} mid x ^ {2} + y ^ {2} + z ^ {2} = 1 right }.}

Сфера двумерна, поэтому каждая диаграмма отображает часть сферы в открытое подмножество р². Рассмотрим северное полушарие, которое является частью положительного z координата (окрашена в красный цвет на картинке справа). Функция χ, определяемая формулой

{ Displaystyle чи (х, у, г) = (х, у), }

отображает северное полушарие на открытую единичный диск проецируя его на (Икс, у) самолет. Аналогичная диаграмма существует для южного полушария. Вместе с двумя графиками, проецируемыми на (Икс, z) и две карты, проецируемые на (у, z) плоскости получается атлас из шести карт, охватывающий всю сферу.

Это можно легко обобщить на сферы более высоких измерений.

Пэчворк

Многообразие можно построить, склеивая части последовательно, превращая их в перекрывающиеся диаграммы. Эта конструкция возможна для любого многообразия и поэтому часто используется как характеристика, особенно для дифференцируемых и римановых многообразий. Основное внимание в нем уделяется атласу, поскольку патчи, естественно, представляют собой диаграммы, а поскольку внешнее пространство не задействовано, это приводит к внутреннему представлению о многообразии.

Многообразие строится путем указания атласа, который сам определяется картами переходов. Следовательно, точка многообразия - это класс эквивалентности точек, которые сопоставлены друг с другом картами переходов. Графики сопоставляют классы эквивалентности с точками одного патча. Обычно предъявляются строгие требования к согласованности карт перехода. Для топологических многообразий они должны быть гомеоморфизмы; если они также диффеоморфизмы, получившееся многообразие является дифференцируемым многообразием.

Это можно проиллюстрировать картой перехода т = ¹⁄_s из второй половины круга примера. Начните с двух копий линии. Используйте координату s для первого экземпляра, и т для второго экземпляра. Теперь склейте обе копии вместе, указав точку т на втором экземпляре с точкой s = ¹⁄_т на первом экземпляре (точки т = 0 и s = 0 не отождествляются ни с одной точкой на первой и второй копии соответственно). Это дает круг.

Внутренний и внешний вид

Первая конструкция и эта конструкция очень похожи, но представляют собой довольно разные точки зрения. В первой конструкции многообразие выглядит как встроенный в некотором евклидовом пространстве. Это внешний вид. Когда многообразие рассматривается таким образом, легко использовать интуицию из евклидовых пространств для определения дополнительной структуры. Например, в евклидовом пространстве всегда ясно, является ли вектор в некоторой точке тангенциальный или же нормальный на некую поверхность через эту точку.

Конструкция пэчворк не использует вложения, а просто рассматривает многообразие как топологическое пространство само по себе. Эта абстрактная точка зрения называется внутренний взгляд. Это может затруднить представление о том, что может быть касательным вектором, и нет внутреннего понятия нормального пучка, но вместо этого существует внутреннее стабильный нормальный пакет.

п-Сфера как лоскутное одеяло

В п-сфера S^п является обобщением идеи круга (1-сфера) и сферы (2-сфера) на более высокие измерения. An п-сфера S^п можно построить, склеив две копии р^п. Карта перехода между ними определяется как

{ Displaystyle mathbf {R} ^ {n} setminus {0 } to mathbf {R} ^ {n} setminus {0 }: x mapsto x / | x | ^ { 2}.}

Эта функция является собственной инверсией и поэтому может использоваться в обоих направлениях. Поскольку карта перехода - это гладкая функция, этот атлас определяет гладкое многообразие. п = 1, пример упрощается до примера с кругом, приведенного ранее.

Определение точек многообразия

Можно сделать разные точки многообразия одинаковыми. Это можно представить как соединение этих точек в одну точку, образуя факторное пространство. Однако нет оснований ожидать, что такие фактор-пространства будут многообразиями. Среди возможных фактор-пространств, которые не обязательно являются многообразиями, орбифолды и Комплексы CW считаются относительно хорошо воспитанный. Примером фактор-пространства многообразия, которое также является многообразием, является реальное проективное пространство идентифицируется как фактор-пространство соответствующей сферы.

Один из методов идентификации точек (склеивания их) - это правое (или левое) действие группа, который действует на коллекторе. Две точки идентифицируются, если одна перемещается на другую каким-либо элементом группы. Если M это многообразие и грамм группа, полученное фактор-пространство обозначается через M / грамм (или же грамм \ M).

Коллекторы, которые могут быть построены путем определения точек, включают: тори и реальные проективные пространства (начиная с плоскости и шара соответственно).

Склейка по границам

Два многообразия с краями можно склеить по границе. Если все сделать правильно, результат тоже будет многообразием. Точно так же можно склеить две границы одного многообразия.

Формально склейка определяется биекция между двумя границами^{[сомнительный – обсуждать]}. Две точки идентифицируются, когда они накладываются друг на друга. Для топологического многообразия эта биекция должна быть гомеоморфизмом, иначе результат не будет топологическим многообразием. Аналогично, для дифференцируемого многообразия оно должно быть диффеоморфизм. Для других коллекторов следует сохранить другие конструкции.

Конечный цилиндр можно построить как многообразие, начав с полосы [0, 1] × [0, 1] и склеив пару противоположных ребер на границе подходящим диффеоморфизмом. А проективная плоскость может быть получен приклеиванием шара с отверстием в Лента Мебиуса вдоль их соответствующих круговых границ.

Декартовы произведения

В Декартово произведение многообразий также является многообразием.

Размер коллектора продукта - это сумма размеров его факторов. Его топология - это топология продукта, а декартово произведение диаграмм - это диаграмма для многообразия произведений. Таким образом, атлас многообразия произведений может быть построен с использованием атласов его факторов. Если эти атласы определяют дифференциальную структуру на факторах, соответствующий атлас определяет дифференциальную структуру на многообразии продукта. То же верно и для любой другой структуры, определенной на факторах. Если у одного из факторов есть граница, то и у производного многообразия есть граница. Декартовы произведения могут использоваться для построения торов и конечных цилиндры, например, как S¹ × S¹ и S¹ × [0, 1] соответственно.

Конечный цилиндр - это многообразие с краем.

История

Изучение многообразий объединяет многие важные области математики: оно обобщает такие понятия, как кривые и поверхности, а также идеи из линейная алгебра и топология.

Ранняя разработка

До появления современной концепции многообразия было несколько важных результатов.

Неевклидова геометрия рассматривает места, где Евклид с параллельный постулат терпит неудачу. Саккери впервые изучил такую геометрию в 1733 году, но стремился только опровергнуть их. Гаусс, Бойяи и Лобачевский независимо открыл их 100 лет спустя. Их исследование выявило два типа пространств, геометрическая структура которых отличается от классических. Евклидово пространство; это привело к гиперболическая геометрия и эллиптическая геометрия. В современной теории многообразий этим понятиям соответствуют Римановы многообразия с постоянным отрицательным и положительным кривизна, соответственно.

Карл Фридрих Гаусс возможно, был первым, кто рассматривал абстрактные пространства как самостоятельные математические объекты. Его теорема эгрегиум дает метод вычисления кривизна из поверхность без учета окружающее пространство в котором лежит поверхность. Такую поверхность в современной терминологии можно было бы назвать многообразием; и, говоря современным языком, теорема доказала, что кривизна поверхности внутренняя собственность. Теория многообразий фокусируется исключительно на этих внутренних свойствах (или инвариантах), в значительной степени игнорируя внешние свойства окружающего пространства.

Другой, более топологический пример внутреннего свойство многообразия является его Эйлерова характеристика. Леонард Эйлер показал, что для выпуклой многогранник в трехмерном евклидовом пространстве с V вершины (или углы), E края и F лица

{ Displaystyle V-E + F = 2. }

Та же формула верна, если спроецировать вершины и ребра многогранника на сфера, создавая топологическая карта с V вершины, E края и F грани, и на самом деле, останется верным для любого сферического отображения, даже если оно не возникает из какого-либо выпуклого многогранника.^[3] Таким образом, 2 - это топологический инвариант сферы, называемый ее Эйлерова характеристика. С другой стороны, тор могут быть разрезаны его «параллельными» и «меридиональными» кругами, создавая карту с V = 1 вершина, E = 2 ребра и F = 1 лицо. Таким образом, эйлерова характеристика тора равна 1-2 + 1 = 0. Эйлерова характеристика других поверхностей является полезным топологический инвариант, который можно расширить до более высоких измерений, используя Бетти числа. В середине девятнадцатого века Теорема Гаусса – Бонне связал эйлерову характеристику с гауссовой кривизной.

Синтез

Исследования Нильс Хенрик Абель и Карл Густав Якоби об инверсии эллиптические интегралы в первой половине XIX века заставили их рассматривать особые виды комплексные многообразия, теперь известный как Якобианцы. Бернхард Риманн внесла свой вклад в их теорию, прояснив геометрический смысл процесса аналитическое продолжение функций комплексных переменных.

Еще одним важным источником многообразий в математике XIX века был аналитическая механика, разработанная Симеон Пуассон, Якоби и Уильям Роуэн Гамильтон. Возможные состояния механической системы считаются точками абстрактного пространства, фазовое пространство в Лагранжиан и Гамильтониан формализмы классической механики. Фактически это пространство представляет собой многомерное многообразие, измерение соответствует степеням свободы системы, а точки задаются своими обобщенные координаты. Для неограниченного движения свободных частиц многообразие эквивалентно евклидову пространству, но с различными законы сохранения ограничить его более сложными формациями, например Лиувилля торы. Теория вращающегося твердого тела, разработанная в 18 веке А. Леонард Эйлер и Жозеф-Луи Лагранж, дает еще один пример, когда многообразие нетривиально. Геометрические и топологические аспекты классической механики подчеркивали Анри Пуанкаре, один из основателей топология.

Риман был первым, кто проделал обширную работу по обобщению идеи поверхности на более высокие измерения. Название многообразие происходит от оригинала Римана Немецкий срок, Mannigfaltigkeit, который Уильям Кингдон Клиффорд переводится как «многообразие». В своей вступительной лекции в Геттингене Риман описал множество всех возможных значений переменной с определенными ограничениями как Mannigfaltigkeit, потому что переменная может иметь много значения. Он различает stetige Mannigfaltigkeit и дискрет Mannigfaltigkeit (непрерывное многообразие и разрывное многообразие), в зависимости от того, изменяется ли значение постоянно или нет. В качестве непрерывных примеров Риман обращается не только к цветам и расположению предметов в пространстве, но и к возможным формам пространственной фигуры. С помощью индукция, Риман строит n-fach ausgedehnte Mannigfaltigkeit (n раз расширенное многообразие или же n-мерное многообразие) как непрерывный стек (n - 1) мерных многообразий. Интуитивное представление Римана о Mannigfaltigkeit превратились в то, что сегодня формализовано как многообразие. Римановы многообразия и Римановы поверхности названы в честь Римана.

Определение Пуанкаре

В своей очень влиятельной статье Analysis Situs,^[4] Анри Пуанкаре дал определение (дифференцируемого) многообразия (вариет), который послужил предшественником современной концепции многообразия.^[5]

В первом разделе Analysis Situs Пуанкаре определяет многообразие как набор уровня непрерывно дифференцируемый функция между евклидовыми пространствами, удовлетворяющая гипотезе невырожденности теорема о неявной функции. В третьем разделе он начинает с того, что отмечает, что график непрерывно дифференцируемой функции является многообразием в последнем смысле. Затем он предлагает новое, более общее определение многообразия, основанное на «цепочке многообразий» (une chaîne des varétés).

Понятие Пуанкаре о цепочка многообразий является предшественником современного представления о атлас. В частности, он рассматривает два многообразия, определяемых соответственно как графики функций ${ displaystyle theta (y)}$ и ${ Displaystyle тета ' влево (у' вправо)}$ . Если эти многообразия перекрываются (Коммуна un partie), то он требует, чтобы координаты ${ displaystyle y}$ непрерывно дифференцируемо зависят от координат ${ displaystyle y '}$ наоборот ('... les ${ displaystyle y}$ sont fonctions analytiques des ${ displaystyle y '}$ и обратное'). Таким образом, он вводит предшественник понятия диаграмма и из карта перехода. В Analysis Situs неявно подразумевается, что многообразие, полученное как «цепь», является подмножеством евклидова пространства.

Например, единичный круг на плоскости можно рассматривать как график функции ${ displaystyle y = { sqrt {1-x ^ {2}}}}$ иначе функция ${ displaystyle y = - { sqrt {1-x ^ {2}}}}$ в окрестности каждой точки, кроме точек (1, 0) и (−1, 0); и в окрестности этих точек его можно рассматривать как график соответственно ${ Displaystyle х = { sqrt {1-y ^ {2}}}}$ и ${ displaystyle x = - { sqrt {1-y ^ {2}}}}$ . Причина, по которой круг может быть представлен графом в окрестности каждой точки, заключается в том, что левая часть его определяющего уравнения ${ displaystyle x ^ {2} + y ^ {2} -1 = 0}$ имеет ненулевой градиент в каждой точке круга. Посредством теорема о неявной функции, каждый подмногообразие евклидова пространства локально является графиком функции.

Герман Вейль дал внутреннее определение дифференцируемых многообразий в своем курсе лекций о римановых поверхностях в 1911–1912 гг., открыв путь к общей концепции топологическое пространство это последовало вскоре. В 1930-е гг. Хасслер Уитни и другие разъяснили основополагающий аспекты предмета, и, таким образом, интуиция, относящаяся ко второй половине 19 века, стала точной и развивалась через дифференциальная геометрия и Группа Ли теория. Примечательно, что Теорема вложения Уитни^[6] показал, что внутреннее определение в терминах карт эквивалентно определению Пуанкаре в терминах подмножеств евклидова пространства.

Топология многообразий: основные моменты

Двумерные многообразия, также известные как 2D поверхности встроенные в наше общее трехмерное пространство, Риман рассматривал под видом Римановы поверхности, и строго классифицированный в начале 20 века Пол Хегаард и Макс Ден. Анри Пуанкаре был пионером в изучении трехмерных многообразий и поднял о них фундаментальный вопрос, сегодня известный как Гипотеза Пуанкаре. Спустя почти столетие усилий многих математиков, начиная с самого Пуанкаре, Григорий Перельман доказал гипотезу Пуанкаре (см. Решение гипотезы Пуанкаре ). Уильям Терстон с программа геометризации, сформулированная в 1970-х годах, обеспечила далеко идущее распространение гипотезы Пуанкаре на общие трехмерные многообразия. Четырехмерные многообразия были выдвинуты на передний план математических исследований в 1980-х годах благодаря Майкл Фридман и в другой обстановке Саймон Дональдсон, который был мотивирован недавним прогрессом теоретической физики (Теория Янга – Миллса ), где они служат заменой обычным «плоским» пространство-время. Андрей Марков мл. в 1960 году показал, что не существует алгоритма классификации четырехмерных многообразий. Важная работа над многомерными многообразиями, включая аналоги гипотезы Пуанкаре, было сделано ранее Рене Том, Джон Милнор, Стивен Смейл и Сергей Новиков. Один из наиболее распространенных и гибких методов, лежащих в основе многих работ топология многообразий является Теория Морса.

Дополнительная конструкция

Топологические многообразия

Самый простой вид многообразия для определения - это топологическое многообразие, которое локально выглядит как какое-то "обычное" Евклидово пространство р^п. По определению, все многообразия являются топологическими многообразиями, поэтому фраза «топологическое многообразие» обычно используется, чтобы подчеркнуть, что у многообразия отсутствует дополнительная структура или что рассматриваются только его топологические свойства. Формально топологическое многообразие - это топологическое пространство локально гомеоморфный в евклидово пространство. Это означает, что каждая точка имеет окрестность, для которой существует гомеоморфизм (а биективный непрерывная функция обратный к которому также непрерывен), отображая эту окрестность в р^п. Эти гомеоморфизмы являются картами многообразия.

А топологический многообразие выглядит локально как евклидово пространство довольно слабо: в то время как для каждой отдельной карты можно различать дифференцируемые функции или измерять расстояния и углы, просто в силу того, что пространство является топологическим многообразием, пространство не имеет никаких частности и последовательный выбор таких понятий. Чтобы обсудить такие свойства для многообразия, необходимо определить дальнейшую структуру и рассмотреть дифференцируемые многообразия и Римановы многообразия обсуждается ниже. В частности, одно и то же лежащее в основе топологическое многообразие может иметь несколько несовместимых классов дифференцируемых функций и бесконечное количество способов задания расстояний и углов.

Обычно для исключения патологических случаев делаются дополнительные технические предположения о топологическом пространстве. Принято требовать, чтобы пространство было Хаусдорф и второй счетный.

В измерение многообразия в определенной точке - это размер евклидова пространства, в которое карты в этой точке отображают (число п в определении). Все точки в связаны коллектор имеют такой же размер. Некоторые авторы требуют, чтобы все карты топологического многообразия отображались в евклидовы пространства той же размерности. В этом случае каждое топологическое многообразие имеет топологический инвариант - свою размерность. Другие авторы разрешают называть несвязные объединения топологических многообразий разных размерностей многообразиями.

Дифференцируемые многообразия

Для большинства приложений особый вид топологического многообразия, а именно дифференцируемое многообразие, используется. Если локальные карты на многообразии совместимы в определенном смысле, можно определить направления, касательные пространства и дифференцируемые функции на этом многообразии. В частности, можно использовать исчисление на дифференцируемом многообразии. Каждая точка п-мерное дифференцируемое многообразие имеет касательное пространство. Это п-мерное евклидово пространство, состоящее из касательные векторы кривых через точку.

Два важных класса дифференцируемых многообразий: гладкий; плавный и аналитические многообразия. Для гладких многообразий карты переходов имеют вид гладкий; плавный, которая бесконечно дифференцируема. Аналитические многообразия - это гладкие многообразия с дополнительным условием, что отображения переходов аналитический (их можно выразить как степенной ряд ). Сфере можно придать аналитическую структуру, как и большинству знакомых кривых и поверхностей.

Существуют также топологические многообразия, т. Е. Локально евклидовы пространства, которые вообще не имеют дифференцируемых структур.^[7]

А выпрямляемый набор обобщает идею кусочно-гладкой или выпрямляемая кривая в более высокие измерения; однако спрямляемые множества не являются общими многообразиями.

Римановы многообразия

Для измерения расстояний и углов на многообразиях многообразие должно быть римановым. А Риманово многообразие является дифференцируемым многообразием, в котором каждое касательное пространство оснащен внутренний продукт $⟨\cdot , \cdot⟩$ способом, который плавно меняется от точки к точке. Учитывая два касательных вектора $ты$ и $v$ , внутренний продукт $⟨ ты, v ⟩$ дает реальное число. В точка (или скалярное) произведение - типичный пример внутреннего продукта. Это позволяет определять различные понятия, такие как длина, углы, области (или же тома ), кривизна и расхождение из векторные поля.

Всем дифференцируемым многообразиям (постоянной размерности) можно придать структуру риманова многообразия. Само евклидово пространство несет естественную структуру риманова многообразия (касательные пространства естественно отождествляются с самим евклидовым пространством и несут стандартное скалярное произведение пространства). Многие знакомые кривые и поверхности, включая, например, все $п$ -сферы, задаются как подпространства евклидова пространства и наследуют метрику от своего вложения в него.

Финслеровы многообразия

А Финслеровский коллектор позволяет определять расстояние, но не требует понятия угла; это аналитическое многообразие, в котором каждое касательное пространство оснащен норма, || · ||, плавно изменяющимся от точки к точке. Эту норму можно расширить до метрика, определяя длину кривой; но, как правило, его нельзя использовать для определения внутреннего продукта.

Любое риманово многообразие является финслеровым многообразием.

Группы Ли

Группы Ли, названный в честь Софус Ли, являются дифференцируемыми многообразиями, несущими также структуру группа что такое, что групповые операции задаются гладкими отображениями.

Евклидово векторное пространство с групповой операцией сложения векторов является примером некомпактной группы Ли. Простой пример компактный Группа Ли - это круг: групповая операция - это просто вращение. Эту группу, известную как U (1), также можно охарактеризовать как группу сложные числа из модуль 1 с умножением как групповой операцией.

Другие примеры групп Ли включают специальные группы матрицы, которые являются подгруппами группы общая линейная группа, группа п к п матрицы с ненулевым определителем. Если элементы матрицы действительные числа, это будет п²-мерное несвязное многообразие. В ортогональные группы, то группы симметрии из сфера и гиперсферы, находятся п(п−1) / 2-мерных многообразий, где п−1 - размерность сферы. Дополнительные примеры можно найти в таблица групп Ли.

Другие типы коллекторов

А комплексное многообразие является многообразием, карты которого принимают значения в ${ displaystyle mathbb {C} ^ {n}}$ и чьи переходные функции голоморфный по перекрытиям. Эти многообразия являются основными объектами изучения в сложная геометрия. Одномерное комплексно-мерное многообразие называется Риманова поверхность. An п-мерное комплексное многообразие имеет размерность 2п как реальное дифференцируемое многообразие.
А CR-коллектор является многообразием, моделируемым на границах областей в ${ displaystyle mathbb {C} ^ {n}}$ .
«Бесконечномерные многообразия»: чтобы учесть бесконечные измерения, можно рассмотреть Банаховы многообразия которые локально гомеоморфны Банаховы пространства. Аналогично многообразия Фреше локально гомеоморфны Пространства фреше.
А симплектическое многообразие это разновидность многообразия, которое используется для представления фазовых пространств в классическая механика. Они наделены 2-форма что определяет Скобка Пуассона. Близким типом многообразий является контактный коллектор.
А комбинаторное многообразие является разновидностью многообразия, которое является дискретизацией многообразия. Обычно это означает кусочно-линейное многообразие сделан симплициальные комплексы.
А цифровой коллектор это особый вид комбинаторного многообразия, которое определяется в цифровом пространстве. Видеть цифровая топология

Классификация и инварианты

Разные понятия многообразий имеют разные понятия классификации и инварианта; в этом разделе мы сосредоточимся на гладких замкнутых многообразиях.

Классификация гладких замкнутых многообразий хорошо изучена. в общем, кроме размер 4: в малых размерах (2 и 3) он геометрический, через теорема униформизации и решение гипотезы Пуанкаре, а в большой размерности (5 и выше) она алгебраическая, через теория хирургии. Это принципиальная классификация: общий вопрос о диффеоморфности двух гладких многообразий сводится к следующему. не вычислим в общем. Кроме того, конкретные вычисления остаются сложными, и остается много открытых вопросов.

Ориентируемые поверхности можно визуализировать, а классы их диффеоморфизмов перечислить по родам. Учитывая две ориентируемые поверхности, можно определить, являются ли они диффеоморфными, вычислив их соответствующие роды и сравнив: они диффеоморфны тогда и только тогда, когда роды равны, поэтому род образует полный набор инвариантов.

Это намного сложнее в высших измерениях: многомерные многообразия нельзя непосредственно визуализировать (хотя визуальная интуиция полезна для их понимания), нельзя перечислить их классы диффеоморфизма, и нельзя в целом определить, есть ли два разных описания многомерного многообразие относятся к одному и тому же объекту.

Однако можно определить, являются ли два многообразия разные если есть какая-то внутренняя характеристика, которая их отличает. Такие критерии обычно называют инварианты, потому что, хотя они могут быть определены в терминах некоторого представления (например, род в терминах триангуляции), они одинаковы относительно всех возможных описаний конкретного многообразия: они инвариантный под разными описаниями.

Наивно можно было надеяться разработать арсенал инвариантных критериев, которые окончательно классифицировали бы все многообразия с точностью до изоморфизма. К сожалению, известно, что для многообразий размерности 4 и выше программы не существует который может решить, диффеоморфны ли два многообразия.

Гладкие коллекторы имеют богатый набор инвариантов, приходящий из точечная топология, классический алгебраическая топология, и геометрическая топология. Наиболее известные инварианты, видимые для поверхностей: ориентируемость (нормальный инвариант, также обнаруживаемый гомология ) и род (гомологический инвариант).

Гладкие замкнутые многообразия не имеют локальных инвариантов (кроме размерности), хотя геометрические многообразия имеют локальные инварианты, в частности кривизна риманова многообразия и кручение коллектора, снабженного аффинная связь Это различие между локальными инвариантами и отсутствием локальных инвариантов является обычным способом различения геометрия и топология. Таким образом, все инварианты гладкого замкнутого многообразия глобальны.

Алгебраическая топология является источником ряда важных глобальных инвариантных свойств. Некоторые ключевые критерии включают односвязный свойство и ориентируемость (см. ниже). Действительно, несколько разделов математики, такие как гомология и гомотопия теория и теория характеристические классы были основаны для изучения инвариантных свойств многообразий.

Поверхности

Ориентируемость

В размерностях два и выше простым, но важным критерием инвариантности является вопрос о том, допускает ли многообразие значимую ориентацию. Рассмотрим топологическое многообразие с картами, отображаемыми в р^п. Учитывая заказная основа за р^п, диаграмма заставляет ее часть коллектора сама по себе приобретать чувство упорядоченности, которое в 3-х измерениях можно рассматривать как правостороннее или левостороннее. Перекрывающиеся диаграммы не обязательно должны согласовываться в смысле упорядочивания, что дает множествам важную свободу. Для некоторых многообразий, таких как сфера, диаграммы могут быть выбраны так, чтобы перекрывающиеся области согласовывали свою «ручность»; Эти ориентируемый коллекторы. Для других это невозможно. Последнюю возможность легко упустить, поскольку любая замкнутая поверхность, вложенная (без самопересечения) в трехмерное пространство, ориентируема.

Некоторые иллюстративные примеры неориентируемых многообразий включают: (1) Лента Мебиуса, которое является многообразием с краем, (2) Бутылка Клейна, который должен пересекаться в своем 3-пространственном представлении, и (3) реальная проективная плоскость, который естественно возникает в геометрия.

Лента Мебиуса

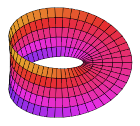
Начните с бесконечного кругового цилиндра, стоящего вертикально, многообразия без границ. Разрежьте его сверху и снизу, чтобы образовались две круглые границы и цилиндрическая полоса между ними. Это ориентируемое многообразие с краем, на котором будет проведена «операция». Разрежьте полоску так, чтобы она могла развернуться, чтобы получился прямоугольник, но держитесь за обрезанные концы. Поверните один конец на 180 °, чтобы внутренняя поверхность была обращена наружу, и склейте концы обратно без шва. В результате получается полоса с постоянным полувручением: Лента Мебиуса. Его граница больше не пара окружностей, а (топологически) одна окружность; и то, что когда-то было его "внутренним", слилось с его "внешностью", так что теперь у него есть только Один сторона. Подобно бутылке Клейна ниже, эта двумерная поверхность должна пересекаться в двух измерениях, но ее можно легко построить в трех или более измерениях.

Бутылка Клейна

Бутылка Кляйна в трехмерном пространстве

Возьмите две полоски Мебиуса; каждая имеет одну петлю в качестве границы. Распрямите эти петли в кружочки и позвольте полоскам деформироваться в кросс-кепки. Склеивание кругов вместе даст новое замкнутое многообразие без границ, Бутылка Клейна. Закрытие поверхности ничего не делает для улучшения отсутствия ориентируемости, оно просто удаляет границу. Таким образом, бутылка Клейна представляет собой закрытую поверхность без различия между внутренней и внешней стороной. В трехмерном пространстве поверхность бутылки Клейна должна проходить сквозь себя. Создание бутылки Клейна, которая не является самопересекающейся, требует четырех или более пространственных измерений.

Реальная проективная плоскость

Начните со сферы с центром в начале координат. Каждая линия, проходящая через начало координат, пронизывает сферу в двух противоположных точках, называемых антиподы. Хотя физически это сделать невозможно, это возможно (учитывая факторное пространство ), чтобы математически объединить каждую пару антиподов в одну точку. Изготовленная таким образом замкнутая поверхность является реальная проективная плоскость, еще одна неориентируемая поверхность. Он имеет ряд эквивалентных описаний и построений, но этот маршрут объясняет его название: все точки на любой заданной прямой через исходную точку проецируются в одну и ту же «точку» на этой «плоскости».

Род и эйлерова характеристика

Для двумерных многообразий ключевым инвариантным свойством является род, или «количество ручек» на поверхности. Тор - это сфера с одной ручкой, двойной тор - это сфера с двумя ручками и т. Д. Действительно, компактные двумерные многообразия можно полностью охарактеризовать на основе их рода и ориентируемости. В многомерных многообразиях род заменяется понятием Эйлерова характеристика, и в более общем плане Бетти числа и гомология и когомология.

Карты многообразий

А Поверхность Морина, погружение используется в выворот сферы

Так же, как существуют различные типы коллекторов, существуют различные типы карты многообразий. В дополнение к непрерывным функциям и гладкие функции как правило, есть карты со специальными свойствами. В геометрическая топология основным типом являются вложения, из которых теория узлов является центральным примером и обобщениями, такими как погружения, погружения, покрытия пространства, и разветвленные перекрытия. Основные результаты включают Теорема вложения Уитни и Теорема Уитни об погружении.

В римановой геометрии можно попросить отображения для сохранения римановой метрики, что приводит к понятиям изометрические вложения, изометрические погружения, и Римановы субмерсии; основной результат - это Теорема вложения Нэша.

Скалярные функции

Трехмерный цветной график сферические гармоники степени

{ displaystyle n = 5}

Основным примером отображений между многообразиями являются скалярнозначные функции на многообразии,

{ displaystyle f двоеточие M to mathbf {R}}

или же

{ displaystyle f двоеточие M to mathbf {C},}

иногда называют регулярные функции или же функционалы, по аналогии с алгебраической геометрией или линейной алгеброй. Они представляют интерес как сами по себе, так и для изучения лежащего в основе многообразия.

В геометрической топологии наиболее часто изучаются: Функции Морса, которые дают ручка разложения, а в математический анализ, часто изучают решение уравнения в частных производных, важным примером чего является гармонический анализ, где учится гармонические функции: ядро Оператор Лапласа. Это приводит к таким функциям, как сферические гармоники, и чтобы тепловое ядро методы изучения многообразий, такие как слышать форму барабана и некоторые доказательства Теорема Атьи – Зингера об индексе.

Обобщения многообразий

Бесконечномерные многообразия: Определение многообразия можно обобщить, отказавшись от требования конечномерности. Таким образом, бесконечномерное многообразие - это топологическое пространство, локально гомеоморфное пространству. топологическое векторное пространство над реалами. При этом опускаются аксиомы точечного набора, что позволяет использовать более высокие мощности и нехаусдорфовы многообразия; и он пропускает конечную размерность, позволяя такие структуры, как Гильбертовы многообразия по образцу Гильбертовы пространства, Банаховы многообразия по образцу Банаховы пространства, и Многообразия Фреше по образцу Пространства фреше. Обычно ослабляется то или иное условие: многообразия с аксиомами точек изучаются в общая топология, а бесконечномерные многообразия изучаются в функциональный анализ.
Орбифолды: An орбифолд является обобщением многообразия, допускающим определенные виды "особенности "в топологии. Грубо говоря, это пространство, которое локально выглядит как фактор некоторого простого пространства (например Евклидово пространство ) посредством действия различных конечные группы. Особенности соответствуют неподвижным точкам действий группы, и действия должны быть в определенном смысле совместимыми.
Алгебраические многообразия и схемы: Неособое число алгебраические многообразия над действительными или комплексными числами являются многообразиями. Один из них обобщает это, во-первых, допуская сингулярности, во-вторых, допуская различные поля, и, в-третьих, имитируя конструкцию склеивания многообразий: так же, как многообразие склеивается из открытых подмножеств евклидова пространства, алгебраическое многообразие склеивается из аффинных алгебраических многообразий, которые являются нулевыми множествами многочленов над алгебраически замкнутыми полями. Схемы также склеиваются из аффинных схем, являющихся обобщением алгебраических многообразий. Оба связаны с многообразиями, но построены алгебраически с использованием снопы вместо атласов.; Потому что особые точки, разнообразие вообще не является многообразием, хотя с лингвистической точки зрения французское вариет, Немецкий Mannigfaltigkeit и английский многообразие в основном синоним. По-французски алгебраическое многообразие называется UNE Varété Algébrique (ан алгебраическое многообразие), а гладкое многообразие называется UNE varété différentielle (а дифференциальное разнообразие).
Стратифицированное пространство: «Стратифицированное пространство» - это пространство, которое может быть разделено на части («страты»), причем каждый слой представляет собой многообразие, при этом слои соответствуют друг другу заданным образом (формально фильтрация замкнутыми подмножествами). Существуют различные технические определения, в частности, стратифицированное пространство Уитни (см. Условия Уитни ) для гладких многообразий и a топологически стратифицированное пространство для топологических многообразий. Основные примеры включают многообразие с краем (многообразие высшей размерности и граница коразмерности 1) и многообразия с углами (многообразие высшей размерности, граница коразмерности 1, углы коразмерности 2). Стратифицированные пространства Уитни - это широкий класс пространств, включающий алгебраические многообразия, аналитические многообразия, полуалгебраические множества, и субаналитические множества.
CW-комплексы: А CW комплекс представляет собой топологическое пространство, образованное склейкой дисков разной размерности. В общем, получившееся пространство сингулярно и, следовательно, не является многообразием. Однако они представляют центральный интерес в алгебраическая топология, особенно в теория гомотопии, так как их легко вычислить, а особенности не вызывают беспокойства.
Гомологические многообразия: А многообразие гомологий является пространством, которое ведет себя как многообразие с точки зрения теории гомологии. Это не все многообразия, но (в большой размерности) их можно проанализировать с помощью теория хирургии подобно многообразиям, и отказ от многообразия является локальным препятствием, как в теории хирургии.^[8]
Дифференциальные пространства: Позволять ${ displaystyle M}$ быть непустым множеством. Предположим, что некоторое семейство действительных функций на ${ displaystyle M}$ был выбран. Обозначим это ${ Displaystyle C substeq mathbb {R} ^ {M}}$ . Это алгебра относительно поточечного сложения и умножения. Позволять ${ displaystyle M}$ быть снабжен топологией, индуцированной ${ displaystyle C}$ . Предположим также, что выполняются следующие условия. Первый: для каждого ${ displaystyle H in C ^ { infty} left ( mathbb {R} ^ {i} right)}$ , куда ${ Displaystyle я в mathbb {N}}$ , и произвольные ${ displaystyle f_ {1}, dots, f_ {n} in C}$ , сочинение ${ displaystyle H circ left (f_ {1}, dots, f_ {n} right) in C}$ . Во-вторых: каждая функция, которая в каждой точке ${ displaystyle M}$ локально совпадает с некоторой функцией из ${ displaystyle C}$ , также принадлежит ${ displaystyle C}$ . Пара ${ Displaystyle (М, С)}$ для которого выполняются указанные выше условия, называется дифференциальным пространством Сикорского.^[9]

Смотрите также

Геодезический - Кратчайший путь на искривленной поверхности или римановом многообразии
Направленная статистика: статистика по многообразиям
Список коллекторов - Статья со списком Википедии
Хронология многообразий - Хронология математики
Математика общей теории относительности - Математические структуры и методы, используемые в общей теории относительности.

По размеру

3-х коллекторный - Пространство, которое локально выглядит как евклидово трехмерное пространство
4-х коллекторный - Коллектор размерности четыре
5-коллекторный - Коллектор размерности пять
Многообразия отображений

Примечания

^ Например. видеть Риаза, Рикардо (2008), Дифференциально-алгебраические системы: аналитические аспекты и схемотехнические приложения, World Scientific, стр. 110, ISBN 9789812791818; Ганнинг, Р. К. (1990), Введение в голоморфные функции нескольких переменных, Том 2, CRC Press, стр. 73, ISBN 9780534133092.
^ Шигеюки Морита; Теруко Нагасе; Кацуми Номидзу (2001). Геометрия дифференциальных форм. Книжный магазин Американского математического общества. п.12. ISBN 0-8218-1045-6.
^ Понятие карты можно формализовать как разложение клеток.
^ Пуанкаре, Х. (1895). «Анализ Situs». Journal de l'École Polytechnique. Сери 11 (на французском языке). Готье-Виллар.
^ Арнольд, В.И. (1998). "О преподавании математики" [Об обучении математике]. Успехи матем. Наук (на русском). 53 (319): 229–234. Дои:10,4213 / пог.м5.; перевод на русский математик. Обзоры 53 (1998), вып. 1, 229–236
^ Уитни, Х. (1936). «Дифференцируемые многообразия». Анналы математики. Вторая серия. 37 (3): 645–680. Дои:10.2307/1968482. JSTOR 1968482.
^ Кервэр, М. (1961). «Многообразие, не допускающее никакой дифференцируемой структуры». Комментарий. Математика. Helv. 35 (1): 1–14. Дои:10.1007 / BF02565940.
^ Bryant, J .; Ферри, S .; Mio, W .; Вайнбергер, С. (1996). «Топология гомологических многообразий». Анналы математики. Вторая серия. 143 (3): 435–467. arXiv:математика / 9304210. Дои:10.2307/2118532. JSTOR 2118532.
^ Сикорский, Р. (1967). «Абстрактная ковариантная производная». Математический коллоквиум. 18: 251–272. Дои:10.4064 / см-18-1-251-272.

внешняя ссылка

"Многообразие", Энциклопедия математики, EMS Press, 2001 [1994]
Dimensions-math.org (Фильм, объясняющий и визуализирующий многообразие до четвертого измерения.)
В многообразный атлас проект Институт математики Макса Планка в Бонне

[1] Например. видеть Риаза, Рикардо (2008), Дифференциально-алгебраические системы: аналитические аспекты и схемотехнические приложения, World Scientific, стр. 110, ISBN 9789812791818; Ганнинг, Р. К. (1990), Введение в голоморфные функции нескольких переменных, Том 2, CRC Press, стр. 73, ISBN 9780534133092.

[Morita-2] Шигеюки Морита; Теруко Нагасе; Кацуми Номидзу (2001). Геометрия дифференциальных форм. Книжный магазин Американского математического общества. п.12. ISBN 0-8218-1045-6.

[3] Понятие карты можно формализовать как разложение клеток.

[4] Пуанкаре, Х. (1895). «Анализ Situs». Journal de l'École Polytechnique. Сери 11 (на французском языке). Готье-Виллар.

[5] Арнольд, В.И. (1998). "О преподавании математики" [Об обучении математике]. Успехи матем. Наук (на русском). 53 (319): 229–234. Дои:10,4213 / пог.м5.; перевод на русский математик. Обзоры 53 (1998), вып. 1, 229–236

[6] Уитни, Х. (1936). «Дифференцируемые многообразия». Анналы математики. Вторая серия. 37 (3): 645–680. Дои:10.2307/1968482. JSTOR 1968482.

[7] Кервэр, М. (1961). «Многообразие, не допускающее никакой дифференцируемой структуры». Комментарий. Математика. Helv. 35 (1): 1–14. Дои:10.1007 / BF02565940.

[bfmw-8] Bryant, J .; Ферри, S .; Mio, W .; Вайнбергер, С. (1996). «Топология гомологических многообразий». Анналы математики. Вторая серия. 143 (3): 435–467. arXiv:математика / 9304210. Дои:10.2307/2118532. JSTOR 2118532.

[sacd-9] Сикорский, Р. (1967). «Абстрактная ковариантная производная». Математический коллоквиум. 18: 251–272. Дои:10.4064 / см-18-1-251-272.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Многообразие - Manifold

Мотивирующие примеры

Круг

Сфера

Обогащенный круг

Другие кривые

Математическое определение

Диаграммы, атласы и карты переходов

Диаграммы

Атласы

Карты переходов

Дополнительная конструкция

Многообразие с краем

Граница и интерьер

Строительство

Диаграммы

Сфера с графиками

Пэчворк

Внутренний и внешний вид

п-Сфера как лоскутное одеяло

Определение точек многообразия

Склейка по границам

Декартовы произведения

История

Ранняя разработка

Синтез

Определение Пуанкаре

Топология многообразий: основные моменты

Дополнительная конструкция

Топологические многообразия

Дифференцируемые многообразия

Римановы многообразия

Финслеровы многообразия

Группы Ли

Другие типы коллекторов

Классификация и инварианты

Поверхности

Ориентируемость

Лента Мебиуса

Бутылка Клейна

Реальная проективная плоскость

Род и эйлерова характеристика

Карты многообразий

Скалярные функции

Обобщения многообразий

Смотрите также

По размеру

Примечания

Рекомендации

внешняя ссылка