Теория Янга – Миллса - Yang–Mills theory

Нерешенная проблема в физике: Теория Янга – Миллса в не-пертурбативный режим: уравнения Янга – Миллса остаются нерешенными при шкалы энергии актуально для описания атомные ядра. Как теория Янга – Миллса дает начало физике ядра и ядерные составляющие ? (больше нерешенных задач по физике)

Квантовая теория поля
Диаграмма Фейнмана
История
Задний план Теория поля Электромагнетизм Слабая сила Сильная сила Квантовая механика Специальная теория относительности Общая теория относительности Калибровочная теория
Симметрии Симметрия в квантовой механике C-симметрия P-симметрия Т-симметрия Симметрия переноса пространства Симметрия перевода времени Симметрия вращения Симметрия Лоренца Симметрия Пуанкаре Калибровочная симметрия Явное нарушение симметрии Спонтанное нарушение симметрии Теория Янга – Миллса Нётер заряд Топологический заряд
инструменты Аномалия Переход Эффективная теория поля Ценность ожидания Призрачные поля Призраки Фаддеева – Попова Диаграмма Фейнмана Решеточная калибровочная теория Формула восстановления LSZ Функция разделения Пропагатор Квантование Регуляризация Перенормировка Состояние вакуума Теорема Вика Аксиомы Вайтмана Параметризация Фейнмана
Уравнения Уравнение Дирака Уравнение Клейна – Гордона Уравнения Прока Уравнение Уиллера – ДеВитта Уравнения Баргмана – Вигнера Уравнение Джооса – Вайнберга Уравнение Вейля
Стандартная модель Квантовое вакуумное состояние Квантовая динамика Квантовая термодинамика Квантовая электродинамика Электрослабое взаимодействие Квантовая хромодинамика Механизм Хиггса Виртуальная частица
Неполные теории Причинная динамическая триангуляция Причинные фермионные системы Причинные множества Конформная теория поля Море Дирака Теория возмущений Двумерная конформная теория поля Квантовая теория поля в искривленном пространстве-времени Теория теплового квантового поля Топологическая квантовая теория поля Квантовая геометрия Полуклассическая гравитация Отжим пена Теория струн Теория суперструн М-Теория Суперсимметрия Супергравитация Разноцветный Теория всего Каноническая квантовая гравитация Квантовая гравитация Петлевая квантовая гравитация Петлевая квантовая космология Теория скрытых переменных Теория объективного коллапса
Ученые Адлер Андерсон Быть Боголюбов Коулман Каллан ДеВитт Дирак Дайсон Ферми Фейнман Фирц Фок Fröhlich Гелл-Манн Голдстоун Валовой Гейзенберг 'т Хофт Джеки Иордания Ландо Ли Lehmann Мандельштам Майорана Намбу Паризи Поляков Салам Швингер Skyrme Штюкельберг Симанзик Томонага Вельтман Вайнберг Weisskopf Weyl Вильчек Уилсон Виттен Ян Юкава Циммерманн Зинн-Джастин

Теория Янга – Миллса это калибровочная теория на основе особая унитарная группа SU (N ), или вообще любой компактный, редуктивная алгебра Ли. Теория Янга – Миллса пытается описать поведение элементарных частиц, используя эти неабелев Группы Ли и лежит в основе объединения электромагнитная сила и слабые силы (т.е.U (1) × SU (2)), а также квантовая хромодинамика, теория сильная сила (на основе SU (3)). Таким образом, это составляет основу нашего понимания Стандартная модель физики элементарных частиц.

История и теоретическое описание

В частной переписке Вольфганг Паули сформулировал в 1953 г. шестимерную теорию Полевые уравнения Эйнштейна из общая теория относительности, расширяя пятимерную теорию Калуца, Кляйн, Фок а другие - во внутреннее пространство более высоких измерений.^[1] Однако нет никаких доказательств того, что Паули разработал Лагранжиан из калибровочное поле или его квантование. Поскольку Паули обнаружил, что его теория «приводит к некоторым довольно нефизическим теневым частицам», он воздержался от официальной публикации своих результатов.^[1] Хотя Паули не опубликовал свою шестимерную теорию, он сделал два доклада по этому поводу в Цюрихе.^[2] Недавние исследования показывают, что расширенная теория Калуцы – Клейна в общем случае не эквивалентна теории Янга – Миллса, поскольку первая содержит дополнительные члены.^[3]

В начале 1954 г. Чен Нин Ян и Роберт Миллс^[4] расширил понятие калибровочной теории для абелевы группы, например квантовая электродинамика, неабелевым группам, чтобы объяснить сильные взаимодействия. Идею Янга-Миллса раскритиковал Паули,^[5] как кванты поля Янга – Миллса должны быть безмассовыми, чтобы калибровочная инвариантность. Идея была отложена до 1960 года, когда концепция частиц, приобретающих массу за счет нарушение симметрии в безмассовых теориях. Джеффри Голдстоун, Ёитиро Намбу, и Джованни Йона-Лазинио.

Это вызвало значительный перезапуск исследований теории Янга – Миллса, которые оказались успешными в формулировке обеих электрослабое объединение и квантовая хромодинамика (КХД). Электрослабое взаимодействие описывается калибровочной группой SU (2) × U (1), а КХД представляет собой SU (3) Теория Янга – Миллса. Безмассовые калибровочные бозоны электрослабого SU (2) × U (1) перемешиваются после спонтанное нарушение симметрии чтобы произвести 3 массивных слабых бозона (
W⁺
,
W⁻
, и
Z
), а также безмассовый фотон поле. Динамика фотонного поля и его взаимодействия с веществом, в свою очередь, регулируются калибровочной теорией квантовой электродинамики U (1). В Стандартная модель объединяет сильное взаимодействие с единым электрослабым взаимодействием (объединяющим слабый и электромагнитное взаимодействие ) через группу симметрий SU (3) × SU (2) × U (1). В современную эпоху сильное взаимодействие связывают не с электрослабым взаимодействием, а с наблюдаемым ход муфты константы считается^{[нужна цитата ]} все они сходятся к одному значению при очень высоких энергиях.

Феноменология при более низких энергиях в квантовой хромодинамике полностью не изучен из-за трудностей управления такой теорией с сильной связью. Это может быть причиной того, почему заключение не было теоретически доказано, хотя это последовательное экспериментальное наблюдение. Это показывает, почему удержание КХД при низкой энергии представляет собой математическую проблему большой важности и почему Существование Янга – Миллса и разрыв масс проблема это Проблема Премии тысячелетия.

Математический обзор

Теории Янга – Миллса являются частными примерами калибровочных теорий с неабелевой группой симметрии, задаваемой Лагранжиан

${ displaystyle { mathcal {L}} _ { mathrm {gf}} = - { frac {1} {2}} operatorname {Tr} (F ^ {2}) = - { frac {1} {4}} F ^ {a mu nu} F _ { mu nu} ^ {a}}$

с генераторами ${ displaystyle T ^ {a}}$ из Алгебра Ли, проиндексировано а, соответствующий F-количества ( кривизна или форма напряженности поля) удовлетворяющая

${ displaystyle operatorname {Tr} (T ^ {a} T ^ {b}) = { frac {1} {2}} delta ^ {ab}, quad [T ^ {a}, T ^ { b}] = если ^ {abc} T ^ {c}.}$

Здесь ж^abc находятся структурные константы алгебры Ли (полностью антисимметричной, если образующие алгебры Ли нормированы так, что ${ displaystyle Tr (T ^ {a} T ^ {b})}$ пропорционально ${ displaystyle delta ^ {ab}}$), ковариантная производная определяется как

${ displaystyle D _ { mu} = I partial _ { mu} -igT ^ {a} A _ { mu} ^ {a},}$

я это единичная матрица (соответствует размеру генераторов), ${ Displaystyle А _ { mu} ^ {а}}$ это вектор потенциал, и г это константа связи. В четырех измерениях константа связи г - чистое число, а для SU (N) первая группа ${ displaystyle a, b, c = 1 ldots N ^ {2} -1.}$

Соотношение

${ Displaystyle F _ { mu nu} ^ {a} = partial _ { mu} A _ { nu} ^ {a} - partial _ { nu} A _ { mu} ^ {a} + gf ^ {abc} A _ { mu} ^ {b} A _ { nu} ^ {c}}$

можно вывести коммутатор

${ displaystyle [D _ { mu}, D _ { nu}] = - igT ^ {a} F _ { mu nu} ^ {a}.}$

Поле обладает свойством самовзаимодействия, и получаемые уравнения движения называются полулинейными, поскольку нелинейности бывают как с производными, так и без них. Это означает, что управлять этой теорией можно только теория возмущений с небольшими нелинейностями.

Обратите внимание, что переход между «верхним» («контравариантным») и «нижним» («ковариантным») компонентами вектора или тензора является тривиальным для а индексы (например, ${ displaystyle f ^ {abc} = f_ {abc}}$), тогда как для μ и ν это нетривиально, что соответствует, например, к обычной подписи Лоренца, ${ displaystyle eta _ { mu nu} = { rm {diag}} (+ ---)}$.

Из данного лагранжиана можно вывести уравнения движения:

${ displaystyle partial ^ { mu} F _ { mu nu} ^ {a} + gf ^ {abc} A ^ { mu b} F _ { mu nu} ^ {c} = 0.}$

Положив ${ Displaystyle F _ { mu nu} = T ^ {a} F _ { mu nu} ^ {a}}$, их можно переписать как

${ displaystyle (D ^ { mu} F _ { mu nu}) ^ {a} = 0.}$

А Бьянки идентичность держит

${ displaystyle (D _ { mu} F _ { nu kappa}) ^ {a} + (D _ { kappa} F _ { mu nu}) ^ {a} + (D _ { nu} F _ { каппа му}) ^ {а} = 0}$

что эквивалентно Личность Якоби

${ displaystyle [D _ { mu}, [D _ { nu}, D _ { kappa}]] + [D _ { kappa}, [D _ { mu}, D _ { nu}]] + [D_ { nu}, [D _ { kappa}, D _ { mu}]] = 0}$

поскольку ${ Displaystyle [D _ { mu}, F _ { nu kappa} ^ {a}] = D _ { mu} F _ { nu kappa} ^ {a}}$. Определить двойной тензор силы${ displaystyle { tilde {F}} ^ { mu nu} = { frac {1} {2}} varepsilon ^ { mu nu rho sigma} F _ { rho sigma}}$, то тождество Бьянки можно переписать как

${ displaystyle D _ { mu} { tilde {F}} ^ { mu nu} = 0.}$

Источник ${ displaystyle J _ { mu} ^ {a}}$ входит в уравнения движения как

${ displaystyle partial ^ { mu} F _ { mu nu} ^ {a} + gf ^ {abc} A ^ {b mu} F _ { mu nu} ^ {c} = - J _ { nu} ^ {a}.}$

Обратите внимание, что токи должны правильно изменяться при преобразованиях группы датчиков.

Дадим здесь несколько комментариев о физических размерах муфты. В D размеры, поле масштабируется как ${ displaystyle [A] = [L ^ { frac {2-D} {2}}]}$^{[нужна цитата ]} и поэтому муфта должна масштабироваться как ${ Displaystyle [г ^ {2}] = [L ^ {D-4}]}$. Это означает, что теория Янга – Миллса не перенормируемый для размеров больше четырех. Кроме того, для D = 4, связь безразмерна, и поле и квадрат связи имеют одинаковые размеры поля и связи безмассовой квартики. скалярная теория поля. Итак, эти теории разделяют масштабная инвариантность на классическом уровне.

Квантование

Метод квантования теории Янга – Миллса - это функциональные методы, т.е. интегралы по путям. Один вводит производящий функционал для п-точечные функции как

${ displaystyle Z [j] = int [dA] exp left [- { frac {i} {2}} int d ^ {4} x operatorname {Tr} (F ^ { mu nu } F _ { mu nu}) + i int d ^ {4} x , j _ { mu} ^ {a} (x) A ^ {a mu} (x) right],}$

но этот интеграл не имеет смысла, потому что потенциальный вектор может быть выбран произвольно из-за свобода измерения. Эта проблема уже была известна в квантовой электродинамике, но здесь она становится более серьезной из-за неабелевых свойств калибровочной группы. Выход дал Людвиг Фаддеев и Виктор Попов с введением призрачное поле (увидеть Призрак Фаддеева – Попова ), который имеет свойство быть нефизическим, поскольку, хотя он согласуется с Статистика Ферми – Дирака, это комплексное скалярное поле, нарушающее спин-статистическая теорема. Итак, мы можем записать производящий функционал как

${ displaystyle { begin {align} Z [j, { bar { varepsilon}}, varepsilon] & = int [dA] [d { bar {c}}] [dc] exp left {iS_ {F} [ partial A, A] + iS_ {gf} [ partial A] + iS_ {g} [ partial c, partial { bar {c}}, c, { bar {c} }, A] right } & exp left {i int d ^ {4} xj _ { mu} ^ {a} (x) A ^ {a mu} (x) + i int d ^ {4} x [{ bar {c}} ^ {a} (x) varepsilon ^ {a} (x) + { bar { varepsilon}} ^ {a} (x) c ^ { а} (х)] право } конец {выровнено}}}$

будучи

${ displaystyle S_ {F} = - { frac {1} {2}} int operatorname {d} ! ^ {4} x operatorname {Tr} (F ^ { mu nu} F _ { му ню})}$

для поля,

${ displaystyle S_ {gf} = - { frac {1} {2 xi}} int operatorname {d} ! ^ {4} x ( partial cdot A) ^ {2}}$

для крепления датчика и

${ displaystyle S_ {g} = - int operatorname {d} ! ^ {4} x ({ bar {c}} ^ {a} partial _ { mu} partial ^ { mu} c ^ {a} + g { bar {c}} ^ {a} f ^ {abc} partial _ { mu} A ^ {b mu} c ^ {c})}$

для призрака. Это выражение обычно используется для вывода правил Фейнмана (см. Диаграмма Фейнмана ). Здесь у нас есть c^а для фантомного поля, а ξ фиксирует выбор калибровки для квантования. Правила Фейнмана, полученные из этого функционала, следующие:

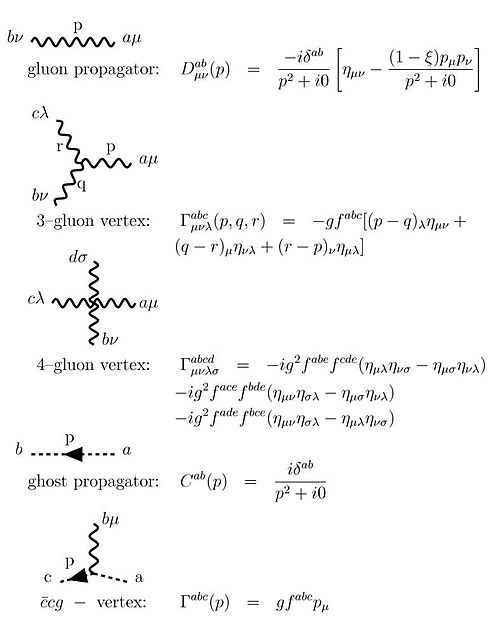
Эти правила для диаграмм Фейнмана могут быть получены, когда производящий функционал, приведенный выше, переписывается как

${ Displaystyle { begin {align} Z [j, { bar { varepsilon}}, varepsilon] & = exp left (-ig int d ^ {4} x , { frac { delta } {i delta { bar { varepsilon}} ^ {a} (x)}} f ^ {abc} partial _ { mu} { frac {i delta} { delta j _ { mu} ^ {b} (x)}} { frac {i delta} { delta varepsilon ^ {c} (x)}} right) & qquad times exp left (-ig int d ^ {4} xf ^ {abc} partial _ { mu} { frac {i delta} { delta j _ { nu} ^ {a} (x)}} { frac {i delta} { delta j _ { mu} ^ {b} (x)}} { frac {i delta} { delta j ^ {c nu} (x)}} right) & qquad qquad times exp left (-i { frac {g ^ {2}} {4}} int d ^ {4} xf ^ {abc} f ^ {ars} { frac {i delta} { delta j _ { mu} ^ {b} (x)}} { frac {i delta} { delta j _ { nu} ^ {c} (x)}} { frac {i delta} { delta j ^ {r mu} (x)}} { frac {i delta} { delta j ^ {s nu} (x)}} right) & qquad qquad qquad times Z_ {0} [j, { bar { varepsilon}}, varepsilon] end {align}}}$

с участием

${ displaystyle Z_ {0} [j, { bar { varepsilon}}, varepsilon] = exp left (- int d ^ {4} xd ^ {4} y { bar { varepsilon}} ^ {a} (x) C ^ {ab} (xy) varepsilon ^ {b} (y) right) exp left ({ tfrac {1} {2}} int d ^ {4} xd ^ {4} yj _ { mu} ^ {a} (x) D ^ {ab mu nu} (xy) j _ { nu} ^ {b} (y) right)}$

являясь производящим функционалом свободной теории. Расширение в г и вычисление функциональные производные, мы можем получить все п-точечные функции с теорией возмущений. С помощью Формула восстановления LSZ мы получаем от п-точечные функции соответствующие амплитуды процесса, поперечные сечения и скорость распада. Теория перенормируема, и поправки конечны при любом порядке теории возмущений.

Для квантовой электродинамики фантомное поле отделяется, потому что калибровочная группа абелева. Это видно из связи между калибровочным полем и фантомным полем, которое ${ displaystyle { bar {c}} ^ {a} f ^ {abc} partial _ { mu} A ^ {b mu} c ^ {c}}$. Для абелевого случая все структурные константы ${ displaystyle f ^ {abc}}$ равны нулю, поэтому связи нет. В неабелевом случае фантомное поле оказывается полезным способом переписать квантовую теорию поля без физических последствий для наблюдаемых в теории, таких как сечения или скорости распада.

Одним из наиболее важных результатов, полученных в теории Янга – Миллса, является асимптотическая свобода. Этот результат может быть получен, если предположить, что константа связи г мала (такие малые нелинейности), как для высоких энергий, и применяя теория возмущений. Актуальность этого результата связана с тем, что теория Янга – Миллса, описывающая сильное взаимодействие и асимптотическую свободу, допускает правильную обработку экспериментальных результатов, полученных из глубоконеупругое рассеяние.

Чтобы получить поведение теории Янга – Миллса при высоких энергиях и, таким образом, доказать асимптотическую свободу, применяется теория возмущений в предположении малой связи. Это проверено апостериорный в предел ультрафиолета. В противоположном пределе, инфракрасном пределе, ситуация противоположная, поскольку связь слишком велика, чтобы теория возмущений была надежной. Большинство трудностей, с которыми сталкиваются исследования, - это просто управление теорией при низких энергиях. Это интересный случай, присущий описанию адронной материи и, в более общем плане, всем наблюдаемым связанным состояниям глюонов и кварков и их ограничению (см. адроны ). Наиболее часто используемый метод изучения теории в этом пределе - попытка решить ее на компьютере (см. решеточная калибровочная теория ). В этом случае требуются большие вычислительные ресурсы, чтобы гарантировать получение правильного предела бесконечного объема (меньший интервал решетки). Это предел, с которым нужно сравнивать результаты. Меньший интервал и большая связь не независимы друг от друга, и для каждого требуются большие вычислительные ресурсы. На сегодняшний день ситуация кажется удовлетворительной для адронного спектра и расчета пропагаторов глюонов и духов, но глюбол и гибриды спектры пока еще остаются под вопросом в связи с экспериментальным наблюдением таких экзотических состояний. Действительно, σ-резонанс^[6][7] не наблюдается ни в одном из таких вычислений на решетке, и были выдвинуты противоположные интерпретации. Это горячо обсуждаемый вопрос.

Открытые проблемы

Теории Янга – Миллса получили всеобщее признание в физическом сообществе после Жерар т Хофт в 1972 г. разработал их перенормировку, опираясь на постановку задачи, разработанную его советником. Мартинус Вельтман.^[8] Перенормируемость достигается даже в том случае, если калибровочные бозоны, описываемые этой теорией, являются массивными, как в электрослабой теории, при условии, что масса только «приобретенная», порожденная Механизм Хиггса.

Математика теории Янга – Миллса - очень активная область исследований, в результате чего, например, инвариантов дифференцируемых структур на четырехмерных многообразиях с помощью работы Саймон Дональдсон. Кроме того, область теорий Янга – Миллса была включена в Институт математики Клэя список "Задачи Премии тысячелетия Здесь проблема приза состоит, в частности, в доказательстве гипотезы о том, что низшие возбуждения чистой теории Янга – Миллса (т. Е. Без полей материи) имеют конечную запрещенную массу по отношению к вакуумному состоянию. Другая открытая проблема , связанное с этой гипотезой, является доказательством заключение свойство в присутствии дополнительных частиц фермиона.

В физике обзор теорий Янга – Миллса обычно начинается не с анализа возмущений или аналитических методов, а в последнее время с систематического применения численных методов к решеточные калибровочные теории.

Смотрите также

использованная литература

дальнейшее чтение

Книги

• Фрэмптон, П. (2008). Теории калибровочного поля (3-е изд.). Вайли-ВЧ. ISBN  978-3-527-40835-1.
• Cheng, T.-P .; Ли, Л.-Ф. (1983). Калибровочная теория физики элементарных частиц. Oxford University Press. ISBN  0-19-851961-3.
• 'т Хофт, Герард, изд. (2005). 50 лет теории Янга – Миллса. Сингапур: Всемирный научный. ISBN  981-238-934-2.

Статьи

• Светличный, Георгий (1999). «Подготовка к калибровочной теории». arXiv:math-ph / 9902027.
• Гросс, Д. (1992). «Калибровочная теория - прошлое, настоящее и будущее». Получено 2015-05-05.

внешние ссылки

• "Поле Янга-Миллса", Энциклопедия математики, EMS Press, 2001 [1994]
• Теория Янга – Миллса на DispersiveWiki
• Институт математики Клэя
• Проблемы Премии тысячелетия