Квантовая электродинамика - Википедия - Quantum electrodynamics

Квантовая теория поля
Диаграмма Фейнмана
История
Фон Теория поля Электромагнетизм Слабая сила Сильная сила Квантовая механика Специальная теория относительности Общая теория относительности Калибровочная теория
Симметрии Симметрия в квантовой механике C-симметрия P-симметрия Т-симметрия Симметрия переноса пространства Симметрия перевода времени Симметрия вращения Симметрия Лоренца Симметрия Пуанкаре Калибровочная симметрия Явное нарушение симметрии Спонтанное нарушение симметрии Теория Янга – Миллса Нётер заряд Топологический заряд
Инструменты Аномалия Переход Эффективная теория поля Ценность ожидания Призрачные поля Призраки Фаддеева – Попова Диаграмма Фейнмана Решеточная калибровочная теория Формула восстановления LSZ Функция разделения Пропагатор Квантование Регуляризация Перенормировка Состояние вакуума Теорема Вика Аксиомы Вайтмана Параметризация Фейнмана
Уравнения Уравнение Дирака Уравнение Клейна – Гордона Уравнения Прока Уравнение Уиллера – ДеВитта Уравнения Баргмана – Вигнера Уравнение Джооса – Вайнберга Уравнение Вейля
Стандартная модель Квантовое вакуумное состояние Квантовая динамика Квантовая термодинамика Квантовая электродинамика Электрослабое взаимодействие Квантовая хромодинамика Механизм Хиггса Виртуальная частица
Неполные теории Причинная динамическая триангуляция Причинные фермионные системы Причинные множества Конформная теория поля Море Дирака Теория возмущений Двумерная конформная теория поля Квантовая теория поля в искривленном пространстве-времени Теория теплового квантового поля Топологическая квантовая теория поля Квантовая геометрия Полуклассическая гравитация Отжим пена Теория струн Теория суперструн М-Теория Суперсимметрия Супергравитация Разноцветный Теория всего Каноническая квантовая гравитация Квантовая гравитация Петлевая квантовая гравитация Петлевая квантовая космология Теория скрытых переменных Теория объективного коллапса
Ученые Адлер Андерсон Быть Боголюбов Коулман Каллан ДеВитт Дирак Дайсон Ферми Фейнман Фирц Фок Fröhlich Гелл-Манн Голдстоун Валовой Гейзенберг 'т Хофт Джеки Иордания Ландо Ли Lehmann Мандельштам Майорана Намбу Паризи Поляков Салам Швингер Skyrme Штюкельберг Симанзик Томонага Вельтман Вайнберг Weisskopf Weyl Вильчек Уилсон Виттен Ян Юкава Циммерманн Зинн-Джастин

В физике элементарных частиц квантовая электродинамика (QED) это релятивистский квантовая теория поля из электродинамика. По сути, он описывает, как свет и иметь значение взаимодействуют, и это первая теория, в которой полное согласие между квантовая механика и специальная теория относительности Достигнут. QED математически описывает все явления с участием электрически заряженный частицы, взаимодействующие посредством обмена фотоны и представляет собой квант аналог классический электромагнетизм дающий полный отчет о взаимодействии материи и света.

Технически QED можно описать как теория возмущений электромагнитного квантовый вакуум. Ричард Фейнман назвал его "жемчужиной физики" за его чрезвычайно точные прогнозы таких величин, как аномальный магнитный момент электрона и Баранина сдвиг из уровни энергии из водород.^[1]:Ch1

История

Поль Дирак

Первая формулировка квантовая теория описание взаимодействия излучения и вещества приписывается британскому ученому Поль Дирак, который (в течение 1920-х гг.) смог вычислить коэффициент спонтанное излучение из атом.^[2]

Дирак описал квантование электромагнитное поле как ансамбль гармонические осцилляторы с введением концепции операторы создания и уничтожения частиц. В последующие годы при участии Вольфганг Паули, Юджин Вигнер, Паскуаль Джордан, Вернер Гейзенберг и элегантная формулировка квантовой электродинамики благодаря Энрико Ферми,^[3] физики пришли к выводу, что в принципе можно выполнить любые вычисления для любого физического процесса, включающего фотоны и заряженные частицы. Однако дальнейшие исследования Феликс Блох с Арнольд Нордзик,^[4] и Виктор Вайскопф,^[5] в 1937 и 1939 годах, показали, что такие вычисления были надежными только при первом порядке теория возмущений, проблема уже отмечена Роберт Оппенгеймер.^[6] На более высоких порядках в серии появлялись бесконечности, делающие такие вычисления бессмысленными и вызывающие серьезные сомнения во внутренней непротиворечивости самой теории. Поскольку в то время не было известно решения этой проблемы, оказалось, что существует фундаментальная несовместимость между специальная теория относительности и квантовая механика.

Ганс Бете

Трудности с теорией увеличились до конца 1940-х годов. Улучшения в микроволновая печь технология позволила проводить более точные измерения смещения уровней атом водорода,^[7] теперь известный как Баранина сдвиг и магнитный момент электрона.^[8] Эти эксперименты выявили расхождения, которые теория не могла объяснить.

Первое указание на возможный выход было дано Ганс Бете в 1947 г.,^[9] после посещения Конференция острова Шелтер.^[10] Пока он ехал поездом с конференции в Скенектади он провел первое нерелятивистское вычисление сдвига линий атома водорода, измеренного Лэмбом и Retherford.^[9] Несмотря на ограничения вычислений, согласие было отличным. Идея заключалась в том, чтобы просто прикрепить бесконечность к исправлениям масса и обвинять которые фактически были зафиксированы экспериментами до конечного значения. Таким образом, бесконечности поглощаются этими константами и дают конечный результат, хорошо согласующийся с экспериментом. Эта процедура получила название перенормировка.

Фейнман (в центре) и Оппенгеймер (справа) в Лос-Аламос.

На основе интуиции Бете и фундаментальных работ по этому вопросу автора Синъитиро Томонага,^[11] Джулиан Швингер,^[12][13] Ричард Фейнман^[14][15][16] и Фриман Дайсон,^[17][18] наконец стало возможно получить полностью ковариантный формулировок, конечных в любом порядке в серии возмущений квантовой электродинамики. Синъитиро Томонага, Джулиан Швингер и Ричард Фейнман были совместно награждены орденом 1965 г. Нобелевская премия по физике за их работу в этой области.^[19] Их вклад и вклад Фриман Дайсон, были около ковариантный и калибровочно-инвариантный формулировки квантовой электродинамики, которые позволяют вычислять наблюдаемые в любом порядке теория возмущений. Математический метод Фейнмана, основанный на его диаграммы, поначалу казался очень отличным от теоретико-полевого, оператор основанный на подходе Швингера и Томонаги, но Фриман Дайсон позже показал, что эти два подхода эквивалентны.^[17] Перенормировка, необходимость придания физического смысла некоторым расхождениям, возникающим в теории, через интегралы, впоследствии стал одним из фундаментальных аспектов квантовая теория поля и стал рассматриваться как критерий общей приемлемости теории. Несмотря на то, что на практике перенормировка работает очень хорошо, Фейнман никогда не чувствовал себя полностью уверенным в ее математической достоверности, даже говоря о перенормировке как о «игре в ракушки» и «фокус-покусе».^[1]:128

КЭД послужила моделью и шаблоном для всех последующих квантовых теорий поля. Одна из таких последующих теорий квантовая хромодинамика, которая началась в начале 1960-х годов и достигла своего нынешнего вида в 1970-х годах. Х. Дэвид Политцер, Сидни Коулман, Дэвид Гросс и Франк Вильчек. Основываясь на новаторской работе Швингер, Джеральд Гуральник, Дик Хаген, и Том Киббл,^[20][21] Питер Хиггс, Джеффри Голдстоун, и другие, Шелдон Ли Глэшоу, Стивен Вайнберг и Абдус Салам независимо показал, как слабая ядерная сила и квантовую электродинамику можно было бы объединить в единую электрослабая сила.

Взгляд Фейнмана на квантовую электродинамику

Вступление

Ближе к концу своей жизни Ричард Фейнман прочитал серию лекций по QED, предназначенных для широкой публики. Эти лекции были переписаны и опубликованы как Feynman (1985), QED: странная теория света и материи,^[1] классическое нематематическое изложение КЭД с точки зрения, сформулированной ниже.

Ключевыми компонентами представления КЭД Фейнманом являются три основных действия.^[1]:85

А фотон переходит из одного места и времени в другое место и время.

An электрон переходит из одного места и времени в другое место и время.

Электрон излучает или поглощает фотон в определенном месте и в определенное время.

Диаграмма Фейнмана элементы

Эти действия представлены в виде визуального сокращения тремя основными элементами Диаграммы Фейнмана: волнистая линия для фотона, прямая линия для электрона и соединение двух прямых линий и волнистая линия для вершины, представляющей излучение или поглощение фотона электроном. Все это можно увидеть на диаграмме рядом.

Помимо визуального обозначения действий, Фейнман вводит еще один вид сокращения для числовых величин, называемый амплитуды вероятности. Вероятность - это квадрат абсолютного значения полной амплитуды вероятности, ${ Displaystyle { текст {вероятность}} = | е ({ текст {амплитуда}}) | ^ {2}}$. Если фотон движется из одного места и времени ${ displaystyle A}$ в другое место и время ${ displaystyle B}$связанная величина записывается в сокращении Фейнмана как ${ displaystyle P (A { text {to}} B)}$. Аналогичная величина для электрона, движущегося из ${ displaystyle C}$ к ${ displaystyle D}$ написано ${ displaystyle E (C { text {to}} D)}$. Величина, которая говорит нам об амплитуде вероятности излучения или поглощения фотона, которую он называет j. Это связано с измеренным заряд электрона е.^[1]:91

КЭД основана на предположении, что сложные взаимодействия множества электронов и фотонов могут быть представлены путем подбора подходящего набора из трех вышеуказанных строительных блоков и последующего использования амплитуд вероятности для вычисления вероятности любого такого сложного взаимодействия. Оказывается, что основная идея КЭД может быть передана, если предположить, что квадрат суммы амплитуд вероятностей, упомянутых выше (п(А к B), E(C к D) и j) действует как наш повседневный вероятность (упрощение, сделанное в книге Фейнмана). Позже, вслед за Фейнманом, это будет исправлено, чтобы включить в него математику квантового стиля.

Основные правила амплитуд вероятности, которые будут использоваться, следующие:^[1]:93

Основные конструкции

Предположим, мы начинаем с одного электрона в определенном месте и в определенное время (этому месту и времени присвоено произвольное обозначение А) и фотон в другом месте и в другое время (учитывая метку B). Типичный вопрос с физической точки зрения: «Какова вероятность найти электрон при C (другое место и более позднее время) и фотон в D (еще одно место и время)? ». Самым простым способом достижения этой цели является перемещение электрона из А к C (элементарное действие) и для движения фотона из B к D (еще одно элементарное действие). Зная амплитуды вероятностей каждого из этих подпроцессов - E(А к C) и п(B к D) - мы ожидаем вычислить амплитуду вероятности того, что оба события произойдут вместе, умножив их, используя правило b) выше. Это дает простую оценочную общую амплитуду вероятности, которая возводится в квадрат для получения оценочной вероятности.^{[нужна цитата ]}

Комптоновское рассеяние

Но есть и другие способы достижения конечного результата. Электрон может переместиться в место и время E, где он поглощает фотон; затем двигайтесь дальше, прежде чем испустить еще один фотон на F; затем переходите к C, где он обнаруживается, а новый фотон движется к D. Вероятность этого сложного процесса можно снова рассчитать, зная амплитуды вероятности каждого из отдельных действий: трех воздействий электронов, двух воздействий фотонов и двух вершин - одного излучения и одного поглощения. Мы ожидаем найти полную амплитуду вероятности, умножив амплитуды вероятности каждого из действий для любых выбранных позиций E и F. Затем, используя правило а) выше, мы должны сложить все эти амплитуды вероятностей для всех альтернатив для E и F. (На практике это не элементарно и предполагает интеграция.) Но есть и другая возможность: электрон сначала движется в грамм, где он испускает фотон, который переходит в D, а электрон переходит на ЧАС, где он поглощает первый фотон, прежде чем перейти к C. Опять же, мы можем вычислить амплитуду вероятности этих возможностей (для всех точек грамм и ЧАС). Затем мы получаем лучшую оценку общей амплитуды вероятности, добавляя амплитуды вероятностей этих двух возможностей к нашей первоначальной простой оценке. Между прочим, этот процесс взаимодействия фотона с электроном таким образом получил название Комптоновское рассеяние.^{[нужна цитата ]}

Существует бесконечное число других промежуточных процессов, в которых все больше и больше фотонов поглощается и / или испускается. Для каждой из этих возможностей есть диаграмма Фейнмана, описывающая ее. Это подразумевает сложное вычисление результирующих амплитуд вероятности, но при условии, что чем сложнее диаграмма, тем меньше она влияет на результат, это всего лишь вопрос времени и усилий, чтобы найти такой точный ответ, который нужен. к исходному вопросу. Это основной подход QED. Для расчета вероятности любой Интерактивный процесс между электронами и фотонами, с диаграммами Фейнмана нужно сначала отметить все возможные способы, которыми процесс может быть построен из трех основных элементов. Каждая диаграмма включает в себя некоторые вычисления, включающие определенные правила, чтобы найти соответствующую амплитуду вероятности.

Этот базовый каркас остается при переходе к квантовому описанию, но необходимы некоторые концептуальные изменения. Во-первых, в то время как в повседневной жизни мы можем ожидать, что будут некоторые ограничения на точки, в которые может двигаться частица, то есть нет верно в полной квантовой электродинамике. Есть возможность электрона на А, или фотон на B, переходя как основное действие в любое другое место и время во вселенной. Это включает в себя места, которые можно было достичь только со скоростью большей, чем скорость света, а также прежние времена. (Электрон, движущийся назад во времени, можно рассматривать как позитрон продвигаясь вперед во времени.)^{[1]:89, 98–99}

Амплитуды вероятности

Фейнман заменяет комплексные числа вращающимися стрелками, которые начинаются при испускании и заканчиваются при обнаружении частицы. Сумма всех полученных стрелок представляет собой общую вероятность события. На этой диаграмме свет, излучаемый источником S отскакивает от нескольких сегментов зеркала (синего цвета), прежде чем достигнет детектора на п. Необходимо учитывать сумму всех путей. На графике ниже показано общее время, затраченное на прохождение каждого из указанных выше путей.

Квантовая механика вносит важное изменение в способ вычисления вероятностей. Вероятности по-прежнему представлены обычными действительными числами, которые мы используем для вероятностей в нашем повседневном мире, но вероятности вычисляются как квадратный модуль амплитуды вероятности, которые сложные числа.

Фейнман избегает знакомить читателя с математикой комплексных чисел, используя простое, но точное представление их в виде стрелок на листе бумаги или экране. (Их не следует путать со стрелками диаграмм Фейнмана, которые представляют собой упрощенные представления в двух измерениях отношений между точками в трех измерениях пространства и одном временном.) Стрелки амплитуды имеют фундаментальное значение для описания мира, задаваемого квантовым теория. Они связаны с нашими повседневными представлениями о вероятности простым правилом: вероятность события - это квадрат длины соответствующей стрелки амплитуды. Итак, для данного процесса, если две амплитуды вероятности, v и ш, вовлечены, вероятность процесса будет определяться либо

${ Displaystyle P = | mathbf {v} + mathbf {w} | ^ {2}}$

или же

${ Displaystyle P = | mathbf {v} , mathbf {w} | ^ {2}.}$

Однако правила сложения и умножения такие же, как и выше. Но там, где вы ожидаете сложить или умножить вероятности, вместо этого вы складываете или умножаете амплитуды вероятностей, которые теперь являются комплексными числами.

Сложение амплитуд вероятностей в виде комплексных чисел

Умножение амплитуд вероятности на комплексные числа

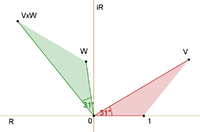
Сложение и умножение - обычные операции в теории комплексных чисел, которые показаны на рисунках. Сумма находится следующим образом. Пусть начало второй стрелки будет в конце первой. Сумма представляет собой третью стрелку, идущую прямо от начала первой до конца второй. Произведение двух стрелок - это стрелка, длина которой равна произведению двух длин. Направление продукта определяется путем добавления углов, что каждый из этих двух были повернут на относительно опорное направление: что дает угол, что устройство включено относительно опорного направления.

Это изменение от вероятностей к амплитудам вероятностей усложняет математику без изменения основного подхода. Но этого изменения все еще недостаточно, потому что при этом не учитывается тот факт, что и фотоны, и электроны могут быть поляризованными, то есть их ориентацию в пространстве и времени необходимо учитывать. Следовательно, п(А к B) состоит из 16 комплексных чисел или стрелок амплитуды вероятности.^{[1]:120–121} Также есть небольшие изменения, связанные с количеством j, который, возможно, придется повернуть на 90 ° для некоторых поляризаций, что представляет интерес только для подробного учета.

С тем, что электрон может быть поляризован, связана еще одна небольшая необходимая деталь, связанная с тем, что электрон - это фермион и подчиняется Статистика Ферми – Дирака. Основное правило состоит в том, что если у нас есть амплитуда вероятности для данного сложного процесса с участием более чем одного электрона, то, когда мы включаем (как мы всегда должны) дополнительную диаграмму Фейнмана, в которой мы обмениваемся двумя электронными событиями, результирующая амплитуда обратная - отрицательный - первого. В простейшем случае два электрона начинаются с А и B заканчивается в C и D. Амплитуда будет рассчитана как «разница», E(А к D) × E(B к C) − E(А к C) × E(B к D), где мы ожидаем, исходя из нашего повседневного представления о вероятностях, что это будет сумма.^{[1]:112–113}

Пропагаторы

Наконец, нужно вычислить п(А к B) и E(C к D), соответствующие амплитудам вероятности для фотона и электрона соответственно. По сути, это решения Уравнение Дирака, которые описывают поведение амплитуды вероятности электрона и Уравнения Максвелла, который описывает поведение амплитуды вероятности фотона. Они называются Пропагаторы Фейнмана. Перевод в систему обозначений, обычно используемых в стандартной литературе, выглядит следующим образом:

${ displaystyle P (A { text {to}} B) to D_ {F} (x_ {B} -x_ {A}), quad E (C { text {to}} D) to S_ {F} (x_ {D} -x_ {C}),}$

где сокращенный символ, такой как ${ displaystyle x_ {A}}$ обозначает четыре действительных числа, которые показывают время и положение в трех измерениях точки, помеченной А.

Массовая перенормировка

Собственная энергия электрона петля

Исторически возникла проблема, которая задерживала прогресс на двадцать лет: хотя мы начинаем с предположения о трех основных «простых» действиях, правила игры гласят, что если мы хотим вычислить амплитуду вероятности выхода электрона из А к B, мы должны учитывать все возможные пути: все возможные диаграммы Фейнмана с этими конечными точками. Таким образом, электрон будет перемещаться в C, испускает фотон здесь и снова поглощает его на D прежде чем перейти к B. Или он может делать такие вещи дважды или больше. Короче говоря, у нас есть фрактал -подобная ситуация, в которой, если мы внимательно посмотрим на строку, она распадается на набор «простых» строк, каждая из которых при внимательном рассмотрении, в свою очередь, состоит из «простых» линий и т. д. до бесконечности. Это сложная ситуация. Если бы добавление этой детали лишь немного изменило ситуацию, это было бы неплохо, но случилась катастрофа, когда было обнаружено, что упомянутое выше простое исправление привело к бесконечный амплитуды вероятностей. Со временем эта проблема была «исправлена» методом перенормировка. Однако сам Фейнман остался недоволен этим, назвав это «дурацким процессом».^[1]:128

Выводы

В рамках вышеупомянутой схемы физики смогли вычислить с высокой степенью точности некоторые свойства электронов, такие как аномальный магнитный дипольный момент. Однако, как указывает Фейнман, он не может объяснить, почему частицы, такие как электрон, обладают такой массой. «Не существует теории, которая адекватно объясняет эти числа. Мы используем числа во всех наших теориях, но мы не понимаем их - что они такое и откуда они взялись. Я считаю, что с фундаментальной точки зрения это очень интересная и серьезная проблема ».^[1]:152

Математическая формулировка

Математически QED - это абелевский калибровочная теория с группой симметрии U (1). В калибровочное поле, который опосредует взаимодействие заряженных спин-1/2 поля, это электромагнитное поле.QED Лагранжиан для поля спина 1/2 ${ displaystyle psi}$, ${ displaystyle A}$ взаимодействие с внешним электромагнитным полем ${ displaystyle B}$ выражается в натуральных единицах действительной частью^[22]:78

куда

${ displaystyle gamma ^ { mu}}$ находятся Матрицы Дирака;

${ displaystyle psi}$ а биспинор поле из спин-1/2 частицы (например, электрон –позитрон поле);

${ displaystyle { bar { psi}} Equiv psi ^ { dagger} gamma ^ {0}}$, называемый «пси-бар», иногда называют Дирак сопряженный;

${ Displaystyle D _ { mu} Equiv partial _ { mu} + ieA _ { mu} + ieB _ { mu} , !}$ это калибровочная ковариантная производная;

е это константа связи, равный электрический заряд биспинорного поля;

м - масса электрона или позитрона;

${ displaystyle A _ { mu}}$ это ковариантный четырехпотенциальный электромагнитного поля, создаваемого самим электроном и

${ Displaystyle F _ { mu nu} = partial _ { mu} A _ { nu} - partial _ { nu} A _ { mu} , !}$ связано с ним тензор электромагнитного поля;

${ displaystyle B _ { mu}}$ - внешнее поле, создаваемое внешним источником;

Подставляя определение D в лагранжиан и переставляя, его можно разложить на несколько элементов с определенными значениями:

${ Displaystyle { mathcal {L}} = (я { bar { psi}} gamma ^ { mu} partial _ { mu} psi -m { bar { psi}} psi) + (- e { bar { psi}} gamma ^ { mu} A _ { mu} psi - { frac {1} {4}} F _ { mu nu} F ^ { mu nu}) - e { bar { psi}} gamma ^ { mu} B _ { mu} psi.}$

где термины, заключенные в первые круглые скобки, соответствуют Лагранжиан Дирака для частицы со спином 1/2 члены во второй скобке соответствуют электромагнитный лагранжиан поля электрона, а последний член соответствует внешнему полю.

Уравнения движения

Подставляя определение D в лагранжиан дает

${ displaystyle { mathcal {L}} = я { bar { psi}} gamma ^ { mu} partial _ { mu} psi -e { bar { psi}} gamma ^ { mu} (A _ { mu} + B _ { mu}) psi -m { bar { psi}} psi - { frac {1} {4}} F _ { mu nu} F ^ { mu nu}.}$

Из этого лагранжиана уравнения движения для ψ и А поля можно получить.

• Используя теоретико-полевую Уравнение Эйлера – Лагранжа. за ψ,

${ displaystyle partial _ { mu} left ({ frac { partial { mathcal {L}}} { partial ( partial _ { mu} psi)}} right) - { frac { partial { mathcal {L}}} { partial psi}} = 0.}$

(2)

Производные лагранжиана относительно ψ находятся

${ displaystyle partial _ { mu} left ({ frac { partial { mathcal {L}}} { partial ( partial _ { mu} psi)}} right) = partial _ { mu} left (i { bar { psi}} gamma ^ { mu} right),}$

${ displaystyle { frac { partial { mathcal {L}}} { partial psi}} = - e { bar { psi}} gamma ^ { mu} (A _ { mu} + B_ { mu}) - m { bar { psi}}.}$

Вставив их в (2) приводит к

${ displaystyle i partial _ { mu} { bar { psi}} gamma ^ { mu} + e { bar { psi}} gamma ^ { mu} (A _ { mu} + B _ { mu}) + m { bar { psi}} = 0,}$

с Эрмитово сопряжение

${ Displaystyle я гамма ^ { му} partial _ { mu} psi -e gamma ^ { mu} (A _ { mu} + B _ { mu}) psi -m psi = 0 .}$

Перемещение среднего члена в правую часть дает

Левая часть как у оригинала Уравнение Дирака, а правая часть - взаимодействие с электромагнитным полем.

• Используя уравнение Эйлера – Лагранжа для А поле,

${ displaystyle partial _ { nu} left ({ frac { partial { mathcal {L}}} { partial ( partial _ { nu} A _ { mu})}} right) - { frac { partial { mathcal {L}}} { partial A _ { mu}}} = 0,}$

(3)

на этот раз производные

${ displaystyle partial _ { nu} left ({ frac { partial { mathcal {L}}} { partial ( partial _ { nu} A _ { mu})}} справа) = partial _ { nu} left ( partial ^ { mu} A ^ { nu} - partial ^ { nu} A ^ { mu} right),}$

${ displaystyle { frac { partial { mathcal {L}}} { partial A _ { mu}}} = - e { bar { psi}} gamma ^ { mu} psi.}$

Подставляя обратно в (3) приводит к

Теперь, если мы наложим Условие калибровки Лоренца

${ Displaystyle partial _ { mu} A ^ { mu} = 0,}$

уравнения сводятся к

${ displaystyle Box A ^ { mu} = e { bar { psi}} gamma ^ { mu} psi,}$

который является волновое уравнение для четырехпотенциала КЭД-версия классического Уравнения Максвелла в Датчик Лоренца. (Квадрат представляет Оператор Даламбера, ${ Displaystyle Box = partial _ { alpha} partial ^ { alpha}}$.)

Картинка взаимодействия

Эту теорию можно напрямую квантовать, рассматривая бозонные и фермионные секторы^{[требуется разъяснение ]} как бесплатно. Это позволяет нам построить набор асимптотических состояний, которые можно использовать для начала вычисления амплитуд вероятностей для различных процессов. Для этого мы должны вычислить оператор эволюции, которая для данного начального состояния ${ displaystyle | я rangle}$ даст окончательное состояние ${ displaystyle langle f |}$ таким образом иметь^[22]:5

${ displaystyle M_ {fi} = langle f | U | i rangle.}$

Этот метод также известен как S-матрица. Оператор эволюции получается в картинка взаимодействия, где временная эволюция задается гамильтонианом взаимодействия, который представляет собой интеграл по пространству от второго члена в плотности лагранжиана, приведенной выше:^[22]:123

${ Displaystyle V = е int d ^ {3} х , { bar { psi}} gamma ^ { mu} psi A _ { mu},}$

и так, есть^[22]:86

${ displaystyle U = T exp left [- { frac {i} { hbar}} int _ {t_ {0}} ^ {t} dt ', V (t') right],}$

куда Т это хронометраж оператор. Этот оператор эволюции имеет значение только как ряд, и здесь мы получаем ряд возмущений с постоянная тонкой структуры как параметр развития. Эта серия называется Серия Дайсон.

Диаграммы Фейнмана

Несмотря на концептуальную ясность этого подхода Фейнмана к КЭД, почти ни в одном из ранних учебников не последовало его изложение. При проведении расчетов гораздо проще работать с Преобразования Фурье из пропагаторы. Экспериментальные проверки квантовой электродинамики обычно представляют собой эксперименты по рассеянию. В теории рассеяния частицы импульсы рассматриваются не их положения, и удобно думать о частицах как о создаваемых или аннигилирующих при их взаимодействии. Тогда диаграммы Фейнмана Смотреть то же самое, но строки имеют разное толкование. Электронная линия представляет собой электрон с заданной энергией и импульсом, с аналогичной интерпретацией фотонной линии. Вершинная диаграмма представляет собой аннигиляцию одного электрона и создание другого вместе с поглощением или созданием фотона, каждый из которых имеет определенные энергии и импульсы.

С помощью Теорема Вика на условиях серии Дайсона все условия S-матрица для квантовой электродинамики можно вычислить с помощью техники Диаграммы Фейнмана. В этом случае правила рисования следующие.^{[22]:801–802}

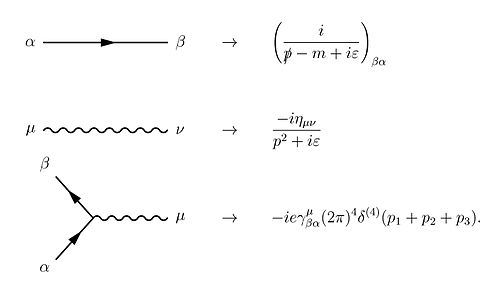
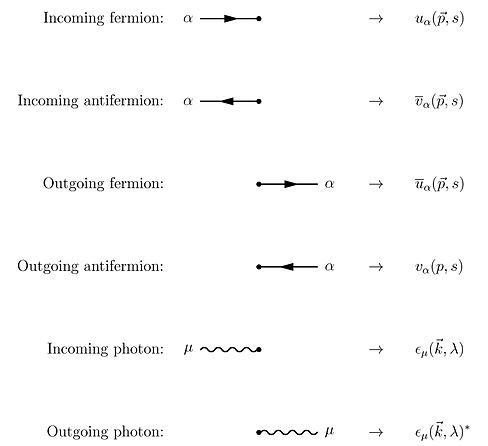
К этим правилам мы должны добавить еще одно для замкнутых контуров, которое подразумевает интегрирование по импульсам ${ displaystyle int d ^ {4} p / (2 pi) ^ {4}}$, поскольку эти внутренние ("виртуальные") частицы не ограничены какой-либо определенной энергией-импульсом, даже той, которая обычно требуется специальной теорией относительности (см. Пропагатор подробнее).

Из них вычисления амплитуды вероятности даются прямо. Примером является Комптоновское рассеяние, с электрон и фотон проходящий упругое рассеяние. Диаграммы Фейнмана в этом случае^{[22]:158–159}

и поэтому мы можем получить соответствующую амплитуду в первом порядке ряд возмущений для S-матрица:

${ displaystyle M_ {fi} = (т.е.) ^ {2} { overline {u}} ({ vec {p}} ', s') epsilon ! ! ! / , '({ vec {k}} ', lambda') ^ {*} { frac {p ! ! ! / + k ! ! ! / + m_ {e}} {(p + k) ^ { 2} -m_ {e} ^ {2}}} epsilon ! ! ! / ({ Vec {k}}, lambda) u ({ vec {p}}, s) + (т.е.) ^ {2} { overline {u}} ({ vec {p}} ', s') epsilon ! ! ! / ({ Vec {k}}, lambda) { frac {p ! ! ! / - к ! ! ! / '+ m_ {e}} {(p-k') ^ {2} -m_ {e} ^ {2}}} epsilon ! ! ! / , '({ vec {k}}', lambda ') ^ {*} u ({ vec {p}}, s),}$

из которого мы можем вычислить поперечное сечение для этого рассеяния.

Непертурбативные явления

Прогнозирующий успех квантовой электродинамики во многом основан на использовании теории возмущений, выраженной в диаграммах Фейнмана. Однако квантовая электродинамика также приводит к предсказаниям, выходящим за рамки теории возмущений. В присутствии очень сильных электрических полей он предсказывает, что электроны и позитроны будут спонтанно образовываться, вызывая распад поля. Этот процесс, названный Эффект Швингера,^[23] не может быть понят в терминах любого конечного числа диаграмм Фейнмана и, следовательно, описывается как непертурбативный. Математически это может быть получено полуклассическим приближением к интеграл по путям квантовой электродинамики.

Перенормируемость

Члены более высокого порядка могут быть напрямую вычислены для оператора эволюции, но эти члены отображают диаграммы, содержащие следующие более простые^{[22]:ch 10}

• 

  Однопетлевой вклад в поляризация вакуума функция ${ displaystyle Pi}$

• 

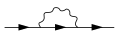
  Однопетлевой вклад в электрон собственная энергия функция ${ displaystyle Sigma}$

• 

  Однопетлевой вклад в вершинная функция ${ displaystyle Gamma}$

что, будучи замкнутыми контурами, подразумевает наличие расходящихся интегралы не имеющий математического значения. Чтобы преодолеть эту трудность, была использована техника, называемая перенормировка был разработан, давая конечные результаты в очень хорошем соответствии с экспериментами. Критерием осмысленности теории после перенормировки является конечное число расходящихся диаграмм. В этом случае теория называется «перенормируемой». Причина этого в том, что для перенормировки наблюдаемых требуется конечное число констант, чтобы сохранить предсказательную ценность теории неизменной. Это как раз тот случай, когда квантовая электродинамика отображает всего три расходящиеся диаграммы. Эта процедура дает наблюдаемые, которые очень хорошо согласуются с экспериментом, например, для электрона гиромагнитное отношение.

Перенормируемость стала важным критерием для квантовая теория поля считаться жизнеспособным. Все теории, описывающие фундаментальные взаимодействия, Кроме гравитация, квантовый аналог которых является только предположительным и в настоящее время очень активно исследуется, являются перенормируемыми теориями.

Несходимость рядов

Аргумент Фриман Дайсон показывает, что радиус схождения ряда возмущений в КЭД равна нулю.^[24] Основной аргумент заключается в следующем: если константа связи были отрицательными, это было бы эквивалентно Постоянная кулоновской силы быть отрицательным. Это "перевернет" электромагнитное взаимодействие так, что подобно обвинения будут привлекать и В отличие от обвинения будут отталкивать. Это сделало бы вакуум нестабильным по отношению к распаду на скопление электронов на одной стороне вселенной и скопление позитронов на другой стороне вселенной. Поскольку теория "больна" при любом отрицательном значении константы связи, ряды не сходятся, но в лучшем случае являются асимптотический ряд.

С современной точки зрения мы говорим, что КЭД не может быть определена как квантовая теория поля для произвольно высоких энергий.^[25] Константа связи стремится к бесконечности при конечной энергии, сигнализируя о том, что Полюс Ландау. Проблема в том, что QED, похоже, страдает от квантовая тривиальность вопросы. Это одна из причин встраивания КЭД в Теория Великого Объединения.

Смотрите также

Рекомендации

дальнейшее чтение

Книги

• Де Бройль, Луи (1925). Recherches sur la Theorie des Quanta [Исследования по квантовой теории]. Франция: Wiley-Interscience.
• Фейнман, Ричард Филлипс (1998). Квантовая электродинамика (Новое изд.). Westview Press. ISBN  978-0-201-36075-2.
• Jauch, J.M .; Рорлих, Ф. (1980). Теория фотонов и электронов. Springer-Verlag. ISBN  978-0-387-07295-1.
• Грейнер, Уолтер; Bromley, D.A .; Мюллер, Берндт (2000). Калибровочная теория слабых взаимодействий. Springer. ISBN  978-3-540-67672-0.
• Кейн, Гордон, Л. (1993). Современная физика элементарных частиц. Westview Press. ISBN  978-0-201-62460-1.
• Миллер, Артур I. (1995). Ранняя квантовая электродинамика: справочник. Издательство Кембриджского университета. ISBN  978-0-521-56891-3.
• Милонни, Питер В. (1994). Квантовый вакуум: введение в квантовую электродинамику. Бостон: Academic Press. ISBN  0124980805. LCCN  93029780. OCLC  422797902.
• Швебер, Сильван С. (1994). QED и люди, которые это сделали. Издательство Принстонского университета. ISBN  978-0-691-03327-3.
• Швингер, Джулиан (1958). Избранные статьи по квантовой электродинамике. Dover Publications. ISBN  978-0-486-60444-2.
• Таннуджи-Коэн, Клод; Дюпон-Рок, Жак; Гринберг, Гилберт (1997). Фотоны и атомы: введение в квантовую электродинамику. Wiley-Interscience. ISBN  978-0-471-18433-1.

Журналы

• Дадли, J.M .; Кван, А. (1996). «Популярные лекции Ричарда Фейнмана по квантовой электродинамике: Лекции Робба 1979 года в Оклендском университете». Американский журнал физики. 64 (6): 694–98. Bibcode:1996AmJPh..64..694D. Дои:10.1119/1.18234.

внешняя ссылка

• Лекция Фейнмана о вручении Нобелевской премии с описанием эволюции QED и его роли в ней
• Лекции Фейнмана в Новой Зеландии по КЭД для нефизиков
• http://qed.wikina.org/ - Анимации, демонстрирующие QED