Когерентность (физика) - Coherence (physics)

В физика, два источника волн идеально когерентны, если их частота и форма волны идентичны и их разность фаз постоянно. Когерентность - идеальное свойство волны что обеспечивает стационарность (т.е. постоянство во времени и пространстве) вмешательство. Он содержит несколько различных концепций, которые представляют собой предельные случаи, которые никогда не встречаются в реальности, но позволяют понять физику волн, и стали очень важной концепцией в квантовой физике. В более общем смысле, согласованность описывает все свойства корреляция между физические величины одной волны или между несколькими волнами или волновыми пакетами.

Интерференция - это сложение в математическом смысле волновых функций. Одна волна может интерферировать сама с собой, но это все же сложение двух волн (см. Щели эксперимент Юнга ). Конструктивные или деструктивные интерференции являются предельными случаями, и две волны всегда интерферируют, даже если результат сложения сложен или незначителен. При возникновении помех две волны могут складываться вместе, чтобы создать волну большей амплитуды, чем одна (конструктивное вмешательство ) или вычесть друг из друга, чтобы создать волну меньшей амплитуды, чем любой из них (деструктивное вмешательство ), в зависимости от их родственников фаза. Две волны называются когерентными, если они имеют постоянную относительную фазу. Степень согласованности легко измерить с помощью видимость помех, который учитывает размер интерференционных полос относительно входных волн (при изменении сдвига фазы); точное математическое определение степень согласованности задается с помощью корреляционных функций.

Пространственная когерентность описывает корреляцию (или предсказуемую взаимосвязь) между волнами в разных точках пространства, как поперечных, так и продольных.^[1] Временная когерентность описывает корреляцию между волнами, наблюдаемыми в разные моменты времени. Оба наблюдаются в Эксперимент Майкельсона-Морли и Интерференционный эксперимент Юнга. Как только бахрома получена в Интерферометр Майкельсона, когда одно из зеркал постепенно отодвигается, время прохождения луча увеличивается, полосы становятся тусклыми и, наконец, исчезают, показывая временную когерентность. Аналогично, если в двухщелевой эксперимент, пространство между двумя щелями увеличивается, когерентность постепенно исчезает, и, наконец, полосы исчезают, показывая пространственную когерентность. В обоих случаях амплитуда полос медленно исчезает, поскольку разность хода увеличивается, превышая длину когерентности.

Вступление

Первоначально когерентность была задумана в связи с Томас Янг с двухщелевой эксперимент в оптика но теперь используется в любой области, связанной с волнами, например акустика, электротехника, нейробиология, и квантовая механика. Когерентность описывает статистическое подобие поля (электромагнитного поля, квантового волнового пакета и т. Д.) В двух точках пространства или времени.^[2] Свойство согласованности лежит в основе коммерческих приложений, таких как голография, то Саньяк гироскоп, радио антенные решетки, оптической когерентной томографии и телескопические интерферометры (астрономические оптические интерферометры и радиотелескопы ).

Математическое определение

Точное определение дано в степень согласованности.

Функция когерентности между двумя сигналами ${ Displaystyle х (т)}$ и ${ Displaystyle у (т)}$ определяется как^[3]

${ displaystyle gamma _ {xy} ^ {2} (f) = { frac {| S_ {xy} (f) | ^ {2}} {S_ {xx} (f) S_ {yy} (f) }}}$

куда ${ displaystyle S_ {xy} (е)}$ это кросс-спектральная плотность сигнала и ${ Displaystyle S_ {хх} (е)}$ и ${ displaystyle S_ {yy} (е)}$ сила спектральная плотность функции ${ Displaystyle х (т)}$ и ${ Displaystyle у (т)}$, соответственно. Кросс-спектральная плотность и спектральная плотность мощности определяются как Преобразования Фурье из взаимная корреляция и автокорреляция сигналы соответственно. Например, если сигналы являются функциями времени, взаимная корреляция - это мера сходства двух сигналов как функция временного запаздывания относительно друг друга, а автокорреляция - это мера сходства каждого сигнала с самим собой. в разные моменты времени. В этом случае когерентность является функцией частоты. Аналогично, если ${ Displaystyle х (т)}$ и ${ Displaystyle у (т)}$ являются функциями пространства, взаимная корреляция измеряет подобие двух сигналов в разных точках пространства, а автокорреляция - сходство сигнала относительно самого себя на определенном расстоянии разнесения. В этом случае согласованность является функцией волновое число (пространственная частота).

Когерентность меняется в интервале ${ displaystyle 0 leqslant gamma _ {xy} ^ {2} (f) leqslant 1.}$. Если ${ Displaystyle гамма _ {ху} ^ {2} (е) = 1}$ это означает, что сигналы идеально коррелированы или линейно связаны, и если ${ Displaystyle гамма _ {ху} ^ {2} (е) = 0}$ они совершенно не коррелированы. Если измеряется линейная система, ${ Displaystyle х (т)}$ вход и ${ Displaystyle у (т)}$ на выходе функция когерентности будет унитарной по всему спектру. Однако, если в системе присутствуют нелинейности, когерентность будет изменяться в указанном выше пределе.

Согласованность и корреляция

Когерентность двух волн выражает, насколько хорошо коррелированы волны, что определяется количественно взаимная корреляция функция.^{[4][5][6][7][8]} Взаимная корреляция количественно определяет способность предсказывать фазу второй волны, зная фазу первой. В качестве примера рассмотрим две волны, идеально коррелированные на все времена. В любой момент разность фаз будет постоянной.^{[требуется разъяснение ]} Если при объединении они демонстрируют идеальную конструктивную интерференцию, совершенную деструктивную интерференцию или что-то среднее, но с постоянной разностью фаз, то из этого следует, что они совершенно когерентны. Как будет показано ниже, вторая волна не обязательно должна быть отдельной сущностью. Это может быть первая волна в другое время или в другом месте. В этом случае мерой корреляции является автокорреляция функция (иногда называемая самосогласованность). Степень корреляции включает корреляционные функции.^[9]:545-550

Примеры волновых состояний

Эти состояния объединяет то, что их поведение описывается волновое уравнение или какое-то его обобщение.

• Волны в канате (вверх и вниз) или обтягивающий (сжатие и расширение)
• Поверхностные волны в жидкости
• Электромагнитный сигналы (поля) в линии передачи
• Звук
• Радиоволны и Микроволны
• Световые волны (оптика )
• Электроны, атомы и любой другой объект (например, бейсбольный мяч), как описано квантовая физика

В большинстве этих систем можно напрямую измерить волну. Следовательно, его корреляцию с другой волной можно просто рассчитать. Однако в оптике нельзя измерить электрическое поле напрямую, поскольку он колеблется намного быстрее, чем разрешение любого детектора.^[10] Вместо этого измеряется интенсивность света. Большинство концепций, связанных с когерентностью, которые будут представлены ниже, были разработаны в области оптики, а затем использовались в других областях. Следовательно, многие стандартные измерения когерентности являются косвенными измерениями даже в тех областях, где волна может быть измерена напрямую.

Временная согласованность

Рисунок 1: Амплитуда одночастотной волны как функция времени т (красный) и копия той же волны, задержанная на τ (синий). Время когерентности волны бесконечно, поскольку она идеально коррелирует сама с собой для всех задержек τ.^[11]:118

Рисунок 2: Амплитуда волны, фаза которой существенно меняется во времени τ_c как функция времени т (красный) и копия той же волны с задержкой на 2τ_c(зеленый). В любой момент времени t волна может идеально интерферировать со своей отложенной копией. Но поскольку половину времени красные и зеленые волны находятся в фазе, а половину времени - вне фазы, при усреднении по t любые помехи исчезают на этой задержке.

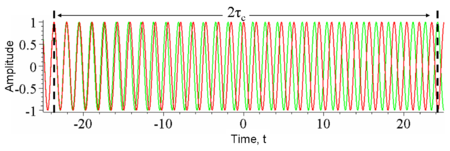
Временная когерентность - это мера средней корреляции между значением волны и самой волной, задержанной на τ, в любую пару моментов времени. Временная согласованность говорит нам о монохроматичности источника. Другими словами, он характеризует, насколько хорошо волна может интерферировать сама с собой в разное время. Задержка, при которой фаза или амплитуда значительно отклоняется (и, следовательно, корреляция значительно уменьшается), определяется как время согласованности τ_c. При задержке τ = 0 степень когерентности идеальная, тогда как она значительно падает по мере прохождения задержки. τ = τ_c. В длина когерентности L_c определяется как расстояние, которое проходит волна за время τ_c.^{[9]:560, 571–573}

Следует соблюдать осторожность, чтобы не путать время когерентности с длительностью сигнала, а также длину когерентности с площадью когерентности (см. Ниже).

Связь между временем когерентности и пропускной способностью

Можно показать, что чем больше диапазон частот Δf содержит волна, тем быстрее волна декоррелирует (и, следовательно, тем меньше τ_c является). Таким образом, существует компромисс:^{[9]:358-359, 560}

${ displaystyle tau _ {c} Delta f gtrsim 1}$.

Формально это следует из теорема свертки в математике, которая связывает преобразование Фурье спектра мощности (интенсивности каждой частоты) к ее автокорреляция.^[9]:572

Примеры временной согласованности

Мы рассматриваем четыре примера временной когерентности.

• Волна, содержащая только одну частоту (монохроматическую), идеально коррелирует сама с собой при всех временных задержках в соответствии с указанным выше соотношением. (См. Рисунок 1)
• И наоборот, волна с быстрым дрейфом фазы будет иметь короткое время когерентности. (См. Рисунок 2)
• Аналогично импульсы (волновые пакеты ) волн, которые, естественно, имеют широкий диапазон частот, также имеют короткое время когерентности, поскольку амплитуда волны изменяется быстро. (См. Рисунок 3)
• Наконец, белый свет, который имеет очень широкий диапазон частот, представляет собой волну, которая быстро изменяется как по амплитуде, так и по фазе. Поскольку, следовательно, он имеет очень короткое время когерентности (всего 10 периодов или около того), его часто называют некогерентным.

Монохроматические источники обычно лазеры; такая высокая монохроматичность подразумевает большие длины когерентности (до сотен метров). Например, стабилизированный и мономодовый гелий-неоновый лазер может легко производить свет с длиной когерентности 300 м.^[12] Однако не все лазеры являются монохроматическими (например, для лазеров с синхронизацией мод. Ti-сапфировый лазер, Δλ ≈ 2 нм - 70 нм). Светодиоды характеризуются Δλ ≈ 50 нм, а лампы с вольфрамовой нитью - Δλ ≈ 600 нм, поэтому эти источники имеют более короткое время когерентности, чем большинство монохроматических лазеров.

Голография требует света с большим временем когерентности. В отличие, оптической когерентной томографии в классическом варианте использует свет с коротким временем когерентности.

Измерение временной когерентности

Рисунок 3: Амплитуда волнового пакета, амплитуда которого существенно изменяется во времени τ_c (красный) и копия той же волны с задержкой на 2τ_c(зеленый) график как функция времени т. В любой конкретный момент красная и зеленая волны не коррелируют; один колеблется, а другой - постоянен, поэтому при этой задержке не будет никаких помех. Другой способ взглянуть на это - волновые пакеты не перекрываются во времени, и поэтому в любой конкретный момент времени существует только одно ненулевое поле, поэтому интерференция не может возникнуть.

Рисунок 4: Усредненная по времени интенсивность (синий цвет), обнаруженная на выходе интерферометра, построенная как функция задержки τ для примеров волн на рисунках 2 и 3. При изменении задержки на половину периода интерференция переключается между конструктивными и разрушительный. Черные линии указывают на интерференционную огибающую, которая дает степень согласованности. Хотя волны на рисунках 2 и 3 имеют разную длительность, у них одинаковое время когерентности.

В оптике временная когерентность измеряется с помощью интерферометра, такого как Интерферометр Майкельсона или же Интерферометр Маха – Цендера. В этих устройствах волна совмещается с собственной копией, задержанной на время τ. Детектор измеряет усредненное по времени интенсивность света, выходящего из интерферометра. Результирующая видимость помех (например, см. Рисунок 4) дает временную когерентность при задержке τ. Поскольку для большинства естественных источников света время когерентности намного короче временного разрешения любого детектора, детектор сам производит усреднение по времени. Рассмотрим пример, показанный на рисунке 3. При фиксированной задержке здесь 2τ_c, бесконечно быстрый детектор будет измерять интенсивность, которая значительно колеблется во времени т равно τ_c. В этом случае для нахождения временной когерентности при 2τ_c, можно было бы вручную усреднить интенсивность по времени.

Пространственная согласованность

В некоторых системах, таких как водные волны или оптика, волновые состояния могут распространяться на одно или два измерения. Пространственная согласованность описывает способность двух точек в пространстве, Икс₁ и Икс₂, в степени интерферирующей волны при усреднении по времени. Точнее, пространственная когерентность - это взаимная корреляция между двумя точками в волне на все времена. Если волна имеет только одно значение амплитуды на бесконечной длине, она идеально пространственно когерентна. Диапазон разноса между двумя точками, в котором наблюдается значительная интерференция, определяет диаметр области когерентности, А_c^[13] (Длина когерентности, часто являющаяся характеристикой источника, обычно является промышленным термином, связанным со временем когерентности источника, а не площадью когерентности в среде.)_c является подходящим типом когерентности для двухщелевого интерферометра Юнга. Он также используется в оптических системах формирования изображений и, в частности, в различных типах астрономических телескопов. Иногда люди также используют «пространственную когерентность» для обозначения видимости, когда волнообразное состояние сочетается с пространственно смещенной копией самого себя.

Примеры

• Пространственная согласованность
• 

  Рисунок 5: Плоская волна с бесконечной длина когерентности.

• 

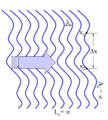
  Рисунок 6: Волна с переменным профилем (волновым фронтом) и бесконечной длиной когерентности.

• 

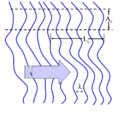
  Рисунок 7: Волна с переменным профилем (волновым фронтом) и конечной длиной когерентности.

• 

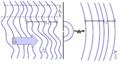
  Рис. 8: Волна с конечной площадью когерентности падает на точечное отверстие (маленькое отверстие). Волна будет преломлять из отверстия. Вдали от отверстия возникающие сферические волновые фронты примерно плоские. Область когерентности теперь бесконечна, а длина когерентности не изменилась.

• 

  Рисунок 9: Волна с бесконечной областью когерентности сочетается с пространственно смещенной копией самой себя. Некоторые участки в волне создают интерференцию конструктивно, а некоторые деструктивную. Усредняя по этим участкам, детектор длиной D будет измерять уменьшенные видимость помех. Например, смещенный Интерферометр Маха – Цендера сделаю это.

Рассмотрим нить накаливания вольфрамовой лампочки. Различные точки нити накала излучают свет независимо и не имеют фиксированного фазового соотношения. В частности, в любой момент времени профиль излучаемого света будет искажен. Профиль будет случайным образом меняться в течение времени согласования. ${ displaystyle tau _ {c}}$. Поскольку для источника белого света, такого как лампочка ${ displaystyle tau _ {c}}$ мала, нить считается пространственно некогерентным источником. Напротив, радио антенная решетка, имеет большую пространственную когерентность, потому что антенны на противоположных концах решетки излучают с фиксированным фазовым соотношением. Световые волны, создаваемые лазером, часто имеют высокую временную и пространственную когерентность (хотя степень когерентности сильно зависит от точных свойств лазера). Пространственная когерентность лазерных лучей также проявляется в виде спекл-структур и дифракционных полос по краям тени.

Голография требует когерентного во времени и пространстве света. Его изобретатель, Деннис Габор, произвела успешные голограммы более чем за десять лет до изобретения лазеров. Чтобы произвести когерентный свет, он пропустил монохроматический свет от линии излучения ртутная лампа через пространственный фильтр с отверстиями.

В феврале 2011 года сообщалось, что гелий атомы, охлажденные почти до абсолютный ноль / Конденсат Бозе – Эйнштейна состояние, можно заставить течь и вести себя как когерентный луч, как в лазере.^[14][15]

Спектральная когерентность

Рисунок 10: Волны разных частот мешают формировать локализованный импульс, если они когерентны.

Рисунок 11: Спектрально некогерентный свет мешает формировать непрерывный свет со случайным образом изменяющейся фазой и амплитудой.

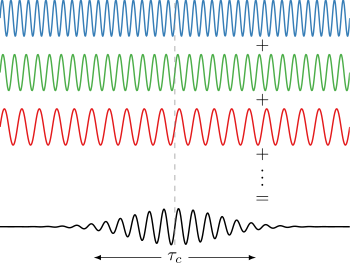
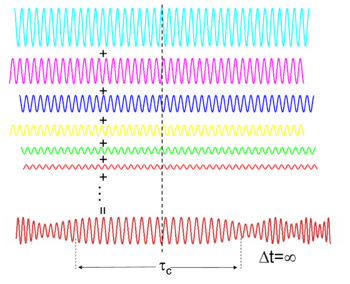
Волны разной частоты (в свете это разные цвета) могут мешать формированию импульса, если они имеют фиксированное относительное фазовое соотношение (см. преобразование Фурье ). И наоборот, если волны разных частот не когерентны, то при объединении они создают непрерывную во времени волну (например, белый свет или белый шум ). Временная длительность пульса ${ displaystyle Delta t}$ ограничен спектральной полосой света ${ displaystyle Delta f}$ в соответствии с:

${ displaystyle Delta f Delta t geq 1}$,

что следует из свойств преобразования Фурье и приводит к Принцип неопределенности Купфмюллера (для квантовых частиц это также приводит к Принцип неопределенности Гейзенберга ).

Если фаза линейно зависит от частоты (т.е. ${ displaystyle theta (f) propto f}$), то импульс будет иметь минимальную временную длительность для своей полосы пропускания (a ограниченный трансформацией импульс), в противном случае он будет чирпироваться (см. разброс ).

Измерение спектральной когерентности

Для измерения спектральной когерентности света требуется нелинейный оптический интерферометр, такой как интенсивность оптический коррелятор, оптический строб с частотным разрешением (FROG), или спектральная фазовая интерферометрия для прямой реконструкции электрического поля (ПАУК).

Поляризация и когерентность

Свет также имеет поляризация, которое является направлением колебаний электрического поля. Неполяризованный свет состоит из некогерентных световых волн со случайными углами поляризации. Электрическое поле неполяризованного света блуждает во всех направлениях и изменяется по фазе за время когерентности двух световых волн. Увлекательный поляризатор повернутый на любой угол всегда будет передавать половину падающей интенсивности при усреднении по времени.

Если электрическое поле отклоняется на меньшую величину, свет будет частично поляризован, так что под некоторым углом поляризатор будет пропускать более половины интенсивности. Если волна комбинируется с ортогонально поляризованной копией самой себя, задержанной меньше, чем время когерентности, создается частично поляризованный свет.

Поляризация светового луча представлена ​​вектором в Сфера Пуанкаре. Для поляризованного света конец вектора лежит на поверхности сферы, в то время как вектор имеет нулевую длину для неполяризованного света. Вектор частично поляризованного света лежит внутри сферы

Приложения

Голография

Когерентные суперпозиции поля оптических волн включают голография. Голографические объекты часто используются в повседневной жизни на телевидении и в защите кредитных карт.

Неоптические волновые поля

Дальнейшие приложения касаются когерентной суперпозиции неоптические волновые поля. В квантовой механике, например, рассматривается поле вероятностей, которое связано с волновой функцией ${ displaystyle psi ( mathbf {r})}$ (интерпретация: плотность амплитуды вероятности). Здесь приложения касаются, в частности, будущих технологий квантовые вычисления и уже доступная технология квантовая криптография. Дополнительно рассматриваются проблемы следующего подраздела.

Модальный анализ

Когерентность используется для проверки качества измеряемых передаточных функций (FRF). Низкая когерентность может быть вызвана плохим соотношением сигнал / шум и / или неадекватным разрешением по частоте.

Квантовая когерентность

Эта секция нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. (Декабрь 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

В квантовая механика, все объекты имеют волнообразные свойства (см. волны де Бройля ). Например, в книге Янга двухщелевой эксперимент электроны можно использовать вместо световых волн. Волновая функция каждого электрона проходит через обе щели и, следовательно, имеет два отдельных разделенных луча, которые вносят вклад в картину интенсивности на экране. Согласно стандартной волновой теории^[16] эти два вклада создают картину интенсивности ярких полос из-за конструктивной интерференции, чередующихся с темными полосами из-за деструктивной интерференции, на экране ниже по потоку. Эта способность к интерференции и дифракции связана с когерентностью (классической или квантовой) волн, создаваемых на обеих щелях. Связь электрона с волной уникальна для квантовой теории.

Когда падающий луч представлен квантовой чистое состояние, разделенные балки после двух щелей представлены в виде суперпозиция чистых состояний, представляющих каждый расщепленный пучок.^[17] Квантовое описание несовершенно когерентных путей называется смешанное состояние. Совершенно когерентное состояние имеет матрица плотности (также называемый «статистическим оператором»), который является проекцией на чистое когерентное состояние и эквивалентен волновой функции, в то время как смешанное состояние описывается классическим распределением вероятностей для чистых состояний, составляющих смесь.

Макроскопический масштаб квантовая когерентность приводит к новым явлениям, так называемым макроскопические квантовые явления. Например, лазер, сверхпроводимость и сверхтекучесть являются примерами высокогерентных квантовых систем, эффекты которых очевидны на макроскопическом уровне. Макроскопическая квантовая когерентность (недиагональный дальний порядок, ODLRO)^[18][19] для сверхтекучести и лазерного света связана с когерентностью первого порядка (1-тела) / ODLRO, а сверхпроводимость связана с когерентностью второго порядка / ODLRO. (Для фермионов, таких как электроны, возможны только четные порядки когерентности / ODLRO.) Для бозонов a Конденсат Бозе – Эйнштейна является примером системы, демонстрирующей макроскопическую квантовую когерентность через многократно занятое одночастичное состояние.

Классическое электромагнитное поле демонстрирует макроскопическую квантовую когерентность. Самый очевидный пример - несущий сигнал для радио и телевидения. Они удовлетворяют Глаубер квантовое описание когерентности.

Недавно М. Б. Пленио и его сотрудники построили операциональную формулировку квантовой когерентности как теории ресурсов. Они ввели монотоны когерентности, аналогичные монотонам сцепленности.^[20] Было показано, что квантовая когерентность эквивалентна квантовая запутанность^[21] в том смысле, что когерентность можно точно описать как запутанность, и наоборот, что каждая мера запутанности соответствует мере когерентности.

Смотрите также

Рекомендации

внешняя ссылка

• Доктор SkySkull (3 сентября 2008 г.). «Основы оптики: когерентность». Черепа в звездах.