Источник одиночных фотонов на квантовых точках - Википедия - Quantum dot single-photon source
А однофотонный источник квантовых точек основан на едином квантовая точка помещен в оптический резонатор. Это источник однофотонов по запросу. Лазерный импульс может возбудить пару носителей, известную как экситон в квантовой точке. Распад одиночного экситона за счет спонтанное излучение приводит к испусканию одиночного фотона. Из-за взаимодействий между экситонами излучение, когда квантовая точка содержит один экситон, энергетически отличается от излучения, когда квантовая точка содержит более одного экситона. Следовательно, одиночный экситон может быть детерминированно создан лазерным импульсом, и квантовая точка становится неклассический свет источник, который излучает фотоны один за другим и таким образом показывает антигруппировка фотонов. Эмиссия одиночных фотонов может быть подтверждена измерением корреляционная функция интенсивности второго порядка. В спонтанное излучение ставка выпущенного фотоны можно улучшить, интегрировав квантовую точку в оптический резонатор. Кроме того, резонатор приводит к излучению в четко определенной оптической моде, повышая эффективность источника фотонов.
История
С ростом интереса к квантовая информатика С начала XXI века исследования в области однофотонных источников разного типа росли. Ранние однофотонные источники, такие как известные источники фотонов[1] о которых впервые было сообщено в 1985 году, основаны на недетерминированных процессах. Источники однофотонных квантовых точек доступны по запросу. Об источнике однофотонов на основе квантовой точки в структуре микродиска было сообщено в 2000 году.[2] Источники впоследствии были встроены в различные структуры, такие как фотонные кристаллы.[3] или микростолпы.[4] Добавление DBR позволило излучение в четко определенном направлении и повысило эффективность излучения.[5] Большинство источников однофотонных квантовых точек должны работать на криогенные температуры, что по-прежнему является технической проблемой.[5] Другой проблемой является реализация высококачественных источников однофотонных квантовых точек на длине волны связи для применения в волоконной электросвязи.[6] В первом отчете об усиленном Парселлом однофотонном излучении квантовой точки с длиной волны телекоммуникационного излучения в двумерном фотонно-кристаллическом резонаторе с добротностью 2000 показано увеличение скорости излучения и интенсивности в пять и шесть раз соответственно.[7]
Теория реализации однофотонного источника
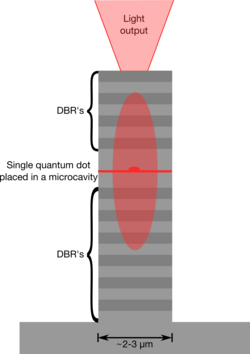
Возбуждая электрон в полупроводник от валентная полоса к зона проводимости создает возбужденное состояние, так называемое экситон. Спонтанный радиационный распад этого экситона приводит к испусканию фотона. Поскольку квантовая точка имеет дискретные уровни энергии, можно добиться, чтобы в квантовой точке одновременно не было более одного экситона. Следовательно, квантовая точка является излучателем одиночных фотонов. Ключевой задачей при создании хорошего однофотонного источника является обеспечение эффективного улавливания излучения квантовой точки. Для этого квантовую точку помещают в оптический резонатор. Полость может, например, состоять из двух РБО в микропилларе (рис. 1). Резонатор усиливает спонтанное излучение в четко определенной оптической моде (Эффект Перселла ), способствуя эффективному направлению излучения в оптическое волокно. Кроме того, уменьшенное время жизни экситона (см. рис. 2) снижает значимость уширение линии из-за шума.

Тогда система может быть аппроксимирована Модель Джейнса-Каммингса. В этой модели квантовая точка взаимодействует только с одной модой оптического резонатора. Частота оптической моды хорошо определена. Это делает фотоны неразличимыми, если их поляризация выровнен поляризатор. Решением гамильтониана Джейнса-Каммингса является вакуумное колебание Раби. Вакуумные колебания Раби фотона, взаимодействующего с экситоном, известны как экситон-поляритон.
Чтобы исключить вероятность одновременного излучения двух фотонов, необходимо убедиться, что в резонаторе одновременно может находиться только один экситон. Дискретные энергетические состояния в квантовой точке допускают только одно возбуждение. Кроме того, блокада Ридберга предотвращает возбуждение двух экситонов в одном и том же пространстве ...[8] В электромагнитное взаимодействие с уже существующим экситоном заметно меняет энергию для создания другого экситона в том же пространстве. Если энергия лазера накачки настроена на резонанс, второй экситон не может быть создан, но есть небольшая вероятность одновременного появления двух возбуждений в квантовой точке. Два экситона, заключенные в малый объем, называются биэкситоны. Они взаимодействуют друг с другом и, таким образом, немного меняют свою энергию. Фотоны, возникающие при распаде биэкситонов, имеют энергию, отличную от энергии фотонов, возникающих при распаде экситонов. Их можно отфильтровать, пропустив выходящий луч через оптический фильтр.[9] Квантовые точки можно возбуждать как электрически, так и оптически.[5] Для оптической накачки используется импульсный лазер можно использовать для возбуждения квантовых точек. Чтобы иметь максимальную вероятность создания экситона, лазер накачки настроен на резонанс.[10] Это похоже на -импульс на Сфера Блоха. Однако в этом случае излучаемые фотоны имеют ту же частоту, что и лазер накачки. Чтобы различать их, необходим поляризатор.[10] Поскольку направление поляризации фотонов из полости случайное, половина излучаемых фотонов блокируется этим фильтром.
Экспериментальная реализация
Создан микрополость с одной квантовой точкой. DBR могут быть увеличены молекулярно-лучевая эпитаксия (MBE). Для зеркал два материала с разными показатели преломления выращиваются в альтернативном порядке. Их параметры решетки должны совпадать во избежание деформации. Возможная комбинация - это комбинация арсенид алюминия и арсенид галлия -слои.[10] Материал с меньшим запрещенная зона используется для выращивания квантовой точки. В первых нескольких атомных слоях выращивания этого материала постоянная решетки будет соответствовать постоянной решетки РБО. Появляется деформация растяжения. При определенной толщине энергия деформации становится слишком большой, и слой сжимается, чтобы расти со своей постоянной решеткой. На данный момент квантовые точки сформировались естественным образом. Второй слой РБО теперь можно выращивать поверх слоя с квантовыми точками.
Диаметр столба составляет всего несколько микрон. Чтобы предотвратить выход оптической моды из резонатора, микростолбик должен действовать как волновод. Полупроводники обычно имеют относительно высокий показатель преломления около nÀ3.[11]Следовательно, их конус извлечения небольшой. На гладкой поверхности микростолбик работает как почти идеальный волновод. Однако потери увеличиваются с шероховатостью стенок и уменьшением диаметра микростолба.[12]
Таким образом, края должны быть как можно более гладкими, чтобы минимизировать потери. Этого можно достичь, структурируя образец с помощью Электронно-лучевая литография и обработка столбов реактивное ионное травление.[9]
Проверка излучения одиночных фотонов
Источники одиночных фотонов демонстрируют антигруппирование. Поскольку фотоны излучаются по одному, вероятность увидеть два фотона одновременно для идеального источника равна 0. Чтобы проверить антигруппировку источника света, можно измерить автокорреляционную функцию. . Источник фотонов антигруппирован, если ≤ .[13] Для идеального источника одиночных фотонов . Экспериментально измеряется с помощью Эффект Хэнбери Брауна и Твисса. Приборы экспериментально показывают значения между [10] и [14] при криогенных температурах.
Неразличимость испускаемых фотонов
Для приложений фотоны, испускаемые одним источником фотонов, должны быть неотличимый. Теоретическое решение гамильтониана Джейнса-Каммингса представляет собой четко определенный режим, в котором только поляризация является случайной. После совмещения поляризации фотонов можно измерить их неотличимость. Для этого Эффект Хонг-У-Манделя используется. Два фотона источника подготавливаются таким образом, что они попадают в пропорцию 50:50. Разделитель луча одновременно с двух разных входных каналов. А детектор размещен на обоих выходах светоделителя. Измеряются совпадения между двумя детекторами. Если фотоны неразличимы, совпадений быть не должно.[15] Экспериментально обнаруживается почти идеальная неразличимость.[14][10]
Приложения
Однофотонные источники имеют большое значение в квантовой коммуникации. Их можно использовать для генераторов действительно случайных чисел.[5] Одиночные фотоны, попадающие в светоделитель, обладают свойственной квантовая неопределенность. Случайные числа широко используются при моделировании с использованием Метод Монте-Карло.
Кроме того, источники одиночных фотонов необходимы в квантовая криптография. В BB84[16] схема - это доказуемо безопасный квантовое распределение ключей схема. Он работает с источником света, который идеально излучает только один фотон за раз. Из-за теорема о запрете клонирования,[17] ни одно подслушивание не может произойти незамеченным. Использование квантовой случайности при записи ключа предотвращает любые шаблоны в ключе, которые могут использоваться для расшифровки кода.
Кроме того, источники одиночных фотонов можно использовать для проверки некоторых фундаментальных свойств квантовая теория поля.[1]
Смотрите также
Рекомендации
- ^ а б Гранжье, Филипп; Роджер, Джерард; Аспект, Ален (1986). «Экспериментальное доказательство эффекта антикорреляции фотонов на светоделителе: новый свет на однофотонную интерференцию». EPL (Еврофизические письма). 1 (4): 173. Bibcode:1986EL ...... 1..173G. CiteSeerX 10.1.1.178.4356. Дои:10.1209/0295-5075/1/4/004.
- ^ Michler, P .; Кираз, А .; Becher, C .; Schoenfeld, W.V .; Петров П.М.; Чжан, Лидун; Hu, E .; Имамоглу, А. (2000). "Однофотонный турникет на квантовых точках". Наука. 290 (5500): 2282–2285. Bibcode:2000Sci ... 290.2282M. Дои:10.1126 / science.290.5500.2282. PMID 11125136.
- ^ Kress, A .; Hofbauer, F .; Reinelt, N .; Канибер, М .; Krenner, HJ; Meyer, R .; Böhm, G .; Финли, Дж. Дж. (2005). «Манипуляция динамикой спонтанного излучения квантовых точек в двумерных фотонных кристаллах». Phys. Ред. B. 71 (24): 241304. arXiv:Quant-ph / 0501013. Bibcode:2005PhRvB..71x1304K. Дои:10.1103 / PhysRevB.71.241304. S2CID 119442776.
- ^ Moreau, E .; Роберт, I .; Gérard, J.M .; Abram, I .; Манин, Л .; Тьерри-Миг, В. (2001). «Одномодовый твердотельный однофотонный источник на основе изолированных квантовых точек в столбчатых микрополостях». Appl. Phys. Латыш. 79 (18): 2865–2867. Bibcode:2001АпФЛ..79.2865М. Дои:10.1063/1.1415346.
- ^ а б c d Eisaman, M.D .; Fan, J .; Migdall, A .; Поляков, С. В. (01.07.2011). «Приглашенная обзорная статья: источники и детекторы одиночных фотонов». Обзор научных инструментов. 82 (7): 071101–071101–25. Bibcode:2011RScI ... 82g1101E. Дои:10.1063/1.3610677. ISSN 0034-6748. PMID 21806165.
- ^ Senellart, P .; Соломон, G .; Белый, А. (2017). «Высокопроизводительные полупроводниковые источники однофотонных квантовых точек». Природа Нанотехнологии. 12 (11): 1026–1039. Bibcode:2017НатНа..12.1026С. Дои:10.1038 / nnano.2017.218. PMID 29109549.
- ^ Birowosuto, M.D .; Sumikura, H .; Matsuo, S .; Taniyama, H .; Veldhoven, P.J .; Notzel, R .; Нотоми, М. (2012). «Быстрый источник одиночных фотонов с усилением Пёрселла в телекоммуникационном диапазоне 1550 нм за счет резонансной связи квантовой точки и резонатора». Sci. Представитель. 2: 321. arXiv:1203.6171. Bibcode:2012НатСР ... 2Э.321Б. Дои:10.1038 / srep00321. ЧВК 3307054. PMID 22432053.
- ^ Т. Казимерчук; Д. Фрёлих; С. Шил; Х. Штольц и М. Байер (2014). «Гигантские ридберговские экситоны в оксиде меди Cu2O». Природа. 514 (7522): 343–347. arXiv:1407.0691. Bibcode:2014Натура.514..343K. Дои:10.1038 / природа13832. PMID 25318523. S2CID 4470179.
- ^ а б Золото, Питер (2015). "Quantenpunkt-Mikroresonatoren als Bausteine für die Quantenkommunikation". Цитировать журнал требует
| журнал =(помощь) - ^ а б c d е Дин, Син; Эй ты; Дуань, З-Ц; Грегерсен, Нильс; Чен, МС; Анслебер, С; Майер, Себастьян; Шнайдер, Кристиан; Камп, Мартин; Хёфлинг, Свен; Лу, Чао-Ян; Пан, Цзянь-Вэй (2016). «Одиночные фотоны по запросу с высокой эффективностью извлечения и почти единичной неотличимостью от резонансной квантовой точки в микростолпе». Письма с физическими проверками. 116 (2): 020401. arXiv:1507.04937. Bibcode:2016ПхРвЛ.116а0401П. Дои:10.1103 / PhysRevLett.116.010401. PMID 26799002. S2CID 206266974.
- ^ Herve, P .; Вандамм, Л. К. Дж. (1994). «Общая связь между показателем преломления и запрещенной зоной в полупроводниках». Инфракрасная физика и технологии. 35 (4): 609–615. Bibcode:1994ИнФТ..35..609Х. Дои:10.1016/1350-4495(94)90026-4.
- ^ Reitzenstein, S. и Forchel, A. (2010). «Микростолбы из квантовых точек». Журнал физики D: Прикладная физика. 43 (3): 033001. Дои:10.1088/0022-3727/43/3/033001.
- ^ Пол, H (1982). «Антигруппировка фотонов». Обзоры современной физики. 54 (4): 1061–1102. Bibcode:1982РвМП ... 54.1061П. Дои:10.1103 / RevModPhys.54.1061.
- ^ а б Сомаши, Никколо; Гисс, Валериан; Де Сантис, Лоренцо; Лоредо, JC; Алмейда, Марсело П.; Хорнекер, Гастон; Порталупи, Симоне Лука; Грейндж, Томас; Антон, Карлос; Демори, Джастин (2016). «Почти оптимальные источники одиночных фотонов в твердом состоянии». Природа Фотоника. 10 (5): 340–345. arXiv:1510.06499. Bibcode:2016НаФо..10..340С. Дои:10.1038 / nphoton.2016.23. S2CID 119281960.
- ^ К. К. Хонг; З. Ю. Оу и Л. Мандель (1987). «Измерение субпикосекундных интервалов времени между двумя фотонами путем интерференции». Phys. Rev. Lett. 59 (18): 2044–2046. Bibcode:1987PhRvL..59.2044H. Дои:10.1103 / PhysRevLett.59.2044. PMID 10035403.
- ^ К. Х. Беннетт и Г. Брассард. «Квантовая криптография: распределение открытых ключей и подбрасывание монет». В Труды Международной конференции IEEE по компьютерам, системам и обработке сигналов, том 175, стр. 8. Нью-Йорк, 1984. http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf
- ^ Wootters, Уильям; Журек, Войцех (1982). «Один квант нельзя клонировать». Природа. 299 (5886): 802–803. Bibcode:1982Натура.299..802Вт. Дои:10.1038 / 299802a0. S2CID 4339227.







