Электрическое поле - Electric field

Электрическое поле
Воздействие электрического поля. Девушка трогает электростатический генератор, который заряжает ее тело высоким напряжением. Ее волосы, заряженные той же полярностью, отражаются электрическим полем ее головы и выступают из-под ее головы.
Общие символы	E
Единица СИ	вольт на метр (В / м)
В Базовые единицы СИ	мкг⋅с−3⋅A−1
Поведение под преобразование координат	вектор
Производные от другие количества	F / q

Часть цикла статей о
Электромагнетизм
Электричество Магнетизм История Учебники
Электростатика Электрический заряд Закон Кулона Дирижер Плотность заряда Разрешающая способность Электрический дипольный момент Электрическое поле Электрический потенциал Электрический поток  / потенциальная энергия Электростатический разряд Закон Гаусса Индукция Изолятор Плотность поляризации Статичное электричество Трибоэлектричество
Магнитостатика Закон Ампера Закон Био – Савара Закон Гаусса для магнетизма Магнитное поле Магнитный поток Магнитный дипольный момент Магнитная проницаемость Магнитный скалярный потенциал Намагничивание Магнитодвижущая сила Правило правой руки
Электродинамика Закон силы Лоренца Электромагнитная индукция Закон Фарадея Закон Ленца Ток смещения Магнитный векторный потенциал Уравнения Максвелла Электромагнитное поле Электромагнитный импульс Электромагнитное излучение Тензор Максвелла Вектор Пойнтинга Потенциал Льенара – Вихерта Уравнения Ефименко Вихревой ток Уравнения Лондона Математические описания электромагнитного поля
Электрическая сеть Переменный ток Емкость Постоянный ток Электрический ток Электролиз Плотность тока Джоулевое нагревание Электродвижущая сила Импеданс Индуктивность Закон Ома Параллельная схема Сопротивление Резонансные полости Последовательная схема Напряжение Волноводы
Ковариантная формулировка Электромагнитный тензор (тензор энергии-импульса ) Четырехтоковый Электромагнитный четырехпотенциальный
Ученые Ампер Биот Кулон Дэви Эйнштейн Фарадей Физо Гаусс Хевисайд Генри Герц Джоуль Ленц Лоренц Максвелл Ørsted Ом Ричи Savart Певица Тесла Вольта Вебер

An электрическое поле (иногда Электронное поле^[1]) это физическое поле что окружает каждый электрический заряд и оказывает силу на все остальные заряды в поле, либо притягивая, либо отталкивая их.^[2][3] Электрические поля возникают из-за электрических зарядов или изменяющихся во времени магнитные поля. Электрические и магнитные поля являются проявлениями электромагнитная сила, один из четырех фундаментальные силы (или взаимодействия) природы.

Электрические поля важны во многих областях физика, и используются практически в электротехнике. В атомная физика и химия, например, электрическое поле используется для моделирования силы притяжения, удерживающей атомное ядро и электроны вместе в атомах. Он также моделирует силы в химическая связь между атомами, что приводит к молекулы.

Электрическое поле математически определяется как векторное поле который связывает с каждой точкой в ​​пространстве (электростатический или Кулон ) сила на единицу обвинять на бесконечно малое положительное тестовая зарядка в состоянии покоя в этот момент.^[4][5][6] В производная СИ единицы для электрического поля вольт на метр (В / м), что в точности эквивалентно ньютоны на кулон (N / C).^[7]

Описание

Электрическое поле положительной точки электрический заряд подвешен на бесконечном листе проводящего материала. Поле обозначено силовые линии электрического поля, линии, которые следуют направлению электрического поля в пространстве.

Электрическое поле определяется в каждой точке пространства как сила (на единицу заряда), которую испытывает исчезающе маленький положительный тестовая зарядка если держать в этой точке.^[8]:469–70 Поскольку электрическое поле определяется с помощью сила, а сила - это вектор (т.е. имея оба величина и направление ) следует, что электрическое поле векторное поле.^[8]:469–70 Векторные поля этой формы иногда называют силовые поля. Электрическое поле действует между двумя зарядами аналогично тому, как гравитационное поле действует между двумя массы, поскольку они оба подчиняются закон обратных квадратов с расстоянием.^[9] Это основа для Закон Кулона, в котором говорится, что для стационарных зарядов электрическое поле изменяется в зависимости от заряда источника и изменяется обратно пропорционально квадрату расстояния от источника. Это означает, что если бы заряд источника был удвоен, электрическое поле удвоилось бы, а если вы отодвинетесь вдвое дальше от источника, поле в этой точке будет только четверть его первоначальной силы.

Электрическое поле можно визуализировать с помощью набора линии чье направление в каждой точке такое же, как и у поля, концепция введена Майкл Фарадей,^[10] чей срок 'силовые линии 'до сих пор иногда используется. Эта иллюстрация обладает тем полезным свойством, что напряженность поля пропорциональна плотности линий.^[11] Линии поля - это пути, по которым точечный положительный заряд будет следовать, когда он вынужден перемещаться в пределах поля, как и траектории что массы следуют в гравитационном поле. Силовые линии из-за стационарных зарядов имеют несколько важных свойств, в том числе всегда исходят от положительных зарядов и заканчиваются отрицательными зарядами, они входят во все хорошие проводники под прямым углом, и они никогда не пересекаются и не замыкаются между собой.^[8]:479 Линии поля представляют собой репрезентативную концепцию; поле фактически пронизывает все пространство между линиями. Может быть нарисовано больше или меньше линий в зависимости от точности, с которой желательно представить поле.^[10] Исследование электрических полей, создаваемых стационарными зарядами, называется электростатика.

Закон Фарадея описывает связь между изменяющимся во времени магнитным полем и электрическим полем. Один из способов сформулировать закон Фарадея состоит в том, что завиток электрического поля равно отрицательному производная по времени магнитного поля.^[12]:327 Поэтому в отсутствие изменяющегося во времени магнитного поля электрическое поле называется консервативный (т.е. без завитков).^{[12]:24,90–91} Это означает, что есть два вида электрических полей: электростатические поля и поля, возникающие из изменяющихся во времени магнитных полей.^{[12]:305–307} В то время как отсутствие завитков статического электрического поля позволяет упростить лечение с использованием электростатики, изменяющиеся во времени магнитные поля обычно рассматриваются как компонент единого электромагнитное поле. Изучение изменяющихся во времени магнитных и электрических полей называется электродинамика.

Математическая формулировка

Электрические поля вызваны электрические заряды, описанный Закон Гаусса,^[13] и время меняющееся магнитные поля, описанный Закон индукции Фарадея.^[14] Вместе этих законов достаточно, чтобы определить поведение электрического поля. Однако, поскольку магнитное поле описывается как функция электрического поля, уравнения обоих полей связаны и вместе образуют Уравнения Максвелла которые описывают оба поля как функцию зарядов и токи.

Электростатика

В частном случае устойчивое состояние (стационарные заряды и токи) индуктивный эффект Максвелла-Фарадея исчезает. Полученные два уравнения (закон Гаусса ${displaystyle abla cdot mathbf {E} = {frac {ho} {varepsilon _ {0}}}}$ и закон Фарадея без индукционного члена ${displaystyle abla imes mathbf {E} = 0}$), вместе взятые, эквивалентны Закон Кулона, который утверждает, что частица с электрическим зарядом ${displaystyle q_ {1}}$ на позиции ${displaystyle {oldsymbol {x}} _ {1}}$ оказывает силу на частицу с зарядом ${displaystyle q_ {0}}$ на позиции ${displaystyle {oldsymbol {x}} _ {0}}$ из:^[15]

${displaystyle {oldsymbol {F}} = {1 over 4pi varepsilon _ {0}} {q_ {1} q_ {0} over ({oldsymbol {x}} _ {1} - {oldsymbol {x}} _ {0 }) ^ {2}} {hat {oldsymbol {r}}} _ {1,0}}$

куда ${displaystyle {oldsymbol {r}} _ {1,0}}$ это единичный вектор в направлении от точки ${displaystyle {oldsymbol {x}} _ {1}}$ В точку ${displaystyle {oldsymbol {x}} _ {0}}$, и ε₀ это электрическая постоянная (также известная как «абсолютная диэлектрическая проницаемость свободного пространства») с единицами измерения C² м⁻² N⁻¹

Обратите внимание, что ${displaystyle varepsilon _ {0}}$, то электрическая проницаемость вакуума, необходимо заменить на ${displaystyle varepsilon}$, диэлектрическая проницаемость, когда начисления находятся на непустом носителе. ${displaystyle q_ {0}}$ и ${displaystyle q_ {1}}$ имеют тот же знак, что эта сила положительна, направлена ​​в сторону от другого заряда, указывая на то, что частицы отталкиваются друг от друга. Когда заряды имеют разные знаки, сила отрицательна, что указывает на притяжение частиц. Кулоновская сила на любую плату на позиции ${displaystyle {oldsymbol {x}} _ {0}}$ это выражение можно разделить на ${displaystyle q_ {0}}$ оставив выражение, которое зависит только от другого заряда ( источник обвинять)^[16][6]

${displaystyle {oldsymbol {E}} ({oldsymbol {x}} _ {0}) = {{oldsymbol {F}} over q_ {0}} = {1 over 4pi varepsilon _ {0}} {q_ {1}) над ({oldsymbol {x}} _ {1} - {oldsymbol {x}} _ {0}) ^ {2}} {hat {oldsymbol {r}}} _ {1,0}}$

Это электрическое поле в точке ${displaystyle {oldsymbol {x}} _ {0}}$ из-за точечной оплаты ${displaystyle q_ {1}}$; это вектор-функция равной кулоновской силе на единицу заряда, которую положительный точечный заряд испытал бы в положении ${displaystyle {oldsymbol {x}} _ {0}}$Так как эта формула дает величину и направление электрического поля в любой точке ${displaystyle {oldsymbol {x}} _ {0}}$ в космосе (кроме места нахождения самого заряда, ${displaystyle {oldsymbol {x}} _ {1}}$, где он становится бесконечным) он определяет векторное поле Из приведенной выше формулы видно, что электрическое поле, создаваемое точечным зарядом, везде направлено от заряда, если он положительный, и в сторону заряда, если он отрицательный, и его величина уменьшается с увеличением обратный квадрат расстояния от заряда.

Кулоновская сила на заряде величины ${displaystyle q}$ в любой точке пространства равно произведению заряда и электрического поля в этой точке

${displaystyle {oldsymbol {F}} = q {oldsymbol {E}}}$

Единицы электрического поля в SI система ньютоны на кулон (N / C), или вольт на метр (В / м); с точки зрения Базовые единицы СИ они килограммы⁻³⋅A⁻¹

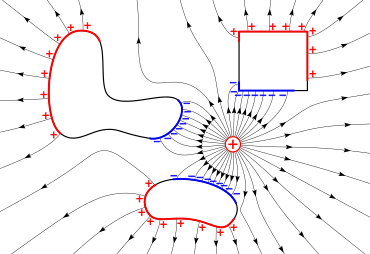
Принцип суперпозиции

Из-за линейность из Уравнения Максвелла, электрические поля удовлетворяют принцип суперпозиции, который утверждает, что полное электрическое поле в точке, обусловленное совокупностью зарядов, равно векторной сумме электрических полей в этой точке, обусловленных отдельными зарядами.^[6] Этот принцип полезен при расчете поля, создаваемого множественными точечными зарядами. Если обвинения ${displaystyle q_ {1}, q_ {2}, ..., q_ {n}}$ неподвижны в пространстве в точках ${displaystyle mathbf {x} _ {1}, mathbf {x} _ {2}, ... mathbf {x} _ {n}}$, в отсутствие токов принцип суперпозиции гласит, что результирующее поле является суммой полей, генерируемых каждой частицей, как описано законом Кулона:

${displaystyle {oldsymbol {E}} ({oldsymbol {x}}) = {oldsymbol {E}} _ {1} ({oldsymbol {x}}) + {oldsymbol {E}} _ {2} ({oldsymbol { x}}) + {oldsymbol {E}} _ {3} ({oldsymbol {x}}) + cdots = {1 over 4pi varepsilon _ {0}} {q_ {1} over ({oldsymbol {x}} _ {1} - {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}} _ {1} + {1 over 4pi varepsilon _ {0}} {q_ {2} over ({oldsymbol { x}} _ {2} - {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}} _ {2} + {1 over 4pi varepsilon _ {0}} {q_ {3} over ({oldsymbol {x}} _ {3} - {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}} _ {3} + cdots}$

${displaystyle {oldsymbol {E}} ({oldsymbol {x}}) = {1 over 4pi varepsilon _ {0}} sum _ {k = 1} ^ {N} {q_ {k} over ({oldsymbol {x} } _ {k} - {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}} _ {k}}$

куда ${displaystyle {oldsymbol {{hat {r}} _ {k}}}}$ это единичный вектор в направлении от точки ${displaystyle {oldsymbol {x}} _ {k}}$ В точку ${displaystyle {oldsymbol {x}}}$.

Непрерывное распределение заряда

Принцип суперпозиции позволяет рассчитать электрическое поле из-за непрерывного распределения заряда. ${displaystyle ho ({oldsymbol {x}})}$ (куда ${displaystyle ho}$ это плотность заряда в кулонах на кубический метр). Учитывая обвинение ${displaystyle ho ({oldsymbol {x}} ') dV}$ в каждом небольшом объеме пространства ${displaystyle dV}$ в точке ${displaystyle {oldsymbol {x}} '}$ в качестве точечного заряда возникающее электрическое поле, ${displaystyle d {oldsymbol {E}} ({oldsymbol {x}})}$, в точке ${displaystyle {oldsymbol {x}}}$ можно рассчитать как

${displaystyle d {oldsymbol {E}} ({oldsymbol {x}}) = {1 over 4pi varepsilon _ {0}} {ho ({oldsymbol {x}} ') dV over ({oldsymbol {x}}' - {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}} '}$

куда ${displaystyle {hat {oldsymbol {r}}} '}$ это единичный вектор, указывающий из ${displaystyle {oldsymbol {x}} '}$ к ${displaystyle {oldsymbol {x}}}$. Общее поле затем находится путем "сложения" вкладов всех приращений объема на интеграция по объему распределения заряда ${displaystyle V}$:

${displaystyle {oldsymbol {E}} ({oldsymbol {x}}) = {1 over 4pi varepsilon _ {0}} iiint limits _ {V}, {ho ({oldsymbol {x}} ') dV over ({oldsymbol {x}} '- {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}}'}$

Аналогичные уравнения следуют для поверхностного заряда с непрерывным распределением заряда ${displaystyle sigma ({oldsymbol {x}})}$ куда ${displaystyle sigma}$ это плотность заряда в кулонах на квадратный метр

${displaystyle {oldsymbol {E}} ({oldsymbol {x}}) = {1 over 4pi varepsilon _ {0}} без ограничений _ {S}, {sigma ({oldsymbol {x}} ') dA over ({oldsymbol {x}} '- {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}}'}$

и для линейных зарядов с непрерывным распределением заряда ${displaystyle lambda ({oldsymbol {x}})}$ куда ${displaystyle lambda}$ - плотность заряда в кулонах на метр.

${displaystyle {oldsymbol {E}} ({oldsymbol {x}}) = {1 over 4pi varepsilon _ {0}} int limits _ {P}, {lambda ({oldsymbol {x}} ') dL over ({oldsymbol {x}} '- {oldsymbol {x}}) ^ {2}} {hat {oldsymbol {r}}}'}$

Электрический потенциал

Если система статична, так что магнитные поля не меняются во времени, то по закону Фарадея электрическое поле равно без завитков. В этом случае можно определить электрический потенциал, то есть функция ${displaystyle Phi}$ такой, что ${displaystyle mathbf {E} = -abla Phi}$.^[17] Это аналогично гравитационный потенциал. Разница между электрическим потенциалом в двух точках пространства называется разность потенциалов (или напряжение) между двумя точками.

Однако в целом электрическое поле нельзя описать независимо от магнитного поля. Учитывая магнитный векторный потенциал, А, определяется так, что ${displaystyle mathbf {B} = abla imes mathbf {A}}$, можно еще определить электрический потенциал ${displaystyle Phi}$ такой, что:

${displaystyle mathbf {E} = -abla Phi - {frac {partial mathbf {A}} {partial t}}}$

Где ${displaystyle abla Phi}$ это градиент электрического потенциала и ${displaystyle {frac {partial mathbf {A}} {partial t}}}$ это частная производная A по времени.

Закон индукции Фарадея можно восстановить, взяв завиток этого уравнения ^[18]

${displaystyle abla imes mathbf {E} = - {frac {partial (abla imes mathbf {A})} {partial t}} = - {frac {partial mathbf {B}} {partial t}}}$

что апостериори оправдывает предыдущую форму для E.

Непрерывное и дискретное представление заряда

Уравнения электромагнетизма лучше всего описывать в непрерывном описании. Однако иногда сборы лучше всего описывать как отдельные точки; например, некоторые модели могут описывать электроны как точечные источники, где плотность заряда бесконечна на бесконечно малом участке пространства.

Заряд ${displaystyle q}$ расположен в ${displaystyle mathbf {r_ {0}}}$ математически можно описать как плотность заряда ${displaystyle ho (mathbf {r}) = qdelta (mathbf {r-r_ {0}})}$, где Дельта-функция Дирака (в трех измерениях). И наоборот, распределение заряда можно аппроксимировать множеством мелких точечных зарядов.

Электростатические поля

Иллюстрация электрического поля, окружающего положительный (красный) и отрицательный (синий) заряд

Электростатические поля - это электрические поля, которые не меняются со временем, что происходит, когда заряды и токи неподвижны. В таком случае, Закон Кулона полностью описывает поле.^[19]

Параллели между электростатическим и гравитационным полями

Закон Кулона, описывающий взаимодействие электрических зарядов:

${displaystyle mathbf {F} = qleft ({frac {Q} {4pi varepsilon _ {0}}} {frac {mathbf {hat {r}}} {| mathbf {r} | ^ {2}}} ight) = qmathbf {E}}$

похоже на Закон всемирного тяготения Ньютона:

${displaystyle mathbf {F} = mleft (-GM {frac {mathbf {hat {r}}} {| mathbf {r} | ^ {2}}} ight) = mmathbf {g}}$

(куда ${displaystyle mathbf {hat {r}} = mathbf {frac {r} {| r |}}}$).

Это предполагает сходство между электрическим полем E и гравитационное поле грамм, или связанные с ними потенциалы. Масса иногда называется «гравитационным зарядом».^[20]

Электростатические и гравитационные силы действуют как центральный, консервативный и подчиняться закон обратных квадратов.

Единые поля

Иллюстрация электрического поля между двумя параллельными проводящий пластины конечного размера (известные как конденсатор с параллельными пластинами ). В середине пластин, вдали от краев, электрическое поле почти однородно.

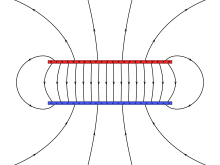
Однородное поле - это поле, в котором электрическое поле постоянно в каждой точке. Его можно приблизить, поместив два проводящих тарелки параллельно друг другу и поддерживая Напряжение (разность потенциалов) между ними; это только приближение из-за граничных эффектов (вблизи края плоскостей электрическое поле искажается, потому что плоскость не продолжается). В предположении бесконечности плоскостей величина электрического поля E является:

${displaystyle E = - {frac {Delta V} {d}}}$

где ΔV это разность потенциалов между пластинами и d расстояние между пластинами. Отрицательный знак возникает, когда положительные заряды отталкиваются, поэтому положительный заряд будет испытывать силу, направленную от положительно заряженной пластины, в направлении, противоположном тому, в котором увеличивается напряжение. В микро- и нано-приложениях, например, в отношении полупроводников, типичная величина электрического поля составляет порядка 10⁶ V⋅m⁻¹, достигаемого приложением напряжения порядка 1 вольт между проводниками, разнесенными на 1 мкм.

Электродинамические поля

Электрическое поле (линии со стрелками) заряда (+) вызывает поверхностные заряды (красный и синий области) на металлических предметах из-за электростатическая индукция.

Электродинамические поля - это электрические поля, которые меняются со временем, например, когда заряды находятся в движении. В этом случае создается магнитное поле в соответствии с Обходной закон Ампера (с добавлением Максвелла ), который, наряду с другими уравнениями Максвелла, определяет магнитное поле, ${displaystyle mathbf {B}}$, по завитку:

${displaystyle abla imes mathbf {B} = mu _ {0} left (mathbf {J} + varepsilon _ {0} {frac {partial mathbf {E}} {partial t}} ight)}$

, куда ${displaystyle mathbf {J}}$ это плотность тока, ${displaystyle mu _ {0}}$ это вакуумная проницаемость, и ${displaystyle varepsilon _ {0}}$ это диэлектрическая проницаемость вакуума.

То есть оба электрические токи (т.е. заряды в равномерном движении), и (частная) производная электрического поля по времени вносит непосредственный вклад в магнитное поле. В дополнение Уравнение Максвелла – Фарадея состояния

${displaystyle abla imes mathbf {E} = - {frac {partial mathbf {B}} {partial t}}}$

Это два из Четыре уравнения Максвелла и они замысловато связывают электрическое и магнитное поля вместе, в результате чего электромагнитное поле. Уравнения представляют собой набор из четырех связанных многомерных дифференциальных уравнений в частных производных, которые при решении для системы описывают комбинированное поведение электромагнитных полей. В общем, сила, испытываемая испытательным зарядом в электромагнитном поле, определяется как Закон силы Лоренца:

${displaystyle mathbf {F} = qmathbf {E} + qmathbf {v} imes mathbf {B}}$

Энергия в электрическом поле

Полная энергия на единицу объема, запасенная электромагнитное поле является^[21]

${displaystyle u_ {EM} = {frac {varepsilon} {2}} | mathbf {E} | ^ {2} + {frac {1} {2mu}} | mathbf {B} | ^ {2}}$

куда ε это диэлектрическая проницаемость среды, в которой существует поле, ${displaystyle mu}$ это магнитная проницаемость, и E и B - векторы электрического и магнитного полей.

В качестве E и B поля связаны, было бы ошибочным делить это выражение на «электрический» и «магнитный» вклады. Однако в стационарном случае поля больше не связаны (см. Уравнения Максвелла ). В этом случае имеет смысл вычислить электростатическую энергию на единицу объема:

${displaystyle u_ {ES} = {frac {1} {2}} varepsilon | mathbf {E} | ^ {2} ,,}$

Полная энергия U хранится в электрическом поле в заданном объеме V следовательно является

${displaystyle U_ {ES} = {frac {1} {2}} varepsilon int _ {V} | mathbf {E} | ^ {2}, mathrm {d} V ,,}$

Поле электрического смещения

Окончательное уравнение векторных полей

В присутствии вещества полезно расширить понятие электрического поля до трех векторных полей:^[22]

${displaystyle mathbf {D} = varepsilon _ {0} mathbf {E} + mathbf {P}!}$

куда п это электрическая поляризация - объемная плотность электрические дипольные моменты, и D это электрическое поле смещения. С E и п определяются отдельно, это уравнение можно использовать для определения D. Физическая интерпретация D не так ясно, как E (фактически поле, приложенное к материалу) или п (индуцированное поле из-за диполей в материале), но по-прежнему служит удобным математическим упрощением, поскольку уравнения Максвелла можно упростить в терминах бесплатные заряды и токи.

Учредительное отношение

В E и D поля связаны диэлектрическая проницаемость материала, ε.^[23][22]

Для линейного, однородный, изотропный материалы E и D пропорциональны и постоянны по всему региону, отсутствует позиционная зависимость:

${displaystyle mathbf {D (r)} = varepsilon mathbf {E (r)}}$

Для неоднородных материалов существует позиционная зависимость по всему материалу:^[24]

${displaystyle mathbf {D (r)} = varepsilon (mathbf {r}) mathbf {E (r)}}$

Для анизотропных материалов E и D поля не параллельны, поэтому E и D связаны тензор диэлектрической проницаемости (2-й порядок тензорное поле ), в компонентном виде:

${displaystyle D_ {i} = varepsilon _ {ij} E_ {j}}$

Для нелинейных сред E и D не пропорциональны. Материалы могут иметь различную степень линейности, однородности и изотропности.

Смотрите также

• Классический электромагнетизм
• электричество
• История электромагнитной теории
• Оптическое поле
• Магнетизм
• Трубка телтрона
• Teledeltos, токопроводящая бумага, которую можно использовать как простой аналоговый компьютер для моделирования полей.

Рекомендации

• Перселл, Эдвард; Морин, Дэвид (2013). ЭЛЕКТРИЧЕСТВО И МАГНИТИЗМ (3-е изд.). Издательство Кембриджского университета, Нью-Йорк. ISBN  978-1-107-01402-2.
• Браун, Майкл (2011). ФИЗИКА ДЛЯ ТЕХНИКИ И НАУКИ (2-е изд.). Макгроу-Хилл, Шаум, Нью-Йорк. ISBN  978-0-07-161399-6.

внешняя ссылка

• Электрическое поле в "Электричестве и магнетизме", R Nave – Гиперфизика, Государственный университет Джорджии
• Лекции Фрэнка Вольфса в Университет Рочестера, главы 23 и 24
• Поля - глава из онлайн-учебника