Емкость - Capacitance
Общие символы | C |
|---|---|
| Единица СИ | фарад |
Прочие единицы | мкФ, нФ, пФ |
| В Базовые единицы СИ | F = A2 s4 кг−1 м−2 |
Производные от другие количества | C = обвинять / Напряжение |
| Измерение | M−1 L−2 Т4 я2 |
Емкость это способность тела удерживать электрический заряд. В числовом выражении: это соотношение количества электрический заряд хранится на проводнике с разницей в электрический потенциал. Есть два тесно связанных понятия емкости: собственная емкость и взаимная емкость.[1]:237–238 Любой объект, который может быть электрически заряжен, выставляет собственная емкость. В этом случае измеряется разность электрических потенциалов между объектом и землей. Материал с большой собственной емкостью удерживает больше электрического заряда при заданном разность потенциалов чем один с низкой емкостью. Понятие взаимная емкость особенно важно для понимания работы конденсатор, один из трех элементарных линейный электронные компоненты (вместе с резисторы и индукторы ). В типичном конденсаторе два проводника используются для разделения электрического заряда, причем один проводник заряжен положительно, а другой - отрицательно, но система имеет нулевой общий заряд. Отношение в этом случае - это величина электрического заряда на любом проводнике, а разность потенциалов - это величина, измеренная между двумя проводниками.
Емкость зависит только от геометрии конструкции (например, площади пластин и расстояния между ними) и диэлектрическая проницаемость из диэлектрик материал между пластинами конденсатора. Для многих диэлектрических материалов диэлектрическая проницаемость и, следовательно, емкость не зависят от разности потенциалов между проводниками и общего заряда на них.
В SI единицей емкости является фарад (символ: F), названный в честь английского физика Майкл Фарадей. Конденсатор емкостью 1 фарад при зарядке 1 кулон электрического заряда, имеет разность потенциалов 1 вольт между его пластинами.[2] Обратная величина емкости называется эластичность.
Собственная емкость
В электрических схемах термин емкость обычно является сокращением для взаимная емкость между двумя соседними проводниками, такими как две пластины конденсатора. Однако для изолированного проводника также существует свойство, называемое собственная емкость, который представляет собой количество электрического заряда, которое необходимо добавить к изолированному проводнику, чтобы увеличить его электрический потенциал на одну единицу (то есть на один вольт в большинстве систем измерения).[3] Точкой отсчета для этого потенциала является теоретическая полая проводящая сфера бесконечного радиуса с проводником, центрированным внутри этой сферы.
Математически собственная емкость проводника определяется
куда
- q это заряд, удерживаемый на проводнике,
- электрический потенциал,
- σ - поверхностная плотность заряда.
- dS бесконечно малый элемент площади на поверхности проводника,
- р длина от dS до фиксированной точки M на дирижере
- это диэлектрическая проницаемость вакуума
Используя этот метод, собственная емкость проводящей сферы радиуса р является:[4]
Примеры значений собственной емкости:
- для верхней «тарелки» генератор Ван де Граафа, обычно сфера радиусом 20 см: 22,24 пФ,
- планета земной шар: около 710 мкФ.[5]
Межобмоточная емкость катушка иногда называют собственной емкостью,[6] но это другое явление. Это на самом деле взаимная емкость между отдельными витками катушки и является формой паразита, или паразитная емкость. Эта собственная емкость является важным фактором на высоких частотах: она изменяет сопротивление катушки и приводит к параллельному резонанс. Во многих приложениях это нежелательный эффект, который устанавливает верхний предел частоты для правильной работы схемы.[нужна цитата ]
Взаимная емкость
Распространенная форма - параллельная пластина. конденсатор, который состоит из двух проводящих пластин, изолированных друг от друга, обычно диэлектрик материал. В конденсаторе с параллельными пластинами емкость почти пропорциональна площади поверхности проводящих пластин и обратно пропорциональна расстоянию между пластинами.
Если заряды на пластинах +q и -q, и V дает Напряжение между пластинами, то емкость C дан кем-то
что дает напряжение /Текущий отношение
куда dv(т)/dт - мгновенная скорость изменения напряжения.
Энергия, запасенная в конденсаторе, определяется как интеграция работа W:
Матрица емкости
Вышеупомянутое обсуждение ограничено случаем двух проводящих пластин, хотя и произвольных размеров и форм. не применяется, когда имеется более двух заряженных пластин или когда чистый заряд на двух пластинах не равен нулю. Для рассмотрения этого дела Максвелл представил свой коэффициенты потенциала. Если зарядить три (почти идеальных) проводника , то напряжение на проводе 1 равно
и аналогично для других напряжений. Герман фон Гельмгольц и Сэр Уильям Томсон показал, что коэффициенты потенциала симметричны, так что и т. д. Таким образом, система может быть описана набором коэффициентов, известных как матрица упругости или же матрица обратной емкости, который определяется как:
Отсюда взаимная емкость между двумя объектами можно определить[7] решив на полную стоимость Q и используя .
Поскольку ни одно настоящее устройство не удерживает идеально равные и противоположные заряды на каждой из двух «пластин», на конденсаторах указывается взаимная емкость.
Сборник коэффициентов известен как матрица емкостей,[8][9] и это обратный матрицы упругости.
Конденсаторы
Емкость большинства конденсаторов, используемых в электронных схемах, обычно на несколько порядков меньше, чем у фарад. Наиболее часто используемые сегодня единицы емкости - это микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ), а в микросхемах фемтофарад (fF). Однако специально изготовленные суперконденсаторы могут быть намного больше (до сотен фарад), а паразитные емкостные элементы могут быть меньше фемтофарада. В прошлом альтернативные подразделения использовались в исторических электронных книгах; «mfd» и «mf» для микрофарад (мкФ); «mmfd», «mmf», «мкФ» для пикофарада (пФ); но уже редко используются.[10][11]
Емкость можно рассчитать, если известны геометрия проводников и диэлектрические свойства изолятора между проводниками. Качественное объяснение этому можно дать следующим образом.
Как только положительный заряд помещен в проводник, этот заряд создает электрическое поле, отталкивая любой другой положительный заряд, перемещающийся по проводнику; т.е. повышение необходимого напряжения. Но если рядом находится другой проводник с отрицательным зарядом на нем, электрическое поле положительного проводника, отталкивающее второй положительный заряд, ослабевает (второй положительный заряд также ощущает притягивающую силу отрицательного заряда). Таким образом, из-за того, что второй проводник имеет отрицательный заряд, становится легче поместить положительный заряд на уже положительно заряженный первый проводник, и наоборот; т.е. понижается необходимое напряжение.
В качестве количественного примера рассмотрим емкость конденсатора, состоящего из двух параллельных пластин, каждая из которых имеет площадь А разделенные расстоянием d. Если d достаточно мала относительно наименьшей хорды А, с высокой степенью точности:
куда
- C - емкость в фарадах;
- А - площадь перекрытия двух пластин в квадратных метрах;
- ε0 это электрическая постоянная (ε0 ≈ 8.854×10−12 F⋅m−1); и
- d расстояние между пластинами, в метрах;
Емкость пропорциональна площади перекрытия и обратно пропорциональна расстоянию между проводящими листами. Чем ближе листы друг к другу, тем больше емкость. Уравнение является хорошим приближением, если d мала по сравнению с другими размерами пластин, поэтому электрическое поле в области конденсатора является однородным, и так называемый окаймляющее поле по периферии дает лишь небольшой вклад в емкость.
Комбинируя уравнение для емкости с приведенным выше уравнением для энергии, запасенной в емкости, для конденсатора с плоской пластиной запасенная энергия составляет:
куда W энергия в джоулях; C - емкость в фарадах; и V напряжение в вольтах.
Паразитная емкость
Любые два соседних проводника могут функционировать как конденсатор, хотя емкость небольшая, если проводники не расположены близко друг к другу на больших расстояниях или на большой площади. Эта (часто нежелательная) емкость называется паразитной или паразитной емкостью. Паразитная емкость может привести к утечке сигналов между изолированными цепями (эффект, называемый перекрестные помехи ), и это может быть ограничивающим фактором для правильного функционирования цепей при высокая частота.
Паразитная емкость между входом и выходом в схемах усилителя может быть проблемой, поскольку может образовывать путь для Обратная связь, что может вызвать нестабильность и паразитные колебания в усилителе. Для аналитических целей часто бывает удобно заменить эту емкость комбинацией одной емкости входа-земли и одной емкости выхода-земли; исходная конфигурация, включая емкость входа-выхода, часто называется пи-конфигурацией. Теорема Миллера может быть использована для осуществления этой замены: она утверждает, что если коэффициент усиления двух узлов равен 1 /K, затем сопротивление из Z соединение двух узлов можно заменить на Z/(1 − k) импеданс между первым узлом и землей и KZ/(K - 1) полное сопротивление между вторым узлом и землей. Поскольку сопротивление изменяется обратно пропорционально емкости, межузловая емкость, C, заменяется емкостью KC от входа до земли и емкостью (K − 1)C/K от выхода к земле. Когда усиление вход-выход очень велико, эквивалентное сопротивление входа-земли очень мало, в то время как полное сопротивление выхода-земли по существу равно исходному (вход-выход) импедансу.
Емкость жил простой формы
Расчет емкости системы сводится к решению Уравнение лапласа ∇2φ = 0 с постоянным потенциалом φ на 2-мерной поверхности проводников, вложенных в 3-пространство. Это упрощается симметриями. В более сложных случаях нет решения в терминах элементарных функций.
Для плоских ситуаций могут использоваться аналитические функции для сопоставления различных геометрий друг другу. Смотрите также Отображение Шварца – Кристоффеля.
| Тип | Емкость | Комментарий |
|---|---|---|
| Параллельно-пластинчатый конденсатор | ||
| Концентрические цилиндры | 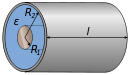 | |
| Пара параллельных проводов[12] |  | |
| Провод параллельно стене[12] | а: Радиус проволоки d: Расстояние, г> а ℓ: Длина провода | |
| Две параллельные копланарные полосы[13] | d: Расстояние ш1, w2: Ширина полосы kм: d / (2wм+ г) k2: k1k2 | |
| Концентрические сферы |  | |
| Две сферы, равный радиус[14][15] | а: Радиус d: Расстояние, d > 2а D = d/2а, D > 1 γ: Постоянная Эйлера | |
| Сфера перед стеной[14] | : Радиус : Расстояние, | |
| Сфера | : Радиус | |
| Круглый диск[16] | : Радиус | |
| Тонкая прямая проволока, конечная длина[17][18][19] | : Радиус проволоки : Длина |
Хранилище энергии
В энергия (измеряется в джоули ) хранится в конденсаторе, равно работай требуется для проталкивания зарядов в конденсатор, то есть для его зарядки. Рассмотрим конденсатор емкости C, держит заряд +q на одной тарелке и -q с другой. Перемещение небольшого элемента заряда dq от одной пластины к другой против разности потенциалов V = q / C требуется работа dW:
куда W работа измеряется в джоулях, q это заряд, измеренный в кулонах и C - емкость, измеряемая в фарадах.
Энергия, запасенная в конденсаторе, определяется как интеграция это уравнение. Начиная с незаряженной емкости (q = 0) и перемещая заряд с одной пластины на другую, пока пластины не будут заряжены +Q и -Q требует работы W:
Наноразмерные системы
Емкость наноразмерных диэлектрических конденсаторов, таких как квантовые точки могут отличаться от обычных составов конденсаторов большей емкости. В частности, электростатическая разность потенциалов, испытываемая электронами в обычных конденсаторах, пространственно четко определена и фиксируется формой и размером металлических электродов в дополнение к статистически большому количеству электронов, присутствующих в обычных конденсаторах. Однако в наноразмерных конденсаторах электростатические потенциалы, испытываемые электронами, определяются количеством и расположением всех электронов, которые вносят вклад в электронные свойства устройства. В таких устройствах количество электронов может быть очень небольшим, поэтому результирующее пространственное распределение эквипотенциальных поверхностей внутри устройства является чрезвычайно сложным.
Одноэлектронные устройства
Емкость подключенного или «замкнутого» одноэлектронного устройства в два раза больше емкости неподключенного или «открытого» одноэлектронного устройства.[20] Этот факт можно более фундаментально проследить за счет энергии, запасенной в одноэлектронном устройстве, энергия взаимодействия «прямой поляризации» которого может быть в равной степени разделена на взаимодействие электрона с поляризованным зарядом на самом устройстве из-за присутствия электрона и количество потенциальной энергии, необходимой для образования поляризованного заряда на устройстве (взаимодействие зарядов в диэлектрическом материале устройства с потенциалом, обусловленным электроном).[21]
Малоэлектронные устройства
Вывод «квантовой емкости» устройства с несколькими электронами включает термодинамический химический потенциал N-система частиц, задаваемая
чьи энергетические члены могут быть получены как решения уравнения Шредингера. Определение емкости,
- ,
с разностью потенциалов
может наноситься на устройство с добавлением или удалением отдельных электронов,
- и .
потом
это «квантовая емкость» устройства.[22]
Это выражение «квантовой емкости» можно записать как
которое отличается от обычного выражения, описанного во введении, где , запасенная электростатическая потенциальная энергия,
в 1/2 раза с .
Однако в рамках чисто классических электростатических взаимодействий появление множителя 1/2 является результатом интегрирования в традиционной формулировке:
что уместно, поскольку для систем, включающих либо много электронов, либо металлические электроды, но в системах с несколькими электронами, . Интеграл обычно становится суммой. Можно тривиально объединить выражения емкости и энергии электростатического взаимодействия:
- и ,
соответственно, чтобы получить
что аналогично квантовой емкости. В литературе сообщается о более строгом выводе.[23] В частности, чтобы обойти математические задачи сложных пространственно-сложных эквипотенциальных поверхностей внутри устройства, средний электростатический потенциал, испытываемый каждый электрон используется в выводе.
Явные математические различия понимаются более фундаментально как потенциальная энергия, , изолированного устройства (собственная емкость) вдвое больше, чем хранится в «подключенном» устройстве в нижнем пределе N= 1. В качестве N становится большим, .[21] Таким образом, общее выражение емкости есть
- .
В наноразмерных устройствах, таких как квантовые точки, «конденсатор» часто представляет собой изолированный или частично изолированный компонент внутри устройства. Основные различия между наноразмерными конденсаторами и макроскопическими (обычными) конденсаторами заключаются в количестве избыточных электронов (носителей заряда или электронов, которые влияют на электронное поведение устройства), а также в форме и размере металлических электродов. В наноразмерных устройствах нанопровода состоящие из атомов металлов, как правило, не обладают такими же проводящими свойствами, как их макроскопические или объемные материалы.
Емкость в электронных и полупроводниковых устройствах
В электронных и полупроводниковых устройствах переходный или частотно-зависимый ток между выводами содержит компоненты как проводимости, так и смещения. Ток проводимости связан с движущимися носителями заряда (электронами, дырками, ионами и т. Д.), А ток смещения вызван изменяющимся во времени электрическим полем. На перенос носителей влияют электрические поля и ряд физических явлений, таких как дрейф и диффузия носителей, захват, инжекция, эффекты, связанные с контактом, ударная ионизация и т. Д. В результате устройство допуск зависит от частоты, а простая электростатическая формула для емкости не применимо. Более общее определение емкости, охватывающее электростатическую формулу, таково:[24]
куда - пропускная способность устройства, а - угловая частота.
Как правило, емкость зависит от частоты. На высоких частотах емкость приближается к постоянному значению, равному «геометрической» емкости, которое определяется геометрией клемм и диэлектрическим содержанием в устройстве. Статья Стивена Лаукса[24] представляет собой обзор численных методов расчета емкости. В частности, емкость можно вычислить с помощью преобразования Фурье переходного тока в ответ на ступенчатое возбуждение напряжения:
Отрицательная емкость в полупроводниковых приборах
Обычно емкость в полупроводниковых приборах положительная. Однако в некоторых устройствах и при определенных условиях (температура, приложенное напряжение, частота и т. Д.) Емкость может стать отрицательной. Немонотонное поведение переходного тока в ответ на ступенчатое возбуждение было предложено в качестве механизма отрицательной емкости.[25] Отрицательная емкость была продемонстрирована и исследована во многих различных типах полупроводниковых устройств.[26]
Измерение емкости
А измеритель емкости это часть электронное испытательное оборудование используется для измерения емкости, в основном дискретных конденсаторы. В большинстве случаев и в большинстве случаев конденсатор должен быть отключен от схема.
Многие DVM (цифровые вольтметры ) имеют функцию измерения емкости. Обычно они работают, заряжая и разряжая конденсатор тестируемый с известным Текущий и измерение скорости роста результирующего Напряжение; чем медленнее скорость нарастания, тем больше емкость. DVM обычно могут измерять емкость от нанофарады до нескольких сотен микрофарад, но более широкие диапазоны не редкость. Также можно измерить емкость, пропустив известный высокая частота переменный ток через тестируемое устройство и измерение полученного Напряжение поперек него (не работает для поляризованных конденсаторов).

Более сложные приборы используют другие методы, такие как вставка тестируемого конденсатора в мостовая схема. Изменяя значения других ветвей моста (чтобы сбалансировать мост), определяется значение неизвестного конденсатора. Этот метод косвенный использование измерения емкости обеспечивает большую точность. За счет использования Кельвиновские связи и другие методы тщательного проектирования, эти инструменты обычно могут измерять конденсаторы в диапазоне от пикофарад до фарад.
Смотрите также
- Емкостной датчик перемещения
- Емкость комплекта
- Квантовая емкость
- Проводимость
- Ток смещения
- Обходной закон Ампера
- Закон Гаусса
- Гидравлическая аналогия
- Магнитная емкость
- Код РКМ
- Измеритель LCR
Рекомендации
- ^ Харрингтон, Роджер Ф. (2003). Введение в электромагнитную инженерию (1-е изд.). Dover Publications. п. 43. ISBN 0-486-43241-6.
- ^ "Определение слова" фарад "'". Коллинз.
- ^ Уильям Д. Гризон (1992). Электростатический разряд в электронике. Research Studies Press. п. 48. ISBN 978-0-86380-136-5.
- ^ Конспект лекций; Университет Нового Южного Уэльса
- ^ Типлер, Пол; Моска, Джин (2004). Физика для ученых и инженеров (5-е изд.). Макмиллан. п. 752. ISBN 978-0-7167-0810-0.
- ^ Massarini, A .; Казимерчук, М. (1997). «Собственная емкость индукторов». IEEE Transactions по силовой электронике. 12 (4): 671–676. Bibcode:1997ITPE ... 12..671M. CiteSeerX 10.1.1.205.7356. Дои:10.1109/63.602562: пример использования термина «собственная емкость».
- ^ Джексон, Джон Дэвид (1999). Классическая электродинамика (3-е изд.). Джон Вили и сыновья. п. 43. ISBN 978-0-471-30932-1.
- ^ Максвелл, Джеймс (1873). "3". Трактат об электричестве и магнетизме. 1. Кларендон Пресс. п. 88ff.
- ^ «Емкость: заряд как функция напряжения». Av8n.com. Получено 20 сентября 2010.
- ^ "Таблица преобразования конденсаторных MF-MMFD". Просто радио.
- ^ Основы электроники. Том 1b - Электричество - переменный ток. Бюро военно-морского персонала. 1965. с.197.
- ^ а б Джексон, Дж. Д. (1975). Классическая электродинамика. Вайли. п. 80.
- ^ Бинны; Лоуренсон (1973). Анализ и расчет задач электрического и магнитного поля. Pergamon Press. ISBN 978-0-08-016638-4.
- ^ а б Максвелл, Дж. К. (1873). Трактат об электричестве и магнетизме. Дувр. п. 266ff. ISBN 978-0-486-60637-8.
- ^ Роулинз, А. Д. (1985). «Заметка о емкости двух близко разделенных сфер». Журнал прикладной математики IMA. 34 (1): 119–120. Дои:10.1093 / imamat / 34.1.119.
- ^ Джексон, Дж. Д. (1975). Классическая электродинамика. Вайли. п. 128, проблема 3.3.
- ^ Максвелл, Дж. К. (1878). «Об электрической емкости длинного узкого цилиндра и диска ощутимой толщины». Proc. Лондонская математика. Soc. IX: 94–101. Дои:10.1112 / плмс / с1-9.1.94.
- ^ Вайнштейн, Л. А. (1962). «Статические краевые задачи для полого цилиндра конечной длины. III Приближенные формулы». Ж. Тех. Физ. 32: 1165–1173.
- ^ Джексон, Дж. Д. (2000). "Плотность заряда на тонком прямом проводе, еще раз". Являюсь. J. Phys. 68 (9): 789–799. Bibcode:2000AmJPh..68..789J. Дои:10.1119/1.1302908.
- ^ Рафаэль Цу (2011). От сверхрешетки к наноэлектронике. Эльзевир. С. 312–315. ISBN 978-0-08-096813-1.
- ^ а б Т. Лафэйв младший (2011). «Дискретно-зарядовая диэлектрическая модель электростатической энергии». J. Электростатика. 69 (6): 414–418. arXiv:1203.3798. Дои:10.1016 / j.elstat.2011.06.006. S2CID 94822190.
- ^ Г. Дж. Яфрате; К. Гесс; Дж. Б. Кригер; М. Макуччи (1995). «Емкостная природа структур атомных размеров». Phys. Ред. B. 52 (15): 10737–10739. Bibcode:1995PhRvB..5210737I. Дои:10.1103 / Physrevb.52.10737. PMID 9980157.
- ^ Т. Лафэйв младший; Р. Цу (март – апрель 2008 г.). «Емкость: свойство наноразмерных материалов, основанное на пространственной симметрии дискретных электронов» (PDF). Журнал микроэлектроники. 39 (3–4): 617–623. Дои:10.1016 / j.mejo.2007.07.105. Архивировано из оригинал (PDF) 22 февраля 2014 г.. Получено 12 февраля 2014.
- ^ а б Laux, S.E. (Октябрь 1985 г.). «Методы слабосигнального анализа полупроводниковых приборов». IEEE Transactions по автоматизированному проектированию интегральных схем и систем. 4 (4): 472–481. Дои:10.1109 / TCAD.1985.1270145. S2CID 13058472.
- ^ Йоншер, А. (1986). «Физическое происхождение отрицательной емкости». J. Chem. Soc. Faraday Trans. II. 82: 75–81. Дои:10.1039 / F29868200075.
- ^ Ершов, М .; Liu, H.C .; Li, L .; Бьюкенен, М .; Василевский, З.Р .; Йоншер, А. (Октябрь 1998 г.). «Эффект отрицательной емкости в полупроводниковых приборах». IEEE Trans. Электронные устройства. 45 (10): 2196–2206. arXiv:cond-mat / 9806145. Bibcode:1998ITED ... 45.2196E. Дои:10.1109/16.725254.
дальнейшее чтение
- Типлер, Пол (1998). Физика для ученых и инженеров: Вып. 2: Электричество и магнетизм, свет (4-е изд.). В. Х. Фриман. ISBN 1-57259-492-6
- Серуэй, Раймонд; Джуэтт, Джон (2003). Физика для ученых и инженеров (6-е изд.). Брукс Коул. ISBN 0-534-40842-7
- Саслоу, Уэйн М. (2002). Электричество, магнетизм и свет. Томсон обучения. ISBN 0-12-619455-6. См. Главу 8, и особенно стр. 255–259, где указаны коэффициенты потенциала.




































![{displaystyle {frac {2pi varepsilon ell }{Lambda }}left{1+{frac {1}{Lambda }}left(1-ln 2
ight)+{frac {1}{Lambda ^{2}}}left[1+left(1-ln 2
ight)^{2}-{frac {pi ^{2}}{12}}
ight]+Oleft({frac {1}{Lambda ^{3}}}
ight)
ight}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a19746fa861b22587cd9fbfcc0ed075187e6dc6a)



























![{displaystyle C(omega )=1/(Delta V)int _{0}^{infty }[i(t)-i(infty )]cos(omega t)dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ae46997077cb3776ef3946fcc54a8bd0e56d58c)