Эллиптический интеграл - Википедия - Elliptic integral

В интегральное исчисление, эллиптический интеграл является одной из ряда связанных функций, определяемых как значение определенных интегралов. Изначально они возникли в связи с проблемой поиска длина дуги из эллипс и впервые были изучены Джулио Фаньяно и Леонард Эйлер (c. 1750). Современная математика определяет «эллиптический интеграл» как любой функция ж который можно выразить в виде

${ Displaystyle е (х) = int _ {c} ^ {x} R left (t, { sqrt {P (t)}} right) , mathrm {d} t,}$

куда р это рациональная функция из двух его аргументов, п это многочлен степени 3 или 4 без повторяющихся корней, и c является константой.

В общем случае интегралы в таком виде не могут быть выражены через элементарные функции. Исключениями из этого общего правила являются случаи, когда п имеет повторяющиеся корни, или когда р(Икс,у) не содержит нечетных степеней у. Однако при соответствующем формула приведения, любой эллиптический интеграл можно привести к форме, включающей интегралы по рациональным функциям и трем Лежандровые канонические формы (т.е. эллиптические интегралы первого, второго и третьего рода).

Помимо формы Лежандра, приведенной ниже, эллиптические интегралы также могут быть выражены в Симметричная форма Карлсона. Дополнительное понимание теории эллиптического интеграла можно получить, изучив Отображение Шварца – Кристоффеля. Исторически, эллиптические функции были открыты как функции, обратные эллиптическим интегралам.

Обозначение аргумента

Неполные эллиптические интегралы являются функциями двух аргументов; полные эллиптические интегралы являются функциями одного аргумента. Эти аргументы выражаются различными, но эквивалентными способами (они дают один и тот же эллиптический интеграл). Большинство текстов придерживаются канонической схемы именования, используя следующие соглашения об именах.

Для выражения одного аргумента:

• α, то модульный угол
• k = грех α, то эллиптический модуль или же эксцентриситет
• м = k² = грех² α, параметр

Каждая из трех вышеупомянутых величин полностью определяется любой из других (при условии, что они неотрицательны). Таким образом, их можно использовать как взаимозаменяемые.

Другой аргумент можно также выразить как φ, то амплитуда, или как Икс или же ты, куда Икс = грех φ = sn ты и sn один из Эллиптические функции Якоби.

Указание значения одной из этих величин определяет остальные. Обратите внимание, что ты также зависит от м. Некоторые дополнительные отношения с участием ты включают

${ displaystyle cos varphi = operatorname {cn} u, quad { textrm {and}} quad { sqrt {1-m sin ^ {2} varphi}} = operatorname {dn} u .}$

Последний иногда называют дельта-амплитуда и написано как Δ (φ) = dn ты. Иногда в литературе также упоминается дополнительный параметр, то дополнительный модуль, или дополнительный модульный угол. Они более подробно описаны в статье о квартальные периоды.

Неполный эллиптический интеграл первого рода.

В неполный эллиптический интеграл первого рода F определяется как

${ Displaystyle F ( varphi, k) = F left ( varphi , | , k ^ {2} right) = F ( sin varphi; k) = int _ {0} ^ { varphi} { frac { mathrm {d} theta} { sqrt {1-k ^ {2} sin ^ {2} theta}}}.}.}$

Это тригонометрическая форма интеграла; замена т = грех θ и Икс = грех φ, получаем нормальную форму Лежандра:

${ Displaystyle F (х; к) = int _ {0} ^ {x} { frac { mathrm {d} t} { sqrt { left (1-t ^ {2} right) left (1-k ^ {2} t ^ {2} right)}}}.}$

Эквивалентно по амплитуде и модульному углу:

${ Displaystyle F ( varphi setminus alpha) = F ( varphi, sin alpha) = int _ {0} ^ { varphi} { frac { mathrm {d} theta} { sqrt {1 - ( sin theta sin alpha) ^ {2}}}}.}$

В этой нотации использование вертикальной черты в качестве разделителя указывает на то, что следующий за ней аргумент является «параметром» (как определено выше), а обратная косая черта указывает, что это модульный угол. Использование точки с запятой подразумевает, что предшествующий ей аргумент является синусом амплитуды:

${ Displaystyle F ( varphi, sin alpha) = F left ( varphi , | , sin ^ {2} alpha right) = F ( varphi setminus alpha) = F ( sin varphi; sin alpha).}$

Это потенциально сбивающее с толку использование различных разделителей аргументов является традиционным для эллиптических интегралов, и большая часть обозначений совместима с теми, которые используются в справочнике Абрамовиц и Стегун и тот, который используется в интегральных таблицах Градштейн и Рыжик.

С Икс = sn (ты,k) надо:

${ Displaystyle F (х; к) = и;}$

Таким образом Эллиптические функции Якоби обратны эллиптическим интегралам.

Варианты обозначений

В литературе существуют и другие соглашения об обозначении эллиптических интегралов. Обозначение с замененными аргументами, F(k,φ), часто встречается; и аналогично E(k,φ) для интеграла второго рода. Абрамовиц и Стегун подставляем интеграл первого рода, F(φ,k), для аргумента φ в их определении интегралов второго и третьего рода, если за этим аргументом не стоит вертикальная черта: т.е. E(F(φ,k) | k²) за E(φ | k²). Более того, их полные интегралы используют параметр k² в качестве аргумента вместо модуля k, т.е. K(k²) скорее, чем K(k). И интеграл третьего рода, определяемый формулой Градштейн и Рыжик, Π (φ,п,k), помещает амплитуду φ первая а не "характеристика" п.

Таким образом, при использовании этих функций следует соблюдать осторожность с обозначениями, поскольку в различных авторитетных источниках и программных пакетах используются разные соглашения в определениях эллиптических функций. Например, некоторые ссылки и Вольфрам с Mathematica программное обеспечение и вольфрам Альфа, определим полный эллиптический интеграл первого рода через параметр м, вместо эллиптического модуля k.

${ Displaystyle К (м) = int _ {0} ^ { tfrac { pi} {2}} { frac { mathrm {d} theta} { sqrt {1-m sin ^ {2 } theta}}}}$

Неполный эллиптический интеграл второго рода

В неполный эллиптический интеграл второго рода E в тригонометрической форме это

${ Displaystyle E ( varphi, k) = E left ( varphi , | , k ^ {2} right) = E ( sin varphi; k) = int _ {0} ^ { varphi} { sqrt {1-k ^ {2} sin ^ {2} theta}} , mathrm {d} theta.}$

Подстановка т = грех θ и Икс = грех φ, получаем нормальную форму Лежандра:

${ displaystyle E (x; k) = int _ {0} ^ {x} { frac { sqrt {1-k ^ {2} t ^ {2}}} { sqrt {1-t ^ { 2}}}} , mathrm {d} t.}$

Эквивалентно по амплитуде и модульному углу:

${ Displaystyle E ( varphi setminus alpha) = E ( varphi, sin alpha) = int _ {0} ^ { varphi} { sqrt {1- left ( sin theta sin alpha right) ^ {2}}} , mathrm {d} theta.}$

Отношения с Эллиптические функции Якоби включают

${ displaystyle E { bigl (} operatorname {sn} (u; k); k { bigr)} = int _ {0} ^ {u} operatorname {dn} ^ {2} (w; k ) , mathrm {d} w = uk ^ {2} int _ {0} ^ {u} operatorname {sn} ^ {2} (w; k) , mathrm {d} w = left (1-k ^ {2} right) u + k ^ {2} int _ {0} ^ {u} operatorname {cn} ^ {2} (w; k) , mathrm {d} w .}$

В дуга меридиана длина от экватор к широта φ написано в терминах E:

${ displaystyle m ( varphi) = a left (E ( varphi, e) + { frac { mathrm {d} ^ {2}} { mathrm {d} varphi ^ {2}}} E ( varphi, e) right),}$

куда а это большая полуось, и е это эксцентриситет.

Неполный эллиптический интеграл третьего рода

В неполный эллиптический интеграл третьего рода Π является

${ Displaystyle Pi (п; varphi setminus alpha) = int _ {0} ^ { varphi} { frac {1} {1-n sin ^ {2} theta}} { frac { mathrm {d} theta} { sqrt {1- left ( sin theta sin alpha right) ^ {2}}}}}$

или же

${ Displaystyle Pi (п; varphi , | , m) = int _ {0} ^ { sin varphi} { frac {1} {1-nt ^ {2}}} { frac { mathrm {d} t} { sqrt { left (1-mt ^ {2} right) left (1-t ^ {2} right)}}}.}$

Номер п называется характеристика и может принимать любое значение независимо от других аргументов. Обратите внимание, что значение Π (1; π/2 | м) бесконечно, для любого м.

Связь с эллиптическими функциями Якоби есть

${ Displaystyle Pi { bigl (} п; , operatorname {am} (u; k); , k { bigr)} = int _ {0} ^ {u} { frac { mathrm {d} w} {1-n , operatorname {sn} ^ {2} (w; k)}}.}$

Длина дуги меридиана от экватора до широты φ также относится к частному случаю Π:

${ displaystyle m ( varphi) = a left (1-e ^ {2} right) Pi left (e ^ {2}; varphi , | , e ^ {2} right). }$

Полный эллиптический интеграл первого рода

График полного эллиптического интеграла первого рода K(k)

Эллиптические интегралы называются полными, если амплитуда φ = π/2 и поэтому Икс = 1. В полный эллиптический интеграл первого рода K таким образом можно определить как

${ Displaystyle К (к) = int _ {0} ^ { tfrac { pi} {2}} { frac { mathrm {d} theta} { sqrt {1-k ^ {2} sin ^ {2} theta}}} = int _ {0} ^ {1} { frac { mathrm {d} t} { sqrt { left (1-t ^ {2} right) left (1-k ^ {2} t ^ {2} right)}}},}$

или, более компактно, в терминах неполного интеграла первого рода как

${ Displaystyle К (к) = F влево ({ tfrac { pi} {2}}, к вправо) = F влево ({ tfrac { pi} {2}} , | , к ^ {2} right) = F (1; k).}$

Это можно выразить как степенной ряд

${ displaystyle K (k) = { frac { pi} {2}} sum _ {n = 0} ^ { infty} left ({ frac {(2n)!} {2 ^ {2n} (n!) ^ {2}}} right) ^ {2} k ^ {2n} = { frac { pi} {2}} sum _ {n = 0} ^ { infty} { bigl (} P_ {2n} (0) { bigr)} ^ {2} k ^ {2n},}$

куда п_п это Полиномы Лежандра, что эквивалентно

${ displaystyle K (k) = { frac { pi} {2}} left (1+ left ({ frac {1} {2}} right) ^ {2} k ^ {2} + left ({ frac {1 cdot 3} {2 cdot 4}} right) ^ {2} k ^ {4} + cdots + left ({ frac { left (2n-1 right ) !!} { left (2n right) !!}} right) ^ {2} k ^ {2n} + cdots right),}$

куда п!! обозначает двойной факториал. В терминах Гаусса гипергеометрическая функция, полный эллиптический интеграл первого рода можно выразить как

${ Displaystyle К (к) = { tfrac { pi} {2}} , {} _ {2} F_ {1} left ({ tfrac {1} {2}}, { tfrac {1 } {2}}; 1; k ^ {2} right).}$

Полный эллиптический интеграл первого рода иногда называют четверть периода. Его можно очень эффективно вычислить с точки зрения среднее арифметико-геометрическое:

${ displaystyle K (k) = { frac { frac { pi} {2}} { operatorname {agm} left (1, { sqrt {1-k ^ {2}}} right)} }.}$

Видеть Карлсон (2010), 19.8) для подробностей.

Связь с тета-функцией Якоби

Отношение к Тета-функция Якоби дан кем-то

${ Displaystyle К (к) = { гидроразрыва { pi} {2}} theta _ {3} ^ {2} (q),}$

где ном q является

${ displaystyle q (k) = exp left (- pi { frac {K left ({ sqrt {1-k ^ {2}}} right)} {K (k)}} right ).}$

Асимптотические выражения

${ displaystyle K left (k right) приблизительно { frac { pi} {2}} + { frac { pi} {8}} { frac {k ^ {2}} {1-k ^ {2}}} - { frac { pi} {16}} { frac {k ^ {4}} {1-k ^ {2}}}}$

Это приближение имеет относительную точность лучше, чем 3×10⁻⁴ за k < 1/2. Сохранение только первых двух членов является правильным с точностью до 0,01 для k < 1/2.^{[нужна цитата ]}

Дифференциальное уравнение

Дифференциальное уравнение для эллиптического интеграла первого рода имеет вид

${ displaystyle { frac { mathrm {d}} { mathrm {d} k}} left (k left (1-k ^ {2} right) { frac { mathrm {d} K ( k)} { mathrm {d} k}} right) = kK (k)}$

Второе решение этого уравнения: ${ displaystyle K left ({ sqrt {1-k ^ {2}}} right)}$. Это решение удовлетворяет соотношению

${ Displaystyle { гидроразрыва { mathrm {d}} { mathrm {d} k}} K (k) = { frac {E (k)} {k left (1-k ^ {2} right )}} - { frac {K (k)} {k}}.}$

Полный эллиптический интеграл второго рода

График полного эллиптического интеграла второго рода ${ displaystyle E (k)}$

В полный эллиптический интеграл второго рода E определяется как

${ displaystyle E (k) = int _ {0} ^ { tfrac { pi} {2}} { sqrt {1-k ^ {2} sin ^ {2} theta}} , mathrm {d} theta = int _ {0} ^ {1} { frac { sqrt {1-k ^ {2} t ^ {2}}} { sqrt {1-t ^ {2}} }} , mathrm {d} t,}$

или более компактно в терминах неполного интеграла второго рода E(φ,k) в качестве

${ Displaystyle E (k) = E left ({ tfrac { pi} {2}}, k right) = E (1; k).}$

Для эллипса с большой полуосью а и малая полуось б и эксцентриситет е = √1 − б²/а², полный эллиптический интеграл второго рода E(е) равен одной четверти длина окружности c эллипса в единицах большой полуоси а. Другими словами:

${ displaystyle c = 4aE (e).}$

Полный эллиптический интеграл второго рода можно выразить как степенной ряд

${ displaystyle E (k) = { frac { pi} {2}} sum _ {n = 0} ^ { infty} left ({ frac {(2n)!} {2 ^ {2n} left (n! right) ^ {2}}} right) ^ {2} { frac {k ^ {2n}} {1-2n}},}$

что эквивалентно

${ displaystyle E (k) = { frac { pi} {2}} left (1- left ({ frac {1} {2}} right) ^ {2} { frac {k ^ {2}} {1}} - left ({ frac {1 cdot 3} {2 cdot 4}} right) ^ {2} { frac {k ^ {4}} {3}} - cdots - left ({ frac {(2n-1) !!} {(2n) !!}} right) ^ {2} { frac {k ^ {2n}} {2n-1}} - cdots right).}$

Что касается Гипергеометрическая функция Гаусса, полный эллиптический интеграл второго рода можно выразить как

${ displaystyle E (k) = { tfrac { pi} {2}} , {} _ {2} F_ {1} left ({ tfrac {1} {2}}, - { tfrac { 1} {2}}; 1; k ^ {2} right).}$

Вычисление

Как и интеграл первого рода, полный эллиптический интеграл второго рода может быть очень эффективно вычислен с использованием среднего арифметико-геометрического (Карлсон 2010, 19.8).

Определить последовательности ${ displaystyle a_ {n}}$ и ${ displaystyle g_ {n}}$, куда ${ displaystyle a_ {0} = 1}$, ${ displaystyle g_ {0} = { sqrt {1-k ^ {2}}} = k '}$ и рекуррентные отношения ${ displaystyle a_ {n + 1} = { frac {a_ {n} + g_ {n}} {2}}}$, ${ displaystyle g_ {n + 1} = { sqrt {a_ {n} g_ {n}}}}$ держать. Кроме того, определим ${ displaystyle c_ {n} = { sqrt { left | a_ {n} ^ {2} -g_ {n} ^ {2} right |}}}$. По определению,

${ displaystyle a _ { infty} = lim _ {n to infty} a_ {n} = lim _ {n to infty} g_ {n} = operatorname {agm} (1, { sqrt {1-k ^ {2}}})}$.

Также, ${ displaystyle lim _ {n to infty} c_ {n} = 0}$. потом

${ displaystyle E (k) = { frac { pi} {2a _ { infty}}} left (1- sum _ {n = 0} ^ { infty} 2 ^ {n-1} c_ { n} ^ {2} right).}$

На практике среднее арифметико-геометрическое будет просто вычисляться до некоторого предела. Эта формула сходится квадратично для всех ${ Displaystyle | к | leq 1}$. Для дальнейшего ускорения вычислений соотношение ${ displaystyle c_ {n + 1} = { frac {c_ {n} ^ {2}} {4a_ {n + 1}}}}$ может быть использован.

Производное и дифференциальное уравнение

${ Displaystyle { frac { mathrm {d} E (k)} { mathrm {d} k}} = { frac {E (k) -K (k)} {k}}}$

${ displaystyle left (k ^ {2} -1 right) { frac { mathrm {d}} { mathrm {d} k}} left (k ; { frac { mathrm {d}) E (k)} { mathrm {d} k}} right) = kE (k)}$

Второе решение этого уравнения: E(√1 − k²) − K(√1 − k²).

Полный эллиптический интеграл третьего рода

График полного эллиптического интеграла третьего рода ${ Displaystyle Pi (п, к)}$ с несколькими фиксированными значениями ${ displaystyle n}$

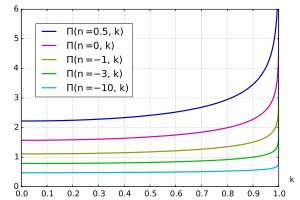
В полный эллиптический интеграл третьего рода Π можно определить как

${ displaystyle Pi (n, k) = int _ {0} ^ { tfrac { pi} {2}} { frac { mathrm {d} theta} { left (1-n sin ^ {2} theta right) { sqrt {1-k ^ {2} sin ^ {2} theta}}}}.}.}$

Отметим, что иногда эллиптический интеграл третьего рода определяется с обратным знаком для характеристика п,

${ displaystyle Pi '(n, k) = int _ {0} ^ { tfrac { pi} {2}} { frac { mathrm {d} theta} { left (1 + n sin ^ {2} theta right) { sqrt {1-k ^ {2} sin ^ {2} theta}}}}.}.$

Как и полные эллиптические интегралы первого и второго рода, полный эллиптический интеграл третьего рода может быть очень эффективно вычислен с использованием среднего арифметико-геометрического (Карлсон 2010, 19.8).

Частные производные

${ displaystyle { begin {align} { frac { partial Pi (n, k)} { partial n}} & = { frac {1} {2 left (k ^ {2} -n справа) (n-1)}} left (E (k) + { frac {1} {n}} left (k ^ {2} -n right) K (k) + { frac {1 } {n}} left (n ^ {2} -k ^ {2} right) Pi (n, k) right) [10px] { frac { partial Pi (n, k) } { partial k}} & = { frac {k} {nk ^ {2}}} left ({ frac {E (k)} {k ^ {2} -1}} + Pi (n , л) право) конец {выровнено}}}$

Функциональные отношения

Отношение Лежандра:

${ Displaystyle К (к) E влево ({ sqrt {1-k ^ {2}}} right) + E (k) K left ({ sqrt {1-k ^ {2}}} right) -K (k) K left ({ sqrt {1-k ^ {2}}} right) = { frac { pi} {2}}.}$

Смотрите также

Рекомендации

• Абрамовиц, Милтон; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. "Глава 17". Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972); первое изд.) Вашингтон, округ Колумбия.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 587. ISBN  978-0-486-61272-0. LCCN  64-60036. МИСТЕР  0167642. LCCN  65-12253.
• Берд, П. Ф .; Фридман, доктор медицины (1971). Справочник по эллиптическим интегралам для инженеров и ученых (2-е изд.). Нью-Йорк: Springer-Verlag. ISBN  0-387-05318-2.
• Карлсон, Б.С. (1995). «Численное вычисление действительных или комплексных эллиптических интегралов». Численные алгоритмы. 10 (1): 13–26. arXiv:математика / 9409227. Bibcode:1995 НуАлг..10 ... 13С. Дои:10.1007 / BF02198293.
• Карлсон, Б.С. (2010), «Эллиптический интеграл», в Олвер, Фрэнк В. Дж.; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Издательство Кембриджского университета, ISBN  978-0-521-19225-5, МИСТЕР  2723248
• Эрдейи, Артур; Магнус, Вильгельм; Оберхеттингер, Фриц; Трикоми, Франческо Г. (1953). Высшие трансцендентные функции. Том II (PDF). McGraw-Hill Book Company, Inc., Нью-Йорк-Торонто-Лондон. МИСТЕР  0058756.
• Градштейн Израиль Соломонович; Рыжик Иосиф Моисеевич; Геронимус Юрий Вениаминович; Цейтлин Михаил Юльевич; Джеффри, Алан (2015) [октябрь 2014]. «8.1.». В Цвиллингере, Даниэль; Молл, Виктор Гюго (ред.). Таблица интегралов, серий и продуктов. Перевод Scripta Technica, Inc. (8-е изд.). Academic Press, Inc. ISBN  978-0-12-384933-5. LCCN  2014010276.
• Гринхилл, Альфред Джордж (1892). Приложения эллиптических функций. Нью-Йорк: Макмиллан.
• Хэнкок, Харрис (1910). Лекции по теории эллиптических функций. Нью-Йорк: J. Wiley & sons.
• Король, Людовик V. (1924). О прямом численном вычислении эллиптических функций и интегралов. Издательство Кембриджского университета.
• Press, W. H .; Теукольский, С. А .; Vetterling, W. T .; Фланнери, Б. П. (2007), «Раздел 6.12. Эллиптические интегралы и эллиптические функции якоби», Числовые рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Издательство Кембриджского университета, ISBN  978-0-521-88068-8

внешняя ссылка

• «Эллиптический интеграл», Энциклопедия математики, EMS Press, 2001 [1994]
• Эрик В. Вайсштейн, "Эллиптический интеграл" (Mathworld)
• Код Matlab для вычисления эллиптических интегралов по эллиптическому проекту
• Рациональные приближения для полных эллиптических интегралов. (Лаборатории Exstrom)
• Краткая история эллиптических теорем интегрального сложения