Широта - Latitude

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: "Широта"  – Новости  · газеты  · книги  · ученый  · JSTOR (Февраль 2019 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

А сетка на Земле как сфера или эллипсоид. Линии от полюса к полюсу - это линии постоянного долгота, или же меридианы. Круги, параллельные экватор линии постоянной широты, или параллели. Сетка показывает широту и долготу точек на поверхности. В этом примере меридианы расположены с интервалом 6 °, а параллели - с интервалом 4 °.

В география, широта это географическая координата что определяет север –юг положение точки на поверхности Земли. Широта - это угол (определенный ниже), который колеблется от 0 ° на Экватор до 90 ° (север или юг) на полюсах. Линии постоянной широты, или параллели, бегите с востока на запад в виде кругов, параллельных экватору. Локатор используется вместе с долгота для указания точного местоположения объектов на поверхности Земли. Сам по себе термин широта следует понимать как геодезическая широта как определено ниже. Вкратце, геодезическая широта в точке - это угол, образованный перпендикуляром вектора (или нормальный ) к эллипсоидальной поверхности от этой точки и к экваториальной плоскости. Также определены шесть вспомогательные широты которые используются в специальных приложениях.

Предварительные мероприятия

При определении широты и долготы используются два уровня абстракции. На первом этапе физическая поверхность моделируется геоид, поверхность, аппроксимирующая средний уровень моря над океанами и его продолжение под сушей. Второй шаг состоит в аппроксимации геоида с помощью математически простой опорной поверхности. Самый простой выбор для опорной поверхности является сфера, но геоид более точно моделируется эллипсоидом. Определения широты и долготы на таких опорных поверхностях подробно описаны в следующих разделах. Линии постоянной широты и долготы вместе составляют сетка на эталонной поверхности. Широта точки на действительный Поверхность является то, что соответствующей точки на опорной поверхности, соответствие быть вдоль нормальный к базовой поверхности, которая проходит через точку на физической поверхности. Широта и долгота вместе с некоторыми указаниями высота составляют географическая система координат как определено в спецификации стандарта ISO 19111.^[а]

Поскольку есть много разных справочные эллипсоиды, точная широта объекта на поверхности не является уникальной: это подчеркивается в стандарте ISO, который гласит, что «без полной спецификации системы координат координаты (то есть широта и долгота) в лучшем случае неоднозначны и бессмысленны в наихудший". Это очень важно для точных приложений, таких как спутниковая система навигации (GPS), но при обычном использовании, где не требуется высокая точность, опорный эллипсоид обычно не указывается.

В английских текстах угол широты, определяемый ниже, обычно обозначается строчной греческой буквой. фи (φ или же ϕ). Он измеряется в градусы, минуты и секунды или же десятичные градусы, к северу или югу от экватора. Для целей навигации позиции указываются в градусах и десятичных минутах. Например, маяк Иглы находится на 50 ° 39,734'N 001 ° 35,500'W.^[1]

Точное измерение широты требует понимания гравитационного поля Земли, либо для настройки теодолиты или для определения спутниковых орбит GPS. Изучение фигура земли вместе с его гравитационным полем - это наука о геодезия.

Эта статья относится к системам координат для Земли: она может быть расширена для охвата Луны, планет и других небесных объектов путем простого изменения номенклатуры.

Широта на сфере

Перспективный вид Земли, показывающий, насколько широта (${displaystyle phi}$) и долгота (${displaystyle lambda}$) определены на сферической модели. Шаг сетки 10 градусов.

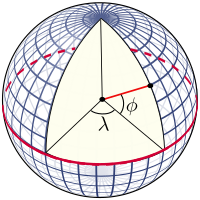
Сетка на сфере

Масштабная сетка образована линиями постоянной широты и постоянной долготы, которые построены относительно оси вращения Земли. Основными ориентирами являются полюса где ось вращения Земли пересекает опорную поверхность. Плоскости, содержащие ось вращения, пересекают поверхность в точках меридианы; и угол между любой плоскостью меридиана и плоскостью, проходящей через Гринвич ( нулевой меридиан ) определяет долготу: меридианы - это линии постоянной долготы. Плоскость, проходящая через центр Земли и перпендикулярная оси вращения, пересекает поверхность по большому кругу, называемому Экватор. Плоскости, параллельные экваториальной плоскости, пересекают поверхность кругами постоянной широты; это параллели. Экватор имеет широту 0 °, Северный полюс имеет широту 90 ° северной широты (записывается 90 ° N или + 90 °), а Южный полюс имеет широту 90 ° южной широты (записывается 90 ° южной широты или -90 °). Широта произвольной точки - это угол между плоскостью экватора и нормалью к поверхности в этой точке: нормаль к поверхности сферы проходит по радиус-вектору.

Широту, как определено таким образом для сферы, часто называют сферической широтой, чтобы избежать неоднозначности с геодезической широтой и вспомогательными широтами, определенными в последующих разделах этой статьи.

Названные широты на Земле

Ориентация Земли в день декабрьского солнцестояния.

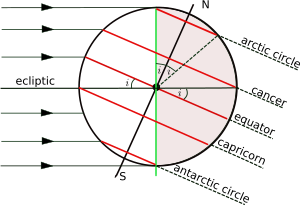
Помимо экватора, важны еще четыре параллели:

Полярный круг	66 ° 34 '(66,57 °) с.ш.
Тропик Рака	23 ° 26 '(23,43 °) с.ш.
Тропик Козерога	23 ° 26 '(23,43 °) ю.ш.
Южный полярный круг	66 ° 34 '(66,57 °) ю.ш.

Плоскость орбиты Земли вокруг Солнца называется эклиптика, а плоскость, перпендикулярная оси вращения Земли, - это экваториальная плоскость. Угол между эклиптикой и экваториальной плоскостью называется по-разному осевым наклоном, наклоном или наклоном эклиптики и обычно обозначается как я. Широта тропических кругов равна я а широта полярных кругов - его дополнение (90 ° - я). Ось вращения медленно меняется со временем, и значения, приведенные здесь, являются значениями для текущего эпоха. Изменение во времени более подробно обсуждается в статье о осевой наклон.^[b]

На рисунке показана геометрия поперечное сечение плоскости, перпендикулярной эклиптике и проходящей через центры Земли и Солнца в декабре солнцестояние когда Солнце находится над головой в какой-то точке Тропик Козерога. Южные полярные широты ниже Южный полярный круг днем, а в северных полярных широтах за Полярным кругом - ночью. Ситуация меняется на противоположную во время июньского солнцестояния, когда Солнце находится над головой в тропике Рака. Только на широте между двумя тропики возможно ли, чтобы Солнце находилось прямо над головой (на зенит ).

На картографические проекции не существует универсального правила того, как должны выглядеть меридианы и параллели. В приведенных ниже примерах показаны именованные параллели (в виде красных линий) на часто используемых Проекция Меркатора и Поперечная проекция Меркатора. На первом параллели горизонтальны, а меридианы вертикальны, тогда как на втором нет точного соотношения параллелей и меридианов с горизонталью и вертикалью: оба являются сложными кривыми.

	Нормальный Меркатор		Поперечный Меркатор

Расстояние по меридиану на сфере

На сфере нормаль проходит через центр и широту (φ), следовательно, равен углу, образуемому в центре дугой меридиана от экватора до рассматриваемой точки. Если меридианное расстояние обозначается м(φ) тогда

${displaystyle m (phi) = {frac {pi} {180 ^ {circ}}} Rphi _ {mathrm {градусов}} = Rphi _ {mathrm {радианы}}}$

куда р обозначает средний радиус земли. р равно 6 371 км или 3959 миль. Для р поскольку для получения более точных результатов требуется модель эллипсоида. С этим значением для р Длина меридиана 1 градуса широты на сфере составляет 111,2 км (69,1 статутной мили) (60,0 морских миль). Длина 1 минуты широты составляет 1,853 км (1,151 статутной мили) (1,00 морская миля), а длина 1 секунды широты составляет 30,8 м или 101 фут (см. морская миля ).

Широта на эллипсоиде

Эллипсоиды

В 1687 г. Исаак Ньютон опубликовал Philosophiæ Naturalis Principia Mathematica, в котором он доказал, что вращающееся самогравитирующее жидкое тело в состоянии равновесия принимает форму сплюснутый эллипсоид.^[2] (В этой статье используется термин эллипсоид в предпочтении к старому термину сфероид.) Результат Ньютона был подтвержден геодезическими измерениями в 18 веке. (Видеть Дуга меридиана.) Сплюснутый эллипсоид - это трехмерная поверхность, образованная вращением эллипса вокруг его более короткой оси (малой оси). «Сплюснутый эллипсоид вращения» в оставшейся части этой статьи сокращенно обозначается словом «эллипсоид». (Эллипсоиды, не имеющие оси симметрии, называются трехосными.)

Много разных справочные эллипсоиды были использованы в истории геодезия. В доспутниковые дни они были созданы, чтобы хорошо подходить к геоид на ограниченной области исследования, но с появлением GPS, стало естественным использовать справочные эллипсоиды (например, WGS84 ) с центром в центре масс Земли и малой осью, совмещенной с осью вращения Земли. Эти геоцентрические эллипсоиды обычно находятся в пределах 100 м (330 футов) от геоида. Поскольку широта определяется относительно эллипсоида, положение данной точки на каждом эллипсоиде отличается: нельзя точно указать широту и долготу географического объекта, не указав используемый эллипсоид. Многие карты, поддерживаемые национальными агентствами, основаны на старых эллипсоидах, поэтому необходимо знать, как значения широты и долготы преобразуются из одного эллипсоида в другой. Трубки GPS включают программное обеспечение для выполнения преобразования датума которые связывают WGS84 с эллипсоидом локальной ссылки с соответствующей сеткой.

Геометрия эллипсоида

Сфера радиуса а сжатый вдоль z ось, чтобы сформировать сплюснутый эллипсоид вращения.

Форма эллипсоида вращения определяется формой эллипс который вращается вокруг своей малой (более короткой) оси. Требуются два параметра. Один из них - это всегда экваториальный радиус, т.е. большая полуось, а. Другой параметр обычно (1) полярный радиус или малая полуось, б; или (2) (первый) сплющивание, ж; или (3) эксцентриситет, е. Эти параметры не являются независимыми: они связаны соотношением

${displaystyle f = {frac {ab} {a}}, qquad e ^ {2} = 2f-f ^ {2}, qquad b = a (1-f) = a {sqrt {1-e ^ {2} }} ,.}$

Многие другие параметры (см. эллипс, эллипсоид ) появляются при изучении геодезии, геофизики и картографических проекций, но все они могут быть выражены в терминах одного или двух членов множества а, б, ж и е. Обе ж и е малы и часто появляются в расчетах в виде разложения в ряды; они в порядке 1/298 и 0,0818 соответственно. Значения для ряда эллипсоидов приведены в Фигура Земли. Справочные эллипсоиды обычно определяются большой полуосью и обратный сплющивание, 1/ж. Например, определяющие значения для WGS84 эллипсоид, используемый всеми устройствами GPS,^[3]

• а (экваториальный радиус): 63781370,0 м точно
• 1/ж (обратное сплющивание): 298.257223563 точно

из которых происходят

• б (полярный радиус): 63567520,3142 м
• е² (квадрат эксцентриситета): 0.00669437999014

Разница между большой и малой полуосями составляет около 21 км (13 миль), и как часть большой полуоси она равна уплощению; на мониторе компьютера эллипсоид может иметь размер 300 на 299 пикселей. Его едва ли можно отличить от сферы размером 300 на 300 пикселей, поэтому иллюстрации обычно преувеличивают сглаживание.

Геодезические и геоцентрические широты

Определение геодезической широты (${displaystyle phi}$) и долгота (${displaystyle lambda}$) на эллипсоиде. Нормаль к поверхности не проходит через центр, за исключением экватора и полюсов.

Сетка на эллипсоиде строится точно так же, как на сфере. Нормаль в точке на поверхности эллипсоида не проходит через центр, за исключением точек на экваторе или полюсах, но определение широты остается неизменным как угол между нормалью и экваториальной плоскостью. Терминологию широты необходимо уточнить, выделив:

• Геодезическая широта: угол между нормалью и экваториальной плоскостью. Стандартное обозначение в английских публикациях: φ. Это определение предполагается, когда слово широта используется без уточнения. Определение должно сопровождаться спецификацией эллипсоида.
• Геоцентрическая широта: угол между радиусом (от центра до точки на поверхности) и экваториальной плоскостью. (Фигура ниже ). Стандартных обозначений нет: примеры из разных текстов включают θ, ψ, q, φ ′, φ_c, φ_грамм. В этой статье используется θ.
• Сферическая широта: угол между нормалью к сферической опорной поверхности и экваториальная плоскость.
• Географическая широта следует использовать с осторожностью. Некоторые авторы используют его как синоним геодезической широты, в то время как другие используют его как альтернативу геодезической широте. астрономическая широта.
• Широта (неквалифицированный) обычно относится к геодезической широте.

Важность указания опорных данных можно проиллюстрировать на простом примере. На референц-эллипсоида для WGS84, в центре Эйфелева башня имеет геодезическую широту 48 ° 51 ′ 29 ″ N или 48,8583 ° N и долготу 2 ° 17 ′ 40 ″ E или 2,2944 ° E. Те же координаты на датуме ED50 определите точку на земле, которая находится на расстоянии 140 метров (460 футов) от башни.^{[нужна цитата ]} Веб-поиск может дать несколько разных значений широты башни; эллипсоид ссылки указывается редко.

Длина градуса широты

В Дуга меридиана и стандартные тексты^[4][5][6] показано, что расстояние по меридиану от широты φ к экватору определяется выражением (φ в радианах)

${displaystyle m (phi) = int _ {0} ^ {phi} M (phi '), dphi' = aleft (1-e ^ {2} ight) int _ {0} ^ {phi} left (1-e ^ {2} sin ^ {2} phi 'ight) ^ {- {frac {3} {2}}}, dphi'}$

куда M(φ) меридиональный радиус кривизны.

Расстояние от экватора до полюса

${displaystyle m_ {mathrm {p}} = mleft ({frac {pi} {2}} ight),}$

За WGS84 это расстояние 10001.965729 км.

Оценка интеграла меридионального расстояния занимает центральное место во многих исследованиях в области геодезии и картографии. Его можно вычислить, разложив интеграл биномиальным рядом и интегрировав почленно: см. Дуга меридиана для подробностей. Длина дуги меридиана между двумя заданными широтами определяется заменой пределов интеграла соответствующими широтами. Длина маленький дуга меридиана определяется выражением^[5][6]

${displaystyle delta m (phi) = M (phi), delta phi = aleft (1-e ^ {2} ight) left (1-e ^ {2} sin ^ {2} phi ight) ^ {- {frac { 3} {2}}}, дельта-фи}$

${displaystyle phi}$	Δ1 широта	Δ1 длинный
0°	110.574 км	111.320 км
15°	110.649 км	107.550 км
30°	110.852 км	96.486 км
45°	111.132 км	78.847 км
60°	111.412 км	55.800 км
75°	111.618 км	28.902 км
90°	111.694 км	0.000 км

Когда разница широты составляет 1 градус, что соответствует π/180 радиан, расстояние по дуге составляет около

${displaystyle Delta _ {ext {lat}} ^ {1} = {frac {pi aleft (1-e ^ {2} ight)} {180 ^ {circ} left (1-e ^ {2} sin ^ {2 } phi ight) ^ {гидроразрыв {3} {2}}}}}$

Расстояние в метрах (с точностью до 0,01 метра) между широтами. ${displaystyle phi}$ - 0,5 градуса и ${displaystyle phi}$ + 0,5 градуса на сфероиде WGS84

${displaystyle Delta _ {ext {lat}} ^ {1} = 111,132.954-559.822cos 2phi + 1.175cos 4phi}$

Изменение этого расстояния с широтой (на WGS84 ) показан в таблице вместе с длина градуса долготы (расстояние с востока на запад):

${displaystyle Delta _ {ext {long}} ^ {1} = {frac {pi acos phi} {180 ^ {circ} {sqrt {1-e ^ {2} sin ^ {2} phi}}}},}$

Калькулятор для любой широты предоставлен правительством США. Национальное агентство геопространственной разведки (NGA).^[7]

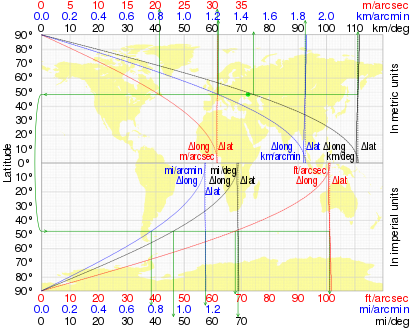
На следующем графике показано изменение градуса широты и долготы в зависимости от широты.

Определение геодезической широты (φ) и геоцентрической широты (θ).

Морская миля

Исторически морская миля была определена как длина одной угловой минуты вдоль меридиана сферической Земли. Модель эллипсоида приводит к изменению морской мили в зависимости от широты. Это было решено путем определения морской мили равной 1852 метрам. Однако для всех практических целей расстояния измеряются по шкале географических широт. Поскольку Королевская яхтенная ассоциация говорит в своем руководстве для дневные шкиперы: «1 (минута) широты = 1 морская миля», за которым следует «Для большинства практических целей расстояние измеряется по шкале широты, предполагая, что одна минута широты равна одной морской миле».^[8]

Вспомогательные широты

Шесть вспомогательные широты которые имеют приложения к специальным задачам геодезии, геофизики и теории картографических проекций:

• Геоцентрическая широта
• Параметрическая (или приведенная) широта
• Исправление широты
• Аутальная широта
• Конформная широта
• Изометрическая широта

Определения, приведенные в данном разделе все относятся к местоположению на ссылке эллипсоида, но первые два вспомогательных широты, как и геодезической широты, может быть расширен, чтобы определить трехмерную географическая система координат как обсуждалось ниже. Остальные широты таким образом не используются; Они используются Только в качестве промежуточных конструкций в картографических проекциях эллипсоида отсчета на плоскость или при расчетах геодезических на эллипсоиде. Их числовые значения не представляют интереса. Например, никому не нужно вычислять подлинную широту Эйфелевой башни.

Приведенные ниже выражения дают вспомогательные широты в терминах геодезической широты, большой полуоси, а, и эксцентриситет, е. (Обратные см. ниже.) Приведены формы, помимо вариантов обозначений, те, которые содержатся в стандартном справочнике картографических проекций, а именно "Картографические проекции: рабочее руководство" Дж. П. Снайдера.^[9] Выводы этих выражений можно найти у Адамса.^[10] и онлайн-публикации Осборна^[5] и Рапп.^[6]

Геоцентрическая широта

Определение геодезической широты (φ) и геоцентрической широты (θ).

В геоцентрическая широта - угол между экваториальной плоскостью и радиусом от центра до точки на поверхности. Связь геоцентрической широты (θ) и геодезической широты (φ) выводится в приведенных выше ссылках как

${displaystyle heta (phi) = an ^ {- 1} left (left (1-e ^ {2} ight) an phi ight) = an ^ {- 1} left ((1-f) ^ {2} an phi ight) ,.}$

Геодезическая и геоцентрическая широты равны на экваторе и на полюсах, но на других широтах они отличаются на несколько угловых минут. Принимая значение квадрата эксцентриситета равным 0,0067 (это зависит от выбора эллипсоида), максимальная разница ${displaystyle phi {-} heta}$ может быть показано, что это около 11,5 угловых минут на геодезической широте примерно 45 ° 6 ′.^[c]

Параметрическая (или приведенная) широта

Определение параметрической широты (β) на эллипсоиде.

В параметрический или же уменьшенная широта, β, определяется радиусом, проведенным от центра эллипсоида до этой точки Q на окружающей сфере (радиуса а), которая представляет собой параллельную оси Земли проекцию точки п на эллипсоиде на широте φ. Его представил Лежандр^[11] и Бессель^[12] который решил задачи для геодезических на эллипсоиде, преобразовав их в эквивалентную задачу для сферических геодезических, используя эту меньшую широту. Обозначения Бесселя, ты(φ), также используется в современной литературе. Параметрическая широта связана с геодезической широтой:^[5][6]

${displaystyle eta (phi) = an ^ {- 1} left ({sqrt {1-e ^ {2}}} an phi ight) = an ^ {- 1} left ((1-f) an phi ight)}$

Альтернативное название происходит от параметризации уравнения эллипса, описывающего меридиональное сечение. В декартовых координатах п, расстояние от малой оси и z, расстояние над экваториальной плоскостью, уравнение эллипс является:

${displaystyle {frac {p ^ {2}} {a ^ {2}}} + {frac {z ^ {2}} {b ^ {2}}} = 1 ,.}$

Декартовы координаты точки параметризуются как

${displaystyle p = acos eta ,, qquad z = bsin eta,;}$

Кэли предложил термин параметрическая широта из-за формы этих уравнений.^[13]

Параметрическая широта не используется в теории картографических проекций. Его наиболее важное приложение - в теории эллипсоидных геодезических (Винсенти, Карни^[14]).

Исправление широты

В исправление широты, μ, - меридианное расстояние, масштабированное так, чтобы его значение на полюсах было равно 90 градусам или π/2 радианы:

${displaystyle mu (phi) = {frac {pi} {2}} {frac {m (phi)} {m_ {mathrm {p}}}}}$

где меридиональное расстояние от экватора до широты φ есть (см. Дуга меридиана )

${displaystyle m (phi) = aleft (1-e ^ {2} ight) int _ {0} ^ {phi} left (1-e ^ {2} sin ^ {2} phi 'ight) ^ {- {frac {3} {2}}}, dphi ',,}$

и длина меридионального квадранта от экватора до полюса ( полярное расстояние ) является

${displaystyle m_ {mathrm {p}} = mleft ({frac {pi} {2}} ight) ,.}$

Использование выпрямляющей широты для определения широты на сфере радиуса

${displaystyle R = {frac {2m_ {mathrm {p}}} {pi}}}$

определяет проекцию эллипсоида на сферу, так что все меридианы имеют истинную длину и одинаковый масштаб. Затем сферу можно спроецировать на плоскость с помощью равнопрямоугольная проекция для создания двойной проекции эллипсоида на плоскость, чтобы все меридианы имели истинную длину и единый масштаб меридиана. Примером использования выпрямляющей широты является эквидистантная коническая проекция. (Снайдер, Раздел 16).^[9] Выпрямляющая широта также имеет большое значение при строительстве Поперечная проекция Меркатора.

Аутальная широта

В аутентичный (По-гречески та же область ) широта, ξ, дает сохраняющую площадь преобразование в сферу.

${displaystyle xi (phi) = sin ^ {- 1} left ({frac {q (phi)} {q_ {mathrm {p}}}} ight)}$

куда

${displaystyle {egin {выровнен} q (phi) & = {frac {left (1-e ^ {2} ight) sin phi} {1-e ^ {2} sin ^ {2} phi}} - {frac { 1-e ^ {2}} {2e}} ln left ({frac {1-esin phi} {1 + esin phi}} ight) [2pt] & = {frac {left (1-e ^ {2}) ight) sin phi} {1-e ^ {2} sin ^ {2} phi}} + {frac {1-e ^ {2}} {e}} anh ^ {- 1} (esin phi) end {выровнено }}}$

и

${displaystyle {egin {align} q_ {mathrm {p}} = qleft ({frac {pi} {2}} ight) & = 1- {frac {1-e ^ {2}} {2e}} ln left ( {frac {1-e} {1 + e}} ight) & = 1+ {frac {1-e ^ {2}} {e}} anh ^ {- 1} eend {выровнено}}}$

а радиус сферы принимается равным

${displaystyle R_ {q} = a {sqrt {frac {q_ {mathrm {p}}} {2}}} ,.}$

Примером использования аутентичной широты является Равноплощадочная коническая проекция Альберса.^[9]:§14

Конформная широта

В конформная широта, χ, дает сохраняющий угол (конформный ) преобразование в сферу.

${displaystyle {egin {align} chi (phi) & = 2 an ^ {- 1} left [left ({frac {1 + sin phi} {1-sin phi}} ight) left »({frac {1-esin phi) } {1 + esin phi}} ight) ^ {e} ight] ^ {frac {1} {2}} - {frac {pi} {2}} [2pt] & = 2 an ^ {- 1} left [левый ({frac {phi} {2}} + {frac {pi} {4}} ight) левый ({frac {1-esin phi} {1 + esin phi}} полет) ^ {frac {e} {2}} ight] - {frac {pi} {2}} [2pt] & = an ^ {- 1} left [sinh left (sinh ^ {- 1} (an phi) -e anh ^ {- 1 } (esin phi) ight) ight] & = OperatorName {gd} left [operatorname {gd} ^ {- 1} (phi) -e anh ^ {- 1} (esin phi) ight] end {выровнено}}}$

куда gd (Икс) это Функция Гудермана. (Смотрите также Проекция Меркатора.)

Конформная широта определяет преобразование эллипсоида в сферу произвольный радиус такой, чтобы угол пересечения между любыми двумя линиями на эллипсоиде был таким же, как и соответствующий угол на сфере (так, чтобы форма маленький элементы хорошо сохранились). Дальнейшее конформное преобразование сферы в плоскость дает двойную конформную проекцию эллипсоида на плоскость. Это не единственный способ создания такой конформной проекции. Например, «точная» версия Поперечная проекция Меркатора на эллипсоиде нет двойной проекции. (Однако это подразумевает обобщение конформной широты на комплексную плоскость).

Изометрическая широта

В изометрическая широта, ψ, используется при разработке эллипсоидальных версий нормального Проекция Меркатора и Поперечная проекция Меркатора. Название «изометрический» происходит от того факта, что в любой точке эллипсоида равные приращения ψ и долгота λ вызывают смещения на равные расстояния по меридианам и параллелям соответственно. В сетка определяется линиями постоянного ψ и постоянный λ, делит поверхность эллипсоида на сетку квадратов (разного размера). Изометрическая широта равна нулю на экваторе, но быстро отклоняется от геодезической широты, стремясь к бесконечности на полюсах. Условные обозначения даны у Снайдера (стр. 15):^[9]

${displaystyle {egin {align} psi (phi) & = ln left [левый ({frac {pi} {4}} + {frac {phi} {2}} ight) ight]] + {frac {e} {2 }} ln left [{frac {1-esin phi} {1 + esin phi}} ight] & = sinh ^ {- 1} (an phi) -e anh ^ {- 1} (esin phi) & = имя оператора {gd} ^ {- 1} (phi) -e anh ^ {- 1} (esin phi) .end {выровнено}}}$

Для нормальный Проекция Меркатора (на эллипсоиде) эта функция определяет расстояние между параллелями: если длина экватора на проекции равна E (единицы длины или пиксели), затем расстояние, у, параллели широты φ от экватора

${displaystyle y (phi) = {frac {E} {2pi}} psi (phi) ,.}$

Изометрическая широта ψ тесно связан с конформной широтой χ:

${displaystyle psi (phi) = имя оператора {gd} ^ {- 1} chi (phi) ,.}$

Обратные формулы и ряды

Формулы в предыдущих разделах дают дополнительную широту в терминах геодезической широты. Выражения для геоцентрической и параметрической широт можно инвертировать напрямую, но это невозможно в четырех оставшихся случаях: выпрямляющей, аутентичной, конформной и изометрической широтах. Есть два способа действовать. Первый - это численное обращение определяющего уравнения для каждого отдельного значения дополнительной широты. Доступные методы: итерация с фиксированной точкой и Ньютон – Рафсон поиск корня. Другой, более полезный подход состоит в том, чтобы выразить вспомогательную широту в виде ряда с точки зрения геодезической широты, а затем инвертировать ряд методом Возврат Лагранжа. Такие ряды представлены Адамсом, который использует разложения в ряд Тейлора и дает коэффициенты в терминах эксцентриситета.^[10] Осборн^[5] выводит ряды в произвольном порядке с помощью пакета компьютерной алгебры Maxima^[15] и выражает коэффициенты как с точки зрения эксцентриситета, так и сглаживания. Метод серий не применим к изометрической широте, и необходимо использовать конформную широту на промежуточном этапе.

Численное сравнение вспомогательных широт

График справа показывает разницу между геодезической широтой и вспомогательными широтами, кроме изометрической широты (которая расходится до бесконечности на полюсах) для случая эллипсоида WGS84. На графике показаны различия в угловых минутах. В Северном полушарии (положительные широты), θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ φ; в Южном полушарии (отрицательные широты) неравенства обратные, с равенством на экваторе и полюсах. Хотя график кажется симметричным относительно 45 °, минимумы кривых на самом деле лежат между 45 ° 2 'и 45 ° 6'. Некоторые репрезентативные данные приведены в таблице ниже. Конформные и геоцентрические широты почти неотличимы, и этот факт использовался во времена ручных калькуляторов для ускорения построения картографических проекций.^[9]:108

В первую очередь в сплющивании жвспомогательные широты можно выразить какζ = φ − Cf грех 2φгде постоянная C принимает значения [¹⁄₂, ​²⁄₃, ​³⁄₄, 1, 1] дляζ = [β, ξ, μ, χ, θ].

Широта и системы координат

Геодезическая широта, или любой из вспомогательных широт, определенных на эллипсоид, представляет собой с долготой двумерный системы координат на этом эллипсоиде. Чтобы определить положение произвольной точки, необходимо расширить такую ​​систему координат до трех измерений. Таким образом используются три широты: геодезическая, геоцентрическая и параметрическая широты используются в геодезических координатах, сферических полярных координатах и ​​эллипсоидальных координатах соответственно.

Геодезические координаты

Геодезические координаты П(ɸ,λ,час)

В произвольной точке п рассмотрите линию PN который перпендикулярен эллипсоиду отсчета. Геодезические координаты П(ɸ,λ,час) широта и долгота точки N на эллипсоиде и расстоянии PN. Эта высота отличается от высоты над геоидом или от базовой высоты, например, над средним уровнем моря в указанном месте. Направление PN также будет отличаться от направления вертикального отвеса. Соотношение этих разных высот требует знания формы геоида, а также гравитационного поля Земли.

Сферические полярные координаты

Геоцентрическая координата, связанная со сферическими полярными координатами П(р,θ′,λ)

Геоцентрическая широта θ дополнение к полярному углу θ ′ в обычных сферические полярные координаты в котором координаты точки П(р,θ′,λ) куда р это расстояние п из центра О, θ ′ - угол между радиус-вектором и полярной осью, а λ долгота. Поскольку нормаль в общей точке эллипсоида не проходит через центр, ясно, что точки П' на нормали, которые имеют одинаковую геодезическую широту, будут иметь разные геоцентрические широты. Сферические полярные системы координат используются при анализе гравитационного поля.

Эллипсоидальные координаты

Эллипсоидальные координаты П(ты,β,λ)

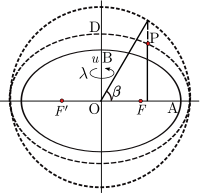
Параметрическая широта также может быть расширена до трехмерной системы координат. Для точки п не на эллипсоид (полуоси OA и OB) построить вспомогательный эллипсоид, который является конфокальным (те же фокусы F, F ′) со справочным эллипсоидом: необходимо, чтобы изделие ае большой полуоси и эксцентриситета одинаковы для обоих эллипсоидов. Позволять ты - малая полуось (OD) вспомогательного эллипсоида. Далее пусть β быть параметрической широтой п на вспомогательном эллипсоиде. Набор (ты,β,λ) определить координаты эллипсоида.^[4]:§4.2.2 Эти координаты являются естественным выбором в моделях гравитационного поля для вращающегося эллипсоидального тела.

Координатные преобразования

Связи между указанными выше системами координат, а также декартовыми координатами здесь не приводятся. Преобразование между геодезическими и декартовыми координатами можно найти в Преобразование географических координат. Соотношение декартовых и сферических поляр дано в Сферическая система координат. Связь декартовых и эллипсоидальных координат обсуждается в Торже.^[4]

Астрономическая широта

Астрономическая широта (Φ) - угол между плоскостью экватора и истинной вертикальное направление в точке на поверхности. Истинная вертикаль, направление отвес, также направление силы тяжести (результат гравитационное ускорение (массовый) и центробежное ускорение ) на этой широте.^[4] Астрономическая широта рассчитывается по углам, измеренным между зенит и звезды, чьи склонение точно известно.

В общем случае истинная вертикаль в точке на поверхности не совпадает точно ни с нормалью к эллипсоиду или нормалью к геоиду. Угол между астрономической и геодезической нормалями называется вертикальное отклонение и обычно составляет несколько угловых секунд, но это важно в геодезии.^[4][16] Причина, по которой он отличается от нормали к геоиду, заключается в том, что геоид представляет собой идеализированную теоретическую форму «на среднем уровне моря». Точки на реальной поверхности земли обычно находятся выше или ниже этой идеализированной поверхности геоида, и здесь истинная вертикаль может незначительно отличаться. Кроме того, на истинную вертикаль в точке в определенное время влияют приливные силы, которые усредняет теоретический геоид.

Астрономическую широту не следует путать с склонение, координата астрономы аналогичным образом используйте для указания углового положения звезд к северу / югу от небесный экватор (видеть экваториальные координаты ), ни с эклиптическая широта, координата, которую астрономы используют для определения углового положения звезд к северу / югу от эклиптика (видеть эклиптические координаты ).

Смотрите также

Рекомендации

Сноски

Цитаты

внешняя ссылка

• Сервер имен GEONets, доступ к Национальное агентство геопространственной разведки (NGA) база данных иностранных географических названий объектов.
• Ресурсы для определения вашей широты и долготы
• Преобразование десятичных градусов в градусы, минуты, секунды - Информация о десятичном для шестидесятеричный преобразование
• Преобразование десятичных градусов в градусы, минуты, секунды
• Расчет расстояния на основе широты и долготы - Версия JavaScript
• Обзор широты XVI века
• Определение широты Фрэнсисом Дрейком на побережье Калифорнии в 1579 году