Список картографических проекций - List of map projections

Это краткое изложение картографические проекции у которых есть собственные статьи в Википедии или другие примечательный. Поскольку количество возможных картографических проекций не ограничено,^[1] исчерпывающего списка быть не может.

Таблица прогнозов

Проекция	Изображение	Тип	Характеристики	Создатель	Год	Примечания
Равнопрямоугольный = эквидистантный цилиндрический = прямоугольный = la carte parallélogrammatique		Цилиндрический	Равноудаленный	Маринус Тирский	0120 c. 120	Самая простая геометрия; расстояния по меридианам сохраняются. Тарелка carrée: частный случай, когда экватор является стандартной параллелью.
Кассини = Кассини – Солднер		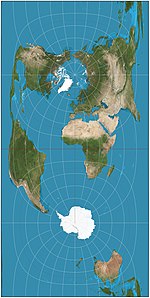Цилиндрический	Равноудаленный	Сезар-Франсуа Кассини де Тюри	1745	Поперечный эквидистантной проекции; расстояния по центральному меридиану сохраняются. Расстояния, перпендикулярные центральному меридиану, сохраняются.
Меркатор = Райт		Цилиндрический	Конформный	Герард Меркатор	1569	Линии постоянного пеленга (румба) прямые, что облегчает навигацию. Области увеличиваются с широтой, становясь настолько экстремальными, что на карте не отображаются полюса.
Web Mercator		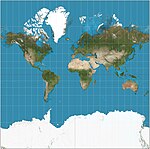Цилиндрический	Компромисс	Google	2005	Вариант Меркатор который игнорирует эллиптичность Земли для быстрых вычислений и обрезает широту до ~ 85,05 ° для квадратного представления. Фактически стандарт для картографических веб-приложений.
Гаусс – Крюгер = Конформный по Гауссу = (эллипсоидальная) поперечная проекция Меркатора		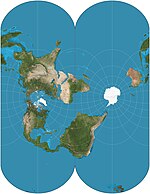Цилиндрический	Конформный	Карл Фридрих Гаусс Иоганн Генрих Луи Крюгер	1822	Эта поперечная эллипсоидальная форма Меркатора конечна, в отличие от экваториальной формы Меркатора. Формирует основу Универсальная поперечная система координат Меркатора.
Руссиль косой стереографический				Анри Руссиль	1922
Косая проекция Меркатора по Хотину		Цилиндрический	Конформный	М. Розенмунд, Дж. Лаборд, Мартин Хотин	1903
Галл стереографический		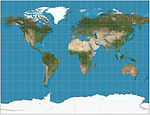Цилиндрический	Компромисс	Джеймс Галл	1855	Предназначен для напоминания Меркатора, но с отображением полюсов. Стандартные параллели под углом 45 ° с.ш.
Миллер = Миллер цилиндрический		Цилиндрический	Компромисс	Осборн Мейтленд Миллер	1942	Он призван напоминать Меркатор, но с одновременным отображением полюсов.
Ламберта цилиндрическая равновеликая		Цилиндрический	Равноплощадь	Иоганн Генрих Ламберт	1772	Стандартная параллель на экваторе. Соотношение сторон π (3.14). Базовая проекция цилиндрический равновеликий семья.
Берманн		Цилиндрический	Равноплощадь	Вальтер Берманн	1910	Горизонтально сжатый вариант равновеликой площади Ламберта. Имеет стандартные параллели на 30 ° с.ш. и соотношение сторон 2,36.
Хобо – Дайер		Цилиндрический	Равноплощадь	Мик Дайер	2002	Горизонтально сжатый вариант равновеликой площади Ламберта. Очень похожи выступы Тристана Эдвардса и Смита с равной поверхностью (= прямоугольной формы Крастера) со стандартными параллелями примерно на 37 ° с.ш. Соотношение сторон ~ 2,0.
Галл – Питерс = Галл орфографический = Питерс		Цилиндрический	Равноплощадь	Джеймс Галл (Арно Петерс )	1855	Горизонтально сжатый вариант равновеликой площади Ламберта. Стандартные параллели под углом 45 ° с.ш. Соотношение сторон ~ 1,6. Похожая проекция Бальтазарта со стандартными параллелями на 50 ° с / ю.
Центральный цилиндрический		Цилиндрический	Перспектива	(неизвестный)	1850 c. 1850	Практически не используется в картографии из-за сильного полярного искажения, но популярен в панорамная фотография, особенно для архитектурных сцен.
Синусоидальный = Сансон – Флемстид = Равновеликий Меркатор		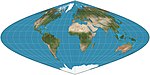Псевдоцилиндрический	Равноплоскостный, равноудаленный	(Несколько; первое неизвестно)	1600 c. 1600	Меридианы - синусоиды; параллели расположены на одинаковом расстоянии. Соотношение сторон 2: 1. Расстояния по параллелям сохраняются.
Mollweide = эллиптическая = Бабине = гомологичный		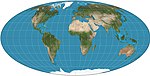Псевдоцилиндрический	Равноплощадь	Карл Брандан Моллвейде	1805	Меридианы - это эллипсы.
Эккерт II		Псевдоцилиндрический	Равноплощадь	Макс Эккерт-Грайфендорф	1906
Эккерт IV		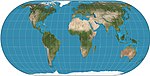Псевдоцилиндрический	Равноплощадь	Макс Эккерт-Грайфендорф	1906	Параллели не равны по размеру и масштабу; внешние меридианы - полукруги; остальные меридианы - полуэллипсы.
Эккерт В.И.		Псевдоцилиндрический	Равноплощадь	Макс Эккерт-Грайфендорф	1906	Параллели неравны по размеру и масштабу; меридианы - это полупериодные синусоиды.
Ортелиус овальный		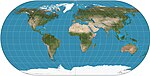Псевдоцилиндрический	Компромисс	Баттиста Аньезе	1540	Меридианы круглые.[2]
Гуд гомолозин		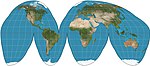Псевдоцилиндрический	Равноплощадь	Джон Пол Гуд	1923	Гибрид синусоидальной проекции и проекции Моллвейда. Обычно используется в прерывистой форме.
Каврайский VII		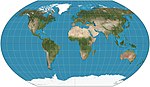Псевдоцилиндрический	Компромисс	Каврайский Владимир Васильевич	1939	Равномерно расположенные параллели. Эквивалентно Wagner VI, сжатому по горизонтали в раз ${ displaystyle { sqrt {3}} / {2}}$.
Робинсон		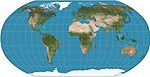Псевдоцилиндрический	Компромисс	Артур Х. Робинсон	1963	Вычислено путем интерполяции табличных значений. Используется Rand McNally с момента создания и используется NGS в 1988–1998 гг.
Равная Земля		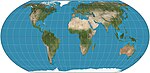Псевдоцилиндрический	Равноплощадь	Боян Шаврич, Том Паттерсон, Бернхард Дженни	2018	Вдохновлен проекцией Робинсона, но сохраняет относительный размер областей.
Естественная Земля		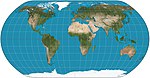Псевдоцилиндрический	Компромисс	Том Паттерсон	2011	Вычислено путем интерполяции табличных значений.
Тоблер гиперэллиптический		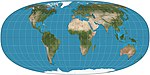Псевдоцилиндрический	Равноплощадь	Уолдо Р. Тоблер	1973	Семейство картографических проекций, которое включает в качестве особых случаев проекцию Моллвейда, проекцию Коллиньона и различные цилиндрические равновеликие проекции.
Вагнер В.И.		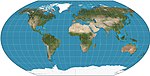Псевдоцилиндрический	Компромисс	К. Х. Вагнер	1932	Эквивалент Каврайского VII, сжатый по вертикали в раз ${ displaystyle { sqrt {3}} / {2}}$.
Collignon		Псевдоцилиндрический	Равноплощадь	Эдуард Коллиньон	1865 c. 1865	В зависимости от конфигурации проекция также может отображать сферу в виде одного ромба или пары квадратов.
HEALPix		Псевдоцилиндрический	Равноплощадь	Кшиштоф М. Горски	1997	Гибрид Коллиньона + Ламберта цилиндрической равноплоской.
Боггс эвморфический		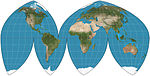Псевдоцилиндрический	Равноплощадь	Сэмюэл Уиттемор Боггс	1929	Равноплощадочная проекция, полученная в результате усреднения синусоидального сигнала и сигнала Моллвейда у-координаты и тем самым ограничивая Икс координировать.
Craster параболический = Путниньш P4		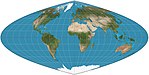Псевдоцилиндрический	Равноплощадь	Джон Крастер	1929	Меридианы - это параболы. Стандартные параллели на 36 ° 46′N / S; параллели неравны по интервалу и масштабу; Соотношение 2: 1.
Плоскополюсная квартика Макбрайда – Томаса = Макбрайд – Томас №4		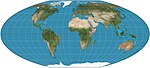Псевдоцилиндрический	Равноплощадь	Феликс В. Макбрайд, Пол Томас	1949	Стандартные параллели на 33 ° 45′N / S; параллели неравны по интервалу и масштабу; меридианы - кривые четвертого порядка. Без искажений только там, где стандартные параллели пересекают центральный меридиан.
Quartic authalic		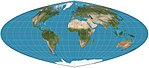Псевдоцилиндрический	Равноплощадь	Карл Симон Оскар Адамс	1937 1944	Параллели не равны по размеру и масштабу. Никаких искажений вдоль экватора. Меридианы - это кривые четвертого порядка.
Времена		Псевдоцилиндрический	Компромисс	Джон Мьюир	1965	Стандартные параллели 45 ° с / ю. Параллели на основе стереографики Галла, но с изогнутыми меридианами. Разработано для Bartholomew Ltd., The Times Atlas.
Локсимутал		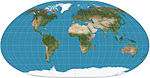Псевдоцилиндрический	Компромисс	Карл Симон Уолдо Р. Тоблер	1935 1966	От назначенного центра линии постоянного направления (линии румба / локсодромы) прямые и имеют правильную длину. Обычно асимметричный относительно экватора.
Айтофф		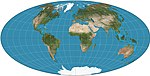Псевдоазимутал	Компромисс	Дэвид А. Айтофф	1889	Растяжка модифицированной экваториальной азимутальной эквидистантной карты. Граница - эллипс 2: 1. В значительной степени вытеснен Hammer.
Молоток = Хаммер – Айтофф вариации: Бриземейстер; Скандинавский		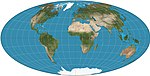Псевдоазимутал	Равноплощадь	Эрнст Хаммер	1892	Изменено с азимутальной экваториальной карты равноплощади. Граница - эллипс 2: 1. Варианты - наклонные версии с центром на 45 ° с.ш.
Strebe 1995		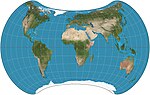Псевдоазимутал	Равноплощадь	Даниэль «даан» Стребе	1994	Сформулировано с использованием других картографических проекций равной площади в качестве преобразований.
Винкель трипель		Псевдоазимутал	Компромисс	Освальд Винкель	1921	Среднее арифметическое значение равнопрямоугольная проекция и Проекция Айтоффа. Стандартная мировая проекция для NGS с 1998 года.
Ван дер Гринтен		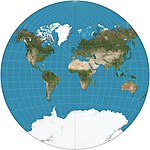Другой	Компромисс	Альфонс Дж. Ван дер Гринтен	1904	Граница - круг. Все параллели и меридианы представляют собой дуги окружности. Обычно обрезается около 80 ° с.ш. Стандартная мировая проекция NGS в 1922–1988 гг.
Эквидистантный конический = простая коническая		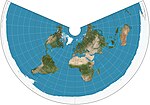Коническая	Равноудаленный	На основе Птолемей первая проекция	0100 c. 100	Расстояния по меридианам сохраняются, как и расстояния по одной или двум стандартным параллелям.[3]
Конформная коника Ламберта		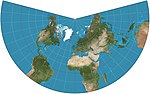Коническая	Конформный	Иоганн Генрих Ламберт	1772	Используется в авиационных картах.
Конический Альберса		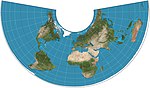Коническая	Равноплощадь	Генрих С. ​​Альберс	1805	Две стандартные параллели с низким уровнем искажений между ними.
Вернер		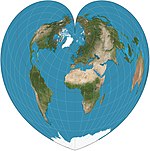Псевдоконический	Равноплоскостный, равноудаленный	Иоганнес Стабиус	1500 c. 1500	Параллели представляют собой концентрические дуги окружности, расположенные на одинаковом расстоянии друг от друга. Расстояния от Северный полюс верны, как и искривленные расстояния по параллелям и расстояния по центральному меридиану.
Bonne		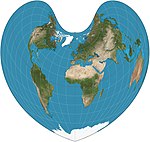Псевдоконический, сердцевидный	Равноплощадь	Бернард Сильванус	1511	Параллели - это концентрические дуги окружности, расположенные на равных расстояниях, и стандартные прямые. Внешний вид зависит от эталонной параллели. Общий случай как Вернера, так и синусоидального.
Боттомли		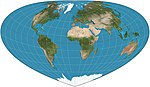Псевдоконический	Равноплощадь	Генри Боттомли	2003	Альтернатива выступу Бонне с более простой общей формой Параллели - это эллиптические дуги. Внешний вид зависит от эталонной параллели.
Американская поликоника		Псевдоконический	Компромисс	Фердинанд Рудольф Хасслер	1820 c. 1820	Расстояния по параллелям сохраняются, как и расстояния по центральному меридиану.
Прямоугольная поликоника		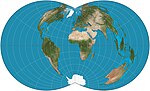Псевдоконический	Компромисс	Обследование побережья США	1853 c. 1853	Может быть выбрана широта и правильный масштаб. Параллели пересекаются с меридианами под прямым углом.
Широтно-равно-дифференциальная поликоника		Псевдоконический	Компромисс	Государственное бюро геодезии и картографии Китая	1963	Поликонический: параллели - это неконцентрические дуги окружностей.
Николози шаровидный		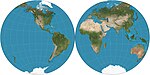Псевдоконический[4]	Компромисс	Абу Райнан аль-Бируни; заново изобретен Джованни Баттиста Николози в 1660 году.[1]:14	1000 c. 1000
Азимутальный эквидистант = Postel = зенитный эквидистант		Азимутальный	Равноудаленный	Абу Райнан аль-Бируни	1000 c. 1000	Расстояния от центра сохраняются. Используется как эмблема Организации Объединенных Наций, простирается до 60 ° южной широты.
Гномонический		Азимутальный	Гномонический	Фалес (возможно)	c. 580 г. до н.э.	Все большие круги переходят в прямые линии. Искажение вдали от центра. Показывает менее одного полушария.
Азимутальный равновеликий Ламберт		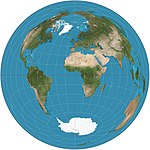Азимутальный	Равноплощадь	Иоганн Генрих Ламберт	1772	Расстояние по прямой между центральной точкой на карте и любой другой точкой такое же, как и расстояние по прямой в 3D через земной шар между двумя точками.
Стереографический		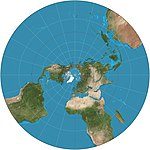Азимутальный	Конформный	Hipparchos *	c. 200 г. до н.э.	Карта бесконечна по размеру, внешнее полушарие сильно раздувается, поэтому ее часто используют как два полушария. Преобразует все маленькие кружки в кружки, что полезно при картографировании планет для сохранения формы кратеров.
Орфографический		Азимутальный	Перспектива	Hipparchos *	c. 200 г. до н.э.	Вид с бесконечного расстояния.
Вертикальная перспектива		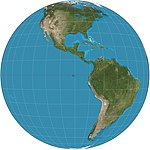Азимутальный	Перспектива	Маттиас Сейттер *	1740	Вид с конечного расстояния. Может отображать только полушарие.
Двухточечный эквидистант		Азимутальный	Равноудаленный	Ганс Маурер	1919	Две «контрольные точки» можно выбрать практически произвольно. Два расстояния по прямой от любой точки на карте до двух контрольных точек верны.
Пирс квинкунсиал		Другой	Конформный	Чарльз Сандерс Пирс	1879	Тесселяции. Может быть выложен плиткой непрерывно на плоскости с согласованием пересечений краев, за исключением четырех особых точек на плитку.
Проекция полусферы в квадрате Гую		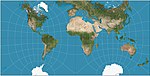Другой	Конформный	Эмиль Гю	1887	Тесселяции.
Проекция полусферы в квадрате Адамса		Другой	Конформный	Оскар Шерман Адамс	1925
Конформный мир Ли на тетраэдре		Многогранник	Конформный	Л. П. Ли	1965	Проецирует глобус на правильный тетраэдр. Тесселяции.
Проекция октанта		Многогранник	Компромисс	Леонардо да Винчи	1514	Проецирует земной шар на восемь октантов (Треугольники Рило ) без меридианов и параллелей.
Карта бабочек Кэхилла		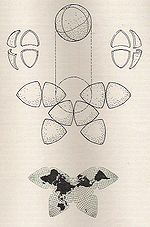Многогранник	Компромисс	Бернард Джозеф Станислав Кэхилл	1909	Проецирует земной шар на октаэдр с симметричными компонентами и смежными массивами суши, которые могут отображаться в различных компоновках.
Проекция Кэхилла – Киза		Многогранник	Компромисс	Джин Киз	1975	Проецирует земной шар на усеченный октаэдр с симметричными компонентами и прилегающими массами суши, которые могут отображаться в различных схемах.
Проекция бабочки Waterman		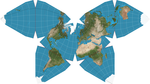Многогранник	Компромисс	Стив Уотерман	1996	Проецирует земной шар на усеченный октаэдр с симметричными компонентами и прилегающими массами суши, которые могут отображаться в различных схемах.
Четырехсторонний сферический куб		Многогранник	Равноплощадь	Ф. Кеннет Чан, Э. М. О'Нил	1973
Карта Dymaxion		Многогранник	Компромисс	Бакминстер Фуллер	1943	Также известна как проекция Фуллера.
Проекция AuthaGraph	Ссылка на файл	Многогранник	Компромисс	Хадзиме Нарукава	1999	Примерно равноплощадь. Тесселяции.
Мирияэдрические проекции		Многогранник	Равноплощадь	Ярке Й. ван Вейк	2008	Проецирует глобус на миаэдр: многогранник с очень большим количеством граней.[5][6]
Крейг ретроазимутал = Мекка		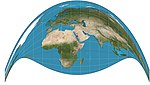Ретроазимутал	Компромисс	Джеймс Айрлэнд Крейг	1909
Молоток ретроазимутальный, передняя полусфера		Ретроазимутал		Эрнст Хаммер	1910
Молоток ретроазимутальный, задняя полусфера		Ретроазимутал		Эрнст Хаммер	1910
Литтроу		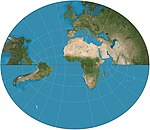Ретроазимутал	Конформный	Джозеф Иоганн Литтроу	1833	в экваториальном аспекте - полушарие, за исключением полюсов.
Армадилло		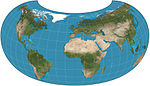Другой	Компромисс	Эрвин Райс	1943
GS50		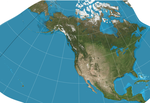Другой	Конформный	Джон П. Снайдер	1982	Разработан специально для минимизации искажений при отображении всех 50 Штаты США.
Вагнер VII = Хаммер-Вагнер		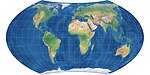Псевдоазимутал	Равноплощадь	К. Х. Вагнер	1941
Атлантида = Поперечный Mollweide		Псевдоцилиндрический	Равноплощадь	Иоанн Варфоломей	1948	Косая версия Моллвейде
Бертин = Бертен-Ривьер = Бертен 1953		Другой	Компромисс	Жак Бертен	1953	Проекция, в которой компромисс больше не является однородным, а вместо этого модифицируется для большей деформации океанов, чтобы добиться меньшей деформации континентов. Обычно используется для французских геополитических карт.[7]

* Первый известный популяризатор / пользователь, но не обязательно создатель.

Ключ

Тип проекции

Цилиндрический

В стандартном представлении они отображают меридианы с регулярным интервалом в вертикальные линии с одинаковым интервалом и параллели с горизонтальными линиями.

Псевдоцилиндрический

В стандартном представлении они отображают центральный меридиан и параллели в виде прямых линий. Остальные меридианы представляют собой кривые (или, возможно, прямые от полюса к экватору), равномерно расположенные вдоль параллелей.

Коническая

В стандартном представлении конические (или конические) проекции отображают меридианы как прямые линии, а параллели как дуги окружностей.

Псевдоконический

В стандартном представлении псевдоконические проекции представляют центральный меридиан в виде прямой линии, другие меридианы в виде сложных кривых и параллели в виде дуг окружности.

Азимутальный

В стандартном представлении азимутальные проекции отображают меридианы в виде прямых линий, а параллели - в виде полных концентрических окружностей. Они радиально-симметричны. В любой презентации (или аспекте) они сохраняют направления от центральной точки. Это означает, что большие круги, проходящие через центральную точку, представлены на карте прямыми линиями.

Псевдоазимутал

В стандартном представлении псевдоазимутальные проекции отображают экватор и центральный меридиан в виде перпендикулярных пересекающихся прямых линий. Они отображают параллели сложным кривым, отклоняющимся от экватора, и меридианы - сложным кривым, отклоняющимся к центральному меридиану. Перечислены здесь после псевдоцилиндрических, как в целом похожие на них по форме и назначению.

Другой

Обычно рассчитывается по формуле, а не на основе конкретной проекции

Многогранные карты

Многогранные карты можно сложить в многогранное приближение к сфере, используя определенную проекцию для отображения каждой грани с низким искажением.

Характеристики

Конформный

Сохраняет углы локально, подразумевая, что локальные формы не искажаются и что локальный масштаб постоянен во всех направлениях от любой выбранной точки.

Равноплощадь

Повсеместно сохраняется мера площади.

Компромисс

Ни конформная, ни равновеликая, а баланс, предназначенный для уменьшения общих искажений.

Равноудаленный

Все расстояния от одной (или двух) точек правильные. Другие равноудаленные свойства упомянуты в примечаниях.

Гномонический

Все большие круги - прямые.

Ретроазимутал

Направление к фиксированной точке B (по кратчайшему маршруту) соответствует направлению на карте от A до B.

Примечания

дальнейшее чтение

• Снайдер, Джон П. (1987). «Картографические проекции: Рабочее пособие». Картографические проекции - рабочее руководство (PDF). Профессиональная газета геологической службы США. 1395. Вашингтон, округ Колумбия: Типография правительства США. Дои:10.3133 / pp1395. Получено 2019-02-18.
• Снайдер, Джон П.; Voxland, Филип М. (1989). Альбом картографических проекций (PDF). Профессиональная газета геологической службы США. 1453. Вашингтон, округ Колумбия: Типография правительства США. Дои:10.3133 / pp1453. Получено 2019-02-18.