Азимутальная равновеликая проекция Ламберта - Википедия - Lambert azimuthal equal-area projection

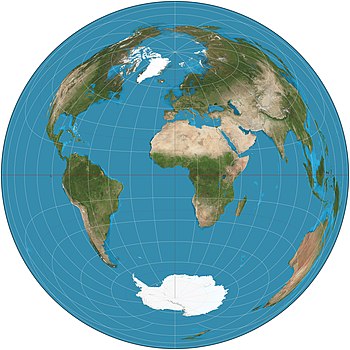
Азимутальная равновеликая проекция мира Ламберта. Центр - 0 ° N 0 ° E. Антипод - 0 ° N 180 ° E, около Кирибати в Тихий океан. Эта точка представлена всей круговой границей карты, и океан вокруг этой точки отображается вдоль всей границы.

Азимутальная равновеликая проекция Ламберта с Индикатриса Тиссо деформации.

В Азимутальная равновеликая проекция Ламберта является конкретным отображением сферы в диск. Он точно представляет площадь во всех регионах сферы, но это не совсем точно углы. Он назван в честь Швейцарский математик Иоганн Генрих Ламберт, который объявил об этом в 1772 году.^[1] «Зенитал» является синонимом «азимутального», проекция также известна как Зенитальная равновеликая проекция Ламберта.^[2]

Азимутальная проекция Ламберта используется как картографическая проекция в картография. Например, Национальный атлас США использует азимутальную равновеликую проекцию Ламберта для отображения информации в онлайн-приложении Map Maker,^[3] и Европейское агентство по окружающей среде рекомендует использовать его для европейских карт для статистического анализа и отображения.^[4] Он также используется в научных дисциплинах, таких как геология для построения ориентации линий в трехмерном пространстве. Этому построению помогает особый вид миллиметровая бумага называется Сеть Шмидта.^[5]

Определение

А поперечное сечение вид на сферу и касательную к ней плоскость на S. Каждая точка на сфере (кроме антипода) проецируется на плоскость по дуге окружности с центром в точке касания сферы и плоскости.

Чтобы определить азимутальную проекцию Ламберта, представьте себе плоскость, касательную к сфере в некоторой точке S на сфере. Позволять п быть любой точкой на сфере, кроме антипод из S. Позволять d быть расстоянием между S и п в трехмерном пространстве (нет расстояние по поверхности сферы). Тогда проекция отправляет п в точку П' на плоскости, которая находится на расстоянии d из S.

Чтобы сделать это более точным, есть уникальный круг с центром в S, проходя через п, и перпендикулярно плоскости. Он пересекает плоскость в двух точках; позволять п'Быть тем, кто ближе к п. Это прогнозируемая точка. Смотрите рисунок. Антипод S исключается из проекции, поскольку искомый круг не уникален. Случай S является вырожденным; S проецируется на себя по окружности радиуса 0.^[6]

Требуются явные формулы для проведения проекции на компьютер. Рассмотрим проекцию с центром в S = (0, 0, −1) на единичная сфера, который представляет собой набор точек (Икс, у, z) в трехмерном пространстве р³ такой, что Икс² + у² + z² = 1. В Декартовы координаты (Икс, у, z) на сфере и (Икс, Y) на плоскости проекция и обратная ей тогда описываются

{ displaystyle { begin {align} (X, Y) & = left ({ sqrt { frac {2} {1-z}}} , x, { sqrt { frac {2} {1}) -z}}} , y right), (x, y, z) & = left ({ sqrt {1 - { frac {X ^ {2} + Y ^ {2}} {4 }}}} , X, { sqrt {1 - { frac {X ^ {2} + Y ^ {2}} {4}}}} , Y, -1 + { frac {X ^ { 2} + Y ^ {2}} {2}} right). End {выравнивается}}}

В сферические координаты (φ, θ) на сфере (с φ то зенит и θ то азимут ) и полярные координаты (р, Θ) на диске карта и обратная ей задаются формулами ^[6]

{ Displaystyle { begin {выровнено} (R, Theta) & = left (2 cos { frac { varphi} {2}}, theta right), ( varphi, theta) & = left (2 arccos { frac {R} {2}}, Theta right). end {align}}}

В цилиндрические координаты (р, θ, z) на сфере и полярных координатах (р, Θ) на плоскости отображение и обратное ему задаются формулой

{ Displaystyle { begin {align} (R, Theta) & = left ({ sqrt {2 (1 + z)}}, theta right), (r, theta, z) & = left (R { sqrt {1 - { frac {R ^ {2}} {4}}}}, Theta, -1 + { frac {R ^ {2}} {2}} right ). end {выравнивается}}}

Проекцию можно центрировать в других точках и определять на сферах с радиусом, отличным от 1, используя аналогичные формулы.^[7]

Характеристики

Как определено в предыдущем разделе, азимутальная проекция Ламберта единичной сферы не определена в (0, 0, 1). Он отправляет остальную часть сферы в открытый диск радиуса 2 с центром в начале координат (0, 0) на плоскости. Он отправляет точку (0, 0, −1) в (0, 0), экватор z = 0 в круг радиуса √2 с центром в (0, 0), а нижнее полушарие z <0 на открытый диск, содержащийся в этом круге.

Проекция - это диффеоморфизм (а биекция то есть бесконечно дифференцируемый в обоих направлениях) между сферой (минус (0, 0, 1)) и открытым диском радиуса 2. Это сохраняющая площадь (равная площадь) карта, которую можно увидеть, вычислив элемент площади сферы при параметризации обратной проекции. В декартовых координатах это

{ Displaystyle dA = dX ; dY.}

Это означает, что измерение площади области на сфере равносильно измерению площади соответствующей области на диске.

С другой стороны, проекция не сохраняет угловые соотношения между кривыми на сфере. Никакое отображение между частью сферы и плоскостью не может сохранить и углы, и площади. (Если бы это было так, то это был бы местный изометрия и сохранит Гауссова кривизна; но сфера и диск имеют разную кривизну, поэтому это невозможно.) Тот факт, что плоские изображения не могут идеально отображать области сфер, является фундаментальной проблемой картографии.

Как следствие, области на сфере могут проецироваться на плоскость с сильно искаженными формами. Это искажение особенно заметно вдали от центра проекции (0, 0, -1). На практике проекция часто ограничивается полушарием с центром в этой точке; другое полушарие можно нанести на карту отдельно, используя вторую проекцию с центром в антиподе.

Приложения

Азимутальная проекция Ламберта изначально задумывалась как картографическая проекция равной площади. Теперь он также используется в таких дисциплинах, как геология для построения направленных данных следующим образом.

Направление в трехмерном пространстве соответствует линии, проходящей через начало координат. Набор всех таких линий сам по себе является пространством, называемым реальная проективная плоскость в математика. Каждая прямая, проходящая через начало координат, пересекает единичную сферу ровно в двух точках, одна из которых находится в нижней полусфере. z ≤ 0. (Горизонтальные линии пересекают экватор z = 0 в двух противоположных точках. Подразумевается, что противоположные точки на экваторе представляют собой одну линию. Видеть факторная топология.) Следовательно, направления в трехмерном пространстве соответствуют (почти идеально) точкам в нижней полусфере. Затем полусферу можно изобразить как диск радиуса √2 с помощью азимутальной проекции Ламберта.

Таким образом, азимутальная проекция Ламберта позволяет нам отображать направления в виде точек на диске. Благодаря свойству равноплоскости проекции можно интегрировать по областям реальной проективной плоскости (пространству направлений) путем интегрирования по соответствующим областям на диске. Это полезно для статистического анализа направленных данных,^[6] включая случайные жесткие вращение.^[8]

С помощью азимутальной проекции Ламберта можно построить не только линии, но и плоскости, проходящие через начало координат. Плоскость пересекает полусферу по дуге окружности, называемой след плоскости, которая спускается вниз до кривой (обычно некруглой) в диске. Можно построить эту кривую или заменить плоскость перпендикулярной ей линией, называемой столб, и вместо этого постройте эту линию. Когда несколько плоскостей строятся вместе, нанесение полюсов вместо трасс позволяет получить менее загроможденный график.

Исследователи в структурная геология использовать азимутальную проекцию Ламберта для построения кристаллографический топоры и грани, родословная и слоение в скалах, гладкие поверхности в недостатки, а также другие линейные и плоские объекты. В этом контексте проекция называется равновеликая полусферическая проекция. Существует также равноугловая полусферическая проекция, определяемая стереографическая проекция.^[6]

Обсуждение здесь акцентировалось на нижнем полушарии. z ≤ 0, но некоторые дисциплины предпочитают верхнее полушарие z ≥ 0.^[6] Действительно, любое полушарие можно использовать для записи линий, проходящих через начало координат в трехмерном пространстве.

Сравнение Азимутальная равновеликая проекция Ламберта и некоторые азимутальные проекции с центром на 90 ° с.ш. в том же масштабе, упорядоченные по высоте проекции в радиусах Земли. (нажмите для подробностей)

Анимированная проекция Ламберта

^{[нужна цитата ]}

Анимация проекции Ламберта. Каждая ячейка сетки сохраняет свою площадь на протяжении всего преобразования. В этой анимации точки на экваторе всегда остаются на

{ displaystyle z = 0}

самолет.

В этой анимированной проекции Ламберта южный полюс зафиксирован.

Позволять ${ displaystyle (и, phi)}$ быть двумя параметрами, для которых ${ Displaystyle -1 <и leq 1}$ и ${ Displaystyle 0 Leq phi <2 pi}$ . Позволять ${ displaystyle H}$ быть параметром «время» (равным высоте или вертикальной толщине оболочки в анимации). Если нарисовать равномерную прямолинейную сетку в ${ displaystyle (и, phi)}$ пространство, то любая точка в этой сетке преобразуется в точку ${ Displaystyle (х, у, г)}$ на сферической оболочке высотой ${ displaystyle H}$ согласно отображению

${ Displaystyle х = лямбда (и, ЧАС) соз ( фи)}$

${ Displaystyle у = лямбда (и, ЧАС) грех ( фи)}$

${ displaystyle z = { frac {Hu} {2}}}$

куда ${ displaystyle lambda (u, H) = { frac {1} {2}} { sqrt {(1-u) left [8-H ^ {2} (1-u) right]}} }$ . Каждый кадр в анимации соответствует параметрическому графику деформированной сетки при фиксированном значении высоты оболочки. ${ displaystyle H}$ (от 0 до 2). Физически, ${ displaystyle lambda}$ - растяжение (деформированная длина, деленная на начальную длину) бесконечно малой линии ${ displaystyle d phi}$ отрезки линии. Это сопоставление можно преобразовать в сопоставление, в котором южный полюс остается фиксированным, используя вместо этого ${ displaystyle z = { frac {H (1-u)} {2}}.}$

Независимо от значений ${ displaystyle (и, phi, H)}$ , якобиан этого сопоставления везде равен 1, показывая, что это действительно сопоставление одинаковой площади на протяжении всей анимации. Это обобщенное отображение включает проекцию Ламберта как частный случай, когда ${ displaystyle H = 0}$ .

Применение: это отображение может помочь в объяснении значения проекции Ламберта, показывая, что она «вскрывает» сферу на полюсе, превращая ее в диск без изменения области, заключенной в ячейках сетки.

Смотрите также

внешняя ссылка

Пояснения к преобразованию координат с диаграммами
СМИ, связанные с Азимутальная равновеликая проекция Ламберта в Wikimedia Commons

[mulcahy_lambert-1] Малкахи, Карен. «Азимуталь Ламберта равной площади». Городской университет Нью-Йорка. Получено 2007-03-30.

[2] Атлас мира The Times (1967), Бостон: Houghton Mifflin, Plate 3, et passim.

[3] «Картографические проекции: от сферической Земли к плоской карте». Министерство внутренних дел США. 2008-04-29. Архивировано из оригинал на 2009-05-07. Получено 2009-04-08.

[4] "Краткие материалы 1-го Европейского семинара по эталонным сеткам, Испра, 27-29 октября 2003 г." (PDF). Европейское агентство по окружающей среде. 2004-06-14. п. 6. Получено 2009-08-27.

[Ramsay1967-5] Рамзи (1967)

[borradaile2003-6] а ^б ^c ^d ^е Боррадейл (2003).

[7] «Руководство по геоматике 7, часть 2: Преобразование координат и преобразования, включая формулы» (PDF). Международная ассоциация производителей нефти и газа. Сентябрь 2016. Получено 2017-12-17.

[8] Браннон Р.М., «Поворот, отражение и смена кадра», 2018

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]