Эклиптика - Ecliptic

В эклиптика это самолет из Орбита Земли вокруг Солнца.[1][2][а] С точки зрения наблюдателя на Земле, движение Солнца вокруг небесная сфера в течение года прокладывает путь по эклиптике против фон из звезд.[3] Эклиптика - важный базовая плоскость и является основой эклиптическая система координат.
Видимое движение Солнца
Из-за движения Земли вокруг Земли – Луны. центр массы, видимый путь Солнца слегка колеблется с периодом около один месяц. Из-за дальнейшего возмущения другим планеты из Солнечная система, Земля – Луна барицентр слегка качается вокруг средней позиции сложным образом. На самом деле эклиптика - это видимый путь Солнца на протяжении всего пути. год.[4]
Поскольку Земле требуется один год, чтобы вращаться вокруг Солнца, видимое положение Солнца занимает один год, чтобы совершить полный оборот вокруг эклиптики. С чуть более чем 365 дней в году Солнце перемещается чуть менее чем на 1 ° к востоку.[5] ежедневно. Эта небольшая разница в положении Солнца по отношению к звездам заставляет любое конкретное пятно на поверхности Земли догонять (и стоять прямо к северу или югу от Солнца) каждый день примерно на четыре минуты позже, чем если бы Земля не вращалась по орбите; поэтому сутки на Земле длится 24 часа, а не примерно 23 часа 56 минут. звездный день. Опять же, это упрощение, основанное на гипотетической Земле, которая вращается с постоянной скоростью вокруг Солнца. Фактическая скорость, с которой Земля вращается вокруг Солнца, немного меняется в течение года, поэтому скорость, с которой кажется, что Солнце движется по эклиптике, также меняется. Например, Солнце находится к северу от небесного экватора примерно 185 дней в году и к югу от него примерно 180 дней.[6] Изменение орбитальной скорости составляет часть уравнение времени.[7]
Связь с небесным экватором

Потому что Ось вращения Земли не является перпендикуляр к его орбитальный самолет, Земли экваториальная плоскость не является копланарный с плоскостью эклиптики, но наклонен к ней на угол около 23,4 °, который известен как наклон эклиптики.[8] Если экватор спроектирован наружу на небесная сфера, формируя небесный экватор, он пересекает эклиптику в двух точках, известных как равноденствия. Солнце в своем видимом движении по эклиптике пересекает небесный экватор в этих точках, одна с юга на север, другая с севера на юг.[5] Переход с юга на север известен как весеннее равноденствие, также известный как первая точка Овна и восходящий узел эклиптики на небесном экваторе.[9] Переход с севера на юг - это осеннее равноденствие или же нисходящий узел.
Ориентация Ось земли и экватор не фиксируются в пространстве, а вращаются вокруг полюса эклиптики с периодом около 26000 лет, процесс, известный как лунно-солнечный прецессия, так как в основном это связано с гравитационным эффектом Луна и солнце на Экваториальная выпуклость Земли. Точно так же не фиксируется сама эклиптика. Гравитационный возмущения других органов Солнечная система вызывают гораздо меньшее движение плоскости орбиты Земли и, следовательно, эклиптики, известное как планетарный прецессия. Совместное действие этих двух движений называется Общее прецессия, и меняет положение равноденствий примерно на 50 угловые секунды (около 0,014 °) в год.[10]
Еще раз, это упрощение. Периодические движения Луна и кажущиеся периодические движения солнце (фактически Земли на своей орбите) вызывают кратковременные периодические колебания малой амплитуды оси Земли и, следовательно, небесного экватора, известного как нутация.[11]Это добавляет периодический компонент к положению равноденствий; положения небесного экватора и (весеннего) равноденствия с полностью обновленными прецессией и нутацией называются истинный экватор и равноденствие; позиции без нутации являются средний экватор и равноденствие.[12]
Наклон эклиптики
Наклон эклиптики - термин, используемый астрономами для обозначения наклона земной шар с экватор относительно эклиптики или Ось вращения Земли к перпендикуляр к эклиптике. Это около 23,4 ° и в настоящее время уменьшается на 0,013 градуса (47 угловых секунд) за сто лет из-за планетарных возмущения.[13]
Угловое значение наклона определяется путем наблюдения за движениями Земли и другие планеты на протяжении многих лет. Астрономы производят новые фундаментальные эфемериды как точность наблюдение улучшается и по мере понимания динамика увеличивается, и из этих эфемерид выводятся различные астрономические значения, включая наклон.
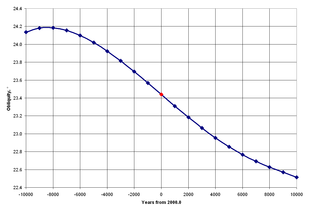
До 1983 года наклон для любой даты рассчитывался от работа Ньюкомба, который анализировал положение планет примерно до 1895 г .:
ε = 23° 27′ 08″.26 − 46″.845 Т − 0″.0059 Т2 + 0″.00181 Т3
куда ε наклон и Т является тропические века из B1900.0 к рассматриваемой дате.[15]
С 1984 г. Лаборатория реактивного движения серии DE компьютерных эфемерид взяли на себя основные эфемериды из Астрономический альманах. Наклон на основе DE200, который анализировал наблюдения с 1911 по 1979 год, был рассчитан:
ε = 23° 26′ 21″.45 − 46″.815 Т − 0″.0006 Т2 + 0″.00181 Т3
где в дальнейшем Т является Юлианские века из J2000.0.[16]
Основные эфемериды JPL постоянно обновляются. В Астрономический альманах на 2010 год указывает:[17]
ε = 23° 26′ 21″.406 − 46″.836769 Т − 0″.0001831 Т2 + 0″.00200340 Т3 − 0″.576×10−6 Т4 − 4″.34×10−8 Т5
Эти выражения для угла наклона предназначены для высокой точности за относительно короткий промежуток времени, возможно, несколько столетий.[18] Дж. Ласкар вычислил выражение на заказ Т10 хорош для 0″.04/ 1000 лет более 10 000 лет.[14]
Все эти выражения предназначены для иметь в виду наклонность, то есть без нутации экватора. В истинный или мгновенная наклонность включает нутацию.[19]
Самолет Солнечной системы
 |  |  |
| Вид сверху и сбоку плоскости эклиптики с планетами Меркурий, Венера, земной шар, и Марс. Большинство планет вращаются вокруг солнце почти в той же плоскости, в которой вращается Земля, - эклиптике. | Четыре планеты выстроились вдоль эклиптики в июле 2010 года, демонстрируя, как планеты вращаются вокруг Солнца почти в одной плоскости. Фотография сделана на закате, глядя на запад над Суракартой, Ява, Индонезия. | |
Большинство основных органов Солнечная система на орбите солнце почти в одном самолете. Вероятно, это связано с тем, как Солнечная система сформировалась из протопланетный диск. Вероятно, ближайшее текущее представление диска известно как неизменный самолет Солнечной системы. Орбита Земли, а значит, и эклиптика наклонены к неизменной плоскости чуть более чем на 1 °, орбита Юпитера находится в пределах чуть более 1 °.1⁄2° от нее, а все остальные большие планеты - в пределах примерно 6 °. Из-за этого большинство тел Солнечной системы выглядят очень близко к эклиптике в небе.
Неизменная плоскость определяется угловой момент всей Солнечной системы, по сути, векторная сумма всех орбитальный и вращающийся угловые моменты всех тел системы; более 60% всего приходится на орбиту Юпитера.[20] Эта сумма требует точного знания каждого объекта в системе, что делает ее несколько неопределенной величиной. Из-за неопределенности относительно точного местоположения неизменной плоскости и из-за того, что эклиптика хорошо определяется видимым движением солнце эклиптика используется в качестве базовой плоскости Солнечной системы как для точности, так и для удобства. Единственный недостаток использования эклиптики вместо неизменной плоскости состоит в том, что в геологических временных масштабах она будет двигаться против фиксированных контрольных точек на далеком фоне неба.[21][22]
Небесная опорная плоскость

Эклиптика образует одну из двух основных самолеты используется как ссылка для позиций на небесная сфера, другой - небесный экватор. Перпендикулярно эклиптике находятся эклиптические полюса Северный полюс эклиптики - это полюс к северу от экватора. Из двух фундаментальных плоскостей эклиптика ближе к неподвижности на фоне звезд, ее движение обусловлено планетарным прецессия приблизительно 1/100 небесного экватора.[23]
Сферические координаты, известные как эклиптическая долгота и широта или небесная долгота и широта, используются для определения положения тел на небесная сфера относительно эклиптики. Долгота положительно измеряется на восток[5] От 0 ° до 360 ° по эклиптике от точки весеннего равноденствия, в том же направлении, в котором солнце кажется движется. Широта измеряется перпендикулярно эклиптике, до + 90 ° к северу или -90 ° к югу до полюсов эклиптики, при этом сама эклиптика составляет 0 ° широты. Для полной сферической позиции также необходим параметр расстояния. Для разных объектов используются разные единицы расстояния. В рамках Солнечная система, астрономические единицы используются, а для объектов вблизи земной шар, Радиусы Земли или же километров используются. Соответствующий праворукий прямоугольная система координат также иногда используется; то Икс- ось направлена в сторону точки весеннего равноденствия, уось 90 ° на восток, а z- ось в сторону северный полюс эклиптики; то астрономическая единица это единица измерения. Символы эклиптических координат несколько стандартизированы; см. таблицу.[24]
| сферический | прямоугольный | |||
| долгота | широта | расстояние | ||
| геоцентрический | λ | β | Δ | |
| гелиоцентрический | л | б | р | Икс, у, z[примечание 1] |
| ||||
Эклиптические координаты удобны для указания положений Солнечная система объекты, как и большинство планет орбиты иметь маленький наклонности к эклиптике, и поэтому всегда появляются относительно близко к ней на небе. Поскольку орбита Земли, а следовательно, и эклиптика, очень мало перемещаются, это относительно фиксированная точка отсчета по отношению к звездам.

Из-за прецессионное движение равноденствия, эклиптические координаты объектов на небесной сфере непрерывно меняются. Для указания положения в эклиптических координатах необходимо указать конкретное равноденствие, то есть равноденствие определенной даты, известное как равноденствие. эпоха; координаты относятся к направлению равноденствия на эту дату. Например, Астрономический альманах[27] перечисляет гелиоцентрический положение Марс в 0ч Земное время, 4 января 2010 г. как: долгота 118 ° 09 '15 "0,8, широта + 1 ° 43' 16" 0,7, истинное гелиоцентрическое расстояние 1,6302454 а.е., среднее равноденствие и эклиптика даты. Это определяет среднее равноденствие от 4 января 2010 г. 0ч TT как указано выше, без добавления нутации.
Затмения
Поскольку орбита Луны наклонен к эклиптике всего на 5,145 °, а солнце всегда очень близко к эклиптике, затмения всегда возникают на нем или рядом с ним. Из-за наклона Луна с орбита, затмения случаются не каждый соединение и оппозиция Солнца и Луны, но только когда Луна находится около восходящий или нисходящий узел в то же время он находится в соединении (новый ) или оппозиция (полный ). Эклиптика названа так потому, что древние отмечали, что затмения происходят только тогда, когда Луна пересекает ее.[28]
Равноденствия и солнцестояния
| эклиптика | экваториальный | |
| долгота | прямое восхождение | |
| Мартовское равноденствие | 0° | 0ч |
| Июньское солнцестояние | 90° | 6ч |
| Сентябрьское равноденствие | 180° | 12ч |
| Декабрьское солнцестояние | 270° | 18ч |
Точные моменты равноденствия и солнцестояния времена, когда очевидное эклиптическая долгота (включая эффекты аберрация и нутация ) из солнце составляет 0 °, 90 °, 180 ° и 270 °. Потому что возмущения из Орбита Земли и аномалии календарь, даты их не фиксированы.[29]
В созвездиях

Эклиптика в настоящее время проходит через следующие созвездия:
Астрология
Эклиптика образует центр зодиак, небесный пояс шириной около 20 °, через который солнце, Луна, и планеты всегда кажется движущимся.[31] Традиционно этот регион делится на 12 приметы 30 ° долготы, каждая из которых приблизительно соответствует движению Солнца за один месяц.[32] В древние времена знаки соответствовали примерно 12 созвездиям, расположенным на эклиптике.[33]Эти знаки иногда все еще используются в современной терминологии. "Первая точка Овна "был назван, когда Мартовское равноденствие Солнце действительно было в созвездии Овен; с тех пор он переехал в Рыбы потому что прецессия равноденствий.[34]
Смотрите также
- Формирование и эволюция Солнечной системы
- Неизменная плоскость
- Протопланетный диск
- Система небесных координат
Примечания и ссылки
- ^ Собственно плоскость средней орбиты с небольшими усредненными отклонениями.
- ^ USNO Управление морского альманаха; Гидрографическое управление Великобритании, Управление морского альманаха HM (2008). Астрономический альманах за 2010 год. GPO. п. M5. ISBN 978-0-7077-4082-9.
- ^ «УРОВЕНЬ 5 Лексика и глоссарий терминов».
- ^ «Эклиптика: годовой путь Солнца на небесной сфере».
- ^ Управление морского альманаха военно-морской обсерватории США (1992). П. Кеннет Зайдельманн (ред.). Пояснительное приложение к астрономическому альманаху. Научные книги университета, Милл-Вэлли, Калифорния. ISBN 0-935702-68-7., п. 11
- ^ а б c Направления север и юг на небесной сфере в смысле к северу небесный полюс и к южному небесному полюсу. Восток является направление, в котором вращается Земля, Запад противоположно этому.
- ^ Астрономический альманах 2010, сек. C
- ^ Пояснительное приложение (1992), сек. 1,233
- ^ Пояснительное приложение (1992), стр. 733
- ^ Астрономический альманах 2010, п. М2 и М6
- ^ Пояснительное приложение (1992), сек. 1.322 и 3.21
- ^ Управление морского альманаха военно-морской обсерватории США; H.M. Управление морского альманаха (1961). Пояснительное приложение к астрономическим эфемеридам и американским эфемеридам и морскому альманаху. H.M. Канцелярский офис, Лондон., сек. 2C
- ^ Пояснительное приложение (1992), стр. 731 и 737
- ^ Шовене, Уильям (1906). Руководство по сферической и практической астрономии. я. J.B. Lippincott Co., Филадельфия., Изобразительное искусство. 365–367, с. 694–695, в Google Книги
- ^ а б Ласкар, Дж. (1986). «Секулярные термины классических планетных теорий, использующие результаты общей теории относительности». Bibcode:1986A & A ... 157 ... 59L. Цитировать журнал требует
| журнал =(помощь), таблица 8, в SAO / NASA ADS - ^ Пояснительное приложение (1961), сек. 2B
- ^ Военно-морская обсерватория США, Управление морского альманаха; H.M. Управление морского альманаха (1989). Астрономический альманах за 1990 год. Правительство США Типография. ISBN 0-11-886934-5., п. B18
- ^ Астрономический альманах 2010, п. B52
- ^ Ньюкомб, Саймон (1906). Компендиум сферической астрономии. MacMillan Co., Нью-Йорк., п. 226-227, в Google Книги
- ^ Миус, Жан (1991). Астрономические алгоритмы. Willmann-Bell, Inc., Ричмонд, Вирджиния. ISBN 0-943396-35-2., гл. 21 год
- ^ «Средняя плоскость (неизменная плоскость) Солнечной системы, проходящая через барицентр». 3 апреля 2009 г. Архивировано с оригинал 3 июня 2013 г.. Получено 10 апреля 2009. произведено с Витальяно, Альдо. «Солекс 10». Архивировано из оригинал (компьютерная программа) 29 апреля 2009 г.. Получено 10 апреля 2009.
- ^ Дэнби, J.M.A. (1988). Основы небесной механики. Willmann-Bell, Inc., Ричмонд, Вирджиния. раздел 9.1. ISBN 0-943396-20-4.
- ^ Рой, A.E. (1988). Орбитальное движение (третье изд.). Издательский институт Физики. раздел 5.3. ISBN 0-85274-229-0.
- ^ Монтенбрюк, Оливер (1989). Практические расчеты эфемерид. Springer-Verlag. ISBN 0-387-50704-3., сек 1.4
- ^ Пояснительное приложение (1961), сек. 2А
- ^ Пояснительное приложение (1961), сек. 1G
- ^ Дзиобек, Отто (1892). Математические теории движения планет. Register Publishing Co., Анн-Арбор, Мичиган., п. 294, в Google Книгах
- ^ Астрономический альманах 2010, п. E14
- ^ Болл, Роберт С. (1908). Трактат по сферической астрономии. Издательство Кембриджского университета. п.83.
- ^ Meeus (1991), гл. 26
- ^ Сервисс, Гаррет П. (1908). Астрономия невооруженным глазом. Harper & Brothers, Нью-Йорк и Лондон. стр.105, 106.
- ^ Брайант, Уолтер В. (1907). История астрономии. п. 3. ISBN 9781440057922.
- ^ Брайант (1907), стр. 4.
- ^ См., Например, Лео, Алан (1899). Астрология для всех. Л.Н. Фаулер и компания. п.8.
астрология.
- ^ Валладо, Дэвид А. (2001). Основы астродинамики и приложений (2-е изд.). Эль-Сегундо, Калифорния: Microcosm Press. п. 153. ISBN 1-881883-12-4.
внешняя ссылка
- Эклиптика: годовой путь Солнца на небесной сфере Департамент физики Даремского университета
- Сезоны и симулятор эклиптики Университет Небраски-Линкольн
- ИЗМЕРЕНИЕ НЕБО Краткое руководство по небесной сфере Джеймс Б. Калер, Иллинойский университет
- Времена года на Земле Военно-морская обсерватория США
- Основы - эклиптика, экватор и системы координат AstrologyClub.Org
- Kinoshita, H .; Аоки, С. (1983). «Определение эклиптики». Небесная механика. 31 (4): 329–338. Bibcode:1983CeMec..31..329K. Дои:10.1007 / BF01230290. S2CID 122913096.; сравнение определений Леверье, Ньюкома и Стэндиша.
