Осевая прецессия - Axial precession
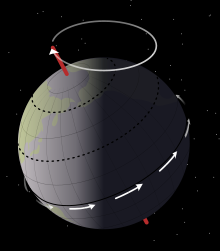
В астрономия, осевая прецессия это вызванное гравитацией, медленное и непрерывное изменение ориентации астрономического тела ось вращения. В частности, это может относиться к постепенному изменению ориентации земной шар Ось вращения России в цикле приблизительно 26 000 лет.[1] Это похоже на прецессию волчка, когда ось отслеживает пару шишки присоединились к их вершины. Термин «прецессия» обычно относится только к этой самой большой части движения; другие изменения в выравнивании оси Земли -нутация и полярное движение - намного меньше по величине.
Прецессию Земли исторически называли прецессия равноденствий, поскольку равноденствия двинулся на запад по эклиптика относительно фиксированные звезды, в отличие от годового движения солнце по эклиптике. Исторически,[2] открытие прецессии равноденствий на Западе обычно приписывают астроному II века до н.э. Гиппарх. С улучшением способности вычислять гравитационную силу между планетами в течение первой половины девятнадцатого века было признано, что сама эклиптика слегка перемещается, что и было названо планетарная прецессия, еще в 1863 г., а доминирующий компонент был назван лунно-солнечная прецессия.[3] Их комбинация получила название общая прецессия, вместо прецессии равноденствий.
Лунно-солнечная прецессия вызвана гравитационными силами Луна и Солнце на Земле экваториальная выпуклость, заставляя ось Земли двигаться относительно инерциальное пространство. Планетарная прецессия (опережение) происходит из-за малого угла между гравитационной силой других планет на Земле и ее орбитальной плоскостью (эклиптикой), в результате чего плоскость эклиптики слегка смещается относительно инерциального пространства. Лунно-солнечная прецессия примерно в 500 раз больше планетарной прецессии.[4] Помимо Луны и Солнца, другие планеты также вызывают небольшое движение оси Земли в инерциальном пространстве, что приводит к контрасту между лунно-солнечными и планетными терминами, вводящими в заблуждение, поэтому в 2006 году Международный астрономический союз рекомендовал переименовать доминирующий компонент в прецессия экватора, а второстепенный компонент переименовать прецессия эклиптики, но их сочетание по-прежнему называется общей прецессией.[5] Многие ссылки на старые термины существуют в публикациях, предшествующих изменению.
Номенклатура

"Прецессия " и "шествие "оба термина относятся к движение. «Прецессия» происходит от латинского прецедер («предшествовать, приходить раньше или раньше»), а «процессия» происходит от латинского процедура («идти вперед, идти вперед»). Обычно термин «процессия» используется для описания группы движущихся вперед объектов. Видно, что звезды, наблюдаемые с Земли, ежедневно движутся с востока на запад из-за земного дневное движение, и ежегодно, из-за обращения Земли вокруг Солнца. В то же время можно наблюдать, как звезды слегка предвосхищают такое движение со скоростью примерно 50 угловых секунд в год, явление, известное как «прецессия равноденствий».
При описании этого движения астрономы обычно сокращали термин до просто «прецессия». При описании причина Физики движения также использовали термин «прецессия», который привел к некоторой путанице между наблюдаемым явлением и его причиной, что имеет значение, потому что в астрономии одни прецессии реальны, а другие очевидны. Эта проблема еще больше усложняется тем фактом, что многие астрономы являются физиками или астрофизиками.
Термин «прецессия», используемый в астрономия в целом описывает наблюдаемую прецессию равноденствия (движущиеся звезды ретроградный по небу), тогда как термин «прецессия», используемый в физика, обычно описывает механический процесс.
Последствия
Прецессия оси Земли имеет ряд наблюдаемых эффектов. Во-первых, позиции юга и севера небесные полюса кажется, что они движутся по кругу на фоне неподвижных звезд, совершая один оборот примерно за 26000 лет. Таким образом, пока сегодня звезда Полярная звезда находится примерно на северном полюсе мира, это со временем изменится, и другие звезды станут "Полярная звезда ".[2] Примерно через 3200 лет звезда Гамма Цефеи в созвездии Цефея на этой позиции сменит Полярную звезду. Южный небесный полюс в настоящее время не имеет яркой звезды, чтобы обозначить его положение, но со временем прецессия также приведет к тому, что яркие звезды станут южные звезды. По мере смещения небесных полюсов происходит соответствующий постепенный сдвиг видимой ориентации всего звездного поля, если смотреть с определенного места на Земле.
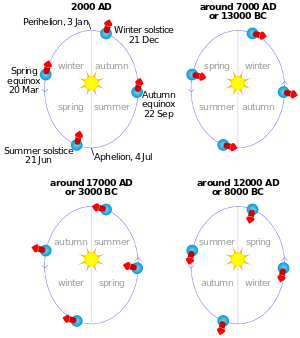
Во-вторых, положение Земли на ее орбите вокруг Солнца на солнцестояния, равноденствия, или другое время, определенное относительно сезонов, медленно меняется.[2] Например, предположим, что орбитальная позиция Земли отмечена во время летнего солнцестояния, когда осевой наклон указывает прямо на Солнце. Спустя один полный оборот, когда Солнце вернулось в то же видимое положение относительно фоновых звезд, осевой наклон Земли теперь не направлен прямо к Солнцу: из-за эффектов прецессии он находится немного "дальше". Другими словами, солнцестояние наступило немного ранее на орбите. Таким образом тропический год, измеряющий цикл времен года (например, время от солнцестояния до солнцестояния или от равноденствия до равноденствия), примерно на 20 минут короче, чем звездный год, который измеряется видимым положением Солнца относительно звезд. Примерно через 26 000 лет разница составляет целый год, так что положение сезонов относительно орбиты возвращается «туда, откуда они начинались». (Другие эффекты также медленно изменяют форму и ориентацию орбиты Земли, и они, в сочетании с прецессией, создают различные циклы с разными периодами; см. Также Циклы Миланковича. Величина наклона Земли, в отличие от ее ориентации, также медленно меняется со временем, но этот эффект не связан напрямую с прецессией.)
По тем же причинам видимое положение Солнца относительно звездного фона в какое-то фиксированное время года медленно регрессирует на полные 360 ° через все двенадцать традиционных созвездий Солнца. зодиак, из расчета около 50,3 секунды дуги в год или 1 степень каждые 71,6 года.
В настоящее время скорость прецессии соответствует периоду в 25 772 года, но сама скорость несколько изменяется со временем (см. Значения ниже), поэтому нельзя сказать, что ровно через 25 772 года ось Земли вернется туда, где она находится сейчас.
Подробнее см. Смена полярных звезд и Полярный сдвиг и сдвиг равноденствий, ниже.
История
Эллинистический мир
Гиппарх
Открытие прецессии обычно приписывают Гиппарх (190–120 гг. До н.э.) Родос или же Никее, а Греческий астроном. В соответствии с Птолемей с Альмагест, Гиппарх измерил долготу Spica и другие яркие звезды. Сравнивая свои измерения с данными его предшественников, Тимохарис (320–260 гг. До н.э.) и Аристилль (~ 280 г. до н.э.), он пришел к выводу, что Спика сместился на 2 ° относительно осеннее равноденствие. Он также сравнил длину тропический год (время, необходимое Солнцу, чтобы вернуться в точку равноденствия) и звездный год (время, необходимое Солнцу, чтобы вернуться к неподвижной звезде), и обнаружил небольшое расхождение. Гиппарх пришел к выводу, что точки равноденствия движутся («прецессируют») по зодиаку и что скорость прецессии составляет не менее 1 ° за столетие, другими словами, полный цикл завершается не более чем за 36000 лет.[6]
Практически все сочинения Гиппарха потеряны, в том числе и его работа о прецессии. Они упоминаются Птолемеем, который объясняет прецессию как вращение небесная сфера вокруг неподвижной Земли. Разумно предположить, что Гиппарх, как и Птолемей, думал о прецессии в геоцентрический термины как движение небес, а не Земли.
Птолемей
Первый известный астроном, продолживший работу Гиппарха по прецессии, - это Птолемей во втором веке нашей эры. Птолемей измерил долготы Регулус, Spica, и другие яркие звезды с вариантом лунного метода Гиппарха, который не требовал затмений. Перед закатом он измерил продольную дугу, отделяющую Луну от Солнца. Затем, после захода солнца, он измерил дугу от Луны до звезды. Он использовал модель Гиппарха для вычисления долготы Солнца и внес поправки в движение Луны и ее параллакс (Evans 1998, стр. 251–255). Птолемей сравнил свои наблюдения с наблюдениями Гиппарха, Менелай Александрийский, Тимохарис, и Агриппа. Он обнаружил, что между временем Гиппарха и его собственным (около 265 лет) звезды переместились на 2 ° 40 ', или 1 ° за 100 лет (36 дюймов в год; принятая сегодня скорость составляет около 50 дюймов в год или 1 ° дюйма). 72 года). Однако возможно, что Птолемей просто доверял фигуре Гиппарха вместо того, чтобы делать свои собственные измерения. Он также подтвердил, что прецессия затронула все неподвижные звезды, а не только те, которые находятся около эклиптики, и что его цикл имел тот же период в 36000 лет, что и Гиппарх.[6]
Другие авторы
Большинство древних авторов не упоминали о прецессии и, возможно, не знали о ней. Например, Прокл отверг прецессию, а Теон Александрийский Комментатор Птолемея в четвертом веке принял объяснение Птолемея. Теон также сообщает об альтернативной теории:
- Согласно определенным мнениям древние астрологи полагают, что с определенной эпохи знаки солнцестояния имеют движение на 8 ° в порядке знаков, после чего они возвращаются на то же количество назад. . . . (Дрейер 1958, с. 204)
Вместо того, чтобы проходить через всю последовательность зодиака, точки равноденствия «трепетали» взад и вперед по дуге в 8 °. Теория трепет представлен Теоном как альтернатива прецессии.
Альтернативные теории открытий
Вавилоняне
Были сделаны различные утверждения о том, что другие культуры открыли прецессию независимо от Гиппарха. В соответствии с Аль-Баттани, то Халдейские астрономы отличил тропический и звездный год так что примерно к 330 г. до н.э. они были бы в состоянии описать прецессию, хотя и неточно, но такие утверждения обычно считаются необоснованными.[7]
майя
Археолог Сьюзан Милбрат предположил, что Мезоамериканский календарь длинного счета "30 000 лет с участием Плеяды... возможно, это была попытка вычислить прецессию равноденствия ".[8] Этого мнения придерживаются немногие другие профессионалы. ученые цивилизации майя.[нужна цитата ]
Древние египтяне
Были сделаны аналогичные заявления о том, что прецессия была известна в Древний Египет в династическую эпоху, до времен Гиппарха (Птолемеев период). Однако эти утверждения остаются спорными. Некоторые здания в Карнак Храмовые комплексы, например, якобы были ориентированы на точку на горизонте, где определенные звезды восходили или заходили в ключевые времена года.[нужна цитата ] Тем не менее, они вели точные календари, и если бы они записали дату реконструкции храма, было бы довольно просто построить приблизительную скорость прецессии. В Дендерский зодиак, звездную карту из Храм Хатхор в Дендера с позднего (птолемеевского) возраста якобы записывает прецессию равноденствий (Tompkins 1971). В любом случае, если древние египтяне знали о прецессии, их знания не записаны как таковые ни в одном из сохранившихся астрономических текстов.
Майкл Райс написал в своем Наследие Египта«Неизвестно, знали ли древние о механике Прецессии до ее определения Гиппархом Вифинием во втором веке до нашей эры, но как преданные наблюдатели за ночным небом они не могли не знать о ее последствиях». (стр. 128) Райс считает, что «Прецессия является фундаментальной для понимания того, что привело к развитию Египта» (стр. 10), в той мере, в какой «в некотором смысле Египет как национальное государство и царь Египта как живой бог - это продукт осознания египтянами астрономических изменений, вызванных огромным видимым движением небесных тел, которое подразумевает Прецессия ». (стр.56). Райс говорит, что «свидетельство того, что наиболее точные астрономические наблюдения практиковались в Египте в третьем тысячелетии до нашей эры (и, вероятно, даже до этой даты), ясно из точности, с которой пирамиды в Гизе выровнены по сторонам света, точность, которая могло быть достигнуто только путем их совмещения со звездами »(стр. 31). Египтяне также, как говорит Райс, должны были« изменить ориентацию храма, когда звезда, на которой он был первоначально установлен, переместился в свое положение как следствие Прецессии, что, кажется, происходило несколько раз во время Нового Царства ". (стр.170)
Индия
До 1200 г. в Индии существовало две теории трепет, одна со скоростью, а другая без скорости, а также несколько связанных моделей прецессии. В каждый из них были внесены незначительные изменения или исправления различных комментаторов. Доминирующей из этих трех была тревога, описанная в наиболее уважаемом индийском астрономическом трактате, Сурья Сиддханта (3: 9–12), состоит c. 400 но в течение следующих нескольких столетий пересматривались. Он использовал сидерическую эпоху, или аянамса, который до сих пор используется всеми Индийские календари, варьируясь в эклиптическая долгота от 19 ° 11 'до 23 ° 51', в зависимости от консультируемой группы.[9] В этой эпохе примерно 30 индийских календарных лет начинаются через 23–28 дней после современного весеннее равноденствие. Весеннее равноденствие Сурья Сиддханта либрированный на 27 ° в обоих направлениях от звездной эпохи. Таким образом, точка равноденствия сместилась на 54 ° в одном направлении, а затем на 54 ° назад в другом направлении. Этот цикл длился 7200 лет со скоростью 54 дюйма в год. Равноденствие совпало с эпохой начала Кали Юга в −3101 и снова через 3600 лет в 499. Направление изменилось с прямого на ретроградное на полпути между этими годами на −1301, когда оно достигло максимального отклонения в 27 °, и оставалось бы ретроградным, в том же направлении, что и современная прецессия, в течение 3600 г. лет до 2299 г.[10][11]:29–30
Другой трепет описал Варахамихира (c. 550). Его трепет состоял из дуги в 46 ° 40 ′ в одном направлении и возвращения в исходную точку. Половина этой дуги, 23 ° 20 ′, была отождествлена с максимумом Солнца. склонение по обе стороны от экватора во время солнцестояний. Но период не был указан, следовательно, годовая ставка не может быть установлена.[11]:27–28
Несколько авторов описали прецессию около 200000 революции в Кальпа из 4 320 000 000 лет, что составляет 200,000×360×3600/4,320,000,000 = 60 ″ / год. Вероятно, они отклонились даже от 200000 оборотов, чтобы сделать накопленную прецессию нулевой около 500. Visnucandra (c. 550–600) упоминает 189,411 оборотов в кальпе или 56,8 ″ / год. Бхаскара I (c. 600–680) упоминаний [1] 94 110 оборотов в кальпе или 58,2 ″ / год. Бхаскара II (c. 1150) упоминает 199,699 оборотов в кальпе или 59,9 ″ / год.[11]:32–33
Китайская астрономия
Юй Си (четвертый век нашей эры) был первым Китайский астроном чтобы упомянуть прецессию. Он оценил скорость прецессии в 1 ° за 50 лет (Pannekoek 1961: 92).
Средние века и ренессанс
В средневековая исламская астрономия, прецессия была известна на основе Альмагеста Птолемея и наблюдений, уточняющих это значение.
Аль-Баттани, в его Зидж аль-Саби после упоминания Гиппарха, вычисляющего прецессию, и значения Птолемея, равного 1 градусу на 100 солнечных лет, говорит, что он измерил прецессию и обнаружил, что она составляет один градус на 66 солнечных лет.[12]
Впоследствии Ас-Суфи упоминает те же ценности в своих Книга неподвижных звезд, что значение прецессии Птолемея составляет 1 градус на 100 солнечных лет. Затем он цитирует другое значение из Зидж Аль Мумтахан, что было сделано во время Аль-Мамун 1 градус за каждые 66 солнечных лет. Он также цитирует вышеупомянутые Аль-Баттани с Зидж аль-Саби как корректировка координат звезд на 11 градусов и 10 угловых минут, чтобы учесть разницу между временем Аль-Баттани и временем Птолемея.[13]
Позже Зидж-и Ильхани составлено в Обсерватория Мараге устанавливает прецессию равноденствий на уровне 51 угловой секунды в год, что очень близко к современному значению в 50,2 угловой секунды.[14]
В средние века исламские и латинские христианские астрономы рассматривали «трепет» как движение неподвижных звезд. Добавлено в прецессия. Эту теорию обычно приписывают Араб астроном Сабит ибн Курра, но атрибуция была оспорена в наше время. Николай Коперник опубликовал другой отчет о трепете в De Revolutionibus orbium coelestium (1543). В этой работе впервые упоминается прецессия как результат движения земной оси. Коперник охарактеризовал прецессию как третье движение Земли.[15]
Современный период
Более века спустя прецессия была объяснена в Исаак Ньютон с Philosophiae Naturalis Principia Mathematica (1687), как следствие гравитация (Эванс 1998, стр. 246). Однако первоначальные уравнения прецессии Ньютона не работали и были значительно пересмотрены Жан ле Ронд д'Аламбер и последующие ученые.
Открытие Гиппарха
Гиппарх рассказал о своем открытии в О смещении точек Солнца и Равноденствия (описано в Альмагест III.1 и VII.2). Он измерил эклиптику долгота звезды Spica во время лунных затмений и обнаружил, что он находился примерно в 6 ° к западу от осеннее равноденствие. Сравнивая свои измерения с измерениями Тимохарис Александрии (современник Евклид, который работал с Аристилль в начале 3-го века до нашей эры) он обнаружил, что долгота Спики за это время уменьшилась примерно на 2 ° (точные годы не упоминаются в Альмагесте). Также в VII.2 Птолемей дает более точные наблюдения двух звезд, включая Спику, и заключает, что в каждом случае изменение 2 °: 40 'произошло в течение 128 г. до н.э. и 139 г. н.э. (следовательно, 1 ° за столетие или один полный цикл за 36000 г.). лет, то есть прецессионный период Гиппарха, о котором сообщает Птолемей; см. страницу 328 в переводе Тумера Альмагеста, издание 1998 г.)). Он также заметил это движение у других звезд. Он предположил, что со временем смещались только звезды возле зодиака. Птолемей назвал это своей «первой гипотезой» (Альмагест VII.1), но не сообщил о какой-либо более поздней гипотезе, которую мог бы придумать Гиппарх. Гиппарх, по-видимому, ограничил свои предположения, потому что у него было всего несколько старых наблюдений, которые не были очень надежными.
Зачем Гиппарху понадобился лунное затмение измерить положение звезды? Точки равноденствия не отмечены на небе, поэтому ему нужна была Луна в качестве ориентира. Гиппарх уже разработал способ вычисления долготы Солнца в любой момент. Лунное затмение происходит во время Полнолуние, когда Луна в оппозиция. В середине затмения Луна находится точно на 180 ° от Солнца. Считается, что Гиппарх измерил продольную дугу, отделяющую Спику от Луны. К этому значению он добавил рассчитанную долготу Солнца плюс 180 ° долготы Луны. Он проделал ту же процедуру с данными Тимохариса (Evans 1998, p. 251). Между прочим, наблюдения, подобные этим затмениям, являются основным источником данных о том, когда работал Гиппарх, поскольку другая биографическая информация о нем минимальна. Лунные затмения, которые он наблюдал, например, имели место 21 апреля 146 г. до н. Э. И 21 марта 135 г. до н. Э. (Toomer 1984, p. 135, n. 14).
Гиппарх также изучал прецессию в О продолжительности года. Для понимания его работы важны два типа года. В тропический год это время, в течение которого солнце, если смотреть с Земли, возвращается в то же положение по эклиптике (его путь среди звезд на небесной сфере). В звездный год - это промежуток времени, который требуется Солнцу, чтобы вернуться в то же положение по отношению к звездам небесной сферы. Прецессия заставляет звезды немного менять свою долготу каждый год, поэтому звездный год длиннее тропического. Используя наблюдения равноденствий и солнцестояний, Гиппарх обнаружил, что длина тропического года составляла 365 + 1 / 4-1 / 300 дней, или 365,24667 дней (Evans 1998, p. 209). Сравнивая это с продолжительностью сидерического года, он подсчитал, что скорость прецессии составляет не менее 1 ° за столетие. Исходя из этой информации, можно вычислить, что его значение для звездного года составляло 365 + 1/4 + 1/144 дня (Toomer 1978, стр. 218). Давая минимальную ставку, он, возможно, допускал ошибки в наблюдении.
Чтобы приблизиться к своему тропическому году, Гиппарх создал свой собственный лунно-солнечный календарь путем изменения тех из Метон и Каллипп в В интеркалярные месяцы и дни (теперь потеряно), как описано Птолемей в Альмагест III.1 (Toomer 1984, стр. 139). В Вавилонский календарь использовался цикл из 235 лунных месяцев за 19 лет, начиная с 499 г. до н.э. (с тремя исключениями до 380 г. до н.э.), но не использовалось указанное количество дней. В Метонический цикл (432 г. до н.э.) этим 19 годам было отнесено 6940 дней, что дало средний год 365 + 1/4 + 1/76 или 365,26316 дней. В Каллиппический цикл (330 г. до н.э.) упал на один день с четырех циклов Метона (76 лет) на средний год 365 + 1/4 или 365,25 дня. Гиппарх исключил еще один день из четырех каллиптических циклов (304 года), создав Гиппархический цикл со средним годом 365 + 1 / 4-1 / 304 или 365,24671 дня, что было близко к его тропическому году 365 + 1 / 4-1 / 300 или 365,24667 дней.
Мы находим математические подписи Гиппарха в Антикитерский механизм, древний астрономический компьютер второго века до нашей эры. Механизм основан на солнечном году, Метонический цикл, который представляет собой период, когда Луна снова появляется в том же месте на небе с той же фазой (полная Луна появляется в том же месте на небе примерно через 19 лет), Каллипический цикл (что составляет четыре цикла Метона и более точно), Цикл Сароса и Циклы экзелигмоса (три цикла Сароса для точного предсказания затмения). Изучение антикиферского механизма доказывает, что древние использовали очень точные календари, основанные на всех аспектах движения Солнца и Луны в небе. Фактически, лунный механизм, который является частью антикиферского механизма, изображает движение Луны и ее фазу в течение заданного времени, используя цепочку из четырех шестерен с устройством штифта и паза, которое дает переменную скорость Луны, которая очень близка ко второму закону Кеплер, т.е. учитывает быстрое движение Луны на перигей и более медленное движение на апогей. Это открытие доказывает, что математика Гиппарха была намного более продвинутой, чем описывает Птолемей в своих книгах, поскольку очевидно, что он разработал хорошее приближение Второй закон Кеплера.
Митраические созвездия
В Митраические мистерии, в просторечии также известный как Митраизм, был неоплатоническим таинственный культ римского бога Митры. Практически полное отсутствие письменных описаний или Священных Писаний требует реконструкции верований и практик на основе археологических свидетельств, например, найденных в митраистских храмах (в наше время называемых Митрея ), которые были реальными или искусственными «пещерами», представляющими космос. До 1970-х годов большинство ученых следовали Франц Кюмон в идентификации Митры как продолжения персидского бога Митра. Гипотеза Кюмона о непрерывности и сопутствующая ему теория о том, что астрологический компонент был поздним и неважным нарастанием, больше не соблюдается. Сегодня культ и его верования признаны продуктом (греко) римской мысли, с астрологическим компонентом, даже более выраженным, чем и без того очень ориентированные на астрологию римские верования в целом. Детали, однако, обсуждаются.[16]
Что касается осевой прецессии, один исследователь митраизма Дэвид Уланси,[16] интерпретировал Митру как олицетворение силы, ответственной за прецессию. Он утверждает, что культ был религиозным ответом на открытие Гиппархом прецессии, которое - с древней геоцентрической точки зрения - равносильно открытию того, что весь космос (т.е. самый внешний небесная сфера неподвижных звезд) двигался неизвестным ранее образом. Его анализ основан на так называемом "тавроктония ": изображение Митры, убивающего быка, которое находилось в центре каждого митраистского храма. В стандартной тавроктонии Митра и бык сопровождаются собака, а змея, а ворон, а скорпион. По Улансею, тавроктония - это карта звездного неба. Бык Телец, созвездие зодиака. в астрологический возраст до времени Гиппарха, весеннее равноденствие произошло, когда Солнце находилось в созвездии Тельца, а в ту предыдущую эпоху созвездия Canis Minor (Собака), Гидра (Змея), Корвус (Ворон), и Скорпион (Скорпион) - то есть созвездия, соответствующие животным, изображенным в тавроктонии, - все лежали на небесном экваторе (положение которого смещено из-за прецессии) и, таким образом, занимали привилегированное положение на небе в ту эпоху. Сам Митра представляет созвездие Персей, который расположен прямо над Тельцом-Быком: то же место занимает Митра на изображении тавроктонии. Убийство Митрой Быка, согласно этому рассуждению, представляло собой силу, которой обладает этот новый бог, чтобы сдвинуть всю космическую структуру, повернув космическую сферу так, чтобы место весеннего равноденствия покинуло созвездие Тельца (переход, символизируемый убийством Быка), а Собака, Змея, Ворон и Скорпион также потеряли свое привилегированное положение на небесном экваторе.[16]
В иконография также содержит два двойника с факелами (Cautes и Cautopates ) обрамляют изображение убийцы быка - один держит факел, направленный вверх, а другой - факел, направленный вниз. Этих факелоносцев иногда изображают, когда один из них (горящий факел) держит или ассоциируется с Быком и деревом с листьями, а другой (факел опущен) держит или связан со Скорпионом и деревом с фруктами. Уланси интерпретирует этих факелоносцев как представление весеннего равноденствия (факел вверх, дерево с листьями, Бык) и осеннего равноденствия (факел вниз, дерево с фруктами, Скорпион) в Тельце и Скорпионе соответственно, где были точки равноденствия во время предшествующий «Век Тельца» символизировал тавроктонию в целом. Таким образом, Уланси заключает, что митраистская иконография была «астрономическим кодом», секрет которого заключался в существовании нового космического божества, неизвестного тем, кто вне культа, чьим фундаментальным атрибутом была его способность изменять структуру всего космоса и тем самым управлять астрологией. силы, которые считали в то время определяющими человеческое существование, давая ему силу даровать своим приверженцам успех в жизни и спасение после смерти (то есть безопасное путешествие по планетным сферам и последующее бессмертное существование в царстве звезд).[16]
Смена полярных звезд

Следствием прецессии является изменение Полярная звезда. В настоящее время Полярная звезда очень хорошо подходит для обозначения положения северного полюса мира, поскольку Полярная звезда - умеренно яркая звезда с визуальным величина 2,1 (переменная), и он расположен примерно в одном градусе от полюса, и нет звезд подобной яркости слишком близко.[17]
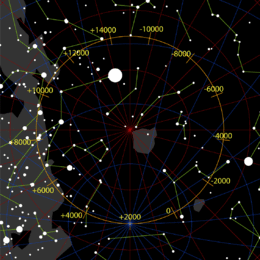
Предыдущая полярная звезда была Кочаб (Beta Ursae Minoris, β UMi, β Ursae Minoris), ярчайшая звезда в чаше «Малой Медведицы», расположенная в 16 градусах от Полярной звезды. Он выполнял эту роль с 1500 г. до н.э. до 500 г. н.э.[18] В свое время он не был таким точным, как сегодня Полярная звезда.[18] Сегодня Кочаб и его сосед Феркад называют «Стражами полюса» (то есть Полярной звезды).[18]
С другой стороны, Тубан в созвездие Драко, который был полярной звездой в 3000 г. до н.э., гораздо менее заметен при величине 3,67 (одна пятая яркости Полярной звезды); сегодня это невидимо в светозагрязненный городское небо.
Когда Полярная звезда снова станет северной звездой около 27 800, тогда она будет дальше от полюса, чем сейчас, из-за ее правильное движение, а в 23600 г. до н.э. он подошел ближе к полюсу.
В данный момент найти южный небесный полюс на небе труднее, так как эта область является особенно мягкой частью неба, а номинальная звезда южного полюса - Сигма Октантис, которая с величиной 5,5 едва заметна невооруженным глазом даже в идеальных условиях. Однако это изменится с 80-го по 90-е века, когда южный небесный полюс пройдет через Ложный крест.
Эта ситуация также видна на звездной карте. Ориентация южного полюса смещается к Южный Крест созвездие. Последние 2000 лет или около того Южный Крест указывал на южный полюс мира. Как следствие, созвездие трудно увидеть из субтропических северных широт, в отличие от того, как оно было во времена древние греки. Южный Крест можно увидеть даже с севера, до Майами (около 25 ° северной широты), но только зимой / ранней весной.
Полярный сдвиг и сдвиг равноденствий


Изображения справа пытаются объяснить связь между прецессией оси Земли и смещением точек равноденствия. Эти изображения показывают положение оси Земли на небесная сфера, фиктивная сфера, на которой звезды размещаются в соответствии с их положением, если смотреть с Земли, независимо от их фактического расстояния. Первое изображение показывает небесную сферу снаружи с созвездиями в зеркальном отображении. Второе изображение показывает перспективу околоземной позиции, видимой через очень широкоугольный объектив (из-за которого возникает кажущееся искажение).
Ось вращения Земли описывает за период в 25700 лет небольшой круг (синий) среди звезд с центром в эклиптика северный полюс (синий E) и с угловым радиусом около 23,4 °, углом, известным как наклон эклиптики. Направление прецессии противоположно суточному вращению Земли вокруг своей оси. Оранжевая ось была осью вращения Земли 5000 лет назад, когда она указывала на звезду Тубан. Желтая ось, указывающая на Полярную звезду, теперь отмечает ось.
The equinoxes occur where the celestial equator intersects the ecliptic (red line), that is, where the Earth's axis is perpendicular to the line connecting the centers of the Sun and Earth. (Note that the term "equinox" here refers to a point on the celestial sphere so defined, rather than the moment in time when the Sun is overhead at the Equator, though the two meanings are related.) When the axis precesses from one orientation to another, the equatorial plane of the Earth (indicated by the circular grid around the equator) moves. The celestial equator is just the Earth's equator projected onto the celestial sphere, so it moves as the Earth's equatorial plane moves, and the intersection with the ecliptic moves with it. The positions of the poles and equator on Earth do not change, only the orientation of the Earth against the fixed stars.
As seen from the orange grid, 5,000 years ago, the vernal equinox was close to the star Aldebaran из Телец. Now, as seen from the yellow grid, it has shifted (indicated by the red arrow) to somewhere in the constellation of Pisces.
Still pictures like these are only first approximations, as they do not take into account the variable speed of the precession, the variable obliquity of the ecliptic, the planetary precession (which is a slow rotation of the ecliptic plane itself, presently around an axis located on the plane, with longitude 174°.8764) and the proper motions of the stars.

The precessional eras of each constellation, often known as Great Months, are approximately:[19]
| Constellation | Year entering | Year exiting |
|---|---|---|
| Телец | 4500 BC | 2000 BC |
| Овен | 2000 BC | 100 BC |
| Pisces | 100 BC | AD 2700 |
Причина
The precession of the equinoxes is caused by the gravitational forces of the солнце и Луна, and to a lesser extent other bodies, on the Earth. It was first explained by Sir Isaac Newton.[20]
Axial precession is similar to the precession of a spinning top. In both cases, the applied force is due to gravity. For a spinning top, this force tends to be almost parallel to the rotation axis initially and increases as the top slows down. For a gyroscope on a stand it can approach 90 degrees. For the Earth, however, the applied forces of the Sun and the Moon are closer to perpendicular to the axis of rotation.
The Earth is not a perfect sphere but an oblate spheroid, with an equatorial diameter about 43 kilometers larger than its polar diameter. Because of the Earth's axial tilt, during most of the year the half of this bulge that is closest to the Sun is off-center, either to the north or to the south, and the far half is off-center on the opposite side. The gravitational pull on the closer half is stronger, since gravity decreases with the square of distance, so this creates a small torque on the Earth as the Sun pulls harder on one side of the Earth than the other. The axis of this torque is roughly perpendicular to the axis of the Earth's rotation so the axis of rotation precesses. If the Earth were a perfect sphere, there would be no precession.
This average torque is perpendicular to the direction in which the rotation axis is tilted away from the ecliptic pole, so that it does not change the axial tilt itself. The magnitude of the torque from the Sun (or the Moon) varies with the angle between the Earth's spin axis direction and that of the gravitational attraction. It approaches zero when they are perpendicular. For example, this happens at the equinoxes in the case of the interaction with the Sun. This can be seen to be since the near and far points are aligned with the gravitational attraction, so there is no torque due to the difference in gravitational attraction.
Although the above explanation involved the Sun, the same explanation holds true for any object moving around the Earth, along or close to the ecliptic, notably, the Moon. The combined action of the Sun and the Moon is called the lunisolar precession. In addition to the steady progressive motion (resulting in a full circle in about 25,700 years) the Sun and Moon also cause small periodic variations, due to their changing positions. These oscillations, in both precessional speed and axial tilt, are known as the nutation. The most important term has a period of 18.6 years and an amplitude of 9.2 arcseconds.[21]
In addition to lunisolar precession, the actions of the other planets of the Solar System cause the whole ecliptic to rotate slowly around an axis which has an ecliptic longitude of about 174° measured on the instantaneous ecliptic. This so-called planetary precession shift amounts to a rotation of the ecliptic plane of 0.47 seconds of arc per year (more than a hundred times smaller than lunisolar precession). The sum of the two precessions is known as the general precession.
Equations

В tidal force on Earth due to a perturbing body (Sun, Moon or planet) is expressed by Newton's law of universal gravitation, whereby the gravitational force of the perturbing body on the side of Earth nearest is said to be greater than the gravitational force on the far side by an amount proportional to the difference in the cubes of the distances between the near and far sides. If the gravitational force of the perturbing body acting on the mass of the Earth as a point mass at the center of Earth (which provides the centripetal force causing the orbital motion) is subtracted from the gravitational force of the perturbing body everywhere on the surface of Earth, what remains may be regarded as the tidal force. This gives the paradoxical notion of a force acting away from the satellite but in reality it is simply a lesser force toward that body due to the gradient in the gravitational field. For precession, this tidal force can be grouped into two forces which only act on the equatorial bulge outside of a mean spherical radius. Этот couple can be decomposed into two pairs of components, one pair parallel to Earth's equatorial plane toward and away from the perturbing body which cancel each other out, and another pair parallel to Earth's rotational axis, both toward the эклиптика plane.[22] The latter pair of forces creates the following крутящий момент вектор on Earth's equatorial bulge:[4]
куда
- GM = standard gravitational parameter of the perturbing body
- р = geocentric distance to the perturbing body
- C = moment of inertia around Earth's axis of rotation
- А = moment of inertia around any equatorial diameter of Earth
- C − А = moment of inertia of Earth's equatorial bulge (C > А)
- δ = declination of the perturbing body (north or south of equator)
- α = right ascension of the perturbing body (east from vernal равноденствие ).
The three unit vectors of the torque at the center of the Earth (top to bottom) are Икс on a line within the ecliptic plane (the intersection of Earth's equatorial plane with the ecliptic plane) directed toward the vernal equinox, у on a line in the ecliptic plane directed toward the summer solstice (90° east of Икс), и z on a line directed toward the north pole of the ecliptic.
The value of the three sinusoidal terms in the direction of Икс (грехδ потому чтоδ грехα) for the Sun is a sine squared waveform varying from zero at the equinoxes (0°, 180°) to 0.36495 at the solstices (90°, 270°). The value in the direction of у (грехδ потому чтоδ (−cosα)) for the Sun is a sine wave varying from zero at the four equinoxes and solstices to ±0.19364 (slightly more than half of the sine squared peak) halfway between each equinox and solstice with peaks slightly skewed toward the equinoxes (43.37°(−), 136.63°(+), 223.37°(−), 316.63°(+)). Both solar waveforms have about the same peak-to-peak amplitude and the same period, half of a revolution or half of a year. The value in the direction of z is zero.
The average torque of the sine wave in the direction of у is zero for the Sun or Moon, so this component of the torque does not affect precession. The average torque of the sine squared waveform in the direction of Икс for the Sun or Moon is:
куда
- = semimajor axis of Earth's (Sun's) orbit or Moon's orbit
- е = eccentricity of Earth's (Sun's) orbit or Moon's orbit
and 1/2 accounts for the average of the sine squared waveform, accounts for the average distance cubed of the Sun or Moon from Earth over the entire elliptical orbit,[23] и (the angle between the equatorial plane and the ecliptic plane) is the maximum value of δ for the Sun and the average maximum value for the Moon over an entire 18.6 year cycle.
Precession is:
куда ω is Earth's angular velocity и Cω is Earth's angular momentum. Thus the first order component of precession due to the Sun is:[4]
whereas that due to the Moon is:
куда я is the angle between the plane of the Moon's orbit and the ecliptic plane. In these two equations, the Sun's parameters are within square brackets labeled S, the Moon's parameters are within square brackets labeled L, and the Earth's parameters are within square brackets labeled E. The term accounts for the inclination of the Moon's orbit relative to the ecliptic. Период, термин (C−A)/C is Earth's dynamical ellipticity or flattening, which is adjusted to the observed precession because Earth's internal structure is not known with sufficient detail. If Earth were однородный the term would equal its third eccentricity squared,[24]
where a is the equatorial radius (6378137 m) and c is the polar radius (6356752 m), so е2 = 0.003358481.
Applicable parameters for J2000.0 rounded to seven significant digits (excluding leading 1) are:[25][26]
| солнце | Луна | земной шар |
|---|---|---|
| GM = 1.3271244×1020 м3/s2 | GM = 4.902799×1012 м3/s2 | (C − А)/C = 0.003273763 |
| а = 1.4959802×1011 м | а = 3.833978×108 м | ω = 7.292115×10−5 rad/s |
| е = 0.016708634 | е = 0.05554553 | = 23.43928° |
| я= 5.156690° |
which yield
- dψS/dt = 2.450183×10−12 /s
- dψL/dt = 5.334529×10−12 /s
both of which must be converted to "/a (arcseconds/annum) by the number of угловые секунды in 2π радианы (1.296×106"/2π) and the number of seconds in one annum (а Julian year ) (3.15576×107s/a):
- dψS/dt = 15.948788"/a vs 15.948870"/a from Williams[4]
- dψL/dt = 34.723638"/a vs 34.457698"/a from Williams.
The solar equation is a good representation of precession due to the Sun because Earth's orbit is close to an ellipse, being only slightly perturbed by the other planets. The lunar equation is not as good a representation of precession due to the Moon because the Moon's orbit is greatly distorted by the Sun and neither the radius nor the eccentricity is constant over the year.
Values
Саймон Ньюкомб 's calculation at the end of the 19th century for general precession (п) in longitude gave a value of 5,025.64 arcseconds per tropical century, and was the generally accepted value until artificial satellites delivered more accurate observations and electronic computers allowed more elaborate models to be calculated. Jay Henry Lieske developed an updated theory in 1976, where п equals 5,029.0966 arcseconds (or 1.3969713 degrees) per Julian century. Modern techniques such as VLBI и LLR allowed further refinements, and the Международный астрономический союз adopted a new constant value in 2000, and new computation methods and polynomial expressions in 2003 and 2006; то accumulated precession is:[27]
- пА = 5,028.796195×Т + 1.1054348×Т2 + higher order terms,
in arcseconds, with Т, the time in Julian centuries (that is, 36,525 days) since the epoch of 2000.
В rate of precession is the derivative of that:
- п = 5,028.796195 + 2.2108696×Т + higher order terms.
The constant term of this speed (5,028.796195 arcseconds per century in above equation) corresponds to one full precession circle in 25,771.57534 years (one full circle of 360 degrees divided with 5,028.796195 arcseconds per century)[27] although some other sources put the value at 25771.4 years, leaving a small uncertainty.
The precession rate is not a constant, but is (at the moment) slowly increasing over time, as indicated by the linear (and higher order) terms in Т. In any case it must be stressed that this formula is only valid over a limited time period. It is a polynomial expression centred on the J2000 datum, empirically fitted to observational data, not on a deterministic model of the solar system. It is clear that if Т gets large enough (far in the future or far in the past), the Т² term will dominate and п will go to very large values. In reality, more elaborate calculations on the numerical model of the Solar System show that the precessional constants have a period of about 41,000 years, the same as the obliquity of the ecliptic. Note that the constants mentioned here are the linear and all higher terms of the formula above, not the precession itself. То есть,
- п = А + BT + CT2 + …
is an approximation of
- п = а + б sin (2πТ/п), куда п is the 41,000-year period.
Theoretical models may calculate the constants (coefficients) corresponding to the higher powers of Т, but since it is impossible for a (finite) polynomial to match a periodic function over all numbers, the difference in all such approximations will grow without bound as Т increases. However, greater accuracy can be obtained over a limited time span by fitting a high enough order polynomial to observation data, rather than a necessarily imperfect dynamic numerical model. So for present flight trajectory calculations of artificial satellites and spacecraft, the polynomial method gives better accuracy. In that respect, the International Astronomical Union chose the best-developed available theory. For up to a few centuries in the past and the future, all formulas do not diverge very much. For up to a few thousand years in the past and the future, most agree to some accuracy. For eras farther out, discrepancies become too large – the exact rate and period of precession may not be computed using these polynomials even for a single whole precession period.
The precession of Earth's axis is a very slow effect, but at the level of accuracy at which astronomers work, it does need to be taken into account on a daily basis. Note that although the precession and the tilt of Earth's axis (the obliquity of the ecliptic) are calculated from the same theory and thus, are related to each other, the two movements act independently of each other, moving in opposite directions.
Precession exhibits a secular decrease due to tidal dissipation from 59"/a to 45"/a (a = annum = Julian year ) during the 500 million year period centered on the present. After short-term fluctuations (tens of thousands of years) are averaged out, the long-term trend can be approximated by the following polynomials for negative and positive time from the present in "/a, where Т в billions of Julian years (Ga):[28]
- п− = 50.475838 − 26.368583Т + 21.890862Т2
- п+ = 50.475838 − 27.000654Т + 15.603265Т2
Precession will be greater than п+ by the small amount of +0.135052"/a between +30 Ma и +130 Ma. The jump to this excess over п+ will occur in only 20 Ma beginning now because the secular decrease in precession is beginning to cross a resonance in Earth's orbit caused by the other planets.
According to Ward, when, in about 1,500 million years, the distance of the Moon, which is continuously increasing from tidal effects, has increased from the current 60.3 to approximately 66.5 Earth radii, resonances from planetary effects will push precession to 49,000 years at first, and then, when the Moon reaches 68 Earth radii in about 2,000 million years, to 69,000 years. This will be associated with wild swings in the obliquity of the ecliptic as well. Ward, however, used the abnormally large modern value for tidal dissipation. Using the 620-million year average provided by tidal rhythmites of about half the modern value, these resonances will not be reached until about 3,000 and 4,000 million years, respectively. However, due to the gradually increasing luminosity of the Sun, the oceans of the Earth will have vaporized before that time (about 2,100 million years from now).
Смотрите также
- Age of Aquarius
- Astrological age
- Astronomical nutation
- Axial tilt
- Euler angles
- Longitude of vernal equinox
- Milankovitch cycles
- Sidereal year
Рекомендации
- ^ а б Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) Explanatory Supplement to the Astronomical Almanac. Sausalito: University Science Books. п. 99.
- ^ а б c Astro 101 – Precession of the Equinox В архиве 2009-01-02 at the Wayback Machine, Western Washington University Планетарий, accessed 30 December 2008
- ^ Robert Main, Practical and Spherical Astronomy (Cambridge: 1863) pp.203–4.
- ^ а б c d Williams, James G. (1994). "Contribution to the Earth's Obliquity Rate, Precession, and Nutation". Астрономический журнал. 108: 711. Bibcode:1994AJ....108..711W. Дои:10.1086/117108.
- ^ "IAU 2006 Resolution B1: Adoption of the P03 Precession Theory and Definition of the Ecliptic" (PDF). Архивировано из оригинал (PDF) on 21 October 2011. Получено 28 февраля 2009.
- ^ а б Птолемей (1998) [1984 c. 150], Ptolemy's Almagest, translated by Toomer, G. J., Princeton University Press, pp. 131–141, 321–340, ISBN 0-691-00260-6
- ^ Neugebauer, O. (1950). "The Alleged Babylonian Discovery of the Precession of the Equinoxes". Journal of the American Oriental Society. 70 (1): 1–8. Дои:10.2307/595428. JSTOR 595428.
- ^ Susan Milbrath, "Just How Precise is Maya Astronomy?", Institute of Maya Studies newsletter, December 2007.
- ^ Government of India (1955), Report of the Calendar Reform Committee (PDF), Council of Scientific and Industrial Research, p. 262,
The longitudes of the first point of Aries, according to the two schools therefore differ by 23°[51]′ (–) 19°11′ ... [Upper limit was increased by 42′ of accumulated precession 1950–2000.]
- ^ Сурья (1935) [1860], Gangooly, Phanindralal (ed.), Translation of Surya Siddhanta: A Textbook of Hindu Astronomy, translated by Burgess, Ebenezzer, University of Calcutta, p. 114
- ^ а б c Pingree, David (1972), "Precession and trepidation in Indian astronomy before A.D. 1200", Journal for the History of Astronomy, 3: 27–35, Bibcode:1972JHA.....3...27P, Дои:10.1177/002182867200300104
- ^ Al-Battani. "Zij Al-Sabi'". Архивировано из оригинал on 5 January 2017. Получено 30 сентября 2017.
- ^ Al-Sufi. "Book of Fixed Stars".
- ^ Rufus, W. C. (May 1939). "The Influence of Islamic Astronomy in Europe and the Far East". Популярная астрономия. 47 (5): 233–238 [236]. Bibcode:1939PA.....47..233R..
- ^ Gillispie, Charles Coulston (1960). The Edge of Objectivity: An Essay in the History of Scientific Ideas. Издательство Принстонского университета. п. 24. ISBN 0-691-02350-6.
- ^ а б c d Ulansey, David (1991), Mithraism: The Cosmic Mysteries of Mithras, mysterium.com
- ^ van Leeuwen, F. (2007). "HIP 11767". Hipparcos, the New Reduction. Получено 1 марта 2011.
- ^ а б c Benningfield, Damond (14 June 2015). "Kochab". Stardate Magazine. University of Texas McDonald Observatory. Получено 14 июн 2015.
- ^ Kaler, James B. (2002). The ever-changing sky: a guide to the celestial sphere (Reprint). Издательство Кембриджского университета. п. 152. ISBN 978-0521499187.
- ^ The Columbia Electronic Encyclopedia, 6th ed., 2007
- ^ "Basics of Space Flight, Chapter 2". Лаборатория реактивного движения. Jet Propulsion Laboratory/NASA. 29 октября 2013 г.. Получено 26 марта 2015.
- ^ Ivan I. Mueller, Spherical and practical astronomy as applied to geodesy (New York: Frederick Unger, 1969) 59.
- ^ G. Boué & J. Laskar, "Precession of a planet with a satellite", Икар 185 (2006) 312–330, p.329.
- ^ George Biddel Airy, Mathematical tracts on the lunar and planetary theories, the figure of the earth, precession and nutation, the calculus of variations, and the undulatory theory of optics (third edititon, 1842) 200.
- ^ Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.; Laskar, J. (1994). "Numerical expressions for precession formulae and mean elements for the Moon and the planets". Astronomy and Astrophysics. 282: 663. Bibcode:1994A&A...282..663S.
- ^ Dennis D. McCarthy, IERS Technical Note 13 – IERS Standards (1992) (Postscript, use PS2PDF ).
- ^ а б N. Capitaine и другие. 2003, п. 581 expression 39
- ^ Laskar, J.; Robutel, P.; Joutel, F.; Gastineau, M.; Correia, A. C. M.; Levrard, B. (2004). "A long-term numerical solution for the insolation quantities of the Earth". Астрономия и астрофизика. 428: 261–285. Дои:10.1051/0004-6361:20041335.
Библиография
- Berger, A. L. (1976). "Obliquity and precession for the last 5000000 years". Astronomy and Astrophysics. 51 (1): 127–135. Bibcode:1976A&A....51..127B.
- Capitaine, N. (2003). "Expressions for IAU 2000 precession quantities". Астрономия и астрофизика. 412 (2): 567–586. Bibcode:2003A&A...412..567C. Дои:10.1051/0004-6361:20031539.
- Dreyer, J. L. E.. A History of Astronomy from Thales to Kepler. 2-е изд. New York: Dover, 1953.
- Evans, James. The History and Practice of Ancient Astronomy. New York: Oxford University Press, 1998.
- Explanatory supplement to the Astronomical ephemeris and the American ephemeris and nautical almanac
- Hilton, J.L. (2006). "Report of the International Astronomical Union Division I Working Group on Precession and the Ecliptic" (PDF). Celestial Mechanics and Dynamical Astronomy. 94 (3): 351–367. Bibcode:2006CeMDA..94..351H. Дои:10.1007/s10569-006-0001-2.
- Lieske, J. H.; Lederle, T.; Fricke, W. (1977). "Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants". Astron. Astrophys. 58: 1–16. Bibcode:1977A&A....58....1L.
- Precession and the Obliquity of the Ecliptic has a comparison of values predicted by different theories
- Pannekoek, A. A History of Astronomy. New York: Dover, 1961.
- Parker, Richard A. "Egyptian Astronomy, Astrology, and Calendrical Reckoning." Dictionary of Scientific Biography 15:706–727.
- Rice, Michael (1997), Egypt's Legacy: The archetypes of Western civilization, 3000–30 BC, London and New York.
- Schütz, Michael (2000). "Hipparch und die Entdeckung der Präzession. Bemerkungen zu David Ulansey, Die Ursprünge des Mithraskultes". Electronic Journal of Mithraic Studies (на немецком). 1. Архивировано из оригинал on 4 November 2013.
- Simon, J. L. (1994). "Numerical expressions for precession formulae and mean elements for the Moon and the planets". Astronomy and Astrophysics. 282: 663–683. Bibcode:1994A&A...282..663S.
- Tomkins, Peter. Secrets of the Great Pyramid. With an appendix by Livio Catullo Stecchini. New York: Harper Colophon Books, 1971.
- Toomer, G. J. "Hipparchus." Dictionary of Scientific Biography. Vol. 15:207–224. New York: Charles Scribner's Sons, 1978.
- Toomer, G. J. Ptolemy's Almagest. London: Duckworth, 1984.
- Ulansey, David. The Origins of the Mithraic Mysteries: Cosmology and Salvation in the Ancient World. New York: Oxford University Press, 1989.
- Vondrak, J.; Capitaine, N.; Wallace, P. (2011). "New precession expressions, valid for long time intervals". Астрономия и астрофизика. 534: A22. Bibcode:2011A&A...534A..22V. Дои:10.1051/0004-6361/201117274.
- Ward, W. R. (1982). "Comments on the long-term stability of the earth's obliquity". Икар. 50 (2–3): 444–448. Bibcode:1982Icar...50..444W. Дои:10.1016/0019-1035(82)90134-8.
внешняя ссылка
- D'Alembert and Euler's Debate on the Solution of the Precession of the Equinoxes
- Bowley, Roger; Merrifield, Michael. "Axial Precession". Sixty Symbols. Brady Haran для Ноттингемский университет.
- Forced precession and nutation of Earth







![{ displaystyle { frac {d psi _ {S}} {dt}} = { frac {3} {2}} left [{ frac {GM} {a ^ {3} (1-e ^ {2}) ^ {3/2}}} right] _ {S} left [{ frac {(CA)} {C}} { frac { cos epsilon} { omega}} right ] _ {E}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a0dcfbeb69856a5bb6657210618dbb02396585b)
![{ displaystyle { frac {d psi _ {L}} {dt}} = { frac {3} {2}} left [{ frac {GM (1-1,5 sin ^ {2} i) } {a ^ {3} (1-e ^ {2}) ^ {3/2}}} right] _ {L} left [{ frac {(CA)} {C}} { frac { cos epsilon} { omega}} right] _ {E}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9aee5c61b772a72ee2d7612aabe1d8bc3c3dfc4)


