Законы Кеплера движения планет - Википедия - Keplers laws of planetary motion

Рисунок 1: Иллюстрация трех законов Кеплера с двумя планетными орбитами.

Орбиты - эллипсы, с фокусами F₁ и F₂ для первой планеты и F₁ и F₃ для второй планеты. Солнце находится в фокусе F₁.
Два заштрихованных сектора А₁ и А₂ имеют одинаковую площадь поверхности и время, за которое планета 1 покрывает сегмент А₁ равно времени прохождения сегмента А₂.
Полное время обращения планеты 1 и планеты 2 имеет соотношение ${ textstyle left ({ frac {a_ {1}} {a_ {2}}} right) ^ { frac {3} {2}}}$ .

В астрономия, Законы движения планет Кеплера, опубликовано Иоганн Кеплер между 1609 и 1619 годами, опишите орбиты планеты вокруг солнце. Законы изменили гелиоцентрическая теория из Николай Коперник, заменив его циркулярный орбиты и эпициклы с эллиптическими траекториями и объясняя, как меняются скорости планет. Эти три закона гласят:

Орбита планеты - это эллипс с Солнцем в одном из двух фокусов.
Отрезок, соединяющий планету и Солнце, сметает равные области за равные промежутки времени.
Квадрат планеты орбитальный период пропорциональна кубу длины большая полуось своей орбиты.

Эллиптические орбиты планет указывались расчетами орбиты планет. Марс. Из этого Кеплер сделал вывод, что другие тела в Солнечная система, в том числе и те, что дальше от Солнца, также имеют эллиптические орбиты. Второй закон помогает установить, что, когда планета находится ближе к Солнцу, она движется быстрее. Третий закон гласит, что чем дальше планета от Солнца, тем медленнее ее орбитальная скорость, и наоборот.

Исаак Ньютон показал в 1687 году, что отношения, подобные соотношению Кеплера, применимы в Солнечной системе с хорошим приближением, как следствие его собственного законы движения и закон всемирного тяготения.

Сравнение с коперником

Иоганн Кеплер российские законы улучшили модель Коперника. Если эксцентриситет планетарного орбиты приняты за ноль, то Кеплер в основном согласился с Коперником:

Планетарная орбита представляет собой круг.
Солнце находится в центре орбиты.
Скорость планеты на орбите постоянна.

Эксцентриситеты орбит планет, известных Копернику и Кеплеру, невелики, поэтому вышеприведенные правила дают хорошее приближение движения планет, но законы Кеплера лучше подходят для наблюдений, чем модель, предложенная Коперником. Поправки Кеплера:

Планетарная орбита нет круг, но эллипс.
Солнце это нет в центре, но в координационный центр эллиптической орбиты.
Ни линейная скорость, ни угловая скорость планеты на орбите не постоянны, но скорость по площади (исторически тесно связаны с концепцией угловой момент ) постоянна.

Неординарность орбита Земли делает время из Мартовское равноденствие к Сентябрьское равноденствие, около 186 дней, что не соответствует времени от сентябрьского равноденствия до мартовского равноденствия, около 179 дней. Диаметр разрезал бы орбиту на равные части, но плоскость, проходящая через Солнце, параллельна экватор Земли разделяет орбиту на две части с областями в соотношении 186 к 179, так что эксцентриситет орбиты Земли приблизительно равен

{ displaystyle e приблизительно { frac { pi} {4}} { frac {186-179} {186 + 179}} приблизительно 0,015,}

что близко к правильному значению (0,016710218). Точность этого расчета требует, чтобы две выбранные даты располагались вдоль малой оси эллиптической орбиты, а средние точки каждой половины - вдоль большой оси. Поскольку две выбранные здесь даты - равноденствия, это будет правильно, когда перигелий, дата, когда Земля находится ближе всего к Солнцу, приходится на солнцестояние. Текущий перигелий около 4 января довольно близок к солнцестоянию 21 или 22 декабря.

Номенклатура

Потребовалось почти два столетия, чтобы нынешняя формулировка работы Кеплера приняла устойчивую форму. Вольтер с Элементы философии Ньютона (Элементы философии Ньютона) 1738 г. было первым изданием, в котором использовалась терминология «законы».^[1]^[2] В Биографическая энциклопедия астрономов в своей статье о Кеплере (стр. 620) заявляет, что терминология научных законов для этих открытий была актуальной, по крайней мере, со времен Жозеф де Лаланд.^[3] Это была экспозиция Роберт Смолл, в Отчет об астрономических открытиях Кеплера (1814 г.), которые составили свод из трех законов, добавив третий.^[4] Смолл также утверждал, вопреки истории, что это были эмпирические законы, на основе индуктивное мышление.^[2]^[5]

Более того, нынешнее использование «Второго закона Кеплера» в некоторой степени неверно. У Кеплера было две версии, взаимосвязанные в качественном смысле: «закон расстояния» и «закон площади». «Закон области» - это то, что стало Вторым Законом из набора из трех; но сам Кеплер не придавал этому особого значения.^[6]

История

Кеплер опубликовал свои первые два закона о движении планет в 1609 году.^[7] обнаружив их, проанализировав астрономические наблюдения Тихо Браге.^[8]^[9]^[10] Третий закон Кеплера был опубликован в 1619 году.^[11]^[9] Кеплер верил в Коперниканская модель Солнечной системы, которая требовала круговых орбит, но он не мог согласовать высокоточные наблюдения Браге с круговой аппроксимацией орбиты Марса - Марс по совпадению имел самый высокий эксцентриситет из всех планет, кроме Меркурия.^[12] Его первый закон отразил это открытие.

В 1621 году Кеплер отметил, что его третий закон применим к четыре самых ярких луны из Юпитер.^{[Nb 1]} Годфрой Венделин также сделал это наблюдение в 1643 году.^{[Nb 2]} Второй закон в форме «закона о территории» был оспорен Николаус Меркатор в книге 1664 года, но к 1670 году его Философские труды были в ее пользу. По прошествии века это стало более широко распространенным.^[13] Прием в Германии заметно изменился между 1688 годом, когда Ньютон Principia был опубликован и считался в основном коперниканским, а в 1690 г. Готфрид Лейбниц о Кеплере.^[14]

Ньютону приписывали понимание того, что второй закон не является частным по отношению к закону обратных квадратов гравитации, а является следствием радиальной природы этого закона; в то время как другие законы зависят от формы обратных квадратов притяжения. Карл Рунге и Вильгельм Ленц намного позже идентифицировал принцип симметрии в фазовое пространство планетарного движения ( ортогональная группа O (4) действие), который учитывает первый и третий законы в случае ньютоновской гравитации, как сохранение углового момента делает через вращательную симметрию для второго закона.^[15]

Формуляр

Математическая модель кинематики планеты, подчиняющейся законам, допускает большой диапазон дальнейших вычислений.

Первый закон

Орбита каждой планеты представляет собой эллипс с Солнцем в одном из двух фокусы.

Рисунок 2: Первый закон Кеплера, помещающий Солнце в фокус эллиптической орбиты

Рисунок 4: Гелиоцентрическая система координат (р, θ) для эллипса. Также показаны: большая полуось а, малая полуось б и полу-латусная прямая кишка п; центр эллипса и два его фокуса отмечены большими точками. За θ = 0 °, р = р_мин и для θ = 180 °, р = р_{Максимум}.

Математически эллипс можно представить формулой:

{ displaystyle r = { frac {p} {1+ varepsilon , cos theta}},}

куда ${ displaystyle p}$ это полу-латусная прямая кишка, ε - эксцентриситет эллипса, р это расстояние от Солнца до планеты, а θ - это угол к текущему положению планеты с точки зрения ближайшего приближения, если смотреть со стороны Солнца. Так (р, θ) находятся полярные координаты.

Для эллипса 0 <ε <1; в предельном случае ε = 0, орбита представляет собой круг с Солнцем в центре (то есть там, где нет эксцентриситета).

В θ = 0°, перигелий, расстояние минимальное

{ displaystyle r _ { min} = { frac {p} {1+ varepsilon}}}

В θ = 90 ° и при θ = 270 ° расстояние равно ${ displaystyle p}$ .

В θ = 180°, афелий, расстояние максимальное (по определению афелий - обязательно перигелий плюс 180 °)

{ displaystyle r _ { max} = { frac {p} {1- varepsilon}}}

В большая полуось а это среднее арифметическое между р_мин и р_{Максимум}:

{ displaystyle { begin {align} r _ { max} -a & = a-r _ { min} [3pt] a & = { frac {p} {1- varepsilon ^ {2}}} end {выровнено}}}

В малая полуось б это среднее геометрическое между р_мин и р_{Максимум}:

{ displaystyle { begin {align} { frac {r _ { max}} {b}} & = { frac {b} {r _ { min}}} [3pt] b & = { frac { p} { sqrt {1- varepsilon ^ {2}}}} конец {выровнено}}}

Полу-латусная прямая кишка п это гармоническое среднее между р_мин и р_{Максимум}:

{ displaystyle { begin {align} { frac {1} {r _ { min}}} - { frac {1} {p}} & = { frac {1} {p}} - { frac {1} {r _ { max}}} [3pt] pa & = r _ { max} r _ { min} = b ^ {2} , end {align}}}

Эксцентричность ε это коэффициент вариации между р_мин и р_{Максимум}:

{ displaystyle varepsilon = { frac {r _ { max} -r _ { min}} {r _ { max} + r _ { min}}}.}

В площадь эллипса

{ displaystyle A = pi ab ,.}

Частным случаем круга является ε = 0, в результате р = п = р_мин = р_{Максимум} = а = б и А = πr².

Второй закон

А линия присоединяясь к планете, Солнце сметает равные области за равные промежутки времени.^[16]

Та же (синяя) область выметается за фиксированный период времени. Зеленая стрелка - скорость. Фиолетовая стрелка, направленная к Солнцу, - это ускорение. Две другие фиолетовые стрелки - это компоненты ускорения, параллельные и перпендикулярные скорости.

Радиус орбиты и угловая скорость планеты на эллиптической орбите будут изменяться. Это показано на анимации: планета движется быстрее, когда приближается к Солнцу, и медленнее, когда дальше от Солнца. Второй закон Кеплера гласит, что синий сектор имеет постоянную площадь.

За короткое время ${ displaystyle dt ,}$ планета выметает маленький треугольник с базовой линией ${ displaystyle r}$ и высота ${ Displaystyle г , д тета}$ и площадь ${ displaystyle dA = { frac {1} {2}} cdot r cdot r , d theta}$ , поэтому постоянная площадная скорость является ${ displaystyle { frac {dA} {dt}} = { frac {r ^ {2}} {2}} { frac {d theta} {dt}}.}$

Площадь, ограниченная эллиптической орбитой, равна ${ displaystyle pi ab. ,}$ Итак, период ${ displaystyle P}$ удовлетворяет

{ displaystyle P cdot { frac {r ^ {2}} {2}} { frac {d theta} {dt}} = pi ab}

и среднее движение планеты вокруг Солнца

{ Displaystyle п = { гидроразрыва {2 pi} {P}}}

удовлетворяет

{ Displaystyle г ^ {2} , d theta = abn , dt.}

Третий закон

Отношение площади объекта к орбитальный период с кубом большой полуоси его орбиты одинаков для всех объектов, вращающихся вокруг одной и той же главной оси.

Это отражает взаимосвязь между расстоянием планет от Солнца и их орбитальными периодами.

Кеплер провозгласил в 1619 году^[11] этот третий закон в кропотливой попытке определить, что он считал "музыка сфер "согласно точным законам, и выразить это в нотной записи.^[17] Так он был известен как гармонический закон.^[18]

Используя закон всемирного тяготения Ньютона (опубликованный в 1687 г.), это соотношение можно найти в случае круговой орбиты, задав центростремительная сила равна силе тяжести:

{ displaystyle mr omega ^ {2} = G { frac {mM} {r ^ {2}}}}

Затем, выражая угловую скорость через период обращения и затем перестраивая, мы находим Третий закон Кеплера:

{ displaystyle mr left ({ frac {2 pi} {T}} right) ^ {2} = G { frac {mM} {r ^ {2}}} rightarrow T ^ {2} = left ({ frac {4 pi ^ {2}} {GM}} right) r ^ {3} rightarrow T ^ {2} propto r ^ {3}}

Более подробный вывод может быть выполнен с использованием общих эллиптических орбит вместо кругов, а также с вращением вокруг центра масс, а не просто с большой массой. Это приводит к замене круглого радиуса, ${ displaystyle r}$ , с большой полуосью, ${ displaystyle a}$ , эллиптического относительного движения одной массы относительно другой, а также замены большой массы ${ displaystyle M}$ с ${ displaystyle M + m}$ . Однако, поскольку массы планет намного меньше Солнца, эту поправку часто игнорируют. Полная соответствующая формула:

{ displaystyle { frac {a ^ {3}} {T ^ {2}}} = { frac {G (M + m)} {4 pi ^ {2}}} приблизительно { frac {GM } {4 pi ^ {2}}} приблизительно 7,496 cdot 10 ^ {- 6} left ({ frac {{ text {AU}} ^ {3}} {{ text {days}} ^ {2}}} right) { text {константа}}}

куда ${ displaystyle M}$ это масса Солнца, ${ displaystyle m}$ масса планеты, ${ displaystyle G}$ это гравитационная постоянная, ${ displaystyle T}$ это период обращения и ${ displaystyle a}$ - большая полуось эллипса, а ${ displaystyle { text {AU}}}$ это Астрономический блок, среднее расстояние от Земли до Солнца.

В следующей таблице показаны данные, которые использовал Кеплер для эмпирического вывода своего закона:

Данные, использованные Кеплером (1618 г.)
Планета	Среднее расстояние к солнцу (AU)	Период (дней)	${ textstyle { frac {R ^ {3}} {T ^ {2}}}}$ (10^-6 AU³/день²)
Меркурий	0.389	87.77	7.64
Венера	0.724	224.70	7.52
земной шар	1	365.25	7.50
Марс	1.524	686.95	7.50
Юпитер	5.2	4332.62	7.49
Сатурн	9.510	10759.2	7.43

Обнаружив этот образец, Кеплер написал:^[19]

Сначала я поверил, что я сплю ... Но совершенно точно и ясно, что соотношение, которое существует между периодами периодов любых двух планет, в точности равно соотношению 3/2 степени среднего расстояния.
— переведено с Гармонии Мира по Кеплеру (1619)

Логарифмический график большой полуоси (в астрономических единицах) по сравнению с периодом обращения (в земных годах) для восьми планет Солнечной системы.

Для сравнения - современные оценки:

Современные данные (база знаний Wolfram Alpha 2018)
Планета	Большая полуось (AU)	Период (дни)	${ textstyle { frac {R ^ {3}} {T ^ {2}}}}$ (10^-6 AU³/день²)
Меркурий	0.38710	87.9693	7.496
Венера	0.72333	224.7008	7.496
земной шар	1	365.2564	7.496
Марс	1.52366	686.9796	7.495
Юпитер	5.20336	4332.8201	7.504
Сатурн	9.53707	10775.599	7.498
Уран	19.1913	30687.153	7.506
Нептун	30.0690	60190.03	7.504

Планетарное ускорение

Исаак Ньютон вычислено в его Philosophiæ Naturalis Principia Mathematica то ускорение планеты, движущейся согласно первому и второму закону Кеплера.

В направление ускорения направлено к Солнцу.
В величина ускорения обратно пропорционально квадрату расстояния планеты от Солнца ( закон обратных квадратов).

Это означает, что Солнце может быть физической причиной ускорения планет. Однако Ньютон утверждает в своем Principia что он рассматривает силы с математической, а не физической точки зрения, тем самым принимая инструменталистскую точку зрения.^[20] Более того, он не приписывает гравитации причину.^[21]

Ньютон определил сила действует на планете, чтобы быть продуктом ее масса и ускорение (см. Законы движения Ньютона ). Так:

Каждая планета тянется к Солнцу.
Сила, действующая на планету, прямо пропорциональна массе планеты и обратно пропорциональна квадрату ее расстояния от Солнца.

Солнце играет несимметричную роль, что неоправданно. Так он предположил, что в Закон всемирного тяготения Ньютона:

Все тела в Солнечной системе притягиваются друг к другу.
Сила между двумя телами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.

Поскольку массы планет малы по сравнению с массой Солнца, их орбиты приблизительно соответствуют законам Кеплера. Модель Ньютона улучшает модель Кеплера и более точно соответствует реальным наблюдениям (см. проблема двух тел ).

Ниже приводится подробный расчет ускорения планеты, движущейся согласно первому и второму законам Кеплера.

Вектор ускорения

От гелиоцентрический с точки зрения рассмотрим вектор к планете ${ displaystyle mathbf {r} = r { hat { mathbf {r}}}}$ куда ${ displaystyle r}$ это расстояние до планеты и ${ displaystyle { hat { mathbf {r}}}}$ это единичный вектор указывая на планету.

{ displaystyle { frac {d { hat { mathbf {r}}}} {dt}} = { dot { hat { mathbf {r}}}} = { dot { theta}} { hat { boldsymbol { theta}}}, qquad { frac {d { hat { boldsymbol { theta}}}} {dt}} = { dot { hat { boldsymbol { theta} }}} = - { dot { theta}} { hat { mathbf {r}}}}

куда ${ displaystyle { hat { boldsymbol { theta}}}}$ - единичный вектор, направление которого составляет 90 градусов против часовой стрелки от ${ displaystyle { hat { mathbf {r}}}}$ , и ${ displaystyle theta}$ - полярный угол, а где a точка сверху переменной означает дифференциацию по времени.

Дважды дифференцируйте вектор положения, чтобы получить вектор скорости и вектор ускорения:

{ displaystyle { begin {align} { dot { mathbf {r}}} & = { dot {r}} { hat { mathbf {r}}} + r { dot { hat { mathbf {r}}}} = { dot {r}} { hat { mathbf {r}}} + r { dot { theta}} { hat { boldsymbol { theta}}}, { ddot { mathbf {r}}} & = left ({ ddot {r}} { hat { mathbf {r}}} + { dot {r}} { dot { hat { mathbf {r}}}} right) + left ({ dot {r}} { dot { theta}} { hat { boldsymbol { theta}}} + r { ddot { theta }} { hat { boldsymbol { theta}}} + r { dot { theta}} { dot { hat { boldsymbol { theta}}}} right) = left ({ ddot {r}} - r { dot { theta}} ^ {2} right) { hat { mathbf {r}}} + left (r { ddot { theta}} + 2 { dot {r}} { dot { theta}} right) { hat { boldsymbol { theta}}}. end {align}}}

Так

{ displaystyle { ddot { mathbf {r}}} = a_ {r} { hat { boldsymbol {r}}} + a _ { theta} { hat { boldsymbol { theta}}}}

где радиальное ускорение является

{ displaystyle a_ {r} = { ddot {r}} - r { dot { theta}} ^ {2}}

и поперечное ускорение является

{ displaystyle a _ { theta} = r { ddot { theta}} + 2 { dot {r}} { dot { theta}}.}

Закон обратных квадратов

Второй закон Кеплера гласит, что

{ Displaystyle г ^ {2} { точка { theta}} = наб}

постоянно.

Поперечное ускорение ${ displaystyle a _ { theta}}$ равно нулю:

{ displaystyle { frac {d left (r ^ {2} { dot { theta}} right)} {dt}} = r left (2 { dot {r}} { dot { theta}} + r { ddot { theta}} right) = ra _ { theta} = 0.}

Итак, ускорение планеты, подчиняющейся второму закону Кеплера, направлено к Солнцу.

Радиальное ускорение ${ displaystyle a _ { text {r}}}$ является

{ displaystyle a _ { text {r}} = { ddot {r}} - r { dot { theta}} ^ {2} = { ddot {r}} - r left ({ frac { nab} {r ^ {2}}} right) ^ {2} = { ddot {r}} - { frac {n ^ {2} a ^ {2} b ^ {2}} {r ^ { 3}}}.}

Первый закон Кеплера гласит, что орбита описывается уравнением:

{ displaystyle { frac {p} {r}} = 1+ varepsilon cos ( theta).}

Дифференциация по времени

{ displaystyle - { frac {p { dot {r}}} {r ^ {2}}} = - varepsilon sin ( theta) , { dot { theta}}}

или же

{ displaystyle p { dot {r}} = nab , varepsilon sin ( theta).}

Еще раз дифференцируя

{ Displaystyle п { ddot {r}} = nab varepsilon cos ( theta) , { dot { theta}} = nab varepsilon cos ( theta) , { frac {nab} { r ^ {2}}} = { frac {n ^ {2} a ^ {2} b ^ {2}} {r ^ {2}}} varepsilon cos ( theta).}

Радиальное ускорение ${ displaystyle a _ { text {r}}}$ удовлетворяет

{ displaystyle pa _ { text {r}} = { frac {n ^ {2} a ^ {2} b ^ {2}} {r ^ {2}}} varepsilon cos ( theta) -p { frac {n ^ {2} a ^ {2} b ^ {2}} {r ^ {3}}} = { frac {n ^ {2} a ^ {2} b ^ {2}} { r ^ {2}}} left ( varepsilon cos ( theta) - { frac {p} {r}} right).}

Подстановка уравнения эллипса дает

{ displaystyle pa _ { text {r}} = { frac {n ^ {2} a ^ {2} b ^ {2}} {r ^ {2}}} left ({ frac {p} { r}} - 1 - { frac {p} {r}} right) = - { frac {n ^ {2} a ^ {2}} {r ^ {2}}} b ^ {2}. }

Соотношение ${ displaystyle b ^ {2} = pa}$ дает простой конечный результат

{ displaystyle a _ { text {r}} = - { frac {n ^ {2} a ^ {3}} {r ^ {2}}}.}

Это означает, что вектор ускорения ${ Displaystyle mathbf { ddot {r}}}$ любой планеты, подчиняющейся первому и второму закону Кеплера, удовлетворяет закон обратных квадратов

{ displaystyle mathbf { ddot {r}} = - { frac { alpha} {r ^ {2}}} { hat { mathbf {r}}}}

куда

{ Displaystyle альфа = п ^ {2} а ^ {3} ,}

константа, а ${ displaystyle { hat { mathbf {r}}}}$ - единичный вектор, направленный от Солнца к планете, и ${ Displaystyle г ,}$ это расстояние между планетой и Солнцем.

Поскольку среднее движение ${ Displaystyle п = { гидроразрыва {2 pi} {T}}}$ куда ${ displaystyle T}$ - период, согласно третьему закону Кеплера, ${ displaystyle alpha}$ имеет одинаковое значение для всех планет. Таким образом, закон обратных квадратов для планетных ускорений применим ко всей Солнечной системе.

Закон обратных квадратов - это дифференциальное уравнение. Решения этого дифференциального уравнения включают в себя кеплеровские движения, как показано, но они также включают движения, в которых орбита является гипербола или же парабола или прямая линия. Видеть Орбита Кеплера.

Закон всемирного тяготения Ньютона

К Второй закон Ньютона, гравитационная сила, действующая на планету, равна:

{ displaystyle mathbf {F} = m _ { text {planet}} mathbf { ddot {r}} = -m _ { text {planet}} alpha r ^ {- 2} { hat { mathbf {р} }}}

куда ${ displaystyle m _ { text {planet}}}$ масса планеты и ${ displaystyle alpha}$ имеет одинаковое значение для всех планет Солнечной системы. В соответствии с Третий закон Ньютона, Солнце притягивается к планете силой той же величины. Поскольку сила пропорциональна массе планеты, при симметричном рассмотрении она также должна быть пропорциональна массе Солнца, ${ displaystyle m _ { text {солнце}}}$ . Так

{ displaystyle alpha = Gm _ { text {солнце}}}

куда ${ displaystyle G}$ это гравитационная постоянная.

Ускорение числа тел Солнечной системы я составляет по законам Ньютона:

{ displaystyle mathbf { ddot {r}} _ {i} = G sum _ {j neq i} m_ {j} r_ {ij} ^ {- 2} { hat { mathbf {r}} } _ {ij}}

куда ${ displaystyle m_ {j}}$ это масса тела j, ${ displaystyle r_ {ij}}$ это расстояние между телами я и тело j, ${ displaystyle { hat { mathbf {r}}} _ {ij}}$ это единичный вектор от тела я к телу j, а векторное суммирование ведется по всем телам Солнечной системы, кроме я сам.

В частном случае, когда в Солнечной системе всего два тела, Земля и Солнце, ускорение становится равным

{ displaystyle mathbf { ddot {r}} _ { text {Earth}} = Gm _ { text {Sun}} r _ {{ text {Earth}}, { text {Sun}}} ^ {- 2} { hat { mathbf {r}}} _ {{ text {Земля}}, { text {Солнце}}}}

что является ускорением движения Кеплера. Итак, эта Земля движется вокруг Солнца согласно законам Кеплера.

Если два тела в Солнечной системе - Луна и Земля, ускорение Луны становится равным

{ displaystyle mathbf { ddot {r}} _ { text {Moon}} = Gm _ { text {Earth}} r _ {{ text {Moon}}, { text {Earth}}} ^ {- 2} { hat { mathbf {r}}} _ {{ text {Луна}}, { text {Земля}}}}

Итак, в этом приближении Луна движется вокруг Земли по законам Кеплера.

В трехчастном случае ускорения равны

{ displaystyle { begin {align} mathbf { ddot {r}} _ { text {Sun}} & = Gm _ { text {Earth}} r _ {{ text {Sun}}, { text { Земля}}} ^ {- 2} { hat { mathbf {r}}} _ {{ text {Sun}}, { text {Earth}}} + Gm _ { text {Moon}} r _ {{ text {Солнце}}, { text {Луна}}} ^ {- 2} { hat { mathbf {r}}} _ {{ text {Солнце}}, { text {Луна}}} mathbf { ddot {r}} _ { text {Земля}} & = Gm _ { text {Sun}} r _ {{ text {Earth}}, { text {Sun}}} ^ {- 2 } { hat { mathbf {r}}} _ {{ text {Earth}}, { text {Sun}}} + Gm _ { text {Moon}} r _ {{ text {Earth}}, { text {Луна}}} ^ {- 2} { hat { mathbf {r}}} _ {{ text {Земля}}, { text {Moon}}} mathbf { ddot {r }} _ { text {Moon}} & = Gm _ { text {Sun}} r _ {{ text {Moon}}, { text {Sun}}} ^ {- 2} { hat { mathbf { r}}} _ {{ text {Moon}}, { text {Sun}}} + Gm _ { text {Earth}} r _ {{ text {Moon}}, { text {Earth}}} ^ {-2} { hat { mathbf {r}}} _ {{ text {Луна}}, { text {Земля}}} end {align}}}

Эти ускорения не являются ускорениями орбит Кеплера, и проблема трех тел это сложно. Но кеплеровское приближение лежит в основе возмущение расчеты. Видеть Лунная теория.

Положение как функция времени

Кеплер использовал свои два первых закона для вычисления положения планеты как функции времени. Его метод предполагает решение трансцендентное уравнение называется Уравнение Кеплера.

Процедура расчета гелиоцентрических полярных координат (р,θ) планеты как функция времени т поскольку перигелий, это следующие пять шагов:

Вычислить среднее движение п = (2 $π$ радианы) /п, куда п это период.
Вычислить средняя аномалия M = нт, куда т это время с перилгелия.
Вычислить эксцентрическая аномалия E путем решения уравнения Кеплера:
${ Displaystyle M = E- varepsilon sin E}$ , куда ${ displaystyle varepsilon}$ это эксцентриситет.
Вычислить истинная аномалия θ путем решения уравнения:
${ Displaystyle (1- varepsilon) tan ^ {2} { frac { theta} {2}} = (1+ varepsilon) tan ^ {2} { frac {E} {2}}}$
Вычислить гелиоцентрическое расстояние р:
${ Displaystyle г = а (1- varepsilon cos E)}$ , куда ${ displaystyle a}$ - большая полуось.

Тогда вектор декартовой скорости можно рассчитать как ${ displaystyle mathbf {v} = { frac { sqrt { mu a}} {r}} left langle - sin {E}, { sqrt {1- varepsilon ^ {2}}} cos {E} right rangle}$ , куда ${ displaystyle mu}$ это стандартный гравитационный параметр.^[22]

Важный частный случай круговой орбиты, ε = 0, дает θ = E = M. Поскольку равномерное круговое движение считалось нормальныйотклонение от этого движения считалось аномалия.

Доказательство этой процедуры показано ниже.

Средняя аномалия, M

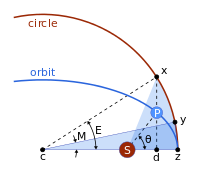
Рисунок 5: Геометрическая конструкция для вычисления θ Кеплером. Солнце (находится в фокусе) помечено S и планета п. Вспомогательный кружок - помощь в расчетах. Линия xd перпендикулярно основанию и через планету п. Заштрихованные секторы располагаются на равных площадях за счет расположения точки у.

Кеплеровская проблема предполагает эллиптическая орбита и четыре точки:

s Солнце (в одном фокусе эллипса);

z то перигелий

c центр эллипса

п планета

и

{ Displaystyle а = | cz |,}

расстояние между центром и перигелием, большая полуось,

{ displaystyle varepsilon = {| cs | через},}

то эксцентриситет,

{ Displaystyle B = а { sqrt {1- varepsilon ^ {2}}},}

то малая полуось,

{ displaystyle r = | sp |,}

расстояние между Солнцем и планетой.

{ displaystyle theta = angle zsp,}

направление на планету, если смотреть со стороны Солнца, истинная аномалия.

Проблема состоит в том, чтобы вычислить полярные координаты (р,θ) планеты из время с перигелия, т.

Решается поэтапно. Кеплер считал круг с большой осью диаметром, а

{ displaystyle x,}

проекция планеты на вспомогательный круг

{ displaystyle y,}

точка на окружности такая, что площади сектора |zcy| и |zsx| равны,

{ Displaystyle M = угол zcy,}

то средняя аномалия.

Секторные области связаны между собой ${ displaystyle | zsp | = { frac {b} {a}} cdot | zsx |.}$

В круговой сектор площадь ${ displaystyle | zcy | = { frac {a ^ {2} M} {2}}.}$

Площадь заметна с перигелия,

{ displaystyle | zsp | = { frac {b} {a}} cdot | zsx | = { frac {b} {a}} cdot | zcy | = { frac {b} {a}} cdot { frac {a ^ {2} M} {2}} = { frac {abM} {2}},}

согласно второму закону Кеплера пропорциональна времени, прошедшему с перигелия. Итак, средняя аномалия, M, пропорционально времени, прошедшему с перигелия, т.

{ Displaystyle M = nt, ,}

куда п это среднее движение.

Эксцентрическая аномалия, E

Когда средняя аномалия M вычисляется, цель состоит в том, чтобы вычислить истинную аномалию θ. Функция θ = ж(M), однако, не является элементарным.^[23] Решение Кеплера заключается в использовании

{ displaystyle E = angle zcx}

, Икс если смотреть из центра, эксцентрическая аномалия

в качестве промежуточной переменной и сначала вычислить E как функция M решив приведенное ниже уравнение Кеплера, а затем вычислите истинную аномалию θ от эксцентрической аномалии E. Вот подробности.

{ displaystyle { begin {align} | zcy | & = | zsx | = | zcx | - | scx | { frac {a ^ {2} M} {2}} & = { frac {a ^ {2} E} {2}} - { frac {a varepsilon cdot a sin E} {2}} end {align}}}

Деление по а²/ 2 дает Уравнение Кеплера

{ Displaystyle M = E- varepsilon sin E.}

Это уравнение дает M как функция E. Определение E для данного M - обратная задача. Обычно используются итерационные численные алгоритмы.

Вычислив эксцентрическую аномалию E, следующим шагом будет вычисление истинной аномалииθ.

Но обратите внимание: декартовы координаты положения относительно центра эллипса равны (а потому чтоE, б грехE)

Ссылка на Солнце (с координатами (c,0) = (ае,0) ), р = (а потому чтоE – ае, б грехE)

Истинная аномалия была бы арктана (р_у/рИкс), величина р было бы √р · р.

Истинная аномалия, θ

Обратите внимание на рисунок, что

{ displaystyle { overrightarrow {cd}} = { overrightarrow {cs}} + { overrightarrow {sd}}}

так что

{ displaystyle a cos E = a varepsilon + r cos theta.}

Деление на ${ displaystyle a}$ и вставляя из первого закона Кеплера

{ displaystyle { frac {r} {a}} = { frac {1- varepsilon ^ {2}} {1+ varepsilon cos theta}}}

получить

{ displaystyle cos E = varepsilon + { frac {1- varepsilon ^ {2}} {1+ varepsilon cos theta}} cos theta = { frac { varepsilon (1+ varepsilon cos theta) + left (1- varepsilon ^ {2} right) cos theta} {1+ varepsilon cos theta}} = { frac { varepsilon + cos theta} { 1+ varepsilon cos theta}}.}

Результатом является полезная связь между эксцентрической аномалией. E и настоящая аномалияθ.

В вычислительном отношении более удобная форма получается заменой в тригонометрическая идентичность:

{ displaystyle tan ^ {2} { frac {x} {2}} = { frac {1- cos x} {1+ cos x}}.}

Получать

{ displaystyle { begin {align} tan ^ {2} { frac {E} {2}} & = { frac {1- cos E} {1+ cos E}} = { frac { 1 - { frac { varepsilon + cos theta} {1+ varepsilon cos theta}}} {1 + { frac { varepsilon + cos theta} {1+ varepsilon cos theta }}}} [8pt] & = { frac {(1+ varepsilon cos theta) - ( varepsilon + cos theta)} {(1+ varepsilon cos theta) + ( varepsilon + cos theta)}} = { frac {1- varepsilon} {1+ varepsilon}} cdot { frac {1- cos theta} {1+ cos theta}} = { frac {1- varepsilon} {1+ varepsilon}} tan ^ {2} { frac { theta} {2}}. end {align}}}

Умножение на 1 +ε дает результат

{ Displaystyle (1- varepsilon) tan ^ {2} { frac { theta} {2}} = (1+ varepsilon) tan ^ {2} { frac {E} {2}}}

Это третий шаг в связи между временем и положением на орбите.

Расстояние, р

Четвертый шаг - вычислить гелиоцентрическое расстояние р от истинной аномалии θ по первому закону Кеплера:

{ Displaystyle г (1+ varepsilon cos theta) = а влево (1- varepsilon ^ {2} right)}

Используя указанное выше соотношение между θ и E окончательное уравнение для расстояния р является:

{ displaystyle r = a (1- varepsilon cos E).}

Смотрите также

Круговое движение
Время свободного падения
Сила тяжести
Орбита Кеплера
Проблема Кеплера
Уравнение Кеплера
Вектор Лапласа – Рунге – Ленца.
Удельный относительный угловой момент, относительно простой вывод законов Кеплера, начиная с сохранения углового момента

Примечания

^ В 1621 году Иоганн Кеплер отметил, что эти луны подчиняются (приблизительно) его третьему закону в своей книге. Epitome Astronomiae Copernicanae [Воплощение коперниканской астрономии] (Линц ("Lentiis ad Danubium"), (Австрия): Иоганн Планк, 1622), книга 4, часть 2, стр. 554.
^ Годфрой Венделин написал письмо Джованни Баттиста Риччоли о взаимосвязи между расстояниями спутников Юпитера от Юпитера и периодами их орбит, показывая, что периоды и расстояния соответствуют третьему закону Кеплера. См .: Джоан Баптиста Риччоли, Альмагестум новум ... (Болонья (Бонония), (Италия): Виктор Бенати, 1651), том 1, стр. 492 Схолия III. На полях рядом с соответствующим абзацем напечатано: Vendelini ingeniosa speculatio около motus & intervalla satellitum Jovis. (Умное предположение Венделина о движении и расстояниях до спутников Юпитера.)

Библиография

Жизнь Кеплера кратко описана на страницах 523–627 и в пятой книге его magnum opus, Harmonice Mundi (гармонии мира), перепечатывается на страницах 635–732 На плечах гигантов: Великие труды по физике и астрономии (сочинения Коперника, Кеплер, Галилео, Ньютон, и Эйнштейн ). Стивен Хокинг, изд. 2002 г. ISBN 0-7624-1348-4
Вывод третьего закона движения планет Кеплера - стандартная тема на уроках инженерной механики. См., Например, страницы 161–164 Мериам, Дж. Л. (1971) [1966]. Динамика, 2-е изд.. Нью-Йорк: Джон Вили. ISBN 978-0-471-59601-1..
Мюррей и Дермотт, Динамика солнечной системы, Cambridge University Press, 1999, ISBN 0-521-57597-4
В.И. Арнольд, Математические методы классической механики, глава 2. Springer 1989, ISBN 0-387-96890-3

внешняя ссылка

Б. Сурендранат Редди; анимация законов Кеплера: апплет
"Вывод законов Кеплера. "(из законов Ньютона) при Обмен физическими стеками.
Кроуэлл, Бенджамин, Свет и материя, онлайн-книга который дает доказательство первого закона без использования исчисления (см. раздел 15.7)
Дэвид Макнамара и Джанфранко Видали, Второй закон Кеплера - Интерактивное руководство по Java, https://web.archive.org/web/20060910225253/http://www.phy.syr.edu/courses/java/mc_html/kepler.html, интерактивный Java-апплет, который помогает понять Второй закон Кеплера.
Аудио - Каин / Гей (2010) Астрономический состав Иоганн Кеплер и его законы движения планет
Университет Теннесси, факультет физики и астрономии: астрономия, 161 страница, посвященная Иоганну Кеплеру: законы движения планет [1]
Equant по сравнению с Kepler: интерактивная модель [2]
Третий закон Кеплера: интерактивная модель [3]
Симулятор солнечной системы (Интерактивный апплет )
Кеплер и его законы, образовательные веб-страницы Дэвида П. Стерна

[13] В 1621 году Иоганн Кеплер отметил, что эти луны подчиняются (приблизительно) его третьему закону в своей книге. Epitome Astronomiae Copernicanae [Воплощение коперниканской астрономии] (Линц ("Lentiis ad Danubium"), (Австрия): Иоганн Планк, 1622), книга 4, часть 2, стр. 554.

[14] Годфрой Венделин написал письмо Джованни Баттиста Риччоли о взаимосвязи между расстояниями спутников Юпитера от Юпитера и периодами их орбит, показывая, что периоды и расстояния соответствуют третьему закону Кеплера. См .: Джоан Баптиста Риччоли, Альмагестум новум ... (Болонья (Бонония), (Италия): Виктор Бенати, 1651), том 1, стр. 492 Схолия III. На полях рядом с соответствующим абзацем напечатано: Vendelini ingeniosa speculatio около motus & intervalla satellitum Jovis. (Умное предположение Венделина о движении и расстояниях до спутников Юпитера.)

[1] Вольтер, Элементы философии Ньютона [Элементы философии Ньютона] (Лондон, Англия: 1738). См. Например:
С п. 162: "Par une des grandes loix de Kepler, toute Planete décrit des aires égales en temp égaux: par une autre loi non-moins sûre, chaque Planete fait sa révolution autour du Soleil en telle sort, que si, sa moyenne distance au Soleil est 10 . prenez le cube de ce nombre, ce qui sera 1000., & le tems de la révolution de cette Planete autour du Soleil sera пропорционально à la racine qurée de ce nombre 1000 ". (Согласно одному из великих законов Кеплера каждая планета описывает равные площади в равное время; согласно другому, не менее определенному закону, каждая планета совершает свой оборот вокруг Солнца таким образом, что если ее среднее расстояние от Солнца равно 10, куб этого числа, которое будет равно 1000, и время обращения этой планеты вокруг Солнца будет пропорционально квадратному корню из этого числа 1000.)
С п. 205: "Il est donc prouvé par la loi de Kepler & par celle de Neuton, que chaque Planete gravite vers le Soleil, ..." (Таким образом, закон Кеплера и закон Ньютона доказывают, что каждая планета вращается вокруг Солнца ...)

[4] С п. 162: "Par une des grandes loix de Kepler, toute Planete décrit des aires égales en temp égaux: par une autre loi non-moins sûre, chaque Planete fait sa révolution autour du Soleil en telle sort, que si, sa moyenne distance au Soleil est 10 . prenez le cube de ce nombre, ce qui sera 1000., & le tems de la révolution de cette Planete autour du Soleil sera пропорционально à la racine qurée de ce nombre 1000 ". (Согласно одному из великих законов Кеплера каждая планета описывает равные площади в равное время; согласно другому, не менее определенному закону, каждая планета совершает свой оборот вокруг Солнца таким образом, что если ее среднее расстояние от Солнца равно 10, куб этого числа, которое будет равно 1000, и время обращения этой планеты вокруг Солнца будет пропорционально квадратному корню из этого числа 1000.)

[5] С п. 205: "Il est donc prouvé par la loi de Kepler & par celle de Neuton, que chaque Planete gravite vers le Soleil, ..." (Таким образом, закон Кеплера и закон Ньютона доказывают, что каждая планета вращается вокруг Солнца ...)

[Wilson_1994-2] а ^б Уилсон, Кертис (май 1994 г.). "Законы Кеплера, так называемые" (PDF). HAD Новости (31): 1–2. Получено 27 декабря, 2016.

[3] Де ла Ланде, Астрономия, т. 1 (Париж, Франция: Desaint & Saillant, 1764). См. Например:
Со страницы 390: "… Mais suivant la fameuse loi de Kepler, qui sera Expiquée dans le Livre suivant (892), le rapport des temps périodiques est toujours plus grand que celui des distance, une planete cinq fois plus éloignée du soleil, emploie à faire sa révolution fois plus de temps ou environmental;… " (… Но согласно известному закону Кеплера, который будет объяснен в следующей книге [т.е. главе] (параграф 892), отношение периодов всегда больше, чем отношение расстояний [так что, например,] планете, находящейся в пять раз дальше от Солнца, требуется примерно в двенадцать раз больше времени, чтобы совершить свой оборот [вокруг Солнца];…)
Со страницы 429: "Les Quarrés des Temps périodiques sont Com les Cubes des Distances. 892. La plus fameuse loi du mouvement des plantes découverte par Kepler, est celle du repport qu'il ya entre les grandeurs de leurs orbites, & le temps qu'elles emploient à les parcourir;… " (Квадраты периодов подобны кубам расстояний. 892. Самый известный закон движения планет, открытый Кеплером, - это соотношение между размерами их орбит и временами, которые [планеты] требуют, чтобы пройти их;…)
Со страницы 430: "Les Aires sont correnelles au Temps. 895. Cette loi générale du mouvement des planetes devenue si importante dans l'Astronomie, sçavior, que les aires sont correnelles au temps, est encore une des découvertes de Kepler; ..." (Площади пропорциональны времени. 895. Этот общий закон движения планет, [который] стал настолько важным в астрономии, а именно, что площади пропорциональны времени, является одним из открытий Кеплера; ...)
Со страницы 435: «В апелле cette loi des aires пропорциональные aux temps, Loi de Kepler, aussi bien que celle de l'article 892, du nome de ce célebre Inventeur;…» (Один назвал этот закон площади, пропорциональной времени (закон Кеплера), а также закон параграфа 892 по имени этого знаменитого изобретателя; ...)

[8] Со страницы 390: "… Mais suivant la fameuse loi de Kepler, qui sera Expiquée dans le Livre suivant (892), le rapport des temps périodiques est toujours plus grand que celui des distance, une planete cinq fois plus éloignée du soleil, emploie à faire sa révolution fois plus de temps ou environmental;… " (… Но согласно известному закону Кеплера, который будет объяснен в следующей книге [т.е. главе] (параграф 892), отношение периодов всегда больше, чем отношение расстояний [так что, например,] планете, находящейся в пять раз дальше от Солнца, требуется примерно в двенадцать раз больше времени, чтобы совершить свой оборот [вокруг Солнца];…)

[9] Со страницы 429: "Les Quarrés des Temps périodiques sont Com les Cubes des Distances. 892. La plus fameuse loi du mouvement des plantes découverte par Kepler, est celle du repport qu'il ya entre les grandeurs de leurs orbites, & le temps qu'elles emploient à les parcourir;… " (Квадраты периодов подобны кубам расстояний. 892. Самый известный закон движения планет, открытый Кеплером, - это соотношение между размерами их орбит и временами, которые [планеты] требуют, чтобы пройти их;…)

[10] Со страницы 430: "Les Aires sont correnelles au Temps. 895. Cette loi générale du mouvement des planetes devenue si importante dans l'Astronomie, sçavior, que les aires sont correnelles au temps, est encore une des découvertes de Kepler; ..." (Площади пропорциональны времени. 895. Этот общий закон движения планет, [который] стал настолько важным в астрономии, а именно, что площади пропорциональны времени, является одним из открытий Кеплера; ...)

[11] Со страницы 435: «В апелле cette loi des aires пропорциональные aux temps, Loi de Kepler, aussi bien que celle de l'article 892, du nome de ce célebre Inventeur;…» (Один назвал этот закон площади, пропорциональной времени (закон Кеплера), а также закон параграфа 892 по имени этого знаменитого изобретателя; ...)

[4] Роберт Смолл, Отчет об астрономических открытиях Кеплера (Лондон, Англия: Дж. Моуман, 1804 г.), С. 298–299.

[5] Роберт Смолл, Отчет об астрономических открытиях Кеплера (Лондон, Англия: Дж. Моуман, 1804 г.).

[Stephenson1994-6] Брюс Стивенсон (1994). Физическая астрономия Кеплера. Издательство Принстонского университета. п. 170. ISBN 978-0-691-03652-6.

[7] Astronomia nova Aitiologitis, seu Physica Coelestis tradita Commentariis de Motibus stellae Martis ex monitoringibus G.V. Tychnonis.Prague 1609; Англ. тр. W.H. Донахью, Кембридж, 1992.

[8] В его Astronomia nova, Кеплер представил лишь доказательство того, что орбита Марса эллиптическая. Доказательства того, что орбиты других известных планет имеют эллиптическую форму, были представлены только в 1621 году.
См .: Иоганн Кеплер, Astronomia nova … (1609), п. 285. Отказавшись от круговой и овальной орбит, Кеплер пришел к выводу, что орбита Марса должна быть эллиптической. Сверху страницы 285: "Ergo ellipsis est Planetæ iter;…" (Таким образом, эллипс - это путь планеты [т.е. Марса];…) Далее на той же странице: «… Ut sequence capite patescet: ubi simul etiam manifestrabitur, nullam Planetæ relinqui figuram Orbitæ, præterquam perfecte ellipticam;…» (... как будет показано в следующей главе: где также будет доказано, что необходимо отказаться от любой фигуры на орбите планеты, кроме идеального эллипса; ...) А затем: «Caput LIX. Demonstratio, quod orbita Martis,…, fiat perfecta ellipsis:…» (Глава 59. Доказательство того, что орбита Марса,…, является совершенным эллипсом:…) Геометрическое доказательство того, что орбита Марса является эллипсом, появляется как Protheorema XI на страницах 289–290.
Кеплер заявил, что каждая планета движется по эллиптическим орбитам, имея Солнце в одном фокусе: Иоганн Кеплер, Epitome Astronomiae Copernicanae [Краткое изложение астрономии Коперника] (Линц («Lentiis ad Danubium»), (Австрия): Иоганн Планк, 1622), книга 5, часть 1, III. De Figura Orbitura (III. На рисунке [т.е. форме] орбит), страницы 658–665. С п. 658: "Ellipsin fieri orbitam planetæ…" (Из эллипса образуется орбита планеты…). С п. 659: «… Подошва (Foco altero huius ellipsis)…» (… Солнце (другой фокус этого эллипса)…).

[Holton-9] а ^б Холтон, Джеральд Джеймс; Кисть, Стивен Г. (2001). Физика, человеческое приключение: от Коперника до Эйнштейна и не только (3-е изд. В мягкой обложке). Пискатауэй, Нью-Джерси: Издательство Университета Рутгерса. С. 40–41. ISBN 978-0-8135-2908-0. Получено 27 декабря, 2009.

[10] В его Astronomia nova ... (1609 г.) Кеплер не представил свой второй закон в его современной форме. Он сделал это только в своем Воплощение 1621 г. Более того, в 1609 г. он представил свой второй закон в двух различных формах, которые ученые называют «законом расстояния» и «законом площади».
Его «закон расстояния» представлен в: "Caput XXXII. Virtutem quam Planetam movet in correcum attuari cum discessu a fonte." (Глава 32. Сила, перемещающая планету по кругу, ослабевает по мере удаления от источника.) См .: Иоганн Кеплер, Astronomia nova … (1609), С. 165–167. На странице 167, Кеплер утверждает: «…, Quanto longior est αδ quam αε, tanto diutius moratur Planeta in certo aliquo arcui excentrici apud δ, quam in quali arcu excentrici apud ε». (…, Поскольку αδ длиннее αε, планета будет оставаться на определенной дуге эксцентрика вблизи δ, чем на такой же дуге эксцентрика около ε.) То есть, чем дальше планета находится от Солнца ( в точке α), тем медленнее он движется по своей орбите, поэтому радиус от Солнца до планеты проходит через равные области за равное время. Однако, как представил Кеплер, его аргумент верен только для кругов, а не для эллипсов.
Его «региональный закон» представлен в: «Caput LIX. Demonstratio, quod orbita Martis,…, fiat perfecta ellipsis:…» (Глава 59. Доказательство того, что орбита Марса,… является идеальным эллипсом:…), Protheorema XIV и XV, С. 291–295. На верхней стр. 294, он гласит: "Arcum ellipseos, cujus moras metitur area AKN, debere terminari в LK, ut sit AM". (Дуга эллипса, продолжительность которой ограничена [т. Е. Измеряется] площадью AKM, должна заканчиваться в LK, так, чтобы она [т. Е. Дуга] была AM.) Другими словами, время, которое Марс требуется, чтобы двигаться по дуге AM его эллиптической орбиты, измеряется площадью сегмента AMN эллипса (где N - положение Солнца), которая, в свою очередь, пропорциональна сечению AKN круга, окружающего эллипс. и это касается его. Следовательно, область, которая сметается по радиусу от Солнца до Марса, когда Марс движется по дуге своей эллиптической орбиты, пропорциональна времени, которое Марсу требуется для движения по этой дуге. Таким образом, радиус от Солнца до Марса охватывает равные площади в равные времена.
В 1621 году Кеплер вновь сформулировал свой второй закон для любой планеты: Иоганн Кеплер, Epitome Astronomiae Copernicanae [Краткое изложение астрономии Коперника] (Линц ("Lentiis ad Danubium"), (Австрия): Иоганн Планк, 1622), книга 5, стр. 668. Со страницы 668: «Dictum quidem est in superioribus, divisa orbita in parriculas minutissimas æquales: accrescete iis moras planetæ per eas, в пропорции intervallorum inter eas & Solem». (Выше было сказано, что если орбита планеты разделена на наименьшие равные части, времена планеты в них увеличиваются в соотношении расстояний между ними и солнцем.) То есть скорость планеты вдоль его орбита обратно пропорциональна расстоянию от Солнца. (Оставшаяся часть абзаца ясно показывает, что Кеплер имел в виду то, что теперь называется угловой скоростью.)

[19] Его «закон расстояния» представлен в: "Caput XXXII. Virtutem quam Planetam movet in correcum attuari cum discessu a fonte." (Глава 32. Сила, перемещающая планету по кругу, ослабевает по мере удаления от источника.) См .: Иоганн Кеплер, Astronomia nova … (1609), С. 165–167. На странице 167, Кеплер утверждает: «…, Quanto longior est αδ quam αε, tanto diutius moratur Planeta in certo aliquo arcui excentrici apud δ, quam in quali arcu excentrici apud ε». (…, Поскольку αδ длиннее αε, планета будет оставаться на определенной дуге эксцентрика вблизи δ, чем на такой же дуге эксцентрика около ε.) То есть, чем дальше планета находится от Солнца ( в точке α), тем медленнее он движется по своей орбите, поэтому радиус от Солнца до планеты проходит через равные области за равное время. Однако, как представил Кеплер, его аргумент верен только для кругов, а не для эллипсов.

[20] Его «региональный закон» представлен в: «Caput LIX. Demonstratio, quod orbita Martis,…, fiat perfecta ellipsis:…» (Глава 59. Доказательство того, что орбита Марса,… является идеальным эллипсом:…), Protheorema XIV и XV, С. 291–295. На верхней стр. 294, он гласит: "Arcum ellipseos, cujus moras metitur area AKN, debere terminari в LK, ut sit AM". (Дуга эллипса, продолжительность которой ограничена [т. Е. Измеряется] площадью AKM, должна заканчиваться в LK, так, чтобы она [т. Е. Дуга] была AM.) Другими словами, время, которое Марс требуется, чтобы двигаться по дуге AM его эллиптической орбиты, измеряется площадью сегмента AMN эллипса (где N - положение Солнца), которая, в свою очередь, пропорциональна сечению AKN круга, окружающего эллипс. и это касается его. Следовательно, область, которая сметается по радиусу от Солнца до Марса, когда Марс движется по дуге своей эллиптической орбиты, пропорциональна времени, которое Марсу требуется для движения по этой дуге. Таким образом, радиус от Солнца до Марса охватывает равные площади в равные времена.

[Kepler_1619-11] а ^б Иоганн Кеплер, Harmonices Mundi [Гармония мира] (Линц, (Австрия): Иоганн Планк, 1619), книга 5, глава 3, п. 189. Снизу п. 189: "Sed res est certissima precisionissimaque quod" proportio qua est inter binorum quorumcunque Planetarum tempora periodica, сидеть præcise sesquialtera ratiois mediarum distantiarum,… " (Но совершенно точно и точно, что Пропорция периодов времени любых двух планет - это в точности полуторная [то есть отношение 3: 2] их средних расстояний,… ")
Английский перевод Кеплера Harmonices Mundi доступно как: Иоганн Кеплер с Э. Дж. Айтоном, А. М. Дунканом и Дж. В. Филд, пер., Гармония мира (Филадельфия, Пенсильвания: Американское философское общество, 1997); особенно видеть п. 411.

[12] Национальная ассоциация учителей наук о Земле (9 октября 2008 г.). «Таблица данных для планет и карликовых планет». Окна во Вселенную. Получено 2 августа 2018.

[15] Уилбур Эпплбаум (2000). Энциклопедия научной революции: от Коперника до Ньютона. Рутледж. п. 603. Bibcode:2000esrc.book ..... A. ISBN 978-1-135-58255-5.

[16] Рой Портер (1992). Научная революция в национальном контексте. Издательство Кембриджского университета. п.102. ISBN 978-0-521-39699-8.

[17] Виктор Гийемен; Шломо Штернберг (2006). Вариации на тему Кеплера. American Mathematical Soc. п. 5. ISBN 978-0-8218-4184-6.

[Wolfram2nd-18] Брайант, Джефф; Павлик, Александр. "Второй закон Кеплера ", Вольфрам Демонстрационный проект. Проверено 27 декабря 2009 года.

[19] Бертт, Эдвин. Метафизические основы современной физической науки. п. 52.

[Holton3-20] Джеральд Джеймс Холтон, Стивен Г. Браш (2001). Физика, человеческое приключение. Издательство Университета Рутгерса. п. 45. ISBN 978-0-8135-2908-0.

[21] Каспар, Макс (1993). Кеплер. Нью-Йорк: Дувр.

[22] И. Ньютон, Principia, п. 408 в переводе И. Коэн и А. Уитмен

[23] И. Ньютон, Principia, п. 943 в переводе И. Коэн и А. Уитмен

[24] Шварц, Рене. «Меморандум № 1: элементы кеплеровской орбиты → декартовы векторы состояний» (PDF). Получено 4 мая 2018.

[25] Мюллер, М. (1995). «Уравнение времени - проблема астрономии». Acta Physica Polonica A. Получено 23 февраля 2013.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[Nb 1]

[Nb 2]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

Иоганн Кеплер
Научная карьера	Гипотеза Кеплера Законы движения планет Кеплера Орбита Кеплера Треугольник Кеплера Уравнение Кеплера Многогранники Кеплера Сверхновая Кеплера Кеплеровский телескоп
Работает	Mysterium Cosmographicum (1596) Де Стелла Нова (1606) Astronomia nova (1609) Epitome Astronomiae Copernicanae (1618, 1620-21) Harmonices Mundi (1619) Таблицы Рудольфина (1627) Сомниум (1634)
Связанный	Die Harmonie der Welt (опера) Катарина Кеплер (мать) Якоб Барч (зять) Кеплер (опера) Космический телескоп Кеплера Иоганн Кеплер Квадроцикл Список однофамильцев

Сэр Исаак Ньютон
Публикации	Флюсии (1671) Де Моту (1684) Principia (1687; письмо ) Opticks (1704) Запросы (1704) Арифметика (1707) De Analysi (1711)
Другие сочинения	Quaestiones (1661–1665) "стоя на плечах гигантов " (1675) Заметки о еврейском храме (ок. 1680 г.) "Общий Схолиум " (1713; "гипотезы не финго " ) Древние королевства с поправками (1728) Искажения Священного Писания (1754)
Взносы	Исчисление текучесть Глубина удара Инерция Диск Ньютона Многоугольник Ньютона Тело Ньютона – Окунькова Отражатель Ньютона Ньютоновский телескоп Шкала Ньютона Металл Ньютона Колыбель Ньютона Спектр Структурная окраска
Ньютонианство	Аргумент ведра Неравенства Ньютона Закон охлаждения Ньютона Закон всемирного тяготения Ньютона постньютоновское расширение параметризованный гравитационная постоянная Теория Ньютона – Картана Уравнение Шредингера – Ньютона. Законы движения Ньютона Законы Кеплера Ньютоновская динамика Метод Ньютона в оптимизации Проблема Аполлония усеченный метод Ньютона Алгоритм Гаусса – Ньютона Кольца Ньютона Теорема Ньютона об овалах Проблема Ньютона – Пеписа Ньютоновский потенциал Ньютоновская жидкость Классическая механика Корпускулярная теория света Споры об исчислении Лейбница – Ньютона Обозначение Ньютона Вращающиеся сферы Пушечное ядро Ньютона Формулы Ньютона – Котеса Метод Ньютона обобщенный метод Гаусса – Ньютона Фрактал Ньютона Личности Ньютона Полином Ньютона Теорема Ньютона о вращающихся орбитах Уравнения Ньютона – Эйлера Число Ньютона проблема с числом поцелуев Фактор Ньютона Параллелограмм силы Теорема Ньютона – Пюизо Абсолютное пространство и время Светоносный эфир Ньютоновский ряд стол
Личная жизнь	Усадьба Вулсторпов (место рождения) Cranbury Park (дома) Ранние годы Более поздняя жизнь Религиозные взгляды Оккультные исследования Научная революция Коперниканская революция
связи	Кэтрин Бартон (племянница) Джон Кондуитт (племянник в законе) Исаак Барроу (профессор) Уильям Кларк (наставник) Бенджамин Пуллейн (репетитор) Джон Кейл (ученик) Уильям Стьукли (друг) Уильям Джонс (друг) Авраам де Муавр (друг)
Изображения	Ньютон Блейк (монотипия) Ньютон Паолоцци (скульптура)
Тезка	Институт Исаака Ньютона Медаль Исаака Ньютона Телескоп Исаака Ньютона Исаак Ньютон Группа телескопов Ньютон (единица)
Категории	► Исаак Ньютон