Помощь гравитации - Gravity assist

Анимация Вояджер 1с траектория с 5 сентября 1977 г. по 30 декабря 1981 г.
  Вояджер 1 ·   Земля ·   Юпитер ·   Сатурн ·   солнце

Анимация Вояджер 2с траектория с 20 августа 1977 г. по 30 декабря 2000 г.
  Вояджер 2 ·   Земля ·   Юпитер ·   Сатурн ·   Уран ·   Нептун ·   солнце

Часть серии по
Астродинамика
Орбитальная механика
Параметры орбиты Апсис Аргумент периапсиса Азимут Эксцентриситет Наклон Средняя аномалия Орбитальные узлы Большая полуось Истинная аномалия
Типы двухчастичные орбиты, от эксцентриситет Круговая орбита Эллиптическая орбита Переходная орбита (Переходная орбита Хомана Биэллиптическая переходная орбита ) Параболическая орбита Гиперболическая орбита Радиальная орбита Затухающая орбита
Уравнения Динамическое трение Скорость убегания Уравнение Кеплера Законы движения планет Кеплера Орбитальный период Орбитальная скорость Поверхностная гравитация Удельная орбитальная энергия Уравнение Vis-viva
Небесная механика
Гравитационные воздействия Барицентр Сфера холма Возмущения Сфера влияния
N-тела орбиты Лагранжевые точки (Гало-орбиты ) Орбиты Лиссажу Ляпуновские орбиты
Инженерия и эффективность
Предполетная инженерия Соотношение масс Доля полезной нагрузки Массовая доля топлива Уравнение ракеты Циолковского
Меры эффективности Помощь гравитации Эффект Оберта

В орбитальная механика и аэрокосмическая техника, а гравитационная рогатка, гравитационный маневр, или свинг это использование относительного движения (например, орбита вокруг солнце ) и сила тяжести из планета или другой астрономический объект изменить дорожка и скорость из космический корабль, как правило, чтобы сэкономить пропеллент и снизить расходы.

Помощь гравитации может быть использована для ускоряться космический корабль, то есть, чтобы увеличить или уменьшить его скорость или изменить его путь. «Помощь» обеспечивается движением гравитирующего тела, когда оно тянет за собой космический корабль.^[1] Гравитационный маневр впервые был использован в 1959 году, когда советский зонд Луна 3 сфотографировал обратную сторону Луны и использовался межпланетными зондами из Маринер 10 и далее, включая два Вояджер примечательные облет Юпитера и Сатурна.

Объяснение

Пример встречи.^[2]
В системе координат планеты космический зонд улетает с той же скоростью, с которой прибыл. Но при наблюдении в системе отсчета Солнечной системы (привязанной к Солнцу) польза от этого маневра становится очевидной. Здесь можно увидеть, как зонд набирает скорость, используя энергию скорости планеты, вращающейся вокруг Солнца. (Если траектория предназначена для прохождения перед планетой, а не позади нее, гравитационный ассистент можно использовать в качестве маневра торможения, а не ускорения.) Поскольку масса зонда на много порядков меньше, чем у планеты , в то время как результат на зонде весьма значительный, реакция замедления, которую испытывает планета, согласно Третий закон Ньютона, совершенно незаметно.

Возможные результаты гравитационного маневра в зависимости от вектора скорости и положения пролета приближающегося космического корабля

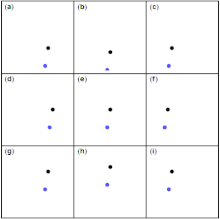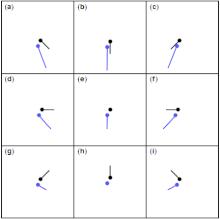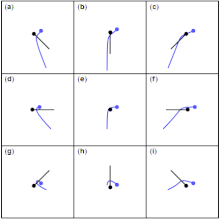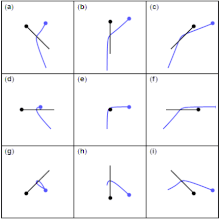
Гравитационная помощь вокруг планеты изменяет космический корабль скорость (относительно солнце ) входя и выходя из гравитационной сферы влияния планеты. Скорость космического корабля увеличивается по мере приближения к планете и уменьшается при выходе из-под его гравитационного притяжения (что примерно такое же), но поскольку планета вращается вокруг Солнца, космический корабль влияет на это движение во время маневра. Чтобы увеличить скорость, космический корабль летит вместе с движением планеты, приобретая при этом часть орбитальной энергии планеты; чтобы уменьшить скорость, космический корабль летит против движения планеты, чтобы передать планете часть своей орбитальной энергии - в обоих типах маневра передача энергии по сравнению с общей орбитальной энергией планеты незначительна. Сумма кинетических энергий обоих тел остается постоянной (см. упругое столкновение ). Таким образом, маневр рогатки может быть использован для изменения траектории и скорости космического корабля относительно Солнца.

Близкую аналогию с землей дает теннисный мяч, отскакивающий от движущегося поезда. Представьте, что вы стоите на платформе поезда и бросаете мяч на скорости 30 км / ч в поезд, приближающийся со скоростью 50 км / ч. Машинист поезда видит, как мяч приближается со скоростью 80 км / ч, а затем удаляется со скоростью 80 км / ч после того, как мяч упруго отскакивает от передней части поезда. Однако из-за движения поезда скорость отправления составляет 130 км / ч по отношению к платформе поезда; мяч добавил вдвое большую скорость поезда к своей собственной.

Перевод этой аналогии в космос: на планете система отсчета, космический корабль имеет вертикальную скорость v относительно планеты. После срабатывания рогатки космический корабль покидает курс на 90 градусов к тому, по которому он прибыл. Он по-прежнему будет иметь скорость v, но в горизонтальном направлении.^[2] В системе отсчета Солнца планета имеет горизонтальную скорость v, и, используя теорему Пифагора, космический корабль первоначально имеет общую скорость √2v. После того, как космический корабль покинет планету, он будет иметь скорость v + v = 2v, набирая около 0,6v.^[2]

Этот упрощенный пример невозможно уточнить без дополнительных деталей относительно орбиты, но если космический корабль движется по траектории, которая образует гипербола, он может покинуть планету в обратном направлении, не запуская двигатель. Этот пример также является одной из многих траекторий и наборов скорости, которые может иметь космический корабль.

Это объяснение может показаться нарушающим закон сохранения энергии и импульса, очевидно, из ничего прибавляя скорости космическому кораблю, но влияние космического корабля на планету также необходимо учитывать, чтобы получить полную картину задействованной механики. Линейный импульс, полученный космическим кораблем, равен по величине импульсу, потерянному планетой, поэтому космический корабль набирает скорость, а планета теряет скорость. Однако огромная масса планеты по сравнению с космическим кораблем делает результирующее изменение ее скорости пренебрежимо малым даже по сравнению с космическим кораблем. орбитальные возмущения планеты претерпевают из-за взаимодействия с другими небесными телами в астрономически короткие сроки. Например, один метрическая тонна - типичная масса для межпланетного космического зонда, тогда как Юпитер имеет массу почти 2 х 10²⁴ метрических тонн. Следовательно, космический корабль весом в одну тонну, пролетающий мимо Юпитера, теоретически приведет к потере планетой примерно 5 x 10⁻²⁵ км / с орбитальной скорости на каждый км / с скорости относительно Солнца, набранной космическим кораблем. Для всех практических целей, поскольку влияние на планету настолько незначительно (поскольку планеты намного массивнее космических кораблей), их можно не учитывать при расчетах.^[3]

Реалистичные изображения встреч в космосе требуют рассмотрения трех измерений. Применяются те же принципы, только добавление скорости планеты к скорости космического корабля требует векторное сложение, как показано ниже.

Двумерная схема гравитационной рогатки. Стрелки показывают направление, в котором движется космический корабль до и после столкновения. Длина стрелок показывает скорость космического корабля.

Воспроизвести медиа

Мессенджер использует Землю в качестве гравитационной рогатки для замедления и выхода на орбиту вокруг Меркурия.

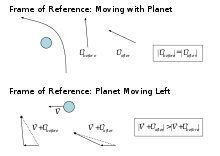
Из-за обратимость орбит, гравитационные рогатки также могут использоваться для снижения скорости космического корабля. И то и другое Маринер 10 и МЕССЕНДЖЕР выполнил этот маневр, чтобы достичь Меркурий.

Если требуется даже большая скорость, чем можно получить только от гравитации, самый экономичный способ использовать ракетный ожог - сделать это рядом с перицентр (ближайший подход). Горение ракеты всегда дает одно и то же изменение скорости (Δv ), но изменение кинетической энергии пропорционально скорости транспортного средства во время ожога. Таким образом, чтобы получить максимальную кинетическую энергию от ожога, ожог должен происходить с максимальной скоростью транспортного средства в перицентре. Эффект Оберта описывает эту технику более подробно.

Вывод

Формулы для гравитационного ассистента могут быть получены из знакомых формул для упругое столкновение. И импульс, и кинетическая энергия сохраняются, поэтому для тел с массами ${ displaystyle m_ {1}}$ и ${ displaystyle m_ {2}}$, и скорости ${ displaystyle u_ {1}}$ и ${ displaystyle u_ {2}}$ перед столкновением, и ${ displaystyle v_ {1}}$ и ${ displaystyle v_ {2}}$ после столкновения. В импульс до и после столкновения выражается:^[4]

${ displaystyle , ! m_ {1} u_ {1} + m_ {2} u_ {2} = m_ {1} v_ {1} + m_ {2} v_ {2}.}$

В кинетическая энергия выражается:^[4]

${ displaystyle { tfrac {1} {2}} m_ {1} u_ {1} ^ {2} + { tfrac {1} {2}} m_ {2} u_ {2} ^ {2} = { tfrac {1} {2}} m_ {1} v_ {1} ^ {2} + { tfrac {1} {2}} m_ {2} v_ {2} ^ {2}.}$

Эти уравнения можно решить, чтобы найти ${ displaystyle v_ {1}, v_ {2}}$ когда ${ displaystyle u_ {1}, u_ {2}}$ известны:^[5]

${ displaystyle { begin {array} {ccc} v_ {1} & = & displaystyle { frac {m_ {1} -m_ {2}} {m_ {1} + m_ {2}}} u_ {1 } + { frac {2m_ {2}} {m_ {1} + m_ {2}}} u_ {2} v_ {2} & = & displaystyle { frac {2m_ {1}} {m_ { 1} + m_ {2}}} u_ {1} + { frac {m_ {2} -m_ {1}} {m_ {1} + m_ {2}}} u_ {2} end {array}} }$

В случае пролета космического корабля над планетой масса космического корабля (${ displaystyle m_ {1}}$) ничтожно мала по сравнению с планетой (${ displaystyle m_ {2}}$) (${ displaystyle m_ {1} ll m_ {2}}$), так что это сводится к:

${ displaystyle { begin {array} {ccc} v_ {1} & приблизительно & -u_ {1} + 2u_ {2} v_ {2} & приблизительно & u_ {2} end {array}}}$

Историческое происхождение

В своей статье "Тем кто будет читать, чтобы строить" (Тем, кто будет читать [эту статью], чтобы построить [межпланетную ракету]),^[6] опубликовано в 1938 г., но датировано 1918–1919 гг.,^[7] Юрий Кондратюк предположил, что космический корабль, путешествующий между двумя планетами, может быть ускорен в начале и в конце своей траектории, используя силу притяжения лун двух планет. Эта часть его рукописи с учетом гравитационных ассистов не получила дальнейшего развития и не была опубликована до 1960-х годов.^[8] В своей статье 1925 г. "Проблема полета при помощи реактивных аппаратов: межпланетные полеты" [Проблемы полета на реактивном двигателе: межпланетные полеты],^[9] Фридрих Цандер показал глубокое понимание физики, лежащей в основе концепции гравитации и ее потенциала для межпланетных исследований Солнечной системы. Это еще более примечательно, если учесть, что другие великие астродинамики того времени никогда не рассматривали помощь гравитации, например Гвидо фон Пирке и Вальтер Хоманн.^[10]

Первым, кто рассчитал межпланетное путешествие с учетом нескольких гравитационных сил, был итальянский инженер. Гаэтано Крокко.^[11]

Гравитационный маневр впервые был использован в 1959 году, когда советский зонд Луна 3 сфотографировал обратную сторону Луны. Маневр опирался на исследования, проведенные под руководством Мстислав Келдыш на Математический институт им. В.А. Стеклова^[12] в том числе Всеволод Александрович Егоров.^[13][14]

Цель

График зависимости гелиоцентрической скорости "Вояджера-2" от расстояния до Солнца, иллюстрирующий использование силы тяжести для ускорения космического корабля по Юпитеру, Сатурну и Урану. Наблюдать Тритон "Вояджер-2" пролетел над северным полюсом Нептуна, что привело к ускорению вне плоскости эклиптики и уменьшению скорости вдали от Солнца.^[1]

Космический корабль, путешествующий с Земли на внутреннюю планету, увеличит свою относительную скорость, потому что он падает к Солнцу, а космический корабль, путешествующий с Земли на внешнюю планету, уменьшит свою скорость, поскольку он покидает окрестности Солнца.

Хотя орбитальная скорость внутренней планеты больше, чем у Земли, космический корабль, летящий на внутреннюю планету, даже с минимальной скоростью, необходимой для ее достижения, по-прежнему ускоряется гравитацией Солнца до скорости, заметно превышающей орбитальную скорость. этой целевой планеты. Если целью космического корабля является только полет над внутренней планетой, то обычно нет необходимости замедлять космический корабль. Однако, если космический корабль будет вставлен в орбита насчет этой внутренней планеты, значит, должен быть какой-то способ ее замедлить.

Точно так же, хотя орбитальная скорость внешней планеты меньше, чем у Земли, космический корабль, покидающий Землю с минимальной скоростью, необходимой для путешествия к какой-либо внешней планете, замедляется гравитацией Солнца до скорости, намного меньшей, чем орбитальная скорость та внешняя планета. Следовательно, должен быть какой-то способ ускорить космический корабль, когда он достигнет этой внешней планеты, если он собирается выйти на орбиту вокруг нее. Однако, если космический корабль будет ускорен до уровня, превышающего требуемый минимум, для выхода на орбиту вокруг целевой планеты потребуется меньшее количество топлива.^{[требуется разъяснение ][сомнительный – обсудить]} Кроме того, ускорение космического корабля в начале полета сокращает время полета.

Ракетные двигатели безусловно, может быть использован для увеличения и уменьшения скорости космического корабля. Однако для тяги ракеты необходимо топливо, топливо имеет массу и даже небольшое изменение скорости (известное как Δv, или "дельта-v", символ дельты используется для обозначения изменения, а "v" означает скорость ) означает гораздо большую потребность в топливе, необходимом для выхода из Земли гравитационный колодец. Это связано с тем, что двигатели первичной ступени не только должны поднимать дополнительное топливо, они также должны поднимать дополнительное топливо сверх того, которое необходимо для подъема. это дополнительное топливо. Требуемая взлетная масса увеличивается экспоненциально при увеличении требуемой дельта-v космического корабля.

Поскольку для доставки топлива в космос необходимо дополнительное топливо, космические миссии рассчитаны на ограниченный «бюджет» на топливо, известный как «бюджет delta-v ". Бюджет дельта-v - это, по сути, общее количество топлива, которое будет доступно после отрыва от земли, для ускорения, замедления, стабилизации от внешнего удара (частицами или другими внешними эффектами) или изменения направления, если оно не может быть получено. больше топлива. Вся миссия должна быть спланирована с учетом этих возможностей. Следовательно, методы изменения скорости и направления, которые не требуют сжигания топлива, являются предпочтительными, поскольку они обеспечивают дополнительные возможности маневрирования и улучшение курса без расходования топлива из ограниченного количества, которое был доставлен в космос. Гравитационные маневры могут значительно изменить скорость космического корабля без расхода топлива и могут сэкономить значительное количество топлива, поэтому они являются очень распространенным методом экономии топлива.

Пределы

Траектории, которые позволили космическому кораблю-близнецу НАСА "Вояджер" совершить поездку по четырем планетам-гигантам и достичь скорости, чтобы покинуть Солнечную систему.

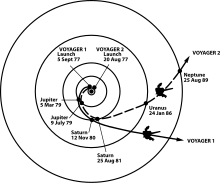
Основным практическим ограничением использования гравитационного маневра является то, что планеты и другие большие массы редко находятся в нужных местах, чтобы обеспечить путешествие к конкретному пункту назначения. Например, Вояджер миссии, начатые в конце 1970-х годов, стали возможны благодаря "большое путешествие «выравнивание Юпитера, Сатурна, Урана и Нептуна. Подобное выравнивание не произойдет снова до середины 22 века. Это крайний случай, но даже для менее амбициозных миссий бывают годы, когда планеты разбросаны по неподходящим частям. их орбиты.

Еще одно ограничение - это атмосфера доступной планеты, если таковая имеется. Чем ближе космический корабль может подойти, тем быстрее он перицентр скорость, поскольку сила тяжести ускоряет космический корабль, позволяя получить больше кинетической энергии от сгорания ракеты. Однако, если космический корабль окажется слишком глубоко в атмосфере, энергия, потерянная из-за сопротивления, может превысить получаемую за счет гравитации планеты. С другой стороны, атмосферу можно использовать для достижения аэротормоз. Также были теоретические предложения по использованию аэродинамический подъемник как космический корабль летит через атмосферу. Этот маневр, названный помощь при аэрогравитации, может изгибать траекторию на больший угол, чем одна только сила тяжести, и, следовательно, увеличивать выигрыш в энергии.

Даже в случае безвоздушного тела существует предел того, насколько близко может подойти космический корабль. Величина достижимого изменения скорости зависит от скорости приближения космического корабля и скорости убегания планеты в точке наибольшего сближения (ограниченной либо поверхностью, либо атмосферой).

Межпланетные рогатки с использованием самого Солнца невозможны, поскольку Солнце находится в состоянии покоя относительно Солнечной системы в целом. Тем не менее, укол, когда он находится рядом с Солнцем, имеет тот же эффект, что и мощная рогатка, описанная как Эффект Оберта. Это может значительно увеличить тягу космического корабля, но ограничено способностью космического корабля противостоять жаре.

Возможна межзвездная рогатка, использующая Солнце, например, включающая объект, прибывающий из другого места в нашей галактике и проносящийся мимо Солнца, чтобы ускорить его галактическое путешествие. Тогда энергия и угловой момент будут исходить от солнечной орбиты вокруг Млечный Путь. Эта концепция занимает видное место в Артур Кларк Роман 1972 года, отмеченный наградами Свидание с Рамой; его история касается межзвездного космического корабля, который использует Солнце для выполнения такого рода маневров и в процессе вызывает тревогу у многих нервных людей.

А вращающаяся черная дыра может оказать дополнительную помощь, если его ось вращения выровнена правильно. Общая теория относительности предсказывает, что большая вращающаяся масса производит перетаскивание кадра - вблизи объекта само пространство волочится в направлении вращения. Этот эффект производит любой обычный вращающийся объект. Хотя попытки измерить перемещение кадра вокруг Солнца не дали четких доказательств, эксперименты, проведенные Гравитационный зонд B обнаружили эффекты перетаскивания кадра, вызванные Землей.^[15] Общая теория относительности предсказывает, что вращающаяся черная дыра окружена областью пространства, называемой эргосфера, внутри которого стоять на месте (относительно вращения черной дыры) невозможно, потому что само пространство тащит со скоростью света в том же направлении, что и вращение черной дыры. В Процесс Пенроуза может предложить способ получения энергии из эргосферы, хотя для этого космическому кораблю потребуется сбросить некоторый «балласт» в черную дыру, и космическому кораблю пришлось бы расходовать энергию, чтобы доставить «балласт» к черной дыре.

Параметр Тиссерана и сила тяжести

Использование силы тяжести ограничено сохраняющейся величиной, называемой Параметр Тиссерана (или инвариант). Это приближение к Постоянная Якоби ограниченного проблема трех тел. Учитывая случай кометы, вращающейся вокруг Солнца, и последствия встречи с Юпитером, Феликс Тиссеран показало, что

${ displaystyle T_ {P} = { frac {a_ {J}} {a}} + 2 cdot { sqrt {{ frac {a} {a_ {J}}} (1-e ^ {2 })}} cos i}$

останется постоянным (где ${ Displaystyle а , !}$ комета большая полуось, ${ Displaystyle е , !}$ его эксцентриситет, ${ Displaystyle я , !}$ его склонность, и ${ displaystyle a_ {J}}$ Это большая полуось Юпитера). Это применимо, когда комета достаточно далеко от Юпитера, чтобы иметь четко определенные элементы орбиты, и до такой степени, что Юпитер намного менее массивен, чем Солнце, и находится на круговой орбите.

Эта величина сохраняется для любой системы из трех объектов, один из которых имеет незначительную массу, а другой - промежуточной массы и находится на круговой орбите. Примерами являются Солнце, Земля и космический корабль или Сатурн, Титан и космический корабль Кассини (с использованием большой полуоси возмущающего тела вместо ${ displaystyle a_ {J}}$). Это накладывает ограничение на то, как гравитационная помощь может использоваться для изменения орбиты космического корабля.

Параметр Тиссерана изменится, если космический корабль совершит движущий маневр или гравитационную поддержку какого-либо четвертого объекта, что является одной из причин того, что многие космические корабли часто сочетают в себе гравитацию Земли и Венеры (или Марса) или также выполняют большие маневры в глубоком космосе.

Хронология выдающихся примеров

Луна 3

Маневр гравитации впервые был использован в 1959 году, когда Луна 3 сфотографировал обратную сторону Луны.

Пионер 10

В декабре 1973 г. Пионер 10 космический корабль был первым, кто использовал эффект гравитационной рогатки для достижения космической скорости и покинул Солнечную систему.

Маринер 10

В Маринер 10 Зонд был первым космическим кораблем, который использовал эффект гравитационной рогатки для достижения другой планеты, пролетев мимо Венеры 5 февраля 1974 года и стал первым космическим кораблем, который исследовал Меркурий.

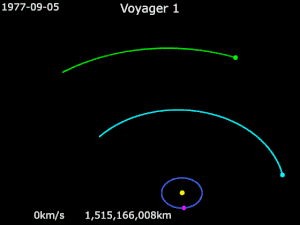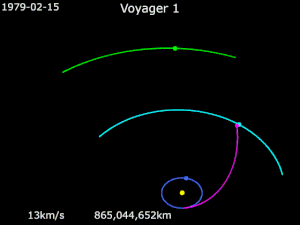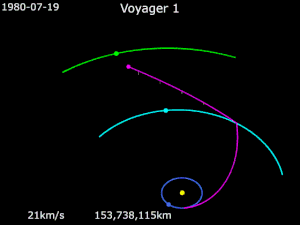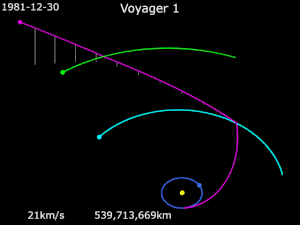
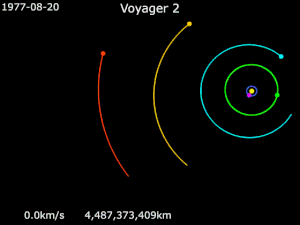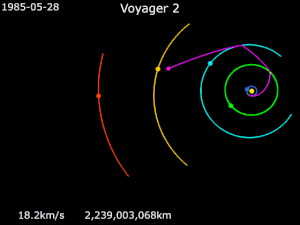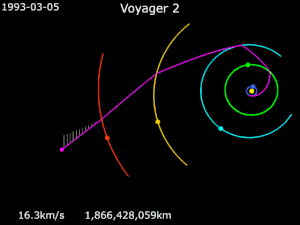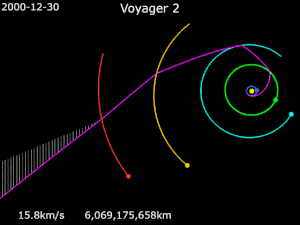
Вояджер 1

По состоянию на 21 июля 2018 г.^{[Обновить]}, Вояджер 1 больше 142,75Австралия (21,36 млрд км) от Солнца,^[16] и находится в межзвездное пространство.^[17] Он получил энергию, чтобы полностью избежать гравитации Солнца, совершая маневры с рогаткой вокруг Юпитера и Сатурна.^[18]

Галилео

Анимация Галилеос траектория с 19 октября 1989 г. по 30 сентября 2003 г.
  Галилео ·   Юпитер ·   Земля ·    Венера ·   951 Гаспра ·   243 Ида

В Галилео космический корабль был запущен НАСА в 1989 году на борту Космический шатл Атлантида. Его первоначальная миссия была рассчитана на использование прямого Трансфер Хоманна. Однако, Галилеос предполагаемый ускоритель, работающий на криогенном топливе Кентавр Ракета-носитель была запрещена в качестве "груза" Шаттла по соображениям безопасности после потери Космический шатл Претендент. С замененным на него разгонным блоком твердотопливной ракеты ВМС, который не мог обеспечить столько дельта-vГалилей не поднимался прямо к Юпитеру, а один раз пролетел мимо Венеры и дважды над Землей, чтобы достичь Юпитера в декабре 1995 года.

В Галилео инженерный обзор высказал предположение (но так и не смог окончательно доказать), что это более продолжительное время полета в сочетании с более сильным солнечным светом около Венеры привело к появлению смазки в Галилеос выход из строя основной антенны, что вынуждает использовать резервную антенну гораздо меньшего размера с последующим снижением скорости передачи данных с космического корабля.

Его последующий тур по Юпитерианские луны также использовали многочисленные маневры с рогаткой с этими лунами, чтобы сэкономить топливо и максимизировать количество встреч.

Улисс

Анимация Улисс' траектория с 6 октября 1990 г. по 29 июня 2009 г.
  Улисс ·   Земля ·   Юпитер ·   C / 2006 P1 ·   C / 1996 B2 ·   C / 1999 T1

В 1990 году НАСА запустило ЕКА космический корабль Улисс изучить полярный области Солнца. Все планеты вращаются примерно в плоскости, совпадающей с экватором Солнца. Таким образом, чтобы выйти на орбиту, проходящую над полюсами Солнца, космический корабль должен был бы устранить скорость 30 км / с, которую он унаследовал от орбиты Земли вокруг Солнца, и набрать скорость, необходимую для орбиты Солнца в направлении от полюса к Солнцу. полюсная плоскость, задачи, которые невозможно выполнить при текущем двигательная установка космического корабля только системы, что делает маневры помощи гравитационным необходимым.

Соответственно, Улисс сначала был отправлен к Юпитеру и был нацелен на то, чтобы достичь точки в космосе впереди и к югу от планеты. Проходя мимо Юпитера, зонд провалился сквозь гравитационное поле планеты, обменявшись импульсом с планетой. С помощью гравитационного маневра траектория зонда изогнулась на север относительно плоскости эклиптики на орбиту, которая проходит над полюсами Солнца. Используя этот маневр, Улисс требовалось ровно столько топлива, чтобы отправить его в точку рядом с Юпитером, что вполне соответствует текущим возможностям.

МЕССЕНДЖЕР

Анимация МЕССЕНДЖЕРс траектория с 3 августа 2004 г. по 31 марта 2011 г.
  МЕССЕНДЖЕР ·   Земля ·   Меркурий ·   Венера

В МЕССЕНДЖЕР миссия (запущенная в августе 2004 г.) широко использовала гравитационные вспомогательные средства, чтобы замедлить свою скорость перед обращением к Меркурию. Миссия MESSENGER включала один облет Земли, два облета Венеры и три облета Меркурия, прежде чем наконец прибыть к Меркурию в марте 2011 года со скоростью, достаточно низкой, чтобы обеспечить выход на орбиту с доступным топливом. Хотя облеты были в основном орбитальными маневрами, каждый из них давал возможность для важных научных наблюдений.

Кассини

В Кассини – Гюйгенс космический корабль дважды миновал Венеру, затем Землю и, наконец, Юпитер на пути к Сатурну. 6,7-летний транзит был немного дольше, чем шесть лет, необходимых для перехода Хомана, но уменьшил дополнительную скорость (дельта-v) требовалось около 2 км / с, так что большой и тяжелый Кассини зонд смог достичь Сатурна, что было бы невозможно при прямой передаче даже с Титан IV, самая большая ракета-носитель, доступная в то время. А Трансфер Хоманна до Сатурна потребуется в общей сложности 15,7 км / с дельта-v (без учета гравитационных колодцев Земли и Сатурна и без учета аэротормоз ), что выходит за рамки возможностей современных ракет-носителей и двигательных установок космических кораблей.

Кассини межпланетная траектория

Анимация Кассинис траектория с 15 октября 1997 г. по 4 мая 2008 г.
  Кассини – Гюйгенс ·   Юпитер ·   Сатурн ·   Земля ·   Венера ·   2685 Мазурский

Кассинис скорость относительно Солнца. Гравитация помогает формировать пики слева, а периодические изменения справа вызваны орбитой космического корабля вокруг Сатурна.

После выхода на орбиту вокруг Сатурна Кассини космический корабль использовал несколько Титан гравитация помогает ориентироваться в сложном орбитальном путешествии. Типичная встреча с Титаном изменила скорость космического корабля на 0,75 км / с, и космический корабль совершил 127 встреч с Титанами. Эти встречи позволили совершить орбитальный тур с широким диапазоном расстояний периапсиса и апоапсиса, различных ориентаций орбиты по отношению к Солнцу и наклонов орбиты от 0 ° до 74 °.

Розетта

Анимация Розеттас траектория с 2 марта 2004 г. по 9 сентября 2016 г.
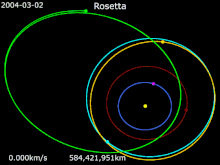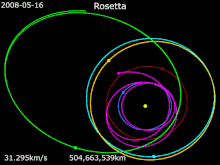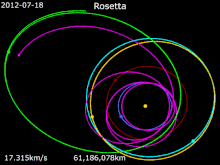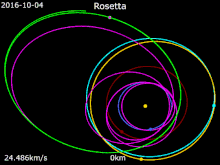
  Розетта ·   67P / C-G ·   Земля ·   Марс ·   21 Лютеция ·   2867 Штейнс

В Розетта Зонд, запущенный в марте 2004 года, использовал четыре гравитационных маневра (в том числе один всего в 250 км от поверхности Марса) для ускорения во внутренней части Солнечной системы. Это позволило ему соответствовать скорости 67P / Чурюмов – Герасименко комета в точке рандеву в августе 2014 года.

Юнона

В Космический корабль Юнона был запущен 5 августа 2011 г. (UTC). Траектория использовала ускорение скорости гравитации от Земля, совершенный облетом Земли в октябре 2013 года, через два года после его запуска 5 августа 2011 года.^[19] Таким образом Juno изменил свою орбиту (и скорость) к своей конечной цели, Юпитер всего через пять лет.

Анимация Юнонас траектория с 5 августа 2011 г. по 30 июля 2021 г.
  Юнона ·   Земля ·   Марс ·   Юпитер

Солнечный зонд Parker

НАСА Солнечный зонд Parker миссия, запущенная в 2018 году, будет использовать несколько гравитационных ассистентов на Венера убрать земные угловой момент с орбиты опуститься на расстояние 8,5 радиуса Солнца (5,9 Gm ) с Солнца. Миссия Parker Solar Probe будет самым близким приближением к Солнцу из любой космической миссии.

BepiColombo

Анимация BepiColomboс траектория с 20 октября 2018 г. по 2 ноября 2025 г.
  BepiColombo ·   Земля ·   Венера ·   Меркурий ·   солнце
Для более подробной анимации см. это видео.

BepiColombo это совместная миссия Европейское космическое агентство (ЕКА) и Японское агентство аэрокосмических исследований (JAXA) на планету Меркурий. Он был запущен 20 октября 2018 года. Он будет использовать технику гравитации с Земля однажды, с Венера дважды и шесть раз с Меркурий. BepiColombo назван в честь Джузеппе (Бепи) Коломбо кто был пионером в этом способе маневров.

Смотрите также

• 3753 Cruithne, астероид, который периодически сталкивается с Землей из гравитационной рогатки.
• Дельта-v бюджет
• Передача с низкой энергией, разновидность гравитационной помощи, при которой космический корабль гравитационно захватывает орбиту небесным телом. Этот метод обычно применяется в системе Земля-Луна.
• Динамическое трение
• Аномалия облета, аномальная дельта-v увеличение во время гравитации
• Гравитационная замочная скважина
• Межпланетная транспортная сеть
• ппроблема тела
• Новые горизонты, миссия с использованием гравитации (пролет мимо Юпитера), которая достигла Плутон 14 июля 2015 г.
• Пионер 10
• Пионер 11, миссия с помощью гравитации (пролет мимо Юпитера 1974-12-03) для достижения Сатурн в 1979 г.
• Пионер H, первая предложенная миссия за пределами эклиптики (OOE) для наблюдений за Юпитером и Солнцем
• СТЕРЕО, гравитационная миссия, в ходе которой с помощью Луны Земли два космических корабля были сброшены с орбиты Земли на гелиоцентрический орбита

использованная литература

внешние ссылки

• Основы космического полета: учебник по гравитации на NASA.gov
• Космические полеты и космические корабли: Gravity Assist, обсуждение на Phy6.org
• "Гравитационная рогатка". MathPages.com.
• Эксперимент с падением двойного шара
• «Рогатка с функцией гравитации. Предпосылки, принцип, приложения, части 1 и 2», на EEWorldoneline.com