Орбитальный маневр - Википедия - Orbital maneuver

В космический полет, орбитальный маневр (иначе известный как гореть) - это использование движущая сила системы для изменения орбита из космический корабль. Для космических аппаратов, далеких от Земли (например, находящихся на орбитах вокруг Солнца), орбитальный маневр называется маневр в дальнем космосе (DSM).^{[не проверено в теле ]}

Остальная часть полета, особенно в переводная орбита, называется каботажный.

Общий

Ракетное уравнение

Ракета массовые отношения от конечной скорости, рассчитанной по уравнению ракеты

В Уравнение ракеты Циолковского, или же уравнение идеальной ракеты это уравнение, которое полезно при рассмотрении транспортных средств, которые следуют основному принципу ракета: где устройство, которое может применять ускорение к самому себе (a толкать ), выбрасывая часть своей массы с большой скоростью и перемещаясь за счет сохранения импульс. В частности, это математическое уравнение, которое связывает дельта-v (максимальное изменение скорости ракеты, если не действуют другие внешние силы) с эффективная скорость истечения а начальная и конечная масса ракета (или другой двигатель реакции.)

Для любого такого маневра (или путешествия, включающего несколько таких маневров):

${ displaystyle Delta v = v _ { text {e}} ln { frac {m_ {0}} {m_ {1}}}}$

куда:

${ displaystyle m_ {0}}$ - начальная полная масса, включая топливо,

${ displaystyle m_ {1}}$ конечная общая масса,

${ displaystyle v _ { text {e}}}$ это эффективная скорость истечения (${ displaystyle v _ { text {e}} = I _ { text {sp}} cdot g_ {0}}$ куда ${ displaystyle I _ { text {sp}}}$ это удельный импульс выражается как период времени и ${ displaystyle g_ {0}}$ является стандартная сила тяжести ),

${ displaystyle Delta v }$ - дельта-v - максимальное изменение скорости транспортного средства (без воздействия внешних сил).

Дельта-v

Применяемое изменение скорости каждого маневра упоминается как дельта-v (${ Displaystyle Delta mathbf {v} ,}$).

Бюджет Delta-v

Общая дельта-v для всех и каждого маневра оценивается для миссии и называется бюджет delta-v. С хорошим приближением к бюджету delta-v разработчики могут оценить потребности космического корабля в топливе и полезной нагрузке, используя уравнение ракеты.

Импульсивные маневры

Рисунок 1: Аппроксимация маневра конечной тяги с импульсным изменением скорости

«Импульсивный маневр» - это математическая модель маневра как мгновенного изменения в космическом корабле. скорость (величина и / или направление), как показано на рисунке 1. Это предельный случай горения, чтобы генерировать определенное количество дельта-v, поскольку время горения стремится к нулю.

В физическом мире невозможно по-настоящему мгновенное изменение скорости, так как для этого потребуется «бесконечная сила», приложенная в течение «бесконечно короткого времени», но как математическая модель в большинстве случаев очень хорошо описывает эффект маневра на орбите.

Смещение вектора скорости после окончания реального горения от вектора скорости в то же время, возникающее в результате теоретического импульсного маневра, вызвано только разницей гравитационной силы вдоль двух путей (красный и черный на рисунке 1), которые в общем маленький.

На этапе планирования космических миссий разработчики сначала приблизят предполагаемые изменения орбиты, используя импульсные маневры, что значительно снижает сложность поиска правильных орбитальных переходов.

Применение низкой тяги в течение длительного периода времени

Применение малой тяги в течение более длительного периода времени называется неимпульсивный маневр (где «неимпульсивный» относится к маневру, который не является кратковременным, а не включает импульс - изменение импульса, которое явно должно иметь место).^{[нужна цитата ]}

Другой термин конечный ожог, где слово «конечный» используется для обозначения «ненулевого», или практически, опять же: за более длительный период.

Для нескольких космических миссий, таких как космическое рандеву, требуются высокоточные модели траекторий для достижения целей миссии. Расчет «конечного» ожога требует детальной модели космический корабль и его двигатели. К наиболее важным деталям относятся: масса, центр массы, момент инерции, положения подруливающих устройств, векторы тяги, кривые тяги, удельный импульс, толкать центроид зачеты и расход топлива.

Помогает

Эффект Оберта

В космонавтика, то Эффект Оберта где использование ракетный двигатель при движении на высокой скорости генерирует гораздо больше полезной энергии, чем при движении на низкой скорости. Эффект Оберта возникает из-за того, что пропеллент имеет больше полезной энергии (из-за своей кинетической энергии сверх его химической потенциальной энергии), и оказывается, что транспортное средство может использовать эту кинетическую энергию для выработки большей механической энергии. Он назван в честь Герман Оберт, то Австро-венгерский -родившийся, Немецкий физик и основоположник современного ракетная техника, который, по-видимому, первым описал эффект.^[1]

Эффект Оберта используется в пролет с двигателем или же Маневр Оберта где приложение импульса, как правило, от использования ракетного двигателя, близко к гравитационному телу (где гравитационный потенциал низкая, а скорость высокая) может дать гораздо большее изменение кинетическая энергия и конечная скорость (т.е. выше удельная энергия ), чем тот же импульс, приложенный дальше от тела на той же начальной орбите.

Поскольку маневр Оберта происходит в очень ограниченное время (на малой высоте), для генерации сильного импульса двигателю обязательно необходимо достичь высокой тяги (импульс по определению - это время, умноженное на тягу). Таким образом, эффект Оберта гораздо менее полезен для двигателей малой тяги, таких как ионные двигатели.

Исторически сложилось так, что непонимание этого эффекта привело исследователей к выводу, что межпланетные путешествия потребуют совершенно непрактичного количества топлива, так как без него необходимо огромное количество энергии.^[1]

Гравитационная помощь

Траектории, которые позволили космическому кораблю-близнецу НАСА Вояджер совершить поездку по четырем газовым планетам-гигантам и достичь скорости, чтобы покинуть нашу солнечную систему

В орбитальная механика и аэрокосмическая техника, а гравитационная рогатка, гравитационный маневр, или же свинг это использование относительного движения и сила тяжести из планета или другое небесное тело, чтобы изменить дорожка и скорость из космический корабль, как правило, чтобы сэкономить пропеллент, время, и расход. Помощь гравитации может быть использована для ускоряться, замедлить и / или изменить траекторию космического корабля.

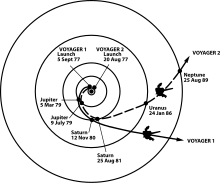
«Ассистент» обеспечивается движением (орбитальным угловой момент ) гравитирующего тела, когда оно тянет за собой космический корабль.^[2] Этот метод был впервые предложен в качестве маневра на полпути в 1961 году и использовался межпланетными зондами из Маринер 10 и далее, включая два Вояджер зонды заметных пролетов Юпитера и Сатурна.

Переходные орбиты

Выведение на орбиту - это общий термин для маневра, который представляет собой нечто большее, чем небольшая коррекция. Его можно использовать для маневра, чтобы изменить переводная орбита или орбита восхождения на стабильную, но также для изменения устойчивой орбиты на спуск: выведение на орбиту спуска. Также термин орбитальная инъекция используется, особенно для изменения стабильной орбиты на переходную, например транслунная инъекция (TLI), трансмарсианская инъекция (TMI) и закачка через Землю (TEI).

Передача Хоманна

Переходная орбита Хомана

В орбитальная механика, то Переходная орбита Хомана эллиптическая орбита, используемая для передачи между двумя круговые орбиты на разных высотах, на одной самолет.

Орбитальный маневр для выполнения перехода Хомана использует два импульса двигателя, которые перемещают космический корабль на переходную орбиту и с нее. Этот маневр был назван в честь Вальтер Хоманн, то Немецкий ученый, опубликовавший его описание в своей книге 1925 г. Die Erreichbarkeit der Himmelskörper (Доступность небесных тел).^[3] На Хоманна отчасти повлиял немецкий писатель-фантаст. Курд Ласвиц и его книга 1897 года Две планеты.^{[нужна цитата ]}

Биэллиптический перенос

Биэллиптический переход с синей на красную круговую орбиту

В космонавтика и аэрокосмическая техника, то двухэллиптический перенос орбитальный маневр, который перемещает космический корабль от одного орбита другому и может в определенных ситуациях потребовать меньше дельта-v чем Передача Хоманна маневр.

Биэллиптическая передача состоит из двух половин эллиптические орбиты. С начальной орбиты применяется дельта-v, переводящая космический аппарат на первую переходную орбиту с апоапсис в какой-то момент ${ displaystyle r_ {b}}$ подальше от центральный орган. В этот момент применяется вторая дельта-v, отправляющая космический аппарат на вторую эллиптическую орбиту с перицентр на радиусе конечной желаемой орбиты, где выполняется третья дельта-v, выводящая космический аппарат на желаемую орбиту.^{[нужна цитата ]}

Хотя для них требуется на один цикл двигателя больше, чем для передачи Хомана, и, как правило, требуется большее время в пути, для некоторых биэллиптических передач требуется меньшее общее значение дельта-v, чем для передачи Хомана, когда соотношение конечной и начальной большая полуось составляет 11,94 или больше, в зависимости от выбранной промежуточной большой полуоси.^[4]

Идея биэллиптической траектории переноса была впервые опубликована Ари Штернфельд в 1934 г.^[5]

Низкая передача энергии

А низкая передача энергии, или низкая энергия траектория, это маршрут в космосе, который позволяет космическому кораблю менять орбиты используя очень мало топлива.^[6][7] Эти маршруты работают в земной шар -Луна системе, а также в других системах, таких как перемещение между спутники Юпитера. Недостатком таких траекторий является то, что они требуют гораздо больше времени для завершения, чем передачи более высокой энергии (больше топлива), такие как Переходные орбиты Хомана.

Передача низкой энергии также известна как траектории границы слабой устойчивости или траектории баллистического захвата.

Передача низкой энергии происходит по особым путям в космосе, которые иногда называют Межпланетная транспортная сеть. Следование по этим путям позволяет преодолевать большие расстояния с небольшими затратами. дельта-v.

Изменение наклона орбиты

Изменение наклона орбиты орбитальный маневр, направленный на изменение склонность орбитального тела орбита. Этот маневр также известен как изменение плоскости орбиты, поскольку плоскость орбиты наклоняется. Этот маневр требует изменения вектора орбитальной скорости (дельта v ) на орбитальные узлы (то есть точка, где пересекаются начальная и желаемая орбиты, линия орбитальных узлов определяется пересечением двух орбитальных плоскостей).

В общем, изменение наклона может потребовать большого количества дельта-v для выполнения, и большинство специалистов по планированию миссий стараются избегать их, когда это возможно, для экономии топлива. Обычно это достигается запуском космического корабля непосредственно на желаемый наклон или как можно ближе к нему, чтобы минимизировать любое изменение угла наклона, необходимое в течение срока службы космического корабля.

Максимальная эффективность изменения наклона достигается при апоапсис, (или же апогей ), где орбитальная скорость ${ displaystyle v ,}$ самый низкий. В некоторых случаях может потребоваться меньшая общая дельта v, чтобы поднять спутник на более высокую орбиту, изменить плоскость орбиты на более высоком апогее, а затем опустить спутник до исходной высоты.^[8]

Траектория постоянной тяги

Постоянная тяга и постоянное ускорение траектории включают запуск двигателя космического корабля в продолжительном постоянном режиме работы. В предельном случае, когда ускорение транспортного средства велико по сравнению с местным ускорением свободного падения, космический корабль направлен прямо на цель (с учетом движения цели) и продолжает постоянно ускоряться при высокой тяге, пока не достигнет своей цели. В этом случае с большой тягой траектория приближается к прямой. Если требуется, чтобы космический корабль встретился с целью, а не выполнял облет, то космический корабль должен изменить свою ориентацию на полпути полета и замедлить оставшуюся часть пути.

На траектории постоянной тяги^[9] ускорение транспортного средства увеличивается в течение периода тяги, поскольку расход топлива означает, что масса транспортного средства уменьшается. Если вместо постоянной тяги автомобиль имеет постоянное ускорение, тяга двигателя должна уменьшаться во время движения по траектории.

Эта траектория требует, чтобы космический корабль сохранял высокое ускорение в течение длительного времени. Для межпланетных перелетов могут потребоваться дни, недели или месяцы постоянного рывка. В результате в настоящее время отсутствуют двигательные установки космических кораблей, способные использовать эту траекторию. Было высказано предположение, что некоторые формы ядерных (ядерных или термоядерных) ракет или ракет, работающих на антивеществе, будут способны двигаться по этой траектории.

Практически этот тип маневра используется в маневрах с малой тягой, например, с ионные двигатели, Двигатели на эффекте Холла, и другие. Эти типы двигателей имеют очень высокий удельный импульс (топливную экономичность), но в настоящее время доступны только с довольно низкой абсолютной тягой.

Свидание и стыковка

Фазировка орбиты

В астродинамика фазировка орбиты это корректировка временного положения космического корабля по его орбита, обычно описываемый как корректировка орбитального космического корабля истинная аномалия.

Космическое рандеву и стыковка

Gemini 7 сфотографировано с Gemini 6 в 1965 году.

А космическое рандеву орбитальный маневр, во время которого два космический корабль, одним из которых часто бывает космическая станция, прийти к тому же орбита и подходить на очень близкое расстояние (например, при визуальном контакте). Рандеву требует точного совпадения орбитальные скорости двух космических кораблей, позволяя им оставаться на постоянном расстоянии через орбитальная станция. Свидание может сопровождаться или не сопровождаться стыковка или швартовка, процедуры, которые приводят космический корабль в физический контакт и создают связь между ними.

Смотрите также

• Уравнения Клохесси-Уилтшира для анализа совместной орбиты
• Предотвращение столкновений (космический корабль)
• Облет (космический полет)
• Космические двигательные установки
• Орбитальный космический полет

Рекомендации

внешняя ссылка

• Справочник по автоматизированной сближению и стыковке космических аппаратов к Вигберт Фезе