Гиперболическая траектория - Hyperbolic trajectory

Синий путь на этом изображении - пример гиперболической траектории.

Гиперболическая траектория изображена в правом нижнем квадранте этой диаграммы, где гравитационная потенциальная яма центральной массы показывает потенциальную энергию, а кинетическая энергия гиперболической траектории показана красным. Высота кинетической энергии уменьшается по мере уменьшения скорости и увеличения расстояния согласно законам Кеплера. Та часть кинетической энергии, которая остается выше нуля полной энергии, связана с гиперболической избыточной скоростью.

Часть серии по
Астродинамика
Орбитальная механика
Параметры орбиты Апсис Аргумент периапсиса Азимут Эксцентриситет Наклон Средняя аномалия Орбитальные узлы Большая полуось Истинная аномалия
Виды двухчастичные орбиты, к эксцентриситет Круговая орбита Эллиптическая орбита Переходная орбита (Переходная орбита Хомана Биэллиптическая переходная орбита ) Параболическая орбита Гиперболическая орбита Радиальная орбита Затухающая орбита
Уравнения Динамическое трение Скорость убегания Уравнение Кеплера Законы движения планет Кеплера Орбитальный период Орбитальная скорость Поверхностная гравитация Удельная орбитальная энергия Уравнение Vis-viva
Небесная механика
Гравитационные воздействия Барицентр Сфера холма Возмущения Сфера влияния
N-тела орбиты Лагранжевые точки (Гало-орбиты ) Орбиты Лиссажу Ляпуновские орбиты
Инженерия и эффективность
Предполетная инженерия Соотношение масс Доля полезной нагрузки Массовая доля топлива Уравнение ракеты Циолковского
Меры эффективности Помощь гравитации Эффект Оберта

В астродинамика или же небесная механика, а гиперболическая траектория это траектория любого объекта вокруг центральный орган с более чем достаточной скоростью, чтобы избежать гравитационного воздействия центрального объекта. Название происходит от того, что согласно Ньютоновская теория такая орбита имеет форму гипербола. В более технических терминах это может быть выражено условием, что орбитальный эксцентриситет больше единицы.

Согласно упрощенным предположениям, тело, движущееся по этой траектории, будет двигаться к бесконечности, устанавливая конечную избыточную скорость относительно центрального тела. Аналогично параболические траектории, все гиперболические траектории также траектории ухода. В удельная энергия орбиты гиперболической траектории положительна.

Планетарные облеты, используемые для гравитационные рогатки, можно описать в пределах планеты сфера влияния с использованием гиперболических траекторий.

Параметры, описывающие гиперболическую траекторию

Подобно эллиптической орбите, гиперболическая траектория для данной системы может быть определена (без учета ориентации) ее большой полуосью и эксцентриситетом. Однако для гиперболической орбиты другие параметры могут быть более полезными для понимания движения тела. В следующей таблице перечислены основные параметры, описывающие путь тела, следующего по гиперболической траектории вокруг другого при стандартных предположениях, и формулы, связывающие их.

Эти уравнения могут быть неточными. Нужны дополнительные ссылки.

Уравнения гиперболической траектории

Элемент	Символ	Формула	с помощью ${ displaystyle v _ { infty}}$ (или же ${ displaystyle a}$), и ${ displaystyle b}$
Стандартный гравитационный параметр	${ displaystyle mu ,}$	${ displaystyle { frac {v ^ {2}} {(2 / r-1 / a)}}}$	${ displaystyle bv _ { infty} ^ {2} cot theta _ { infty}}$
Эксцентриситет (>1)	${ displaystyle e}$	${ displaystyle { frac { ell} {r_ {p}}} - 1}$	${ displaystyle { sqrt {1 + b ^ {2} / a ^ {2}}}}$
Большая полуось (<0)	${ Displaystyle а , !}$	${ Displaystyle 1 / (2 / р-v ^ {2} / му)}$	${ displaystyle - mu / v _ { infty} ^ {2}}$
Гиперболическая избыточная скорость	${ displaystyle v _ { infty}}$	${ displaystyle { sqrt {- mu / a}}}$
(Внешний) Угол между асимптотами	${ displaystyle 2 theta _ { infty}}$	${ Displaystyle 2 соз ^ {- 1} (- 1 / е)}$	${ Displaystyle пи +2 загар ^ {- 1} (б / а)}$[1]
Угол между асимптотами и сопряженной осью гиперболического пути подхода	${ displaystyle 2 nu}$	${ displaystyle 2 theta _ { infty} - pi}$	${ displaystyle 2 sin ^ {- 1} { bigg (} { frac {1} {(1 + r_ {p} * v _ { infty} ^ {2} / mu)}} { bigg) }}$
Параметр удара (малая полуось )	${ displaystyle b}$	${ displaystyle -a { sqrt {е ^ {2} -1}}}$
Полу-латусная прямая кишка	${ displaystyle ell}$	${ Displaystyle а (е ^ {2} -1)}$	${ displaystyle -b ^ {2} / a = h ^ {2} / mu}$
Расстояние периапсиса	${ displaystyle r_ {p}}$	${ Displaystyle а (1-е)}$	${ displaystyle { sqrt {a ^ {2} + b ^ {2}}} + a}$
Удельная орбитальная энергия	${ displaystyle varepsilon}$	${ displaystyle - mu / 2a}$	${ displaystyle v _ { infty} ^ {2} / 2}$
Удельный угловой момент	${ displaystyle h}$	${ displaystyle { sqrt { mu ell}}}$	${ displaystyle bv _ { infty}}$

Большая полуось, энергия и гиперболическая избыточная скорость

Большая полуось (${ Displaystyle а , !}$) не сразу виден с гиперболической траекторией, но может быть построен, поскольку это расстояние от перицентра до точки пересечения двух асимптот. Обычно, по соглашению, он отрицательный, чтобы различные уравнения согласовывались с эллиптическими орбитами.

Большая полуось напрямую связана с удельная орбитальная энергия (${ displaystyle epsilon ,}$) или же характерная энергия ${ displaystyle C_ {3}}$ орбиты и скорости, которой тело достигает при стремлении расстояния к бесконечности, гиперболическая избыточная скорость (${ Displaystyle v _ { infty} , !}$).

${ Displaystyle v _ { infty} ^ {2} = 2 epsilon = C_ {3} = - mu / a}$ или же ${ displaystyle a = - { mu / {v _ { infty} ^ {2}}}}$

куда: ${ displaystyle mu = Gm , !}$ это стандартный гравитационный параметр и ${ displaystyle C_ {3}}$ характерная энергия, обычно используемая при планировании межпланетных миссий.

Обратите внимание, что полная энергия положительна в случае гиперболической траектории (тогда как она отрицательна для эллиптической орбиты).

Эксцентриситет и угол между заходом на посадку и вылетом

При гиперболической траектории орбитальный эксцентриситет (${ Displaystyle е ,}$) больше 1. Эксцентриситет напрямую связан с углом между асимптотами. С эксцентриситетом чуть больше 1 гипербола имеет острую форму буквы «v». В ${ displaystyle e = { sqrt {2}}}$ асимптоты расположены под прямым углом. С ${ displaystyle e> 2}$ асимптоты разнесены более чем на 120 °, а расстояние между ними больше, чем большая полуось. По мере дальнейшего увеличения эксцентриситета движение приближается к прямой.

Угол между направлением перицентра и асимптотой от центрального тела равен истинная аномалия поскольку расстояние стремится к бесконечности (${ displaystyle theta _ { infty} ,}$), так ${ Displaystyle 2 theta _ { infty} ,}$ - внешний угол между направлениями подхода и отъезда (между асимптотами). потом

${ Displaystyle тета {_ { infty}} = соз ^ {- 1} (- 1 / е) ,}$ или же ${ Displaystyle е = -1 / соз тета {_ { infty}} ,}$

Параметр удара и дальность максимального сближения

Гиперболические траектории, за которыми следуют объекты, приближающиеся к центральному объекту (маленькая точка) с одинаковой гиперболической избыточной скоростью (и большой полуосью (= 1)) и с одного направления, но с разными параметрами удара и эксцентриситетом. Желтая линия действительно проходит вокруг центральной точки, приближаясь к ней.

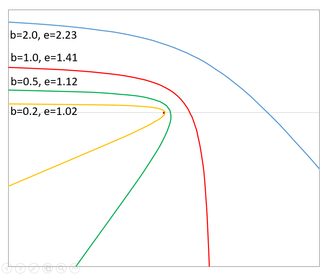
В прицельный параметр это расстояние, на которое тело, если бы оно продолжало двигаться невозмущенным путем, могло бы пропустить центральное тело на своем ближайший подход. Для тел, испытывающих гравитационные силы и следующих по гиперболическим траекториям, он равен малой полуоси гиперболы.

В ситуации, когда космический корабль или комета приближается к планете, прицельный параметр и избыточная скорость будут известны точно. Если центральное тело известно, то теперь можно определить траекторию, включая то, насколько близко приближающееся тело будет в перицентре. Если он меньше радиуса планеты, следует ожидать удара. Расстояние наибольшего сближения или перицентрическое расстояние определяется как:

${ displaystyle r_ {p} = - a (e-1) = mu / v {_ { infty}} ^ {2} ({ sqrt {1+ (bv {_ { infty}} ^ {2 } / mu) ^ {2}}} - 1)}$

Итак, если приближается комета земной шар (эффективный радиус ~ 6400 км) со скоростью 12,5 км / с (примерная минимальная скорость сближения тела, идущего с внешней стороны). Солнечная система ), чтобы избежать столкновения с Землей, параметр удара должен быть не менее 8600 км, или на 34% больше радиуса Земли. Тело приближается Юпитер (радиус 70000 км) от внешней части Солнечной системы со скоростью 5,5 км / ч, во избежание столкновения потребуется, чтобы параметр удара был не менее 770 000 км или в 11 раз больше радиуса Юпитера.

Если масса центрального тела неизвестна, его стандартный гравитационный параметр и, следовательно, его масса могут быть определены путем отклонения меньшего тела вместе с параметром удара и скоростью приближения. Поскольку обычно все эти переменные могут быть определены точно, пролет космического корабля даст хорошую оценку массы тела.

${ displaystyle mu = bv _ { infty} ^ {2} tan delta / 2}$ куда ${ displaystyle delta = 2 theta _ { infty} - pi}$ - угол, на который меньшее тело отклоняется от прямой на своем пути.

Уравнения движения

Позиция

В гиперболической траектории истинная аномалия ${ displaystyle theta}$ связана с расстоянием между вращающимися телами (${ Displaystyle г ,}$) посредством уравнение орбиты:

${ Displaystyle г = { гидроразрыва { ell} {1 + е cdot cos theta}}}$

Связь между истинной аномалией θ и эксцентрическая аномалия E (в качестве альтернативы гиперболическая аномалия ЧАС) является:^[2]

${ displaystyle cosh {E} = {{ cos { theta} + e} over {1 + e cdot cos { theta}}}}$ или же ${ displaystyle tan { frac { theta} {2}} = { sqrt { frac {e + 1} {e-1}}} cdot tanh { frac {E} {2}}}$ или же ${ displaystyle tanh { frac {E} {2}} = { sqrt { frac {e-1} {e + 1}}} cdot tan { frac { theta} {2}}}$

Эксцентрическая аномалия E относится к средняя аномалия M к Уравнение Кеплера:

${ Displaystyle M = е зп E-E}$

Средняя аномалия пропорциональна времени

${ displaystyle M = { sqrt { frac { mu} {- a ^ {3}}}}. (t- tau),}$ куда μ это гравитационный параметр и а это большая полуось орбиты.

Угол траектории полета

Угол траектории полета (φ) - это угол между направлением скорости и перпендикуляром к радиальному направлению, поэтому он равен нулю в перицентре и стремится к 90 градусам на бесконечности.

${ Displaystyle загар ( фи) = { гидроразрыва {е cdot грех тета} {1 + е cdot соз тета}}}$

Скорость

При стандартных предположениях орбитальная скорость (${ displaystyle v ,}$) тела, движущегося по гиперболическая траектория можно вычислить из vis-viva уравнение в качестве:

${ displaystyle v = { sqrt { mu left ({2 over {r}} - {1 over {a}} right)}}}$

куда:

• ${ displaystyle mu ,}$ является стандартный гравитационный параметр,
• ${ Displaystyle г ,}$ - радиальное расстояние орбитального тела от центральный орган,
• ${ Displaystyle а , !}$ это (отрицательный) большая полуось.

При стандартных предположениях в любой позиции на орбите для орбитальная скорость (${ displaystyle v ,}$), местный скорость убегания (${ displaystyle {v_ {esc}} ,}$) и гиперболической избыточной скорости (${ Displaystyle v _ { infty} , !}$):

${ displaystyle v ^ {2} = {v_ {esc}} ^ {2} + {v _ { infty}} ^ {2}}$

Обратите внимание: это означает, что относительно небольшая дополнительная дельта-v выше, чем необходимо для ускорения до скорости убегания, получается относительно большая скорость на бесконечности. Например, в месте, где скорость эвакуации составляет 11,2 км / с, прибавление 0,4 км / с дает гиперболическую избыточную скорость 3,02 км / с.

${ displaystyle { sqrt {11.6 ^ {2} -11.2 ^ {2}}} = 3.02}$

Это пример Эффект Оберта. Верно и обратное - тело не нужно сильно замедлять по сравнению с его гиперболической избыточной скоростью (например, за счет атмосферного сопротивления около периапсиса), чтобы скорость упала ниже скорости убегания и, таким образом, тело могло быть захвачено.

Радиальная гиперболическая траектория

Радиальная гиперболическая траектория - это непериодическая траектория по прямой где относительная скорость двух объектов всегда превышает скорость убегания. Возможны два случая: тела удаляются друг от друга или навстречу друг другу. Это гиперболическая орбита с малой полуосью = 0 и эксцентриситетом = 1. Хотя эксцентриситет равен 1, это не параболическая орбита.

Релятивистская проблема двух тел

В контексте задача двух тел в общей теории относительности, траектории объектов с достаточной энергией, чтобы избежать гравитационного притяжения другого, больше не имеют формы гиперболы. Тем не менее, термин «гиперболическая траектория» все еще используется для описания орбит этого типа.

Смотрите также

• Орбита
• Орбитальное уравнение
• Орбита Кеплера
• Список орбит
• Планетарный пролет
• Гиперболический астероид
• Гиперболическая комета

Рекомендации

внешняя ссылка

• https://web.archive.org/web/20081008041919/http://homepage.mac.com/sjbradshaw/msc/traject.html
• https://web.archive.org/web/20050316084931/http://www.go.ednet.ns.ca/~larry/orbits/ellipse.html
• https://web.archive.org/web/20120204054322/http://www.braeunig.us/space/orbmech.htm#hyperbolic