Уравнение ракеты Циолковского - Википедия - Tsiolkovsky rocket equation

Диаграмма, показывающая массовые отношения график зависимости от его конечной скорости, рассчитанной с использованием уравнения Циолковского.

Часть серии по
Астродинамика
Орбитальная механика
Параметры орбиты Апсис Аргумент периапсиса Азимут Эксцентриситет Наклон Средняя аномалия Орбитальные узлы Большая полуось Истинная аномалия
Виды двухчастичные орбиты, к эксцентриситет Круговая орбита Эллиптическая орбита Переходная орбита (Переходная орбита Хомана Биэллиптическая переходная орбита ) Параболическая орбита Гиперболическая орбита Радиальная орбита Затухающая орбита
Уравнения Динамическое трение Скорость убегания Уравнение Кеплера Законы движения планет Кеплера Орбитальный период Орбитальная скорость Поверхностная гравитация Удельная орбитальная энергия Уравнение Vis-viva
Небесная механика
Гравитационные воздействия Барицентр Сфера холма Возмущения Сфера влияния
N-тела орбиты Лагранжевые точки (Гало-орбиты ) Орбиты Лиссажу Ляпуновские орбиты
Инженерия и эффективность
Предполетная инженерия Соотношение масс Доля полезной нагрузки Массовая доля топлива Уравнение ракеты Циолковского
Меры эффективности Помощь гравитации Эффект Оберта

В Уравнение ракеты Циолковского, классическое ракетное уравнение, или же уравнение идеальной ракеты математическое уравнение, описывающее движение транспортных средств, которые следуют основному принципу ракета: устройство, которое может применять к себе ускорение, используя толкать выбрасывая часть своей массы с высокой скорость таким образом может двигаться из-за сохранение импульса.

${ displaystyle Delta v = v _ { text {e}} ln { frac {m_ {0}} {m_ {f}}} = I _ { text {sp}} g_ {0} ln { гидроразрыв {m_ {0}} {m_ {f}}}}$

куда:

${ displaystyle Delta v }$ является дельта-v - максимальное изменение скорость автомобиля (без воздействия внешних сил).

${ displaystyle m_ {0}}$ - начальная полная масса, включая пропеллент, также известная как мокрая масса.

${ displaystyle m_ {f}}$ это окончательная общая масса без пропеллента, также известная как сухая масса.

${ displaystyle v _ { text {e}} = I _ { text {sp}} g_ {0}}$ это эффективная скорость истечения, куда:

${ displaystyle I _ { text {sp}}}$ это удельный импульс в измерении времени.

${ displaystyle g_ {0}}$ является стандартная сила тяжести.

${ displaystyle ln}$ это натуральный логарифм функция.

История

Уравнение названо в честь русский ученый Константин Циолковский (Русский: Константин Циолковский), который независимо вывел его и опубликовал в своей работе 1903 года.^[1] Уравнение было выведено ранее Британский математик Уильям Мур в 1810 г.,^[2] и позже опубликован в отдельной книге в 1813 году.^[3] Министр Уильям Лейтч, который был способным ученым, также независимо получил основы ракетной техники в 1861 году.

Роберт Годдард в Америке независимо разработал уравнение в 1912 году, когда начал свои исследования по усовершенствованию ракетных двигателей для возможных космических полетов. Герман Оберт в Европе независимо вывел уравнение около 1920 года, когда изучал возможность космических путешествий.

В то время как вывод уравнения ракеты является несложным исчисление Циолковский удостоился чести первым применить его к вопросу о том, могут ли ракеты развивать скорость, необходимую для космическое путешествие.

Вывод

Самый популярный вывод

Рассмотрим следующую систему: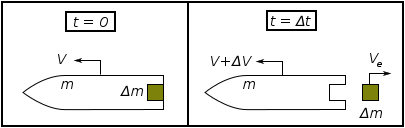

В следующем выводе «ракета» означает «ракету и все ее несгоревшее топливо».

Второй закон движения Ньютона связывает внешние силы (${ displaystyle F_ {i} ,}$) к изменению количества движения всей системы (включая ракету и выхлоп) следующим образом:

${ displaystyle sum F_ {i} = lim _ { Delta t to 0} { frac {P_ {2} -P_ {1}} { Delta t}}}$

куда ${ Displaystyle P_ {1} ,}$ это импульс ракеты во времени ${ displaystyle t = 0}$:

${ displaystyle P_ {1} = left ({m + Delta m} right) V}$

и ${ Displaystyle P_ {2} ,}$ импульс ракеты и исчерпанная масса в момент времени ${ displaystyle t = Delta t ,}$:

${ displaystyle P_ {2} = m left (V + Delta V right) + Delta mV _ { text {e}}}$

и где по отношению к наблюдателю:

${ Displaystyle V ,}$ скорость ракеты в момент времени ${ displaystyle t = 0}$

${ Displaystyle V + Delta V ,}$ скорость ракеты в момент времени ${ displaystyle t = Delta t ,}$

${ displaystyle V _ { text {e}} ,}$ - скорость массы, добавляемой к выхлопу (и теряемой ракетой) за время ${ displaystyle Delta t ,}$

${ displaystyle m + Delta m ,}$ это масса ракеты во время ${ displaystyle t = 0}$

${ Displaystyle м ,}$ это масса ракеты во время ${ displaystyle t = Delta t ,}$

Скорость выхлопа ${ displaystyle V _ { text {e}}}$ в кадре наблюдателя связана со скоростью истечения в раме ракеты. ${ displaystyle v _ { text {e}}}$ на (поскольку скорость истечения в отрицательном направлении)

${ displaystyle V _ { text {e}} = V-v _ { text {e}}}$

Решение урожайности:

${ Displaystyle P_ {2} -P_ {1} = m Delta V-v _ { text {e}} Delta m ,}$

и, используя ${ displaystyle dm = - Delta m}$, так как выброс положительного ${ displaystyle Delta m}$ приводит к снижению массы,

${ displaystyle sum F_ {i} = m { frac {dV} {dt}} + v _ { text {e}} { frac {dm} {dt}}}$

Если нет внешних сил, то ${ Displaystyle сумма F_ {я} = 0}$ (сохранение количества движения ) и

${ displaystyle m { frac {dV} {dt}} = - v _ { text {e}} { frac {dm} {dt}}}$

Предполагая ${ displaystyle v _ { text {e}} ,}$ постоянна, это можно интегрировать следующим образом:

${ displaystyle int _ {V} ^ {V + Delta V} , mathrm {d} V = {- v_ {e}} int _ {m_ {0}} ^ {m_ {1}} { гидроразрыв {1} {m}} , mathrm {d} m}$

Тогда это дает

${ displaystyle Delta V = v _ { text {e}} ln { frac {m_ {0}} {m_ {1}}}}$

или эквивалентно

${ displaystyle m_ {1} = m_ {0} e ^ {- Delta V / v _ { text {e}}}}$ или же ${ displaystyle m_ {0} = m_ {1} e ^ { Delta V / v _ { text {e}}}}$ или же ${ displaystyle m_ {0} -m_ {1} = m_ {1} left (e ^ { Delta V / v _ { text {e}}} - 1 right)}$

куда ${ displaystyle m_ {0}}$ - начальная полная масса, включая топливо, ${ displaystyle m_ {1}}$ окончательная общая масса, и ${ displaystyle v _ { text {e}}}$ скорость истечения ракеты относительно ракеты ( удельный импульс, или, если измерять во времени, умноженное на сила тяжести - ускорение на Земле).

Значение ${ displaystyle m_ {0} -m_ {1}}$ - общая масса израсходованного топлива и, следовательно:

${ displaystyle M_ {f} = 1 - { frac {m_ {1}} {m_ {0}}} = 1-e ^ {- Delta V / v _ { text {e}}}}$

куда ${ displaystyle M_ {f}}$ это массовая доля пороха (часть начальной общей массы, которая тратится как рабочая масса ).

${ displaystyle Delta V ,}$ (дельта v ) представляет собой интегрирование во времени величины ускорения, создаваемого ракетным двигателем (каким было бы фактическое ускорение, если бы внешние силы отсутствовали). В свободном пространстве, для случая ускорения в направлении скорости, это увеличение скорости. В случае ускорения в обратном направлении (замедления) это уменьшение скорости. Конечно, сила тяжести и сопротивление также ускоряют транспортное средство, и они могут добавлять или уменьшать изменение скорости транспортного средства. Следовательно, delta-v обычно не является фактическим изменением скорости или скорости транспортного средства.

Прочие производные

Импульсный

Уравнение также может быть получено из основного интеграла ускорения в виде силы (тяги) по массе, представив уравнение дельта-v следующим образом:

${ displaystyle Delta v = int _ {t0} ^ {t1} { frac {| T |} {{m_ {0}} - {t} Delta {m}}} ~ dt}$

где Т - тяга, ${ displaystyle m_ {0}}$ - начальная (мокрая) масса и ${ displaystyle Delta m}$ - начальная масса минус конечная (сухая) масса,

и понимая, что интеграл равнодействующей силы с течением времени представляет собой общий импульс, предполагая, что сила тяги является единственной задействованной силой,

${ Displaystyle int _ {t0} ^ {t1} F ~ dt = J}$

Интеграл оказывается:

${ displaystyle J ~ { frac { ln ({m_ {0}}) - ln ({m_ {1}})} { Delta m}}}$

Понимая, что импульс при изменении массы эквивалентен силе, действующей на массовый расход топлива (p), что само по себе эквивалентно скорости истечения,

${ displaystyle { frac {J} { Delta m}} = { frac {F} {p}} = V _ { rm {exh}}}$

интеграл можно приравнять к

${ displaystyle Delta v = V _ { rm {exh}} ~ ln left ({ frac {m_ {0}} {m_ {1}}} right)}$

На основе ускорения

Представьте себе ракету, покоящуюся в космосе, без приложения к ней сил (Первый закон движения Ньютона ). С момента запуска двигателя (часы установлены на 0) ракета выбрасывает массу газа с постоянный массовый расход R (кг / с) и при скорость истечения относительно ракеты v_е (РС). Это создает постоянную силу F запуск ракеты, равной R × v_е. Ракета подвергается воздействию постоянной силы, но ее общая масса неуклонно уменьшается, поскольку она выбрасывает газ. В соответствии с Второй закон движения Ньютона, его ускорение в любой момент т это его движущая сила F делится на его текущую массу м:

${ displaystyle ~ a = { frac {dv} {dt}} = - { frac {F} {m (t)}} = - { frac {Rv _ { text {e}}} {m (t )}}}$

Теперь масса топлива, изначально имеющегося на борту ракеты, равна м₀ - м₁. Для постоянного массового расхода р поэтому потребуется время T = (м₀ - м₁)/Р чтобы сжечь все это топливо. Интегрируя обе части уравнения по времени из 0 к Т (и отмечая, что R = dm / dt допускает замену справа), получаем

${ displaystyle ~ Delta v = v_ {1} -v_ {0} = - v _ { text {e}} left [ ln m_ {1} - ln m_ {0} right] = ~ v_ { text {e}} ln left ({ frac {m_ {0}} {m_ {1}}} right).}$

Предел выталкивания «гранул» конечной массы

Уравнение ракеты также может быть получено как предельный случай изменения скорости для ракеты, которая выбрасывает свое топливо в виде ${ displaystyle N}$ пеллеты последовательно, как ${ Displaystyle N rightarrow infty}$, с эффективной скоростью выхлопа ${ displaystyle v _ { rm {eff}}}$ так что механическая энергия, полученная на единицу массы топлива, определяется выражением ${ Displaystyle { tfrac {1} {2}} v _ { rm {eff}} ^ {2}}$.

Позволять ${ displaystyle phi}$ - начальная массовая доля топлива на борту и ${ displaystyle m_ {0}}$начальная заправленная масса ракеты. Разделите общую массу топлива ${ displaystyle phi m_ {0}}$ в ${ displaystyle N}$ дискретные гранулы каждой массы ${ displaystyle phi m_ {0} / N}$. Из сохранения импульса при выбросе ${ displaystyle j}$пеллеты, общее изменение скорости можно представить как сумму^[4]

${ displaystyle Delta v = v _ { rm {eff}} sum _ {j = 1} ^ {j = N} { frac { phi / N} { sqrt {(1-j phi / N ) (1-j phi / N + phi / N)}}}}$

Обратите внимание, что для больших ${ displaystyle N}$ последний член в знаменателе ${ displaystyle phi / N ll 1}$ и им можно пренебречь, чтобы дать

${ displaystyle Delta v приблизительно v _ { rm {eff}} sum _ {j = 1} ^ {j = N} { frac { phi / N} {1-j phi / N}} = v _ { rm {eff}} sum _ {j = 1} ^ {j = N} { frac { Delta x} {1-x_ {j}}}}$ куда ${ displaystyle Delta x = { frac { phi} {N}}}$ и ${ displaystyle x_ {j} = { frac {j phi} {N}}}$.

В качестве ${ Displaystyle N rightarrow infty}$ это Сумма Римана становится определенным интегралом

${ displaystyle lim _ {N to infty} Delta v = v _ { rm {eff}} int _ {0} ^ { phi} { frac {dx} {1-x}} = v_ { rm {eff}} ln { frac {1} {1- phi}} = v _ { rm {eff}} ln { frac {m_ {0}} {m_ {1}}}}$ так как оставшаяся масса ракеты равна ${ displaystyle m_ {1} = m_ {0} (1- phi)}$.

Специальная теория относительности

Если специальная теория относительности с учетом, следующее уравнение может быть получено для релятивистская ракета,^[5] с ${ displaystyle Delta v}$ снова обозначает конечную скорость ракеты (после выброса всей ее реакционной массы и уменьшения до массы покоя ${ displaystyle m_ {1}}$) в инерциальная система отсчета где ракета стартовала в состоянии покоя (масса покоя, включая топливо ${ displaystyle m_ {0}}$ изначально), и ${ displaystyle c}$ стоя за скорость света в вакууме:

${ displaystyle { frac {m_ {0}} {m_ {1}}} = left [{ frac {1 + { frac { Delta v} {c}}} {1 - { frac { Дельта v} {c}}}} right] ^ { frac {c} {2v _ { text {e}}}}}$

Письмо ${ displaystyle { frac {m_ {0}} {m_ {1}}}}$ в качестве ${ displaystyle R}$ позволяет переформулировать это уравнение как

${ displaystyle { frac { Delta v} {c}} = { frac {R ^ { frac {2v _ { text {e}}} {c}} - 1} {R ^ { frac {2v_ { text {e}}} {c}} + 1}}}$

Затем, используя личность ${ displaystyle R ^ { frac {2v _ { text {e}}} {c}} = exp left [{ frac {2v _ { text {e}}} {c}} ln R right ]}$ (здесь "exp" обозначает экспоненциальная функция; смотрите также Натуральный логарифм а также "силовая" идентичность на Логарифмические тождества ) и тождество ${ displaystyle tanh x = { frac {e ^ {2x} -1} {e ^ {2x} +1}}}$ (видеть Гиперболическая функция ), это эквивалентно

${ displaystyle Delta v = c tanh left ({ frac {v _ { text {e}}} {c}} ln { frac {m_ {0}} {m_ {1}}} right )}$

Условия уравнения

Дельта-v

Дельта-v (в прямом смысле "изменять в скорость "), обозначаемый как Δv и произносится дельта-вее, как используется в динамика полета космического корабля, является мерой импульс который необходим для выполнения маневра, такого как запуск или посадка на планете или луне, или в космосе орбитальный маневр. Это скаляр который имеет единицы скорость. В данном контексте это нет так же, как физическое изменение скорости автомобиля.

Дельта-v производится реактивными двигателями, такими как ракетные двигатели и пропорционален толкать на единицу массы и время горения, и используется для определения массы пропеллент требуется для данного маневра через уравнение ракеты.

Для нескольких маневров дельта-v суммирует линейно.

Для межпланетных миссий дельта-v часто изображается на свинина который отображает требуемую дельту миссии-v в зависимости от даты запуска.

Массовая доля

В аэрокосмическая техника, массовая доля топлива - это часть массы транспортного средства, которая не достигает пункта назначения, обычно используемая как мера характеристик транспортного средства. Другими словами, массовая доля топлива - это отношение массы топлива к начальной массе транспортного средства. В космическом корабле местом назначения обычно является орбита, а для самолетов - это место посадки. Более высокая массовая доля означает меньший вес конструкции. Еще одна связанная мера - это доля полезной нагрузки, который представляет собой долю полезной нагрузки от начального веса.

Эффективная скорость выхлопа

Эффективная скорость выхлопа часто определяется как удельный импульс и они связаны друг с другом:

${ displaystyle v _ { text {e}} = g_ {0} I _ { text {sp}},}$

куда

${ displaystyle I _ { text {sp}}}$ удельный импульс в секундах,

${ displaystyle v _ { text {e}}}$ удельный импульс, измеренный в РС, что совпадает с эффективной скоростью выхлопа, измеренной в м / с (или фут / с, если g выражается в фут / с²),

${ displaystyle g_ {0}}$ это стандартная сила тяжести, 9.80665 РС² (в Имперские единицы 32.174 фут / с²).

Применимость

Уравнение ракеты охватывает основы физики полета ракеты в одном коротком уравнении. Это также справедливо для реактивных ракетных машин, когда эффективная скорость выхлопа постоянна, и может быть суммировано или интегрировано, когда эффективная скорость истечения изменяется. Уравнение ракеты учитывает только силу реакции ракетного двигателя; он не включает другие силы, которые могут действовать на ракету, такие как аэродинамический или же гравитационный силы. Таким образом, при использовании его для расчета потребности в топливе для запуска с (или механического спуска на) планеты с атмосферой, влияние этих сил должно быть включено в требование дельта-V (см. Примеры ниже). В том, что было названо «тиранией ракетного уравнения», есть предел количеству полезная нагрузка которые может нести ракета, поскольку большее количество топлива увеличивает общий вес и, таким образом, также увеличивает расход топлива.^[6] Уравнение не применяется к неракетные системы Такие как аэротормоз, пушки, космические лифты, петли запуска, тросовый двигатель или же легкие паруса.

Уравнение ракеты можно применить к орбитальные маневры чтобы определить, сколько топлива необходимо, чтобы перейти на конкретную новую орбиту, или чтобы найти новую орбиту в результате определенного сгорания топлива. Применительно к орбитальным маневрам предполагается импульсивный маневр, при котором порох выгружается, а дельта-v применяется мгновенно. Это предположение относительно точно для кратковременных ожогов, таких как корректировки на середине курса и маневры по орбитальной установке. По мере увеличения продолжительности горения результат становится менее точным из-за воздействия силы тяжести на транспортное средство в течение всего маневра. Для малой тяги и продолжительной тяги, например электрическая силовая установка, более сложный анализ, основанный на распространении вектора состояния космического аппарата и интегрировании тяги, используется для прогнозирования орбитального движения.

Примеры

Предположим, что скорость истощения составляет 4500 метров в секунду (15000 футов / с) и ${ displaystyle Delta v}$ 9700 метров в секунду (32000 футов / с) (от Земли до ЛЕО, включая ${ displaystyle Delta v}$ для преодоления силы тяжести и аэродинамического сопротивления).

• Одноступенчатый на орбиту ракета: ${ displaystyle 1-e ^ {- 9,7 / 4,5}}$ = 0,884, следовательно, 88,4% начальной общей массы должно быть пропеллентом. Остальные 11,6% приходятся на двигатели, бак и полезную нагрузку.
• Двухступенчатый на орбиту: предположим, что первый этап должен обеспечить ${ displaystyle Delta v}$ 5000 метров в секунду (16000 футов / с); ${ displaystyle 1-e ^ {- 5.0 / 4.5}}$ = 0,671, следовательно, 67,1% начальной общей массы должно быть пропеллентом для первой ступени. Оставшаяся масса 32,9%. После утилизации первой ступени масса остается равной 32,9% за вычетом массы танка и двигателей первой ступени. Предположим, что это 8% от начальной общей массы, тогда остается 24,9%. Второй этап должен обеспечить ${ displaystyle Delta v}$ 4700 метров в секунду (15000 футов / с); ${ displaystyle 1-e ^ {- 4,7 / 4,5}}$ = 0,648, следовательно, 64,8% оставшейся массы должно быть ракетным, что составляет 16,2% от исходной общей массы, а 8,7% остается для танка и двигателей второй ступени, полезной нагрузки и в случае космического челнока. , а также орбитальный аппарат. Таким образом, вместе 16,7% исходной стартовой массы доступно для все двигатели, танки и полезная нагрузка.

Этапы

В случае последовательного проталкивания ступени ракеты, уравнение применяется для каждой ступени, где для каждой ступени начальная масса в уравнении - это полная масса ракеты после отбрасывания предыдущей ступени, а конечная масса в уравнении - это общая масса ракеты непосредственно перед отбрасыванием ступени. обеспокоенный. Для каждого этапа удельный импульс может быть разным.

Например, если 80% массы ракеты составляет топливо первой ступени, 10% - это сухая масса первой ступени, а 10% - оставшаяся ракета, то

${ displaystyle { begin {align} Delta v & = v _ { text {e}} ln {100 over 100-80} & = v _ { text {e}} ln 5 & = 1.61v _ { text {e}}. конец {выровнено}}}$

С тремя одинаковыми, а затем и меньшими ступенями с одинаковым ${ displaystyle v _ { text {e}}}$ для каждого этапа у нас есть

${ displaystyle Delta v = 3v _ { text {e}} ln 5 = 4.83v _ { text {e}}}$

а полезная нагрузка составляет 10% × 10% × 10% = 0,1% от начальной массы.

Сопоставимый ССТО ракета, также имеющая 0,1% полезной нагрузки, могла иметь массу 11,1% для топливных баков и двигателей и 88,8% для топлива. Это даст

${ displaystyle Delta v = v _ { text {e}} ln (100 / 11.2) = 2.19v _ { text {e}}.}$

Если двигатель новой ступени зажигается до того, как предыдущая ступень была выброшена, и одновременно работающие двигатели имеют другой удельный импульс (как это часто бывает с твердотопливными ракетными ускорителями и ступенью на жидком топливе), ситуация усложняется.

Распространенные заблуждения

Если рассматривать как система переменной массы, ракету нельзя непосредственно проанализировать с помощью Второй закон движения Ньютона потому что закон действует только для систем с постоянной массой.^[7][8][9] Может вызвать недоумение то, что уравнение ракеты Циолковского похоже на уравнение уравнение релятивистской силы ${ Displaystyle F = dp / dt = m ; dv / dt + v ; dm / dt}$. Используя эту формулу с ${ Displaystyle м (т)}$ поскольку изменяющаяся масса ракеты, кажется, выводит уравнение ракеты Циолковского, но этот вывод неверен. Обратите внимание, что эффективная скорость истечения ${ displaystyle v _ { text {e}}}$ даже не фигурирует в этой формуле.

Смотрите также

• Бюджет Delta-v
• Соотношение масс
• Эффект Оберта применение дельта-v в гравитационный колодец увеличивает конечную скорость
• Релятивистская ракета
• Обратимость орбит
• Движение космического корабля
• Системы переменной массы
• Рабочая масса

Рекомендации

внешняя ссылка

• Как вывести уравнение ракеты
• Калькулятор относительности - Изучите уравнения ракеты Циолковского
• График и калькулятор уравнений ракеты Циолковского в WolframAlpha