Долгота восходящего узла - Longitude of the ascending node

Долгота восходящий узел (ярко-зеленый) как часть диаграммы параметры орбиты.

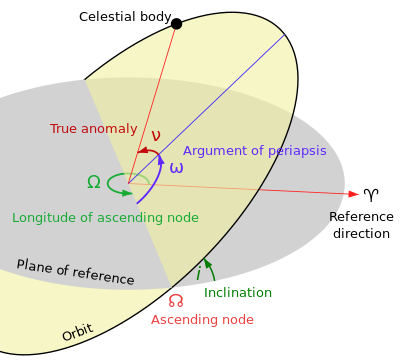
В долгота восходящего узла (☊ или Ω) является одним из орбитальные элементы используется для указания орбита объекта в космосе. Это угол от заданного опорного направления, называется начало долготы, в направлении восходящий узел, как измерено в указанном базовая плоскость.^[1] Восходящий узел - это точка, в которой орбита объекта проходит через плоскость отсчета, как видно на соседнем изображении. Обычно используемые опорные плоскости и точки отсчета долготы включают:

• За геоцентрические орбиты, земной шар с экваториальный плоскость в качестве базовой плоскости, а Первая точка Овна как начало долготы. В этом случае долготу также называют прямое восхождение восходящего узла (РААН). Угол измеряется на восток (или, если смотреть со стороны север, против часовой стрелки ) от Первая точка Овна к узлу.^[2][3]
• За гелиоцентрические орбиты, то эклиптика как исходная плоскость, а Первая точка Овна как начало долготы. Угол измеряется против часовой стрелки (если смотреть с севера от эклиптики) от Первой точки Овна до узла.^[2]
• Для орбит вне Солнечная система, касательная плоскость к небесная сфера в интересной точке (называемой самолет неба ) в качестве плоскости отсчета, а север (т. е. перпендикулярная проекция направления от наблюдателя к Северный небесный полюс на плоскость неба) как начало долготы. Угол измеряется на восток (или, как видит наблюдатель, против часовой стрелки) от севера до узла.^{[4], стр. 40, 72, 137;[5], гл. 17.}

В случае двойная звезда известно только из визуальных наблюдений, невозможно сказать, какой узел восходящий, а какой нисходящий. В этом случае регистрируемый параметр орбиты просто обозначается долгота узла, Ω, и представляет собой долготу любого узла, имеющего долготу от 0 до 180 градусов.^{[5], гл. 17;[4], п. 72.}

Расчет по векторам состояния

В астродинамика, долготу восходящего узла можно рассчитать по удельный относительный угловой момент вектор час следующее:

${ displaystyle { begin {align} mathbf {n} & = mathbf {k} times mathbf {h} = (- h_ {y}, h_ {x}, 0) Omega & = { begin {case} arccos {{n_ {x}} over { mathbf { left | n right |}}}, & n_ {y} geq 0; 2 pi - arccos {{n_ {x}} over { mathbf { left | n right |}}}, & n_ {y} <0. end {ases}} end {выравнивается}}}$

Здесь, п=<п_Икс, п_у, п_z> - вектор, указывающий на восходящий узел. Базовая плоскость считается ху-плоскость, а начало долготы принимается положительным Икс-ось. k - единичный вектор (0, 0, 1), который является нормальным вектором к ху базовая плоскость.

За неисклонные орбиты (с склонность равно нулю), Ω не определено. Затем для вычислений он по соглашению устанавливается равным нулю; то есть восходящий узел находится в заданном направлении, что эквивалентно сдача п указывать на позитив Икс-ось.

Смотрите также

• Равноденствие
• Кеплеровские орбиты
• Орбитальный узел
• Возмущение плоскости орбиты может вызвать прецессия восходящего узла.

Рекомендации