Долгота перицентра - Longitude of the periapsis

ϖ = Ω + ω в отдельных плоскостях.

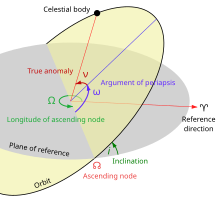
В небесная механика, то долгота перицентра, также называемый долгота перицентраорбитального тела является долгота (измеряется от точки весеннего равноденствия), в которой перицентр (максимальное приближение к центральному телу) произойдет, если орбита тела склонность были нулевыми. Обычно обозначается ϖ.

Для движения планеты вокруг Солнца это положение называется долгота перигелия ϖ, которая представляет собой сумму долготы восходящего узла Ω, и аргумент перигелия ω.^{[1][2]:с.672 и др.}

Долгота перицентра - это составной угол, часть которого измеряется в плоскость отсчета а остальное измеряется в плоскости орбита. Точно так же любой угол, полученный из долготы перицентра (например, средняя долгота и истинная долгота ) также будет составным.

Иногда термин долгота перицентра используется для обозначения ω, угол между восходящим узлом и перицентром. Этот термин особенно часто используется при обсуждении двойных звезд и экзопланет.^[3][4] Однако угол ω менее неоднозначно известен как угол аргумент перицентра.

Расчет по векторам состояния

ϖ это сумма долгота восходящего узла Ω (измерено в плоскости эклиптики) и аргумент перицентра ω (измерено в орбитальной плоскости):

${ displaystyle varpi = Omega + omega}$

которые получены из орбитальные векторы состояния.

Определение эклиптической долготы и широты перигелия для наклонных орбит

Определите следующее:

я, наклон

ω, аргумент перигелия

Ω, долгота восходящего узла

ε, наклон эклиптики (для стандартного равноденствия 2000,0 используйте 23,43929111 °)

Потом:

A = cos ω cos Ω - sin ω sin Ω cos i

B = cos ε (cos ω sin Ω + sin ω cos Ω cos i) - sin ε sin ω sin i

C = sin ε (cos ω sin Ω + sin ω cos Ω cos i) + cos ε sin ω sin i

Прямое восхождение α и склонение δ направления перигелия:

tan α = B/А

грех δ = C

Если A <0, добавьте 180 ° к α, чтобы получить правильный квадрант.

Эклиптическая долгота ϖ и широта перигелия b:

загар ϖ = sin α cos ε + tan δ sin ε/cos α

sin b = sin δ cos ε - cos δ sin ε sin α

Если cos (α) <0, добавьте 180 ° к ϖ, чтобы получить правильный квадрант.

В качестве примера использованы самые свежие цифры из Брауна (2017)^[5] для гипотетической Девятой Планеты с i = 30 °, ω = 136,92 ° и Ω = 94 °, тогда α = 237,38 °, δ = + 0,41 ° и ϖ = 235,00 °, b = + 19,97 ° (Браун фактически дает i, Ω и ϖ, из которых вычислялось ω).

Рекомендации

внешняя ссылка

• ^{[мертвая ссылка ]} Определение параметров орбиты Земли. Прошлая и будущая долгота перигелия Земли.