Возмущение (астрономия) - Perturbation (astronomy)

Возмущающие силы солнце на Луна в двух местах в орбита. Синие стрелки обозначают направление и величина гравитационной силы на земной шар. Применение этого к положению Земли и Луны не меняет положения относительно друг друга. Когда она вычитается из силы на Луне (черные стрелки), остается возмущающая сила (красные стрелки) на Луне относительно Земли. Поскольку возмущающая сила различается по направлению и величине на противоположных сторонах орбиты, она вызывает изменение формы орбиты.

Часть серии по
Астродинамика
Орбитальная механика
Параметры орбиты Апсис Аргумент периапсиса Азимут Эксцентриситет Наклон Средняя аномалия Орбитальные узлы Большая полуось Истинная аномалия
Виды двухчастичные орбиты, к эксцентриситет Круговая орбита Эллиптическая орбита Переходная орбита (Переходная орбита Хомана Биэллиптическая переходная орбита ) Параболическая орбита Гиперболическая орбита Радиальная орбита Затухающая орбита
Уравнения Динамическое трение Скорость убегания Уравнение Кеплера Законы движения планет Кеплера Орбитальный период Орбитальная скорость Поверхностная гравитация Удельная орбитальная энергия Уравнение Vis-viva
Небесная механика
Гравитационные воздействия Барицентр Сфера холма Возмущения Сфера влияния
N-тела орбиты Лагранжевые точки (Гало-орбиты ) Орбиты Лиссажу Ляпуновские орбиты
Инженерия и эффективность
Предполетная инженерия Соотношение масс Доля полезной нагрузки Массовая доля топлива Уравнение ракеты Циолковского
Меры эффективности Помощь гравитации Эффект Оберта

В астрономия, возмущение сложное движение массивное тело подчиняется силам, отличным от гравитационный влечение друг друга массивный тело.^[1] Другие силы могут включать в себя третье (четвертое, пятое и т. Д.) Тело, сопротивление, как из атмосфера, и притяжение вне центра сплюснутый или иначе деформированное тело.^[2]

Вступление

Изучение возмущений началось с первых попыток предсказания движения планет в небе. В древности причины оставались загадкой. Ньютон, в то время, когда он сформулировал свои законы движение и из гравитация применил их к первому анализу возмущений,^[2] осознавая сложные трудности их расчета.^[3] С тех пор многие великие математики обратили внимание на различные связанные с этим проблемы; на протяжении 18-19 веков существовала потребность в точных таблицах положения Луна и планеты за морское судоходство.

Сложные движения гравитационных возмущений могут быть разбиты. Гипотетическое движение, которому тело следует под действием гравитации только одного другого тела, обычно является коническая секция, и легко описываются методами геометрия. Это называется проблема двух тел, или невозмутимый Кеплеровская орбита. Разница между этим и реальным движением тела состоит в следующем: возмущения из-за дополнительных гравитационных эффектов оставшегося тела или тел. Если есть только одно другое существенное тело, то возмущенное движение будет проблема трех тел; если есть несколько других тел, это ппроблема тела. Общее аналитическое решение (математическое выражение для предсказания положений и движений в любое время в будущем) существует для проблемы двух тел; когда рассматривается более двух тел, аналитические решения существуют только для особых случаев. Даже проблема двух тел становится неразрешимой, если одно из тел имеет неправильную форму.^[4]

Меркурий орбитальной долготы и широты, с учетом Венера, Юпитер и все планеты Солнечная система, с интервалом 2,5 дня. Если бы не было возмущений, Меркурий оставался бы в центре перекрестия.

Большинство систем, которые включают в себя несколько гравитационных притяжений, представляют одно основное тело, которое доминирует по своим эффектам (например, звезда в случае звезды и ее планеты или планеты в случае планеты и ее спутника). Гравитационные эффекты других тел можно рассматривать как возмущения гипотетического невозмущенного движения планеты или спутник вокруг его основного тела.

Математический анализ

Общие возмущения

В методах общие волнения, общие дифференциальные уравнения движения или изменения орбитальные элементы, решаются аналитически, обычно расширения серии. Результат обычно выражается в терминах алгебраических и тригонометрических функций орбитальных элементов рассматриваемого тела и возмущающих тел. Это может применяться в целом ко многим различным наборам условий и не является специфическим для какого-либо конкретного набора гравитирующих объектов.^[5] Исторически в первую очередь исследовались общие возмущения. Классические методы известны как вариация элементов, вариация параметров или же вариация постоянных интегрирования. В этих методах считается, что тело всегда движется в коническая секция Однако коническое сечение постоянно меняется из-за возмущений. Если бы все возмущения прекратились в любой конкретный момент, тело продолжало бы в этом (теперь неизменном) коническом сечении бесконечно; эта коника известна как оскулирующая орбита и это орбитальные элементы в каждый конкретный момент времени - это то, что ищут методы общих возмущений.^[2]

Общие возмущения используют тот факт, что во многих задачах небесная механика орбита двух тел из-за возмущений изменяется довольно медленно; орбита двух тел - хорошее первое приближение. Общие возмущения применимы, только если возмущающие силы примерно на порядок меньше или меньше, чем сила тяжести первичного тела.^[4] в Солнечная система, это обычно так; Юпитер, второе по величине тело, имеет массу примерно 1/1000 массы тела солнце.

Общие методы возмущений предпочтительны для некоторых типов задач, так как легко найти источник определенных наблюдаемых движений. Это не обязательно так для особых возмущений; движения предсказывались бы с такой же точностью, но никакой информации о конфигурации возмущающих тел (например, орбитальный резонанс ), которые их вызвали, будут доступны.^[4]

Особые возмущения

В методах особые возмущения, числовые наборы данных, представляющие значения для положений, скоростей и ускоряющих сил на исследуемых телах, составляют основу численное интегрирование дифференциала уравнения движения.^[6] Фактически, положения и скорости изменяются напрямую, и не делается попыток вычислить кривые орбит или орбитальные элементы.^[2]

Специальные возмущения можно применить к любой задаче в небесная механика, так как не ограничивается случаями, когда возмущающие силы малы.^[4] Когда-то применяемые только к кометам и малым планетам, специальные методы возмущений теперь являются основой наиболее точных, генерируемых машинами. планетарные эфемериды великих астрономических альманахов.^[2][7] Специальные возмущения также используются для моделирование орбита с компьютерами.

Формулировка Коуэлла

Метод Коуэлла. Силы от всех возмущающих тел (черный и серый) суммируются, чтобы сформировать общую силу, действующую на тело. я (красный), и это численно интегрировано, начиная с начальной позиции ( эпоха оскала).

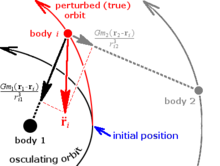
Формулировка Коуэлла (названная в честь Филип Х. Коуэлл, который с A.C.D. Кромеллин, использовавший аналогичный метод для предсказания возвращения кометы Галлея), возможно, является самым простым из специальных методов возмущений.^[8] В системе ${ displaystyle n}$ взаимно взаимодействующих тел, этот метод математически решает для Ньютоновский силы на теле ${ displaystyle i}$ суммируя индивидуальные взаимодействия с другими ${ displaystyle j}$ тела:

${ displaystyle mathbf { ddot {r}} _ {i} = sum _ { underset {j neq i} {j = 1}} ^ {n} {Gm_ {j} ( mathbf {r} _ {j} - mathbf {r} _ {i}) over r_ {ij} ^ {3}}}$

куда ${ Displaystyle mathbf { ddot {r}} _ {я}}$ это ускорение вектор тела ${ displaystyle i}$, ${ displaystyle G}$ это гравитационная постоянная, ${ displaystyle m_ {j}}$ это масса тела ${ displaystyle j}$, ${ Displaystyle mathbf {r} _ {я}}$ и ${ displaystyle mathbf {r} _ {j}}$ являются векторы положения объектов ${ displaystyle i}$ и ${ displaystyle j}$ соответственно, и ${ displaystyle r_ {ij}}$ это расстояние от объекта ${ displaystyle i}$ для объекта ${ displaystyle j}$. Все векторов ссылаясь на барицентр системы. Это уравнение разложено на компоненты в ${ displaystyle x}$, ${ displaystyle y}$, и ${ displaystyle z}$ и они интегрируются численно, чтобы сформировать новые векторы скорости и положения. Этот процесс повторяется столько раз, сколько необходимо. Преимущество метода Коуэлла - простота применения и программирования. Недостатком является то, что когда возмущения становятся большими по величине (например, когда объект приближается к другому), ошибки метода также становятся большими.^[9] Однако для многих проблем в небесная механика, этого никогда не бывает. Другой недостаток заключается в том, что в системах с доминирующим центральным телом, например, солнце, нужно носить много значащие цифры в арифметика из-за большой разницы в силах центрального тела и возмущающих тел, хотя современные компьютеры это далеко не то ограничение, которое было раньше.^[10]

Метод Энке

Метод Энке. Здесь сильно преувеличена малая разница δр (синий) между соприкасающейся невозмущенной орбитой (черный) и возмущенной орбитой (красный) численно интегрируется, начиная с начальной позиции ( эпоха оскала).

Метод Энке начинается с оскулирующая орбита в качестве эталона и численно интегрируется для решения отклонения от эталона как функции времени.^[11] Его преимущества заключаются в том, что возмущения, как правило, невелики по величине, поэтому интегрирование может выполняться более крупными шагами (что приводит к меньшим ошибкам), и метод намного меньше зависит от экстремальных возмущений. Его недостаток - сложность; он не может использоваться бесконечно без периодического обновления орбиты соприкосновения и продолжения оттуда, процесс, известный как исправление.^[9] Метод Энке аналогичен общему методу возмущения изменения элементов, за исключением того, что исправление выполняется через дискретные интервалы, а не непрерывно.^[12]

Сдача ${ displaystyle { boldsymbol { rho}}}$ быть радиус-вектор из оскулирующая орбита, ${ displaystyle mathbf {r}}$ радиус-вектор возмущенной орбиты, и ${ displaystyle delta mathbf {r}}$ отклонение от оскулирующей орбиты,

${ displaystyle delta mathbf {r} = mathbf {r} - { boldsymbol { rho}}}$, а уравнение движения из ${ displaystyle delta mathbf {r}}$ просто

(1)

${ displaystyle { ddot { delta mathbf {r}}} = mathbf { ddot {r}} - { boldsymbol { ddot { rho}}}}$.

(2)

${ Displaystyle mathbf { ddot {r}}}$ и ${ displaystyle { boldsymbol { ddot { rho}}}}$ это просто уравнения движения ${ displaystyle mathbf {r}}$ и ${ displaystyle { boldsymbol { rho}},}$

${ displaystyle mathbf { ddot {r}} = mathbf {a} _ { text {per}} - { mu over r ^ {3}} mathbf {r}}$ для возмущенной орбиты и

(3)

${ displaystyle { boldsymbol { ddot { rho}}} = - { mu over rho ^ {3}} { boldsymbol { rho}}}$ для невозмущенной орбиты,

(4)

куда ${ Displaystyle му = Г (М + м)}$ это гравитационный параметр с ${ displaystyle M}$ и ${ displaystyle m}$ то массы центрального тела и возмущенного тела, ${ Displaystyle mathbf {а} _ { текст {пер}}}$ возмущает ускорение, и ${ displaystyle r}$ и ${ displaystyle rho}$ величины ${ displaystyle mathbf {r}}$ и ${ displaystyle { boldsymbol { rho}}}$.

Подставляя из уравнений (3) и (4) в уравнение (2),

${ displaystyle { ddot { delta mathbf {r}}} = mathbf {a} _ { text {per}} + mu left ({{ boldsymbol { rho}} over rho ^ {3}} - { mathbf {r} over r ^ {3}} right),}$

(5)

которые теоретически можно проинтегрировать дважды, чтобы найти ${ displaystyle delta mathbf {r}}$. Поскольку соприкасающаяся орбита легко вычисляется двухчастичными методами, ${ displaystyle { boldsymbol { rho}}}$ и ${ displaystyle delta mathbf {r}}$ учитываются и ${ displaystyle mathbf {r}}$ можно решить. На практике количество в скобках, ${ displaystyle {{ boldsymbol { rho}} over rho ^ {3}} - { mathbf {r} over r ^ {3}}}$, представляет собой разность двух почти равных векторов, и необходимы дальнейшие манипуляции, чтобы избежать необходимости в дополнительных значащие цифры.^[13][14] Метод Энке получил более широкое распространение до появления современных компьютеры, когда много расчетов орбиты выполнялось на механические счетные машины.

Периодический характер

Симулятор гравитации сюжет смены орбитальный эксцентриситет из Меркурий, Венера, земной шар, и Марс в течение следующих 50 000 лет. 0 точка на этом графике - 2007 год.

В Солнечной системе многие возмущения одной планеты другой являются периодическими, состоящими из небольших импульсов каждый раз, когда планета проходит другую по своей орбите. Это заставляет тела следовать периодическим или квазипериодическим движениям, таким как Луна в ее сильно встревоженный орбита, который является предметом лунная теория. Этот периодический характер привел к открытие Нептуна в 1846 г. в результате его возмущения орбиты Уран.

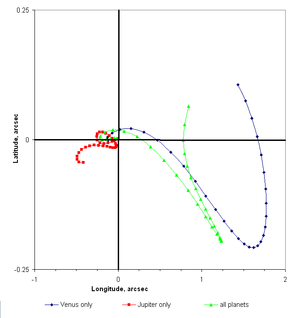
Продолжающиеся взаимные возмущения планет вызывают длительные квазипериодические изменения их орбитальные элементы, наиболее очевидно, когда орбитальные периоды двух планет почти синхронизированы. Например, пять орбит Юпитер (59,31 года) почти равно двум из Сатурн (58,91 года). Это вызывает большие возмущения обоих, с периодом 918 лет, времени, необходимого для небольшой разницы в их положениях на соединение сделать один полный круг, впервые обнаруженный Лаплас.^[2] Венера в настоящее время имеет орбиту с наименьшим эксцентриситет, т.е. он наиболее близок к круговой, всех планетных орбит. Через 25000 лет земной шар будет иметь более круговую (менее эксцентрическую) орбиту, чем Венера. Показано, что длительные периодические возмущения в пределах Солнечная система может стать хаотичным в течение очень длительного времени; при некоторых обстоятельствах один или несколько планеты может пересечь орбиту другого, что приведет к столкновениям.^[15]

Орбиты многих малых тел Солнечной системы, таких как кометы, часто сильно возмущены, особенно гравитационными полями газовые гиганты. Хотя многие из этих возмущений являются периодическими, другие - нет, и они, в частности, могут представлять аспекты хаотическое движение. Например, в апреле 1996 г. Юпитер гравитационное влияние вызвало период из Комета Хейла – Боппа Орбита России уменьшится с 4206 до 2380 лет, и это изменение не будет возвращаться ни на какой периодической основе.^[16]

Смотрите также

• Формирование и эволюция Солнечной системы
• Замороженная орбита
• Молния орбита
• Нереида одна из внешних лун Нептуна с высокой орбитальный эксцентриситет ~ 0,75 и часто возмущается
• Оскулирующая орбита
• Моделирование орбиты
• Орбитальный резонанс
• Правильные элементы орбиты
• Устойчивость Солнечной системы

Рекомендации

Библиография

• Бейт, Роджер Р .; Мюллер, Дональд Д .; Уайт, Джерри Э. (1971). Основы астродинамики. Нью-Йорк: Dover Publications. ISBN  0-486-60061-0.
• Моултон, Лесной Луч (1914). Введение в небесную механику (2-е изд. Перераб.). Макмиллан.
• Рой, А. Э. (1988). Орбитальное движение (3-е изд.). Издательский институт Физики. ISBN  0-85274-229-0.

Сноски

дальнейшее чтение

• P.E. Эль'Ясберг: Введение в теорию полета искусственных спутников Земли

внешняя ссылка

• Солекс (Альдо Витальяно) предсказания положения / орбиты / сближения Марса
• Гравитация Книга сэра Джорджа Бидделла Эйри 1884 года о гравитационном движении и возмущениях, в которой математика почти не использовалась или вообще не использовалась (at Книги Google )