Моделирование орбиты - Orbit modeling

Моделирование орбиты это процесс создания математических моделей для моделирования движения массивного тела при его движении в орбита вокруг другого массивного тела из-за сила тяжести. Другие силы, такие как гравитационное притяжение третичных тел, сопротивление воздуха, солнечное давление, или толчок от движущая сила системы обычно моделируются как вторичные эффекты. Прямое моделирование орбиты может раздвинуть пределы точность станка из-за необходимости моделировать небольшие возмущения на очень больших орбитах. Из-за этого, возмущение методы часто используются для моделирования орбиты с целью достижения большей точности.

Фон

Изучение орбитального движения и математическое моделирование орбит началось с первых попыток предсказания движения планет в небе, хотя в древние времена причины оставались загадкой. Ньютон, в то время, когда он сформулировал свои законы движение и из гравитация применил их к первому анализу возмущений,^[1] осознавая сложные трудности их расчета.^[1]С тех пор многие великие математики обратили внимание на различные связанные с этим проблемы; на протяжении XVIII и XIX веков существовала потребность в точных таблицах положения Луны и планет для навигации на море.

Сложные движения орбит можно разбить. Гипотетическое движение, которому тело следует под действием гравитации только одного другого тела, обычно является коническая секция, и легко моделируются методами геометрия. Это называется проблема двух тел, или невозмутимый Кеплеровская орбита. Различия между кеплеровской орбитой и реальным движением тела вызваны: возмущения. Эти возмущения вызваны силами, отличными от гравитационного эффекта между первичным и вторичным телом, и должны моделироваться для создания точного моделирования орбиты. Большинство подходов к моделированию орбиты моделируют проблему двух тел, а затем добавляют модели этих возмущающих сил и моделируют эти модели с течением времени. Возмущающие силы могут включать гравитационное притяжение со стороны других тел помимо первичного, солнечный ветер, сопротивление, магнитные поля и движущие силы.

Аналитические решения (математические выражения для прогнозирования положений и движений в любое время в будущем) для простых двухчастичных и проблемы с тремя телами существовать; не было найдено ни одного ппроблема тела за исключением некоторых особых случаев. Даже проблема двух тел становится неразрешимой, если одно из тел имеет неправильную форму.^[2]

Из-за сложности поиска аналитических решений большинства интересующих проблем компьютер моделирование и симуляция обычно используется для анализа орбитального движения. Коммерческие программные приложения, такие как Комплект спутниковых инструментов были созданы специально для моделирования орбит и траекторий космических аппаратов.

Модель кеплеровской орбиты

В своей простейшей форме модель орбиты может быть создана, если предположить, что задействованы только два тела, оба ведут себя как сферические точечные массы и что никакие другие силы не действуют на тела. В этом случае модель упрощается до Орбита Кеплера.

Кеплеровские орбиты следуют конические секции. Математическая модель орбиты, которая дает расстояние между центральным телом и вращающимся телом, может быть выражена как:

${ Displaystyle г ( ню) = { гидроразрыва {а (1-е ^ {2})} {1 + е соз ( ню)}}}$

Где:

${ displaystyle r}$ это расстояние

${ displaystyle a}$ это большая полуось, который определяет размер орбиты

${ displaystyle e}$ это эксцентриситет, определяющий форму орбиты

${ displaystyle nu}$ это истинная аномалия, который представляет собой угол между текущим положением орбитального объекта и его ближайшим к центральному телу положением на орбите (называемым перицентр )

В качестве альтернативы уравнение можно выразить как:

${ Displaystyle г ( ню) = { гидроразрыва {р} {1 + е соз ( ню)}}}$

Где ${ displaystyle p}$ называется полу-латусная прямая кишка кривой. Эта форма уравнения особенно полезна при работе с параболическими траекториями, у которых большая полуось бесконечна.

Альтернативный подход использует Исаак Ньютон с закон всемирного тяготения как определено ниже:

${ displaystyle F = G { frac {m_ {1} m_ {2}} {r ^ {2}}}}$

куда:

${ displaystyle F}$ величина силы тяжести между двумя точечными массами

${ displaystyle G}$ это гравитационная постоянная

${ displaystyle m_ {1}}$ масса первой точечной массы

${ displaystyle m_ {2}}$ масса второй точечной массы

${ displaystyle r}$ это расстояние между двумя точечными массами

Сделав дополнительное предположение, что масса первичного тела намного больше, чем масса вторичного тела, и подставив в формулу Ньютона второй закон движения, приводит к следующему дифференциальному уравнению

${ displaystyle { ddot { mathbf {r}}} = { frac {Gm_ {1}} {r ^ {2}}} mathbf { hat {r}}}$

Решение этого дифференциального уравнения приводит к кеплеровскому движению орбиты. На практике кеплеровские орбиты обычно полезны только для приближений первого порядка, особых случаев или в качестве базовой модели для возмущенной орбиты.

Методы моделирования орбиты

Модели орбит обычно распространяются во времени и пространстве с помощью специальных возмущение методы. Это выполняется сначала путем моделирования орбиты как кеплеровской орбиты. Затем в модель добавляются возмущения для учета различных возмущений, влияющих на орбиту.^[1]Специальные возмущения можно применить к любой задаче в небесная механика, так как не ограничивается случаями, когда возмущающие силы малы.^[2] Специальные методы возмущений являются основой наиболее точных машинно-генерируемых планетарные эфемериды.^[1]см., например, Эфемериды разработки лаборатории реактивного движения

Метод Коуэлла

Метод Коуэлла. Силы от всех возмущающих тел (черный и серый) суммируются, чтобы сформировать общую силу, действующую на тело. я (красный), и это численно интегрировано, начиная с начальной позиции ( эпоха оскала).

Метод Коуэлла, пожалуй, самый простой из специальных методов возмущений;^[3]математически, для ${ displaystyle n}$ взаимно взаимодействующие тела, Ньютоновский силы на теле ${ displaystyle i}$ от других тел ${ displaystyle j}$ просто суммируются таким образом,

${ displaystyle mathbf { ddot {r}} _ {i} = sum _ { underset {j neq i} {j = 1}} ^ {n} {Gm_ {j} ( mathbf {r} _ {j} - mathbf {r} _ {i}) over r_ {ij} ^ {3}}}$

куда

${ Displaystyle mathbf { ddot {r}} _ {я}}$ это ускорение вектор тела ${ displaystyle i}$

${ displaystyle G}$ это гравитационная постоянная

${ displaystyle m_ {j}}$ это масса тела ${ displaystyle j}$

${ Displaystyle mathbf {r} _ {я}}$ и ${ displaystyle mathbf {r} _ {j}}$ являются векторы положения объектов ${ displaystyle i}$ и ${ displaystyle j}$

${ displaystyle r_ {ij}}$ это расстояние от объекта ${ displaystyle i}$ для объекта ${ displaystyle j}$

со всем векторов ссылаясь на барицентр системы. Это уравнение разложено на компоненты в ${ displaystyle x}$, ${ displaystyle y}$, ${ displaystyle z}$ и они численно интегрируются для формирования новых векторов скорости и положения по мере продвижения моделирования во времени. Преимущество метода Коуэлла - простота применения и программирования. Недостатком является то, что когда возмущения становятся большими по величине (например, когда объект приближается к другому), ошибки метода также становятся большими.^[4]Другой недостаток заключается в том, что в системах с доминирующим центральным телом, например, солнце, нужно носить много значащие цифры в арифметика из-за большой разницы в силах центрального тела и возмущающих тел.^[5]

Метод Энке

Метод Энке. Здесь сильно преувеличена малая разница δр (синий) между соприкасающейся невозмущенной орбитой (черный) и возмущенной орбитой (красный) численно интегрируется, начиная с начальной позиции ( эпоха оскала).

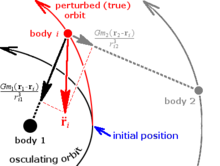
Метод Энке начинается с оскулирующая орбита в качестве эталона и численно интегрируется для решения отклонения от эталона как функции времени.^[6]Его преимущества заключаются в том, что возмущения, как правило, невелики по величине, поэтому интегрирование может выполняться более крупными шагами (что приводит к меньшим ошибкам), и метод гораздо меньше подвержен влиянию экстремальных возмущений, чем метод Коуэлла. Его недостаток - сложность; его нельзя использовать бесконечно, не обновляя время от времени оскулирующую орбиту и продолжая оттуда, процесс, известный как исправление.^[4][7]

Сдача ${ displaystyle { boldsymbol { rho}}}$ быть радиус-вектор из оскулирующая орбита, ${ displaystyle mathbf {r}}$ радиус-вектор возмущенной орбиты, и ${ displaystyle delta mathbf {r}}$ отклонение от оскулирующей орбиты,

${ displaystyle delta mathbf {r} = mathbf {r} - { boldsymbol { rho}},}$ и уравнение движения из ${ displaystyle delta mathbf {r}}$ просто

(1)

${ displaystyle { ddot { delta mathbf {r}}} = mathbf { ddot {r}} - { boldsymbol { ddot { rho}}}.}$

(2)

${ Displaystyle mathbf { ddot {r}}}$ и ${ displaystyle { boldsymbol { ddot { rho}}}}$ это просто уравнения движения ${ displaystyle mathbf {r}}$ и ${ displaystyle { boldsymbol { rho}}}$,

${ displaystyle mathbf { ddot {r}} = mathbf {a} _ { text {per}} - { mu over r ^ {3}} mathbf {r}}$ для возмущенной орбиты и

(3)

${ displaystyle { boldsymbol { ddot { rho}}} = - { mu over rho ^ {3}} { boldsymbol { rho}}}$ для невозмущенной орбиты,

(4)

куда ${ Displaystyle му = Г (М + м)}$ это гравитационный параметр с ${ displaystyle M}$ и ${ displaystyle m}$ в массы центрального тела и возмущенного тела, ${ Displaystyle mathbf {а} _ { текст {пер}}}$ возмущает ускорение, и ${ displaystyle r}$ и ${ displaystyle rho}$ величины ${ displaystyle mathbf {r}}$ и ${ displaystyle { boldsymbol { rho}}}$.

Подставляя из уравнений (3) и (4) в уравнение (2),

${ displaystyle { ddot { delta mathbf {r}}} = mathbf {a} _ { text {per}} + mu left ({{ boldsymbol { rho}} over rho ^ {3}} - { mathbf {r} over r ^ {3}} right),}$

(5)

которые теоретически можно проинтегрировать дважды, чтобы найти ${ displaystyle delta mathbf {r}}$. Поскольку соприкасающаяся орбита легко вычисляется двухчастичными методами, ${ displaystyle { boldsymbol { rho}}}$ и ${ displaystyle delta mathbf {r}}$ учитываются и ${ displaystyle mathbf {r}}$ можно решить. На практике количество в скобках, ${ displaystyle {{ boldsymbol { rho}} over rho ^ {3}} - { mathbf {r} over r ^ {3}}}$, представляет собой разность двух почти равных векторов, и необходимы дальнейшие манипуляции, чтобы избежать необходимости в дополнительных значащие цифры.^[8][9]

Метод Сперлинга – Бурде

В 1991 году Виктор Р. Бонд и Майкл Фрайетта создали эффективный и высокоточный метод решения проблемы возмущения двух тел.^[10] В этом методе используются линеаризованные и регуляризованные дифференциальные уравнения движения, выведенные Гансом Сперлингом, и теория возмущений, основанная на этих уравнениях, разработанная К.А. Бурде в 1864 году. В 1973 году Бонд и Хансен улучшили систему дифференциальных уравнений Бурде, используя в качестве параметра полную энергию возмущенной системы вместо энергии двух тел и уменьшив количество элементов до 13. В 1989 году Бонд и Готлиб встроил интеграл Якоби, который является константой, когда потенциальная функция явно зависит от времени, а также от положения в уравнениях Ньютона. Постоянная Якобиана использовалась как элемент для замены полной энергии в переформулировке дифференциальных уравнений движения. В этом процессе вводится другой элемент, который пропорционален составляющей углового момента. В результате общее количество элементов вернулось к 14. В 1991 году Бонд и Фрайетта внесли дополнительные изменения, заменив вектор Лапласа другим векторным интегралом, а также другим скалярным интегралом, который удалил небольшие вековые члены, которые появлялись в дифференциальных уравнениях для некоторых из них. элементы.^[11]

Метод Сперлинга – Бёрдета состоит из 5 этапов, а именно:^[11]

Шаг 1: Инициализация

Учитывая исходное положение, ${ displaystyle mathbf {r} _ {0}}$, начальная скорость, ${ displaystyle mathbf {v} _ {0}}$, и начальное время, ${ displaystyle t_ {0}}$, инициализируются следующие переменные:

${ displaystyle s = 0}$

${ displaystyle r_ {0} = ( mathbf {r} _ {0} cdot mathbf {r} _ {0}) ^ {1/2}}$

${ displaystyle a = r_ {0}}$

${ displaystyle b = mathbf {r} _ {0} cdot mathbf {v} _ {0}}$

${ Displaystyle тау = т_ {0}}$

${ displaystyle { boldsymbol { alpha}} = mathbf {r} _ {0}}$

${ displaystyle { boldsymbol { beta}} = а mathbf {v} _ {0}}$

Возмущения из-за возмущающих масс, определяемых как ${ displaystyle V_ {0}}$ и ${ displaystyle { Bigg [} { partial {V} over { partial { mathbf {r}}}} { Bigg]} _ {0}}$, оцениваются

Возмущения из-за других ускорений, определяемых как ${ displaystyle mathbf {P} _ {0}}$, оцениваются

${ displaystyle alpha _ {J} = { frac {2 mu} {r_ {0}}} - mathbf {v} _ {0} cdot mathbf {v} _ {0} -2V_ {0 }}$

${ displaystyle gamma = mu - alpha _ {J} a}$

${ displaystyle { boldsymbol { delta}} = - ( mathbf {v} _ {0} cdot mathbf {v} _ {0}) mathbf {r} _ {0} + ( mathbf {r } _ {0} cdot mathbf {v} _ {0}) mathbf {v} _ {0} + { frac { mu} {r_ {0}}} mathbf {r} _ {0} - alpha _ {J} mathbf {r} _ {0}}$

${ displaystyle sigma = 0}$

Шаг 2. Преобразуйте элементы в координаты

${ displaystyle mathbf {r} = { boldsymbol { alpha}} + { boldsymbol { beta}} sc_ {1} + { boldsymbol { delta}} s ^ {2} c_ {2}}$

${ displaystyle mathbf {r '} = { boldsymbol { beta}} c_ {0} + { boldsymbol { delta}} sc_ {1}}$

${ displaystyle mathbf {x} _ {3} = alpha _ {J} ({ boldsymbol { alpha}} - mathbf {r}) + { boldsymbol { delta}}}$

${ displaystyle gamma = mu - alpha _ {J} a}$

${ displaystyle r = a + bsc_ {1} + gamma s ^ {2} c_ {2}}$

${ Displaystyle mathbf {v} = mathbf {r '} / r}$

${ displaystyle r '= bc_ {0} + gamma sc_ {1}}$

${ displaystyle t = tau + as + bs ^ {2} c_ {2} + gamma s ^ {3} c_ {3}}$

куда ${ displaystyle c_ {0}, c_ {1}, c_ {2}, c_ {3}}$ находятся Функции Stumpff

Шаг 3. Оцените дифференциальные уравнения для элементов.

${ displaystyle mathbf {F} = mathbf {P} - { partial {V} over partial { mathbf {r}}}}$

${ Displaystyle mathbf {Q} = г ^ {2} mathbf {F} +2 mathbf {r} (-V + sigma)}$

${ displaystyle alpha '_ {J} = 2 (- mathbf {r'} + r { boldsymbol { omega}} times mathbf {r}) cdot mathbf {P}}$

${ displaystyle mu { boldsymbol { epsilon}} '= 2 ( mathbf {r'} cdot mathbf {F}) mathbf {r} - ( mathbf {r} cdot mathbf {F} ) mathbf {r '} - ( mathbf {r} cdot mathbf {r'}) mathbf {F}}$

${ displaystyle { boldsymbol { alpha}} '= - mathbf {Q} sc_ {1} - mu { boldsymbol { epsilon}}' s ^ {2} c_ {2} - alpha '_ { J} { big [} { boldsymbol { alpha}} s ^ {2} c_ {2} +2 { boldsymbol { beta}} s ^ {3} { bar {c}} _ {3} + { frac {1} {2}} { boldsymbol { delta}} s ^ {4} c_ {2} ^ {2} { big]}}$

${ displaystyle { boldsymbol { beta}} '= mathbf {Q} c_ {0} + mu { boldsymbol { epsilon}}' sc_ {1} + alpha '_ {J} { big [ } { boldsymbol { alpha}} sc_ {1} + { boldsymbol { beta}} s ^ {2} { bar {c}} _ {2} - { boldsymbol { delta}} s ^ { 3} (2 { bar {c}} _ {3} -c_ {1} c_ {2}) { big]}}$

${ displaystyle { boldsymbol { delta}} '= mathbf {Q} alpha _ {J} sc_ {1} - mu { boldsymbol { epsilon}}' c_ {0} + alpha '_ { J} { big [} - { boldsymbol { alpha}} c_ {0} +2 alpha _ {J} { boldsymbol { beta}} s ^ {3} { bar {c}} _ { 3} + { frac {1} {2}} { boldsymbol { delta}} alpha _ {J} s ^ {4} c_ {2} ^ {2} { big]}}$

${ displaystyle sigma '= r { boldsymbol { omega}} cdot mathbf {r} times mathbf {F}}$

${ displaystyle a '= - { frac {1} {r}} mathbf {r} cdot mathbf {Q} sc_ {1} - alpha _ {J}' { big [} as ^ {2 } c_ {2} + 2bs ^ {3} { bar {c}} _ {3} + { frac {1} {2}} gamma s ^ {4} c_ {2} ^ {2} { большой ]}}$

${ displaystyle b '= { frac {1} {r}} mathbf {r} cdot mathbf {Q} c_ {0} + alpha _ {J}' { big [} asc_ {1} + bs ^ {2} { bar {c}} _ {2} - gamma s ^ {3} (2 { bar {c}} _ {3} -c_ {1} c_ {2}) { big ]}}$

${ displaystyle gamma '= - { frac {1} {r}} mathbf {r} cdot mathbf {Q} alpha _ {J} sc_ {1} + alpha _ {J}' { большой [} -ac_ {0} + 2b alpha _ {J} s ^ {3} { bar {c}} _ {3} + { frac {1} {2}} gamma alpha _ {J } s ^ {4} c_ {2} ^ {2} { big]}}$

${ displaystyle tau '= { frac {1} {r}} mathbf {r} cdot mathbf {Q} s ^ {2} c_ {2} + alpha _ {J}' { big [ } как ^ {3} c_ {3} + { frac {1} {2}} bs ^ {4} c_ {2} ^ {2} -2 gamma s ^ {5} (c_ {5} -4 { bar {c}} _ {5}) { big]}}$

Шаг 4: интеграция

Здесь дифференциальные уравнения интегрируются за период ${ displaystyle Delta s}$ чтобы получить значение элемента в ${ displaystyle s + Delta s}$

Шаг 5: продвижение

Набор ${ displaystyle s = s + Delta s}$ и вернитесь к шагу 2, пока не будут выполнены условия остановки моделирования.

Модели возмущающих сил

Возмущающие силы вызывают возмущение орбит от идеальной кеплеровской орбиты. Модели для каждой из этих сил создаются и выполняются во время моделирования орбиты, поэтому можно определить их влияние на орбиту.

Несферическая гравитация

Земля не является идеальной сферой, и масса не распределена равномерно внутри Земли. Это приводит к тому, что модель гравитации точечной массы неточна для орбит вокруг Земли, особенно Низкие околоземные орбиты. Чтобы учесть вариации гравитационного потенциала вокруг поверхности Земли, гравитационное поле Земли моделируется с помощью сферических гармоник.^[12] которые выражаются уравнением:

${ displaystyle { mathbf {f}} = - { frac { mu} {R ^ {2}}} mathbf { hat {r}} + sum _ {n = 2} ^ { infty} sum _ {m = 0} ^ {n} { mathbf {f}} _ {n, m}}$

куда

${ displaystyle { mu}}$ - гравитационный параметр, определяемый как произведение G, универсальная гравитационная постоянная, и масса основного тела.

${ displaystyle mathbf { hat {r}}}$ - единичный вектор, определяющий расстояние между первичным и вторичным телами, с ${ displaystyle {R}}$ величина расстояния.

${ displaystyle { mathbf {f}} _ {n, m}}$ представляет собой вклад в ${ displaystyle { mathbf {f}}}$ сферической гармоники степени п и заказать м, который определяется как:^[12]

${ displaystyle { begin {align} mathbf {f} _ {n, m} & = { frac { mu R_ {O} ^ {2}} {R ^ {n + m + 1}}} left ({ frac {C_ {n, m} { mathcal {C}} _ ​​{m} + S_ {n, m} { mathcal {S}} _ {m}} {R}} (A_ {n , m + 1} mathbf { hat {e}} _ {3} - left (s _ { lambda} A_ {n, m + 1} + (n + m + 1) A_ {n, m} right) mathbf { hat {r}} right) [10pt] & {} quad {} + mA_ {n, m} ((C_ {n, m} { mathcal {C}} _ ​​{ m-1} + S_ {n, m} { mathcal {S}} _ {m-1}) mathbf { hat {e}} _ {1} + (S_ {n, m} { mathcal { C}} _ ​​{m-1} -C_ {n, m} { mathcal {S}} _ {m-1}) mathbf { hat {e}} _ {2})) end {выровнено} }}$

куда:

${ displaystyle R_ {O}}$ - средний экваториальный радиус основного тела.

${ displaystyle R}$ - величина вектора положения от центра первичного тела к центру вторичного тела.

${ displaystyle C_ {n, m}}$ и ${ displaystyle S_ {n, m}}$ гравитационные коэффициенты степени п и заказать м. Обычно их можно найти через гравиметрия измерения.

Единичные векторы ${ displaystyle mathbf { hat {e}} _ {1}, mathbf { hat {e}} _ {2}, mathbf { hat {e}} _ {3}}$ определить систему координат, закрепленную на основном теле. Для Земли, ${ displaystyle mathbf { hat {e}} _ {1}}$ лежит в экваториальной плоскости параллельно линии, пересекающей геометрический центр Земли и Гринвичский меридиан,${ displaystyle mathbf { hat {e}} _ {3}}$ указывает в направлении северной полярной оси, и ${ displaystyle mathbf { hat {e}} _ {2} = mathbf { hat {e}} _ {3} times mathbf { hat {e}} _ {1}}$

${ displaystyle A_ {n, m}}$ называется производным Полином Лежандра степени п и заказать м. Они решаются через отношение повторения: ${ Displaystyle A_ {n, m} (u) = { frac {1} {nm}} ((2n-1) uA_ {n-1, m} (u) - (n + m-1) A_ { п-2, м} (и))}$

${ displaystyle s _ { lambda}}$ является синусом географической широты вторичного тела, который ${ displaystyle mathbf { hat {r}} cdot mathbf { hat {e}} _ {3}}$.

${ displaystyle { mathcal {C}} _ ​​{m}, { mathcal {S}} _ {m}}$ определяются следующим рекуррентным соотношением и начальными условиями:${ displaystyle { mathcal {C}} _ ​​{m} = { mathcal {C}} _ ​​{1} { mathcal {C}} _ ​​{m-1} - { mathcal {S}} _ {1 } { mathcal {S}} _ {m-1}, { mathcal {S}} _ {m} = { mathcal {S}} _ {1} { mathcal {C}} _ ​​{m-1 } + { mathcal {C}} _ ​​{1} { mathcal {S}} _ {m-1}, { mathcal {S}} _ {0} = 0, { mathcal {S}} _ { 1} = mathbf {R} cdot mathbf { hat {e}} _ {2}, { mathcal {C}} _ ​​{0} = 1, { mathcal {C}} _ ​​{1} = mathbf {R} cdot mathbf { hat {e}} _ {1}}$

При моделировании возмущений орбиты вокруг первичного тела только сумма ${ displaystyle { mathbf {f}} _ {n, m}}$ члены должны быть включены в возмущение, поскольку модель точечной гравитации учитывается в ${ displaystyle - { frac { mu} {R ^ {2}}} mathbf { hat {r}}}$ срок

Возмущения третьего тела

Гравитационные силы от третьих тел могут вызывать возмущения орбиты. Например, солнце и Луна вызывают возмущения на орбитах вокруг Земли.^[13] Эти силы моделируются так же, как гравитация для первичного тела с помощью Прямое гравитационное моделирование N-тел. Обычно для моделирования эффектов от этих третьих тел используется только сферическая модель гравитации точечной массы.^[14]Некоторые частные случаи возмущений третьего тела имеют приближенные аналитические решения. Например, возмущения для прямого восхождения восходящего узла и аргумента перигея для круговой околоземной орбиты:^[13]

${ displaystyle { dot { Omega}} _ { mathrm {MOON}} = - 0,00338 ( cos (i)) / n}$

${ displaystyle { dot { omega}} _ { mathrm {MOON}} = - 0,00169 (4-5 sin ^ {2} (i)) / n}$

куда:

${ displaystyle { dot { Omega}}}$ изменение направления восхождения восходящего узла в градусах за день.

${ displaystyle { dot { omega}}}$ - изменение аргумента перигея в градусах за день.

${ displaystyle i}$ наклонение орбиты.

${ displaystyle n}$ - количество орбитальных оборотов в сутки.

Солнечная радиация

Давление солнечной радиации вызывает возмущения орбиты. Величина ускорения, которое он передает космическому аппарату на околоземной орбите, моделируется с помощью следующего уравнения:^[13]

${ displaystyle a_ {R} приблизительно -4,5 times 10 ^ {- 6} (1 + r) A / m}$

куда:

${ displaystyle a_ {R}}$ - величина ускорения в метрах на секунду в квадрате.

${ displaystyle A}$ это площадь поперечного сечения, подверженная воздействию солнце в квадратных метрах.

${ displaystyle m}$ масса КА в килограммы.

${ displaystyle r}$ коэффициент отражения, зависящий от свойств материала. ${ displaystyle r = 0}$ для абсорбции, ${ displaystyle r = 1}$ для зеркального отражения и ${ displaystyle r приблизительно 0,4}$ для диффузного отражения.

Для орбит вокруг Земли давление солнечной радиации становится более сильной силой, чем сопротивление на высоте более 800 км.^[13]

Движение

Есть много разных типов двигателей космических кораблей. Ракетные двигатели - одни из самых широко используемых. Сила ракетного двигателя моделируется уравнением:^[15]

${ displaystyle F_ {n} = { dot {m}} ; v _ { text {e}} = { dot {m}} ; v _ { text {e-act}} + A _ { text {e}} (p _ { text {e}} - p _ { text {amb}})}$

куда:
${ displaystyle { dot {m}}}$	= массовый расход выхлопных газов
${ displaystyle v _ { text {e}}}$	= эффективная скорость выхлопа
${ displaystyle v _ { text {e-act}}}$	= фактическая скорость струи в выходной плоскости сопла
${ displaystyle A _ { text {e}}}$	= проходное сечение в выходной плоскости сопла (или плоскости, в которой струя выходит из сопла при отрывном потоке)
${ displaystyle p _ { text {e}}}$	= статическое давление в выходной плоскости сопла
${ displaystyle p _ { text {amb}}}$	= окружающее (или атмосферное) давление

Другой возможный метод - это солнечный парус. Использование солнечных парусов радиационное давление таким образом, чтобы достичь желаемой движущей силы.^[16] Модель возмущения, вызванного солнечным ветром, может использоваться как модель движущей силы солнечного паруса.

Тащить

Основная негравитационная сила, действующая на спутники на низкой околоземной орбите, - это сопротивление атмосферы.^[13] Перетаскивание будет действовать против направления скорости и снимать энергию с орбиты. Сила от сопротивления моделируется следующим уравнением:

${ Displaystyle F_ {D} , = , { tfrac {1} {2}} , rho , v ^ {2} , C_ {d} , A,}$

куда

${ displaystyle mathbf {F} _ {D}}$ это сила сопротивления,

${ Displaystyle mathbf {} rho}$ это плотность жидкости,^[17]

${ displaystyle mathbf {} v}$ это скорость объекта относительно жидкости,

${ displaystyle mathbf {} C_ {d}}$ это коэффициент трения (а безразмерный параметр, например От 2 до 4 для большинства спутников^[13])

${ displaystyle mathbf {} A}$ это ссылка площадь.

Орбиты с высотой ниже 120 км обычно имеют такое большое сопротивление, что орбиты затухают слишком быстро, чтобы обеспечить спутнику достаточный срок службы для выполнения любой практической миссии. С другой стороны, орбиты с высотой более 600 км имеют относительно небольшое сопротивление, так что орбита затухает достаточно медленно, чтобы не оказывать реального воздействия на спутник в течение его срока службы.^[13] Плотность воздуха может существенно различаться в термосфера где находится большинство спутников на низкой околоземной орбите. Изменение происходит в первую очередь из-за солнечной активности, и поэтому солнечная активность может сильно влиять на силу сопротивления космического корабля и усложнять долгосрочное моделирование орбиты.^[13]

Магнитные поля

Магнитные поля могут играть значительную роль в качестве источника возмущения орбиты, как было показано на Объект длительного воздействия.^[12] Как и гравитация, магнитное поле Земли можно выразить через сферические гармоники, как показано ниже:^[12]

${ displaystyle { mathbf {B}} = sum _ {n = 1} ^ { infty} sum _ {m = 0} ^ {n} { mathbf {B}} _ {n, m}}$

куда

${ displaystyle { mathbf {B}}}$ - вектор магнитного поля в точке над поверхностью Земли.

${ displaystyle { mathbf {B}} _ {n, m}}$ представляет собой вклад в ${ displaystyle { mathbf {B}}}$ сферической гармоники степени п и заказать м, определяется как:^[12]

${ displaystyle { begin {align} mathbf {B} _ {n, m} = {} & { frac {K_ {n, m} a ^ {n + 2}} {R ^ {n + m + 1}}} left [{ frac {g_ {n, m} { mathcal {C}} _ ​​{m} + h_ {n, m} { mathcal {S}} _ {m}} {R} } ((s _ { lambda} A_ {n, m + 1} + (n + m + 1) A_ {n, m}) mathbf { hat {r}}) -A_ {n, m + 1} mathbf { hat {e}} _ {3} right] [10pt] & {} - mA_ {n, m} ((g_ {n, m} { mathcal {C}} _ ​​{m- 1} + h_ {n, m} { mathcal {S}} _ {m-1}) mathbf { hat {e}} _ {1} + (h_ {n, m} { mathcal {C} } _ {m-1} -g_ {n, m} { mathcal {S}} _ {m-1}) mathbf { hat {e}} _ {2})) end {align}}}$

куда:

${ displaystyle a}$ - средний экваториальный радиус основного тела.

${ displaystyle R}$ - величина вектора положения от центра первичного тела к центру вторичного тела.

${ displaystyle mathbf { hat {r}}}$ - единичный вектор в направлении вторичного тела с центром в центре первичного тела.

${ displaystyle g_ {n, m}}$ и ${ displaystyle h_ {n, m}}$ - коэффициенты Гаусса степени п и заказать м. Обычно их можно найти через магнитное поле измерения.

Единичные векторы ${ displaystyle mathbf { hat {e}} _ {1}, mathbf { hat {e}} _ {2}, mathbf { hat {e}} _ {3}}$ определить систему координат, закрепленную на основном теле. Для Земли, ${ displaystyle mathbf { hat {e}} _ {1}}$ лежит в экваториальной плоскости параллельно линии, пересекающей геометрический центр Земли и Гринвичский меридиан,${ displaystyle mathbf { hat {e}} _ {3}}$ указывает в направлении северной полярной оси, и ${ Displaystyle mathbf { hat {e}} _ {2} = mathbf { hat {e}} _ {3} times mathbf { hat {e}} _ {1}}$

${ displaystyle A_ {n, m}}$ называется производным Полином Лежандра степени п и заказать м. Они решаются через рекуррентное соотношение: ${ Displaystyle A_ {n, m} (u) = { frac {1} {nm}} ((2n-1) uA_ {n-1, m} (u) - (n + m-1) A_ { п-2, м} (и))}$

${ displaystyle K_ {n, m}}$ определяется как: 1, если м = 0, ${ displaystyle { big [} { frac {n-m} {n + m}} { big]} ^ {0,5} K_ {n-1, m}}$ за ${ Displaystyle п geq (м + 1)}$ и ${ Displaystyle м = [1 ldots infty]}$ , и ${ Displaystyle [(п + м) (п-м + 1)] ^ {- 0,5} К_ {п, м-1}}$ за ${ displaystyle n geq m}$ и ${ Displaystyle м = [2 ldots infty]}$

${ displaystyle s _ { lambda}}$ является синусом географической широты вторичного тела, который ${ displaystyle mathbf { hat {r}} cdot mathbf { hat {e}} _ {3}}$.

${ displaystyle { mathcal {C}} _ ​​{m}, { mathcal {S}} _ {m}}$ определяются следующим рекуррентным соотношением и начальными условиями:${ displaystyle { mathcal {C}} _ ​​{m} = { mathcal {C}} _ ​​{1} { mathcal {C}} _ ​​{m-1} - { mathcal {S}} _ {1 } { mathcal {S}} _ {m-1}, { mathcal {S}} _ {m} = { mathcal {S}} _ {1} { mathcal {C}} _ ​​{m-1 } + { mathcal {C}} _ ​​{1} { mathcal {S}} _ {m-1}, { mathcal {S}} _ {0} = 0, { mathcal {S}} _ { 1} = mathbf {R} cdot mathbf { hat {e}} _ {2}, { mathcal {C}} _ ​​{0} = 1, { mathcal {C}} _ ​​{1} = mathbf {R} cdot mathbf { hat {e}} _ {1}}$

Смотрите также

• проблема н-тела
• Орбитальный резонанс
• Оскулирующая орбита
• Возмущение (астрономия)
• Сфера влияния (астродинамика)
• Проблема двух тел

Примечания и ссылки

внешняя ссылка

• [1] Карты гравитации Земли