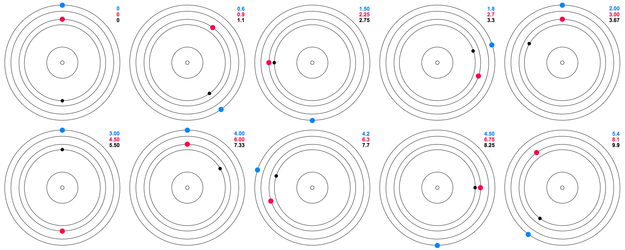
Орбитальный резонанс - Orbital resonance

Для научно-фантастического романа см. Орбитальный резонанс (роман).

Трехчастичный резонанс Лапласа демонстрируют три звезды Юпитера. Галилеевы луны. Союзы выделяются краткими изменениями цвета. Есть два соединения Ио-Европа (зеленый) и три соединения Ио-Ганимед (серый) для каждого соединения Европа-Ганимед (пурпурный). Диаграмма не в масштабе.

В небесная механика, орбитальный резонанс происходит когда вращающийся по орбите тела проявляют регулярные, периодические гравитационный влияют друг на друга, обычно потому, что их орбитальные периоды связаны соотношением малых целые числа. Чаще всего это отношение обнаруживается для пары объектов. Физический принцип, лежащий в основе орбитального резонанса, аналогичен по концепции толканию ребенка на качать, где и орбита, и качание имеют собственная частота, а другое тело, выполняющее «толчок», будет действовать периодически, чтобы иметь кумулятивный эффект на движение. Орбитальные резонансы значительно усиливают взаимное гравитационное влияние тел (т.е., их способность изменять или ограничивать орбиты друг друга). В большинстве случаев это приводит к неустойчивый взаимодействие, при котором тела обмениваются импульс и сместить орбиты до тех пор, пока резонанс не исчезнет При некоторых обстоятельствах резонансная система может быть самокорректирующейся и, следовательно, стабильной. Примеры: резонанс 1: 2: 4 Юпитер луны Ганимед, Европа и Ио, и резонанс 2: 3 между Плутон и Нептун. Неустойчивые резонансы с Сатурн внутренние луны порождают пробелы в кольца Сатурна. Частный случай резонанса 1: 1 между телами с одинаковыми радиусами орбиты вызывает большие Солнечная система тела для изгнания большинства других тел, разделяющих их орбиты; это часть гораздо более обширного процесса очистка окрестностей, эффект, который используется в текущем определение планеты.[1]

Коэффициент бинарного резонанса в этой статье следует интерпретировать как соотношение количества орбит завершено в тот же интервал времени, а не как соотношение орбитальных периодов, что было бы обратным соотношением. Таким образом, соотношение 2: 3, приведенное выше, означает, что Плутон совершает два обращения за время, необходимое Нептуну для завершения трех. В случае резонансных соотношений между тремя или более телами может использоваться любой тип отношения (в таких случаях последовательности наименьших целочисленных соотношений не обязательно являются инверсиями друг друга), и тип отношения будет указан.

История

С момента открытия Закон всемирного тяготения Ньютона в 17 веке стабильность Солнечной системы занимал многих математиков, начиная с Пьер-Симон Лаплас. Устойчивые орбиты, возникающие в двухчастичное приближение игнорировать влияние других тел. Влияние этих дополнительных взаимодействий на стабильность Солнечная система очень мало, но сначала не было известно, могут ли они складываться в течение более длительных периодов, чтобы значительно изменить параметры орбиты и привести к совершенно другой конфигурации, или же некоторые другие стабилизирующие эффекты могут поддерживать конфигурацию орбит планет.

Именно Лаплас нашел первые ответы, объясняющие взаимосвязь орбит Галилеевы луны (Смотри ниже). До Ньютона также учитывались соотношения и пропорции в орбитальных движениях, в том, что называлось «музыкой сфер» или musica universalis.

Статья о резонансные взаимодействия описывает резонанс в общей современной обстановке. Первичный результат изучения динамические системы открытие и описание очень упрощенной модели синхронизации мод; это осциллятор, который периодически получает толчки через слабую связь с каким-либо приводным двигателем. Аналогом здесь может быть то, что более массивное тело обеспечивает периодический гравитационный толчок меньшему телу, когда оно проходит мимо. Области с синхронизацией мод названы Языки Арнольда.

Виды резонанса

В большие полуоси из резонансные транснептуновые объекты (красный) сгруппированы в местах низкоцелочисленных резонансов с Нептун (вертикальные красные полосы вверху), в отличие от Cubewanos (синий) и нерезонансный (или заведомо не резонансный) разбросанные предметы (серый).
График распределения астероид большие полуоси, показывающие Пробелы Кирквуда где орбиты дестабилизированы резонансами с Юпитер
Спиральные волны плотности в Кольцо Сатурна возбуждены резонансами с внутренние луны. Такие волны распространяются от планеты (в сторону верхнего левого угла). Большой набор волн чуть ниже центра вызван резонансом 6: 5 с Янус.
Эксцентричный Кольцо Титана[2] в промежутке Коломбо Сатурна C кольцо (в центре) и наклонные орбиты резонансных частиц в изгибной волне[3][4] просто внутри есть апсидный и узловой прецессии соответственно соизмеримы с Титан подлое движение.

В общем, орбитальный резонанс может

  • включают один или любую комбинацию параметров орбиты (например, эксцентриситет против большая полуось, или эксцентриситет против склонность ).
  • действовать в любом временном масштабе от краткосрочных, соизмеримых с периодами орбиты, до светский, измеряется в 104 до 106 годы.
  • привести либо к долговременной стабилизации орбит, либо стать причиной их дестабилизации.

А орбитальный резонанс среднего движения возникает, когда у двух тел есть периоды революция которые представляют собой простое целочисленное отношение друг к другу. В зависимости от деталей это может стабилизировать или дестабилизировать орбиту.Стабилизация может произойти, когда два тела движутся так синхронно, что никогда не сближаются. Например:

  • Орбиты Плутон и Plutinos стабильны, несмотря на пересечение более крупных Нептун, потому что они находятся в резонансе 2: 3. Резонанс гарантирует, что, когда они приближаются к перигелию и орбите Нептуна, Нептун постоянно находится далеко (в среднем четверть своей орбиты). Другие (гораздо более многочисленные) пересекающие Нептун тела, не находящиеся в резонансе, были выброшены из этой области сильным возмущения из-за Нептуна. Есть также небольшие, но значительные группы резонансные транснептуновые объекты занимая 1: 1 (Нептун трояны ), 3:5, 4:7, 1:2 (двое ) и 2:5 резонансы, среди прочего, по отношению к Нептуну.
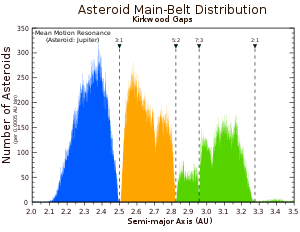
  • в пояс астероидов за пределами 3,5 а.е. от Солнца, 3: 2, 4: 3 и 1: 1 резонируют с Юпитер населены комки астероидов ( Семья Хильды, несколько Астероиды туле, и многочисленные Троянские астероиды, соответственно).

Орбитальные резонансы также могут дестабилизировать одна из орбит. Этот процесс можно использовать для поиска энергоэффективных способов спуск с орбиты космический корабль.[5][6] Для небольших тел дестабилизация гораздо более вероятна. Например:

  • в пояс астероидов в пределах 3,5 а.е. от Солнца основные резонансы среднего движения с Юпитер являются местоположениями пробелы в распределении астероидов Пробелы Кирквуда (особенно при резонансах 4: 1, 3: 1, 5: 2, 7: 3 и 2: 1). Астероиды были выброшены с этих почти пустых переулков из-за неоднократных возмущений. Однако в этих резонансах или вблизи них все еще есть популяции астероидов. Например, астероиды Семья Алинда находятся в резонансе 3: 1 или близки к нему, причем их орбитальный эксцентриситет постоянно увеличивается за счет взаимодействий с Юпитером, пока они в конечном итоге не встретятся с внутренней планетой, которая выталкивает их из резонанса.
  • в кольца Сатурна, то Кассини Дивизион это разрыв между внутренним Приносить и внешний Кольцо который был очищен резонансом 2: 1 с луной Мимас. (Точнее, местом резонанса является Гюйгенс Гэп, ограничивающий внешний край Приносить.)
  • В кольцах Сатурна Энке и Киллер зазоры внутри кольца A очищаются резонансами 1: 1 со встроенными лунками Сковорода и Дафнис, соответственно. Внешний край кольца А поддерживается дестабилизирующим резонансом 7: 6 с луной. Янус.

Большинство тел находятся на резонансной орбите в одном направлении; Тем не менее ретроградный астероид 514107 Kaʻepaokaʻawela похоже, находится в стабильном (в течение как минимум миллиона лет) резонансе 1: -1 с Юпитером.[7] Кроме того, несколько ретроградных дамоклоиды были обнаружены, которые временно захватываются в резонансе среднего движения с Юпитер или же Сатурн.[8] Такие орбитальные взаимодействия слабее, чем соответствующие взаимодействия между телами, вращающимися в одном направлении.[8]

А Лапласовский резонанс представляет собой трехчастичный резонанс с соотношением орбитальных периодов 1: 2: 4 (эквивалентно соотношению орбит 4: 2: 1). Термин возник потому, что Пьер-Симон Лаплас обнаружил, что такой резонанс управляет движениями спутников Юпитера. Ио, Европа, и Ганимед. Теперь он также часто применяется к другим 3-частным резонансам с такими же отношениями,[9] например, между внесолнечные планеты Gliese 876 c, b и e.[10][11] Трехчастичные резонансы, включающие другие простые целочисленные отношения, были названы «подобными Лапласу».[12] или «типа Лапласа».[13]

А Линдблад резонанс диски спиральные волны плотности оба в галактики (где звезды подвержены принуждение самими спиральными рукавами) и в Кольца Сатурна (где кольцевые частицы подвергаются воздействию Спутники Сатурна ).

А светский резонанс происходит, когда прецессия двух орбит синхронизируется (обычно прецессия перигелий или же восходящий узел ). Маленькое тело в вековом резонансе с гораздо большим (например, планета ) будет прецессировать с той же скоростью, что и большое тело. Через долгое время (миллион лет или около того) вековой резонанс изменит эксцентриситет и склонность маленького тела.

Несколько ярких примеров секулярного резонанса связаны с Сатурном. Резонанс между прецессией оси вращения Сатурна и прецессией орбитальной оси Нептуна (оба из которых имеют периоды около 1,87 миллиона лет) был идентифицирован как вероятный источник большой осевой наклон (26.7°).[14][15][16] Изначально Сатурн, вероятно, имел наклон ближе к Юпитеру (3,1 °). Постепенное истощение пояса Койпера уменьшило бы скорость прецессии орбиты Нептуна; в конечном итоге частоты совпали, и осевая прецессия Сатурна была захвачена в спин-орбитальный резонанс, что привело к увеличению угла наклона Сатурна. (Угловой момент орбиты Нептуна равен 104 раз больше скорости вращения Сатурна, и поэтому доминирует над взаимодействием.)

В вековой резонанс перигелия между астероиды и Сатурн (ν6 = грамм − грамм6) помогает формировать пояс астероидов (индекс «6» обозначает Сатурн как шестую планету от Солнца). Астероиды, которые приближаются к нему, постепенно увеличивают эксцентриситет, пока не станут Пересекающие Марс, в этот момент они обычно выбрасываются из пояс астероидов рядом с Марс. Этот резонанс образует внутреннюю и «боковую» границы пояс астероидов около 2 Австралия, и при наклонах около 20 °.

Численное моделирование показало, что возможное образование векового резонанса перигелия между Меркурий и Юпитер (грамм1 = грамм5) может значительно увеличить эксцентриситет Меркурия и, возможно, дестабилизировать внутреннюю часть Солнечной системы через несколько миллиардов лет.[17][18]

В Кольцо Титана в пределах Сатурна C кольцо представляет собой другой тип резонанса, в котором скорость апсидальная прецессия одной орбиты точно соответствует скорости вращения другой. Внешний конец этого эксцентрического колечка всегда указывает на большую луну Сатурна. Титан.[2]

А Козай резонанс возникает, когда наклон и эксцентриситет возмущенный орбиты колеблются синхронно (увеличивая эксцентриситет при уменьшении наклона и наоборот). Этот резонанс применим только к телам на сильно наклоненных орбитах; как следствие, такие орбиты имеют тенденцию быть нестабильными, поскольку растущий эксцентриситет приведет к небольшому перицентры, обычно приводящие к столкновению или (для больших лун) разрушению приливные силы.

В примере другого типа резонанса, включающего эксцентриситет орбиты, эксцентриситеты Ганимеда и Каллисто изменяются с общим периодом 181 год, хотя и с противоположными фазами.[19]

Резонансы среднего движения в Солнечной системе

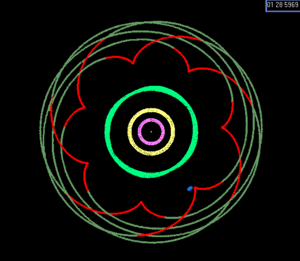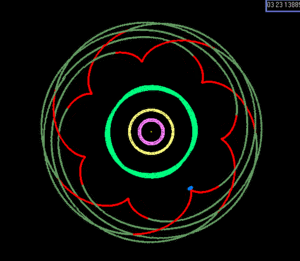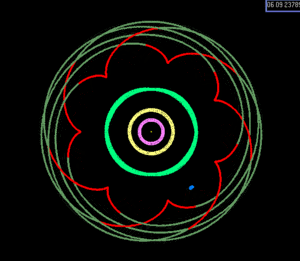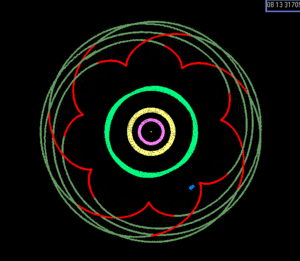
Изображение Хаумеа предполагаемый резонанс 7:12 с Нептун в вращающаяся рама, с Нептуном (синяя точка в правом нижнем углу) неподвижным. Смещение орбиты Хаумеа относительно Нептуна периодически меняет местами (либрирует ), сохраняя резонанс.

Известно лишь несколько резонансов среднего движения в Солнечная система с участием планет, карликовые планеты или больше спутники (гораздо большее число включает астероиды, планетарные кольца, луны и меньше Пояс Койпера объекты, в том числе многие возможные карликовые планеты ).

Кроме того, Хаумеа считается, что он находится в резонансе 7:12 с Нептуном,[20][21] и 225088 Гонггун считается, что он находится в резонансе 3:10 с Нептуном.[22]

Простые целочисленные отношения между периодами скрывают более сложные отношения:

В качестве иллюстрации последнего рассмотрим хорошо известный резонанс Ио-Европы 2: 1. Если бы периоды обращения были в этом отношении, то средние движения (инверсия периодов, часто выражаемая в градусах в день) удовлетворяла бы следующему

Подставляя данные (из Википедии), получим −0,7395 ° день.−1, значение, существенно отличное от нуля.

Собственно, резонанс является совершенный, но он включает также прецессию Perijove (точка, ближайшая к Юпитеру), . Правильное уравнение (часть уравнений Лапласа):

Другими словами, среднее движение Ио действительно вдвое больше, чем у Европы, с учетом прецессии перийова. Наблюдатель, сидящий на (дрейфующем) перийове, увидит, как луны соединяются в одном месте (удлинение). Другие пары, перечисленные выше, удовлетворяют тому же типу уравнения, за исключением резонанса Мимаса-Тетиса. В этом случае резонанс удовлетворяет уравнению

Точка соединения колеблется вокруг середины между узлы двух лун.

Лапласовский резонанс

Иллюстрация резонанса Ио – Европа – Ганимед. От центра наружу: Ио (желтый), Европа (серый) и Ганимед (темный)

Резонанс Лапласа с участием Ио – Европы – Ганимеда включает следующее соотношение, фиксирующее орбитальная фаза лун:

куда находятся средние долготы лун (второй знак равенства игнорирует либрацию).

Это отношение делает тройное соединение невозможным. (Резонанс Лапласа в Gliese 876 система, напротив, связана с одним тройным соединением на орбиту самой удаленной планеты, игнорируя либрацию.) График показывает положения лун после 1, 2 и 3 периодов Ио. либрат около 180 ° с амплитудой 0,03 °.[23]

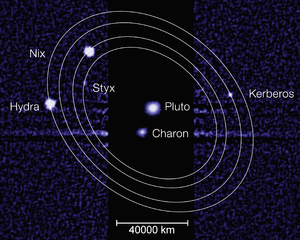
Другой «лапласовский» резонанс связан с луны Стикс, Nix и Гидра Плутона:[12]

Это отражает орбитальные периоды Стикса, Никса и Гидры соответственно, которые близки к соотношению 18:22:33 (или, с точки зрения близких резонансов с периодом Харона, 3 + 3/11: 4: 6; см. ниже ); соответствующее соотношение орбит - 11: 9: 6. Исходя из соотношений синодические периоды, существует 5 соединений Стикса и Гидры и 3 соединения Никса и Гидры на каждые 2 соединения Стикса и Никса.[12][24] Как и в случае резонанса сателлитов Галилея, тройные соединения запрещены. либрирует около 180 ° с амплитудой не менее 10 °.[12]

Последовательность соединений Гидры (синий), Никса (красный) и Стикса (черный) на протяжении одной трети их резонансного цикла. Движение происходит против часовой стрелки, а завершенные орбиты подсчитываются в верхнем правом углу диаграмм (щелкните изображение, чтобы увидеть весь цикл).

Плутино резонансы

Карликовая планета Плутон следует по орбите, запутанной в сети резонансов с Нептун. К резонансам относятся:

  • Резонанс среднего движения 2: 3
  • Резонанс перигелий (либрация около 90 °), сохраняя перигелий выше эклиптика
  • Резонанс долготы перигелия относительно долготы Нептуна

Одним из следствий этих резонансов является то, что при пересечении Плутона орбиты Нептуна сохраняется разделение не менее 30 а.е. Минимальное расстояние между двумя телами в целом составляет 17 а.е., а минимальное расстояние между Плутоном и Уран всего 11 AU[25] (видеть Орбита Плутона подробные объяснения и графики).

Следующее по величине тело в аналогичном 2: 3 резонансе с Нептуном, названное Plutino, - вероятная карликовая планета Оркус. Орбита имеет орбиту, аналогичную по наклонению и эксцентриситету орбите Плутона. Однако их взаимный резонанс с Нептуном заставляет их всегда находиться в противоположных фазах своих орбит; Поэтому Оркус иногда называют «анти-Плутоном».[26]

Изображение резонанса между лунами Нептуна Наяда (чье орбитальное движение показано красным) и Thalassa, в представлении, которое вращается вместе с последним

Наяда: резонанс Thalassa 73:69

Самая сокровенная луна Нептуна, Наяда, находится в резонансе четвертого порядка 73:69 со следующей луной, направленной наружу, Thalassa. Обращаясь вокруг Нептуна, более наклонная Наяда последовательно проходит Талассу дважды сверху, а затем дважды снизу, в цикле, который повторяется каждые ~ 21,5 земных суток. Две луны находятся на расстоянии около 3540 км друг от друга. Хотя их орбитальные радиусы различаются всего на 1850 км, Наяда колеблется на ~ 2800 км выше или ниже орбитальной плоскости Таласса при самом близком сближении. Как обычно, этот резонанс стабилизирует орбиты за счет максимального разделения при соединении, но он необычен для роли, которую играет наклон орбиты в облегчении этого избегания в случае, когда эксцентриситет минимален.[27][28][примечание 1]

Резонансы среднего движения между планетами вне Солнечной системы

Резонансная планетная система из двух планет с соотношением орбит 1: 2

Хотя большинство внесолнечный планетарный в обнаруженных системах не было обнаружено, что планеты находятся в резонансах среднего движения, а в цепочках до пяти резонансных планет[30] и до семи как минимум около резонансных планет[31] были раскрыты. Моделирование показало, что во время формирование планетной системы появлению резонансных цепочек планетарных зародышей способствует наличие первичный газовый диск. Как только этот газ рассеивается, 90–95% этих цепочек должны стать нестабильными, чтобы соответствовать низкой частоте наблюдаемых резонансных цепочек.[32]

  • Как уже упоминалось выше, Gliese 876 e, b и c находятся в резонансе Лапласа с соотношением периодов 4: 2: 1 (124,3, 61,1 и 30,0 дней).[10][33][34] В этом случае, либрат с амплитудой 40 ° ± 13 °, а резонанс подчиняется усредненной по времени зависимости:[10]
  • Кеплер-223 имеет четыре планеты в резонансе с соотношением орбит 8: 6: 4: 3 и соотношением периодов 3: 4: 6: 8 (7,3845, 9,8456, 14,7887 и 19,7257 дней).[35][36][37][38] Это первый подтвержденный орбитальный резонанс с четырьмя телами.[39] Либрации в этой системе таковы, что близкие столкновения между двумя планетами происходят только тогда, когда другие планеты находятся на удаленных частях своих орбит. Расчеты показывают, что эта система резонансов должна была образоваться через планетарная миграция.[38]
  • Кеплер-80 d, e, b, c и g имеют периоды в соотношении ~ 1.000: 1.512: 2.296: 3.100: 4.767 (3.0722, 4.6449, 7.0525, 9.5236 и 14.6456 дней). Однако в системе отсчета, которая вращается вместе с соединениями, это сокращается до отношения периодов 4: 6: 9: 12: 18 (отношение орбиты 9: 6: 4: 3: 2). Соединения d и e, e и b, b и c, а также c и g происходят с относительными интервалами 2: 3: 6: 6 (9,07, 13,61 и 27,21 дня) в схеме, которая повторяется примерно каждые 190,5 дней (семь полных циклов во вращающейся системе отсчета) в инерционной или невращающейся системе отсчета (эквивалентно резонансу с соотношением орбит 62: 41: 27: 20: 13 в невращающейся системе отсчета, потому что соединения циркулируют в направлении, противоположном орбитальному движению). Либрации возможных трехчастичных резонансов имеют амплитуды всего около 3 градусов, и моделирование показывает, что резонансная система устойчива к возмущениям. Тройных союзов не бывает.[40][30]
  • Кеплер-29 имеет пару планет в резонансе 7: 9 (соотношение 1 / 1,28587).[37]
  • Кеплер-36 имеет пару планет, близких к резонансу 6: 7.[41]
  • Кеплер-37 d, c и b находятся в пределах одного процента резонанса с соотношением орбит 8:15:24 и соотношением периодов 15: 8: 5 (39,792187, 21,301886 и 13,367308 дней).[42]
  • Из Кеплер-90 восьми известных планет, отношения периодов b: c, c: i и i: d близки к 4: 5, 3: 5 и 1: 4 соответственно (4: 4,977, 3: 4,97 и 1: 4,13) и d, e, f, g и h близки к соотношению периодов 2: 3: 4: 7: 11 (2: 3,078: 4,182: 7,051: 11,102; также 7: 11,021).[43][30] f, g и h также близки к соотношению периодов 3: 5: 8 (3: 5,058: 7,964).[44] Применимо к подобным системам и системам Кеплер-36, расчеты показывают, что присутствие внешней газовой планеты-гиганта способствует образованию плотноупакованных резонансов между внутренними суперземлями.[45]
  • HD 41248 есть пара суперземли в пределах 0,3% от резонанса 5: 7 (соотношение 1 / 1,39718).[46]
  • TRAPPIST-1 Семь планет размером примерно с Землю находятся в цепочке близких резонансов (самая длинная из известных цепей), имеющих отношение орбит примерно 24, 15, 9, 6, 4, 3 и 2, или отношения периодов ближайших соседей ( двигаясь наружу) примерно на 8/5, 5/3, 3/2, 3/2, 4/3 и 3/2 (1,603, 1,672, 1,506, 1,509, 1,342 и 1,519). Они также сконфигурированы так, что каждая тройка соседних планет находится в резонансе Лапласа (то есть b, c и d в одной такой конфигурации Лапласа; c, d и e в другой и т. Д.).[47][31] Ожидается, что резонансная конфигурация будет стабильной в течение миллиардов лет, если предположить, что она возникла во время планетарной миграции.[48][49] Дана музыкальная интерпретация резонанса.[49]
  • К2-138 имеет 5 подтвержденных планет в непрерывной резонансной цепочке, близкой к 3: 2 (с периодами 2,353, 3,560, 5,405, 8,261 и 12,758 дней). Система была обнаружена в гражданская наука проект Exoplanet Explorers, используя данные K2.[50] К2-138 мог разместить коорбитальные тела (в резонансе среднего движения 1: 1).[51] Резонансные цепные системы могут стабилизировать коорбитальные тела[52] и специальный анализ кривой блеска K2 и лучевой скорости от HARPS может раскрыть их.[51] Последующие наблюдения с Космический телескоп Спитцера предположим, что шестая планета продолжает резонансную цепочку 3: 2, оставляя в ней два промежутка (ее период составляет 41,97 дня). Эти пробелы могут быть заполнены более мелкими непереходящими планетами.[53][54] Будущие наблюдения с ЧЕОПС будет измерять вариации времени прохождения системы для дальнейшего анализа массы планет и потенциально может найти другие планетные тела в системе.[55]
  • К2-32 имеет четыре планеты в близком резонансе 1: 2: 5: 7 (с периодами 4,34, 8,99, 20,66 и 31,71 дня). Планета e имеет радиус, почти идентичный радиусу Земли. Остальные планеты имеют размер между Нептуном и Сатурном.[56]
  • V1298 Тельца имеет четыре подтвержденных планеты, из которых планеты c, d и b находятся рядом с резонансом 1: 2: 3 (с периодами 8,25, 12,40 и 24,14 дня). Планета e показывает только один транзит на кривой блеска K2 и имеет период более 36 дней. Планета e может находиться в резонансе низкого порядка (2: 3, 3: 5, 1: 2 или 1: 3) с планетой b. Система очень молода (23 ± 4 Myr ) и может быть предшественником компактной многопланетной системы. Резонанс 2: 3 предполагает, что некоторые близкие планеты могут образовываться в резонансах или эволюционировать в них за время менее 10 млн лет. Планеты в системе имеют размер между Нептуном и Сатурном. Только планета b имеет размер, подобный Юпитеру.[57]
  • HD 158259 содержит четыре планеты в цепочке близких к резонансу 3: 2 (с периодами 3,432, 5,198, 7,954 и 12,03 дня или соотношениями периодов 1,51, 1,53 и 1,51 соответственно) с возможной пятой планетой также вблизи резонанса 3: 2 ( с периодом 17,4 суток). Экзопланеты были найдены Спектрограф SOPHIE échelle, с использованием радиальная скорость метод.[58]
  • Кеплер-1649 содержит две планеты размером с Землю, близкие к резонансу 9: 4 (с периодами 19,53527 и 8,689099 дней, или отношением периодов 2,24825), включая одну ("c" ) в жилой зоне. Необнаруженная планета с периодом 13,0 дней создаст резонансную цепочку 3: 2.[59]
  • Кеплер-88 имеет пару внутренних планет, близких к резонансу 1: 2 (отношение периодов 2,0396), с отношением масс ~ 22,5, что дает очень большие вариации времени прохождения ~ 0,5 дня для самой внутренней планеты. На орбите около 1400 дней находится еще более массивная внешняя планета.[60]

Случаи внесолнечных планет, близких к резонансу среднего движения 1: 2, довольно распространены. Шестнадцать процентов систем, обнаруженных метод транзита сообщается, что есть пример этого (с отношениями периодов в диапазоне 1,83–2,18),[37] а также одна шестая планетных систем, характеризующихся Доплеровская спектроскопия (с более узким диапазоном отношения периодов).[61] Из-за неполного знания систем фактические пропорции, вероятно, будут выше.[37] В целом, около трети систем с характеристиками лучевой скорости, по-видимому, имеют пару планет, близких к соизмеримость.[37][61] Для пар планет гораздо чаще отношение орбитальных периодов на несколько процентов больше, чем отношение резонансов среднего движения, чем на несколько процентов меньше (особенно в случае резонансов первого порядка, в которых целые числа в соотношении отличаются на единицу). ).[37] Это предсказывалось в случаях, когда приливные взаимодействия со звездой значительны.[62]

Совпадающие "близкие" отношения среднего движения

Изображение астероида Паллада 18: 7 около резонанса с Юпитером во вращающейся системе отсчета (нажмите для анимации). Юпитер (розовая петля вверху слева) почти неподвижен. Смещение орбиты Паллада относительно Юпитера со временем неуклонно увеличивается; он никогда не меняет курс (т.е. нет либрации).
Изображение земной шар:Венера 8:13 около резонанса. Когда Земля неподвижна в центре невращающейся системы отсчета, последующие нижние союзы Венеры за восемь земных лет прослеживают пентаграмматический узор (отражающий разницу чисел в соотношении).
Схема орбит Плутон маленькие внешние четыре луны, которые следуют последовательности близких резонансов 3: 4: 5: 6 относительно периода его большого внутреннего спутника Харон. Спутники Стикс, Никс и Гидра также участвуют в истинном 3-х корпусный резонанс.

Ряд почтицелое число -отношения между орбитальными частотами планет или больших лун иногда указываются (см. список ниже). Однако они не имеют динамического значения, потому что нет соответствующей прецессии перигелий или другой либрации для достижения идеального резонанса (см. подробное обсуждение в раздел выше ). Такие близкие резонансы динамически несущественны, даже если рассогласование довольно мало, потому что (в отличие от истинного резонанса) после каждого цикла относительное положение тел смещается. При усреднении по астрономически коротким временным масштабам их относительное положение является случайным, как и тела, которые далеки от резонанса. Например, рассмотрим орбиты Земли и Венеры, которые достигают почти одинаковой конфигурации после 8 орбит вокруг Земли и 13 орбит Венеры. Фактическое соотношение составляет 0,61518624, что всего на 0,032% отличается от точных 8:13. Несоответствие через 8 лет составляет всего 1,5 ° орбитального движения Венеры. Тем не менее, этого достаточно, чтобы Венера и Земля оказывались в противоположной относительной ориентации по отношению к оригиналу каждые 120 таких циклов, что составляет 960 лет. Следовательно, в масштабе времени в тысячи лет и более (все еще крошечных по астрономическим стандартам) их относительное положение фактически случайно.

Присутствие близкого резонанса может отражать то, что идеальный резонанс существовал в прошлом, или что система эволюционирует в сторону такого резонанса в будущем.

Некоторые совпадения орбитальной частоты включают:

Некоторые совпадения орбитальной частоты
(Соотношение) и телаНесоответствие после одного цикла[а]Время рандомизации[b]Вероятность[c]
Планеты
(9:23) Венера –Меркурий4.0°200 у0.19
(8:13) земной шар –Венера[63][64][d]1.5°1000 у0.065
(243:395) земной шар –Венера[63][65]0.8°50,000 у0.68
(1:3) Марс –Венера20.6°20 лет0.11
(1:2) Марс –земной шар42.9°8 лет0.24
(1:12) Юпитер –земной шар[e]49.1°40 лет0.28
(2:5) Сатурн –Юпитер[f]12.8°800 лет0.13
(1:7) Уран –Юпитер31.1°500 лет0.18
(7:20) Уран –Сатурн5.7°20000 лет0.20
(5:28) Нептун –Сатурн1.9°80 000 лет0.052
(1:2) Нептун –Уран14.0°2000 г0.078
Система Марса
(1:4) Деймос –Фобос[грамм]14.9°0,04 года0.083
Основные астероиды
(1:1) Паллада –Церера[67][68]0.7°1000 лет0.0039[час]
(7:18) Юпитер –Паллада[69]0.10°100000 лет0.0040[я]
87 Сильвия система[j]
(17:45) Ромул –Ремус0.7°40 лет0.067
Система Юпитера
(1:6) Ио –Метис0.6°2 года0.0031
(3:5) Амальтея –Адрастеа3.9°0,2 года0.064
(3:7) Каллисто –Ганимед[70]0.7°30 лет0.012
Система Сатурна
(2:3) Энцелад –Мимас33.2°0,04 года0.33
(2:3) Диона –Тетис[k]36.2°0,07 года0.36
(3:5) Рея –Диона17.1°0,4 года0.26
(2:7) Титан –Рея21.0°0,7 года0.22
(1:5) Япет –Титан9.2°4 года0.051
Основной кентавры[l]
(3:4) Уран –Чарикло4.5°10 000 лет0.073
Система урана
(3:5) Розалинда –Корделия[72]0.22°4 года0.0037
(1:3) Умбриэль –Миранда[м]24.5°0,08 года0.14
(3:5) Умбриэль –Ариэль[n]24.2°0,3 года0.35
(1:2) Титания –Умбриэль36.3°0,1 года0.20
(2:3) Оберон –Титания33.4°0,4 года0.34
Система Нептуна
(1:20) Тритон –Наяда13.5°0,2 года0.075
(1:2) Протей –Лариса[75][76]8.4°0,07 года0.047
(5:6) Протей –Гиппокамп2.1°1 год0.057
Система Плутона
(1:3) Стикс –Харон[77]58.5°0,2 года0.33
(1:4) Nix –Харон[77][78]39.1°0,3 года0.22
(1:5) Kerberos –Харон[77]9.2°2 года0.05
(1:6) Гидра –Харон[77][78]6.6°3 года0.037
Система Хаумеа
(3:8) Hiʻiaka –Намака[o]42.5°2 года0.55
  1. ^ Несоответствие орбитальной долготы внутреннего тела по сравнению с его положением в начале цикла (с циклом, определенным как п орбиты внешнего тела - см. ниже). Предполагаются круговые орбиты (т.е. прецессия не учитывается).
  2. ^ Время, необходимое для того, чтобы рассогласование от начальных относительных продольных орбитальных положений тел увеличилось до 180 °, округленное до ближайшего первого значащая цифра.
  3. ^ В вероятность случайного совпадения орбит с равным или меньшим несовпадением хотя бы один раз в п попытки, где п - целое число орбит внешнего тела за цикл, и предполагается, что рассогласование варьируется от 0 ° до 180 ° случайным образом. Значение рассчитывается как 1- (1- несоответствие / 180 °).п. Это грубый расчет, который дает лишь приблизительное представление об относительных вероятностях.
  4. ^ Двое рядом соизмеримость перечисленные для Земли и Венеры отражены во времени транзиты Венеры, которые встречаются парами с разницей в 8 лет, в цикле, который повторяется каждые 243 года.[63][65]
  5. ^ Ближний резонанс 1:12 между Юпитером и Землей вызывает Астероиды Алинды, которые занимают (или близки) резонанс 3: 1 с Юпитером, чтобы быть близкими к резонансу 1: 4 с Землей.
  6. ^ Этот близкий резонанс получил название Великое неравенство. Впервые он был описан Лаплас в серии статей, опубликованных 1784–1789 гг.
  7. ^ Резонансы с ныне исчезнувшей внутренней луной, вероятно, были вовлечены в формирование Фобоса и Деймоса.[66]
  8. ^ На основе правильный орбитальный период, 1684,869 и 1681,601 дня для Паллады и Цереры соответственно.
  9. ^ На основе правильный орбитальный период Паллады, 1684,869 дня и 4332,59 дня Юпитера.
  10. ^ 87 Сильвия это первый астероид, у которого обнаружено более одной луны.
  11. ^ Возможно, этот резонанс был занят в прошлом.[71]
  12. ^ Немного определения кентавров оговаривают, что они нерезонансные тела.
  13. ^ Возможно, этот резонанс был занят в прошлом.[73]
  14. ^ Возможно, этот резонанс был занят в прошлом.[74]
  15. ^ Результаты для системы Хаумеа не очень значимы, потому что, вопреки предположениям, подразумеваемым в расчетах, Намака имеет эксцентричный, некеплеровский орбита, которая быстро прецессирует (см. ниже). Hiʻiaka и Namaka гораздо ближе к резонансу 3: 8, чем указано, и могут действительно находиться в нем.[79]

Наименее вероятная орбитальная корреляция в списке - это орбитальная корреляция между Ио и Метидой, за которой следуют орбитальные корреляции между Розалиндой и Корделией, Палладой и Церерой, Юпитером и Палладой, Каллисто и Ганимедом, Гидрой и Хароном соответственно.

Возможные прошлые резонансы среднего движения

Прошлый резонанс между Юпитером и Сатурном, возможно, сыграл драматическую роль в ранней истории Солнечной системы. 2004 г. компьютерная модель к Алессандро Морбиделли из Observatoire de la Côte d'Azur в Отлично предположил, что формирование резонанса 1: 2 между Юпитером и Сатурном (из-за взаимодействия с планетезимали это заставило их перемещаться внутрь и наружу соответственно) создавал гравитационный толчок, который продвигал Уран и Нептун на более высокие орбиты, а в некоторых сценариях заставлял их менять местами, что удвоило бы расстояние Нептуна от Солнца. Результирующее изгнание объектов из прото-Койперского пояса при движении Нептуна могло объяснить Поздняя тяжелая бомбардировка Через 600 миллионов лет после образования Солнечной системы и возникновения Юпитера. Троянские астероиды.[80] Миграция Нептуна наружу может также объяснить текущую занятость некоторых из его резонансов (особенно резонанса 2: 5) в пределах пояса Койпера.

В то время как спутники Сатурна среднего размера Диона и Тетис сейчас не близки к точному резонансу, они, возможно, были в резонансе 2: 3 в начале истории Солнечной системы. Это привело бы к эксцентриситету орбиты и приливное отопление это могло настолько согреть внутренность Тетиса, что образовался подземный океан. Последующее замерзание океана после того, как луны вырвались из резонанса, могло вызвать напряжения растяжения, которые создали огромные грабен система Итака Часма на Тетис.[71]

Спутниковая система Урана заметно отличается от систем Юпитера и Сатурна тем, что в ней отсутствуют точные резонансы между более крупными лунами, в то время как большинство более крупных спутников Юпитера (3 из 4 самых больших) и Сатурна (6 из 8 крупнейших) ) находятся в резонансах среднего движения. Во всех трех спутниковых системах спутники, вероятно, были захвачены в резонансы среднего движения в прошлом, поскольку их орбиты смещались из-за приливная диссипация (процесс, при котором спутники приобретают орбитальную энергию за счет энергии вращения первичной обмотки, непропорционально влияя на внутренние спутники). Однако в системе Урана из-за меньшей сжатие, и из-за большего относительного размера его спутников выйти из резонанса среднего движения намного легче. Более низкая сплющенность первичной обмотки изменяет ее гравитационное поле таким образом, что различные возможные резонансы располагаются более близко друг к другу. Чем больше относительный размер спутников, тем сильнее их взаимодействие. Оба фактора приводят к более хаотичному орбитальному поведению при резонансах среднего движения или вблизи них. Уход из резонанса может быть связан с захватом во вторичный резонанс и / или с увеличением мощности, вызванным приливной эволюцией. орбитальный эксцентриситет или же склонность.

Резонансы среднего движения, которые, вероятно, когда-то существовали в системе Урана, включают (3: 5) Ариэль-Миранду, (1: 3) Умбриэль-Миранду, (3: 5) Умбриэль-Ариэль и (1: 4) Титанию-Ариэль.[74][73] Доказательства таких прошлых резонансов включают относительно высокие эксцентриситет орбит внутренних спутников Урана и аномально высокое наклонение орбиты Миранды. Высокие эксцентриситета орбиты в прошлом, связанные с резонансами (1: 3) Умбриэль-Миранда и (1: 4) Титания-Ариэль, возможно, привели к приливному нагреву внутренних частей Миранды и Ариэля.[81] соответственно. Миранда, вероятно, вышла из своего резонанса с Умбриэлем через вторичный резонанс, и считается, что механизм этого побега объясняет, почему ее орбитальное наклонение более чем в 10 раз больше, чем у другого. обычный Уранские луны (см. Естественные спутники Урана ).[82][83]

Как и в случае с Мирандой, нынешние склонности лун Юпитера Амальтеи и Бытие считаются признаками прошлого прохождения через резонансы 3: 1 и 4: 2 с Ио соответственно.[84]

Полагают, что обычные спутники Нептуна Протей и Лариса прошли через резонанс 1: 2 несколько сотен миллионов лет назад; с тех пор луны отдалились друг от друга, потому что Протей находится вне синхронная орбита а Лариса в одном. Считается, что прохождение через резонанс возбудило эксцентриситет обеих лун до такой степени, которая с тех пор полностью не погашена.[75][76]

В случае Плутон '' спутников, было высказано предположение, что настоящие близкие резонансы являются пережитками предыдущего точного резонанса, который был нарушен приливным затуханием эксцентриситета орбиты Харона (см. Естественные спутники Плутона подробнее). Ближний резонанс может поддерживаться 15% -ной локальной флуктуацией гравитационного поля Плутон-Харон. Таким образом, эти близкие резонансы не могут быть случайными.

Меньшая внутренняя луна карликовая планета Хаумеа, Намака, составляет одну десятую массы большей внешней луны, Hiʻiaka. Намака вращается вокруг Хаумеа за 18 дней в эксцентричном, некеплеровский орбита, а по состоянию на 2008 г. наклонена на 13 ° от Хииаки.[79] В масштабе времени системы она должна была перейти на более круговую орбиту. Похоже, что он был нарушен резонансами с более массивным Хияка из-за сходящихся орбит, когда он двигался от Хаумеа из-за приливной диссипации. Спутники могли быть захвачены, а затем несколько раз выходили из орбитального резонанса. Вероятно, они прошли через резонанс 3: 1 относительно недавно и в настоящее время находятся в резонансе 8: 3 или, по крайней мере, близки к нему. Орбита Намаки сильно возмущенный, с текущей прецессией около −6,5 ° в год.[79]

Смотрите также

Примечания

  1. ^ Природу этого резонанса (игнорируя такие тонкости, как либрация и прецессия) можно грубо получить из орбитальных периодов следующим образом. От Showalter и другие., 2019,[29] периоды Наяды (Pn) и Талассы (Pt) равны 0,294396 и 0,311484 дня соответственно. Исходя из этого, период между соединениями может быть рассчитан как 5,366 дня (1 / [1 / Pn - 1 / Pt]), что составляет 18,23 (≈ 18,25) орбиты Наяды и 17,23 (≈ 17,25) орбиты Талассы. Таким образом, после четырех периодов соединения, 73 орбиты Наяды и 69 орбит Талассы истекли, и первоначальная конфигурация будет восстановлена.

Рекомендации

  1. ^ «Генеральная ассамблея IAU 2006: резолюции 5 и 6» (PDF). IAU. 24 августа 2006 г.. Получено 23 июн 2009.
  2. ^ а б Порко, К.; Николсон, П. Д.; Borderies, N .; Danielson, G.E .; Гольдрайх, П.; Холдберг, Дж. Б .; Лейн, А. Л. (1984). "Эксцентричные сатурнианские локоны при 1,29Rs и 1.45Rs". Икар. 60 (1): 1–16. Bibcode:1984Icar ... 60 .... 1P. Дои:10.1016/0019-1035(84)90134-9.
  3. ^ Rosen, P.A .; Лиссауэр, Дж. Дж. (1988). "Узловая изгибающая волна Титана −1: 0 в кольце С Сатурна". Наука. 241 (4866): 690–694. Bibcode:1988Научный ... 241..690R. Дои:10.1126 / science.241.4866.690. PMID  17839081. S2CID  32938282.
  4. ^ Chakrabarti, S.K .; Бхаттачарья, А. (2001). «Ограничения на параметры кольца С Сатурна при резонансе Титана -1: 0». Ежемесячные уведомления Королевского астрономического общества. 326 (2): L23. Bibcode:2001МНРАС.326Л..23С. Дои:10.1046 / j.1365-8711.2001.04813.x.
  5. ^ Витце, А. (5 сентября 2018 г.). «В поисках решения проблемы космического мусора на Земле». Природа. 561 (7721): 24–26. Bibcode:2018Натура.561 ... 24Вт. Дои:10.1038 / d41586-018-06170-1. PMID  30185967.
  6. ^ Daquin, J .; Rosengren, A.J .; Alessi, E.M .; Deleflie, F .; Valsecchi, G.B .; Росси, А. (2016). «Динамическая структура региона СОО: долговременная стабильность, хаос и перенос». Небесная механика и динамическая астрономия. 124 (4): 335–366. arXiv:1507.06170. Bibcode:2016CeMDA.124..335D. Дои:10.1007 / s10569-015-9665-9. S2CID  119183742.
  7. ^ Wiegert, P .; Коннорс, М .; Вейе, К. (30 марта 2017 г.). «Ретроградный соорбитальный астероид Юпитер». Природа. 543 (7647): 687–689. Bibcode:2017Натура.543..687Вт. Дои:10.1038 / природа22029. PMID  28358083. S2CID  205255113.
  8. ^ а б Мораис, М. Х. М .; Намуни, Ф. (21 сентября 2013 г.). «Астероиды в ретроградном резонансе с Юпитером и Сатурном». Ежемесячные уведомления о письмах Королевского астрономического общества. 436: L30 – L34. arXiv:1308.0216. Bibcode:2013МНРАС.436Л..30М. Дои:10.1093 / mnrasl / slt106. S2CID  119263066.
  9. ^ Барнс, Р. (2011). «Резонанс Лапласа». В Гарго, М. (ред.). Энциклопедия астробиологии. Springer Science + Business Media. С. 905–906. Дои:10.1007/978-3-642-11274-4_864. ISBN  978-3-642-11271-3.
  10. ^ а б c Rivera, E.J .; Laughlin, G .; Батлер, Р. П .; Vogt, S. S .; Haghighipour, N .; Мескиари, С. (2010). «Обзор экзопланет Лика-Карнеги: четвертая планета с массой Урана для GJ 876 во внесолнечной конфигурации Лапласа». Астрофизический журнал. 719 (1): 890–899. arXiv:1006.4244. Bibcode:2010ApJ ... 719..890R. Дои:10.1088 / 0004-637X / 719/1/890. S2CID  118707953.
  11. ^ Marti, J. G .; Giuppone, C.A .; Beauge, C. (2013). «Динамический анализ резонанса Лапласа Gliese-876». Ежемесячные уведомления Королевского астрономического общества. 433 (2): 928–934. arXiv:1305.6768. Bibcode:2013МНРАС.433..928М. Дои:10.1093 / mnras / stt765. S2CID  118643833.
  12. ^ а б c d Шоуолтер, М. Р.; Гамильтон, Д. П. (2015). «Резонансные взаимодействия и хаотическое вращение малых спутников Плутона». Природа. 522 (7554): 45–49. Bibcode:2015Натура.522 ... 45S. Дои:10.1038 / природа14469. PMID  26040889. S2CID  205243819.
  13. ^ Murray, C.D .; Дермотт, С. Ф. (1999). Динамика солнечной системы. Издательство Кембриджского университета. п. 17. ISBN  978-0-521-57597-3.
  14. ^ Битти, Дж. К. (23 июля 2003 г.). "Почему Сатурн навеселе?". Небо и телескоп. Архивировано из оригинал 3 сентября 2009 г.. Получено 25 февраля 2009.
  15. ^ Ward, W. R .; Гамильтон, Д. П. (2004). "Наклон Сатурна. I. Аналитическая модель". Астрономический журнал. 128 (5): 2501–2509. Bibcode:2004AJ .... 128.2501W. Дои:10.1086/424533.
  16. ^ Гамильтон, Д. П .; Уорд, У. Р. (2004). "Наклон Сатурна. II. Численная модель". Астрономический журнал. 128 (5): 2510–2517. Bibcode:2004AJ .... 128.2510H. Дои:10.1086/424534. S2CID  33083447.
  17. ^ Ласкар, Дж. (2008). «Хаотическая диффузия в Солнечной системе». Икар. 196 (1): 1–15. arXiv:0802.3371. Bibcode:2008Icar..196 .... 1л. Дои:10.1016 / j.icarus.2008.02.017. S2CID  11586168.
  18. ^ Laskar, J .; Гастино, М. (2009). «Существование траекторий столкновения Меркурия, Марса и Венеры с Землей». Природа. 459 (7248): 817–819. Bibcode:2009Натура.459..817L. Дои:10.1038 / природа08096. PMID  19516336. S2CID  4416436.
  19. ^ Musotto, S .; Варад, Ф .; Мур, В .; Шуберт, Г. (2002). «Численное моделирование орбит галилеевых спутников». Икар. 159 (2): 500–504. Bibcode:2002Icar..159..500M. Дои:10.1006 / icar.2002.6939.
  20. ^ Браун, М.Э.; Баркуме, К. М .; Ragozzine, D .; Шаллер, Э. Л. (2007). «Коллизионное семейство ледяных объектов в поясе Койпера» (PDF). Природа. 446 (7133): 294–296. Bibcode:2007Натура.446..294Б. Дои:10.1038 / природа05619. PMID  17361177. S2CID  4430027.
  21. ^ Ragozzine, D .; Браун, М. Э. (2007). «Кандидаты в члены и возрастная оценка семьи объекта пояса Койпера 2003 EL61». Астрономический журнал. 134 (6): 2160–2167. arXiv:0709.0328. Bibcode:2007AJ .... 134.2160R. Дои:10.1086/522334. S2CID  8387493.
  22. ^ Буйе, М. В. (24 октября 2011 г.). "Подгонка орбиты и астрометрический рекорд для 225088". SwRI (Отделение космических наук). Получено 14 ноября 2014.
  23. ^ Синклер, А. Т. (1975). "Орбитальный резонанс среди галилеевых спутников Юпитера". Ежемесячные уведомления Королевского астрономического общества. 171 (1): 59–72. Bibcode:1975МНРАС.171 ... 59С. Дои:10.1093 / mnras / 171.1.59.
  24. ^ Витце, А. (3 июня 2015 г.). «Спутники Плутона движутся синхронно». Новости природы. Дои:10.1038 / природа.2015.17681. S2CID  134519717.
  25. ^ Мальхотра, Р. (1997). "Орбита Плутона". Получено 26 марта 2007.
  26. ^ Браун, М.Э. (23 марта 2009 г.). «S / 2005 (90482) 1 нужна твоя помощь». Планеты Майка Брауна. Получено 25 марта 2009.
  27. ^ «НАСА обнаружило, что спутники Нептуна заблокированы в танце избегания»'". Лаборатория реактивного движения. 14 ноября 2019 г.. Получено 15 ноября 2019.
  28. ^ Брозович, М .; Шоуолтер, М. Р .; Jacobson, R.A .; French, R. S .; Lissauer, J. J .; де Патер, И. (31 октября 2019 г.). «Орбиты и резонансы регулярных спутников Нептуна». Икар. 338 (2): 113462. arXiv:1910.13612. Дои:10.1016 / j.icarus.2019.113462. S2CID  204960799.
  29. ^ Шоуолтер, М. Р .; де Патер, I .; Lissauer, J. J .; Французский, R. S.url = https://www.spacetelescope.org/static/archives/releases/science_papers/heic1904/heic1904a.pdf (2019). «Седьмая внутренняя луна Нептуна». Природа. 566 (7744): 350–353. Bibcode:2019Натура.566..350S. Дои:10.1038 / s41586-019-0909-9. ЧВК  6424524. PMID  30787452.
  30. ^ а б c Shale, C.J .; Вандербург, А. (2017). «Идентификация экзопланет с помощью глубокого обучения: резонансная цепочка пяти планет вокруг Кеплера-80 и восьмая планета вокруг Кеплера-90» (PDF). Астрофизический журнал. 155 (2): 94. arXiv:1712.05044. Bibcode:2018AJ .... 155 ... 94S. Дои:10.3847 / 1538-3881 / aa9e09. S2CID  4535051. Получено 15 декабря 2017.
  31. ^ а б Luger, R .; Сестович, М .; Kruse, E .; Grimm, S.L .; Демори, Б.-О .; Agol, E .; Bolmont, E .; Fabrycky, D .; Fernandes, C.S .; Van Grootel, V .; Бургассер, А .; Gillon, M .; Ingalls, J. G .; Jehin, E .; Raymond, S.N .; Selsis, F .; Triaud, A.H.M.J .; Barclay, T .; Barentsen, G .; Delrez, L .; de Wit, J .; Форман-Макки, Д .; Холдсворт, Д. Л .; Leconte, J .; Lederer, S .; Turbet, M .; Almleaky, Y .; Benkhaldoun, Z .; Magain, P .; Моррис, Б. (22 мая 2017 г.). «Семипланетная резонансная цепочка в TRAPPIST-1». Природа Астрономия. 1 (6): 0129. arXiv:1703.04166. Bibcode:2017НатАс ... 1E.129L. Дои:10.1038 / s41550-017-0129. S2CID  54770728.
  32. ^ Изидоро, А .; Огихара, М .; Raymond, S.N .; Morbidelli, A .; Pierens, A .; Bitsch, B .; Cossou, C .; Херсант, Ф. (2017). «Разрыв цепей: горячие системы суперземли от миграции и разрыва компактных резонансных цепочек». Ежемесячные уведомления Королевского астрономического общества. 470 (2): 1750–1770. arXiv:1703.03634. Bibcode:2017МНРАС.470.1750И. Дои:10.1093 / мнрас / stx1232. S2CID  119493483.
  33. ^ Лафлин, Г. (23 июня 2010 г.). «Второй резонанс Лапласа». Системный: характеристика планет. Архивировано из оригинал 29 декабря 2013 г.. Получено 30 июн 2015.
  34. ^ Марси, Ге. W .; Батлер, Р. П .; Fischer, D .; Vogt, S. S .; Lissauer, J. J .; Ривера, Э. Дж. (2001). "Пара резонансных планет, вращающихся вокруг GJ 876". Астрофизический журнал. 556 (1): 296–301. Bibcode:2001ApJ ... 556..296M. Дои:10.1086/321552.
  35. ^ "Планета Кеплер-223 б". Энциклопедия внесолнечных планет. Получено 21 января 2018.
  36. ^ Битти, К. (5 марта 2011 г.). «Кеплер находит планеты в напряженном танце». Небо и телескоп. Получено 16 октября 2012.
  37. ^ а б c d е ж Лиссауэр, Дж. Дж.; и другие. (2011). «Архитектура и динамика системы многократных транзитных планет-кандидатов Кеплера». Серия дополнений к астрофизическому журналу. 197 (1): 1–26. arXiv:1102.0543. Bibcode:2011ApJS..197 .... 8л. Дои:10.1088/0067-0049/197/1/8. S2CID  43095783.
  38. ^ а б Миллс, С. М .; Fabrycky, D.C .; Мигашевский, Ц .; Ford, E.B .; Petigura, E .; Исааксон, Х. (11 мая 2016 г.). «Резонансная цепочка из четырех транзитных планет под Нептуном». Природа. 533 (7604): 509–512. arXiv:1612.07376. Bibcode:2016Натура.533..509М. Дои:10.1038 / природа17445. PMID  27225123. S2CID  205248546.
  39. ^ Коппес, С. (17 мая 2016 г.). "Система Кеплер-223: ключи к миграции планет". Лаборатория реактивного движения. Получено 18 мая 2016.
  40. ^ MacDonald, M. G .; Ragozzine, D .; Fabrycky, D.C .; Ford, E.B .; Holman, M. J .; Isaacson, H.T .; Lissauer, J. J .; Lopez, E.D .; Мазех, Т. (1 января 2016 г.). «Динамический анализ системы пяти транзитных планет Kepler-80». Астрономический журнал. 152 (4): 105. arXiv:1607.07540. Bibcode:2016AJ .... 152..105M. Дои:10.3847/0004-6256/152/4/105. S2CID  119265122.
  41. ^ Картер, Дж. А .; Agol, E .; Чаплин, В. Дж .; и другие. (21 июня 2012 г.). «Кеплер-36: пара планет с соседними орбитами и разной плотностью». Наука. 337 (6094): 556–559. arXiv:1206.4718. Bibcode:2012Sci ... 337..556C. Дои:10.1126 / science.1223269. PMID  22722249. S2CID  40245894.
  42. ^ Barclay, T .; и другие. (2013). «Экзопланета размером с Меркурий». Природа. 494 (7438): 452–454. arXiv:1305.5587. Bibcode:2013Натура.494..452Б. Дои:10.1038 / природа11914. PMID  23426260. S2CID  205232792.
  43. ^ Lissauer, J. J .; Marcy, G.W .; Bryson, S.T .; Rowe, J. F .; Jontof-Hutter, D .; Agol, E .; Borucki, W. J .; Картер, Дж. А .; Ford, E.B .; Gilliland, R.L .; Kolbl, R .; Звезда, К. М .; Steffen, J. H .; Торрес, Г. (25 февраля 2014 г.). «Валидация кандидатов на множественные планеты Кеплера. II: уточненная статистическая база и описания систем особого интереса». Астрофизический журнал. 784 (1): 44. arXiv:1402.6352. Bibcode:2014ApJ ... 784 ... 44L. Дои:10.1088 / 0004-637X / 784/1/44. S2CID  119108651.
  44. ^ Cabrera, J .; Csizmadia, Sz .; Lehmann, H .; Dvorak, R .; Gandolfi, D .; Rauer, H .; Эриксон, А .; Dreyer, C .; Eigmüller, Ph .; Хацес, А. (31 декабря 2013 г.). «Планетная система для KIC 11442793: компактный аналог Солнечной системы». Астрофизический журнал. 781 (1): 18. arXiv:1310.6248. Bibcode:2014ApJ ... 781 ... 18C. Дои:10.1088 / 0004-637X / 781/1/18. S2CID  118875825.
  45. ^ Руки, Т. О .; Александр, Р. Д. (13 января 2016 г.). «Могут быть гиганты: невидимые планеты массой Юпитера как скульпторы плотно упакованных планетных систем». Ежемесячные уведомления Королевского астрономического общества. 456 (4): 4121–4127. arXiv:1512.02649. Bibcode:2016МНРАС.456.4121Х. Дои:10.1093 / мнрас / stv2897. S2CID  55175754.
  46. ^ Jenkins, J. S .; Туоми, М .; Brasser, R .; Иванюк, О .; Мургас, Ф. (2013). «Две суперземли, вращающиеся вокруг солнечного аналога HD 41248 на границе среднего резонанса движения 7: 5». Астрофизический журнал. 771 (1): 41. arXiv:1304.7374. Bibcode:2013ApJ ... 771 ... 41J. Дои:10.1088 / 0004-637X / 771/1/41. S2CID  14827197.
  47. ^ Gillon, M .; Triaud, A.H.M.J .; Демори, Б.-О .; Jehin, E .; Agol, E .; Deck, K. M .; Lederer, S.M .; de Wit, J .; Бурданов, А. (22 февраля 2017 г.). «Семь планет земной группы с умеренным климатом вокруг ближайшей ультрахолодной карликовой звезды TRAPPIST-1». Природа. 542 (7642): 456–460. arXiv:1703.01424. Bibcode:2017Натура.542..456Г. Дои:10.1038 / природа21360. ЧВК  5330437. PMID  28230125.
  48. ^ Tamayo, D .; Rein, H .; Петрович, Ц .; Мюррей, Н. (10 мая 2017 г.). «Конвергентная миграция делает TRAPPIST-1 долговечным». Астрофизический журнал. 840 (2): L19. arXiv:1704.02957. Bibcode:2017ApJ ... 840L..19T. Дои:10.3847 / 2041-8213 / aa70ea. S2CID  119336960.
  49. ^ а б Чанг, К. (10 мая 2017 г.). «Гармония, которая защищает 7 миров размером с Землю Трапписта-1 от столкновения». Нью-Йорк Таймс. Получено 26 июн 2017.
  50. ^ Кристиансен, Джесси Л .; Crossfield, Ian J. M .; Barentsen, G .; Lintott, C.J .; Barclay, T .; Simmons, B.D .; Petigura, E .; Schlieder, J. E .; Дрессинг, C.D .; Вандербург, А .; Аллен, К. (11 января 2018 г.). «Система K2-138: почти резонансная цепочка из пяти субнептуновых планет, обнаруженных гражданскими учеными». Астрономический журнал. 155 (2): 57. arXiv:1801.03874. Bibcode:2018AJ .... 155 ... 57C. Дои:10.3847 / 1538-3881 / aa9be0. S2CID  52971376.
  51. ^ а б Lopez, T. A .; Баррос, С.С.C .; Santerne, A .; Deleuil, M .; Адибекян, В .; Almenara, J.-M .; Армстронг, Д. Дж .; Brugger, B .; Barrado, D .; Bayliss, D .; Boisse, I .; Бономо, А. С .; Bouchy, F .; Браун, Д. Дж. А .; Carli, E .; Demangeon, O .; Dumusque, X .; Díaz, R. F .; Faria, J. P .; Figueira, P .; Foxell, E .; Giles, H .; Hébrard, G .; Hojjatpanah, S .; Кирк, Дж .; Lillo-Box, J .; Lovis, C .; Mousis, O .; да Нобрега, Х. Дж .; Nielsen, L.D .; Neal, J. J .; Osborn, H.P .; Pepe, F .; Pollacco, D .; Santos, N.C .; Sousa, S.G .; Udry, S .; Виган, А .; Уитли, П. Дж. (1 ноября 2019 г.). «Характеристика экзопланеты в самой длинной известной резонансной цепи: система K2-138, наблюдаемая HARPS». Астрономия и астрофизика. 631: A90. arXiv:1909.13527. Bibcode:2019A & A ... 631A..90L. Дои:10.1051/0004-6361/201936267. S2CID  203593804.
  52. ^ Лелеу, Адриан; Coleman, Gavin A. L .; Атаи, С. (1 ноября 2019 г.). «Устойчивость коорбитального резонанса при диссипации - приложение к его эволюции в протопланетных дисках». Астрономия и астрофизика. 631: A6. arXiv:1901.07640. Bibcode:2019A & A ... 631A ... 6L. Дои:10.1051/0004-6361/201834486.
  53. ^ «Схема системы К2-138». www.jpl.nasa.gov. Получено 20 ноября 2019.
  54. ^ Hardegree-Ullman, K .; Кристиансен, Дж. (Январь 2019 г.). «K2-138 g: Спитцер обнаруживает шестой суб-Нептун для системы гражданской науки». Тезисы докладов собрания Американского астрономического общества № 233. 233: 164.07. Bibcode:2019AAS ... 23316407H.
  55. ^ «Программы АО-1 - Программа приглашенных наблюдателей CHEOPS - Космос». www.cosmos.esa.int. Получено 20 ноября 2019.
  56. ^ Хеллер, Рене; Роденбек, Кай; Хиппке, Майкл (1 мая 2019 г.). "Обзор методом наименьших квадратов транзита - I. Открытие и проверка планеты размером с Землю в системе четырех планет K2-32 вблизи резонанса 1: 2: 5: 7". Астрономия и астрофизика. 625: A31. arXiv:1904.00651. Bibcode:2019A & A ... 625A..31H. Дои:10.1051/0004-6361/201935276. ISSN  0004-6361. S2CID  90259349.
  57. ^ Дэвид, Тревор Дж .; Петигура, Эрик А .; Люгер, Родриго; Форман-Макки, Дэниел; Ливингстон, Джон Х .; Mamajek, Eric E .; Хилленбранд, Линн А. (29 октября 2019 г.). «Четыре новорожденных планеты, проходящие транзитом через молодой аналог Солнца V1298 Tau». Астрофизический журнал. 885 (1): L12. arXiv:1910.04563. Bibcode:2019ApJ ... 885L..12D. Дои:10.3847 / 2041-8213 / ab4c99. ISSN  2041-8213. S2CID  204008446.
  58. ^ Hara, N.C .; Bouchy, F .; Сталпорт, М .; Boisse, I .; Rodrigues, J .; Delisle, J.-B .; Santerne, A .; Генри, G.W .; Арнольд, Л .; Astudillo-Defru, N .; Боргниет, С. (2020). «Поиски SOPHIE северных внесолнечных планет. XVII. Компактная планетная система в цепочке резонанса среднего движения, близкой к 3: 2». Астрономия и астрофизика. 636: L6. arXiv:1911.13296. Дои:10.1051/0004-6361/201937254. S2CID  208512859.
  59. ^ Вандербург, А .; Rowden, P .; Bryson, S .; Coughlin, J .; Batalha, N .; Collins, K.A .; Latham, D.W .; Маллалли, S.E .; Colón, K.D .; Henze, C .; Huang, C.X .; Куинн, С. (2020). «Планета размером с Землю для обитаемой зоны, спасенная от ложноположительного статуса». Астрофизический журнал. 893 (1): L27. arXiv:2004.06725. Дои:10.3847 / 2041-8213 / ab84e5. S2CID  215768850.
  60. ^ Weiss, L.M .; Fabrycky, D.C .; Agol, E .; Миллс, S.M .; Howard, A.W .; Isaacson, H .; Petigura, E.A .; Fulton, B .; Hirsch, L .; Синуков, Э. (2020). «Открытие долгопериодической эксцентричной планеты Kepler-88 d и определение характеристик системы с помощью радиальных скоростей и фотодинамический анализ» (PDF). Астрономический журнал. 159 (5): 242. Дои:10.3847 / 1538-3881 / ab88ca. S2CID  202539420.
  61. ^ а б Wright, J. T .; Fakhouri, O .; Marcy, G.W .; Han, E .; Feng, Y .; Johnson, J. A .; Howard, A. W .; Фишер, Д. А .; Валенти, Дж. А .; Андерсон, Дж .; Пискунов, Н. (2011). "База данных орбит экзопланеты". Публикации Тихоокеанского астрономического общества. 123 (902): 412–42. arXiv:1012.5676. Bibcode:2011PASP..123..412W. Дои:10.1086/659427. S2CID  51769219.
  62. ^ Terquem, C .; Папалоизу, Дж. С. Б. (2007). «Миграция и образование систем горячих суперземель и Нептунов». Астрофизический журнал. 654 (2): 1110–1120. arXiv:astro-ph / 0609779. Bibcode:2007ApJ ... 654.1110T. Дои:10.1086/509497. S2CID  14034512.
  63. ^ а б c Лэнгфорд, П. М. (12 марта 2012 г.). «Проходы Венеры». Астрономическое общество Нормандского острова Гернси. Архивировано из оригинал 11 января 2012 г.. Получено 15 января 2016.
  64. ^ Bazsó, A .; Эйбл, В .; Dvorak, R .; Pilat-Lohinger, E .; Lhotka, C. (2010). «Обзор резонансов почти среднего движения между Венерой и Землей». Небесная механика и динамическая астрономия. 107 (1): 63–76. arXiv:0911.2357. Bibcode:2010CeMDA.107 ... 63B. Дои:10.1007 / s10569-010-9266-6. S2CID  117795811.
  65. ^ а б Шортт, Д. (22 мая 2012 г.). "Некоторые подробности про транзиты Венеры". Планетарное общество. Получено 22 мая 2012.
  66. ^ Rosenblatt, P .; Чарноз, С .; Dunseath, K. M .; Terao-Dunseath, M .; Trinh, A .; Hyodo, R .; Genda, H .; Тупин, С. (4 июля 2016 г.). «Аккреция Фобоса и Деймоса в протяженном диске обломков, перемешанном с переходными лунами» (PDF). Природа Геонауки. 9 (8): 581–583. Bibcode:2016NatGe ... 9..581R. Дои:10.1038 / ngeo2742.
  67. ^ Гоффин, Э. (2001). «Новое определение массы Паллады». Астрономия и астрофизика. 365 (3): 627–630. Bibcode:2001A & A ... 365..627G. Дои:10.1051/0004-6361:20000023.
  68. ^ Ковачевич, А. Б. (2012). «Определение массы Цереры на основе наиболее эффективных с точки зрения гравитации близких столкновений». Ежемесячные уведомления Королевского астрономического общества. 419 (3): 2725–2736. arXiv:1109.6455. Bibcode:2012МНРАС.419.2725К. Дои:10.1111 / j.1365-2966.2011.19919.x.
  69. ^ Тейлор, Д. Б. (1982). «Светское движение Паллады». Ежемесячные уведомления Королевского астрономического общества. 199 (2): 255–265. Bibcode:1982МНРАС.199..255Т. Дои:10.1093 / mnras / 199.2.255.
  70. ^ Гольдрайх, П. (1965). «Объяснение частого появления соизмеримых средних движений в солнечной системе». Ежемесячные уведомления Королевского астрономического общества. 130 (3): 159–181. Bibcode:1965МНРАС.130..159Г. Дои:10.1093 / mnras / 130.3.159.
  71. ^ а б Chen, E.MA .; Ниммо, Ф. (2008). «Тепловая и орбитальная эволюция Тетиса, ограниченная наблюдениями с поверхности» (PDF). Наука о Луне и планетах XXXIX. Лунно-планетарный институт. #1968. Получено 14 марта 2008.
  72. ^ Murray, C.D .; Томпсон, Р. П. (1990). «Орбиты спутников-пастухов, выведенные из структуры колец Урана». Природа. 348 (6301): 499–502. Bibcode:1990Натура.348..499М. Дои:10.1038 / 348499a0. S2CID  4320268.
  73. ^ а б Tittemore, W. C .; Мудрость, Дж. (1990). «Приливная эволюция спутников Урана: III. Эволюция через соизмеримость среднего движения Миранда-Умбриэль 3: 1, Миранда-Ариэль 5: 3 и Ариэль-Умбриэль 2: 1». Икар. 85 (2): 394–443. Bibcode:1990Icar ... 85..394T. Дои:10.1016 / 0019-1035 (90) 90125-С. HDL:1721.1/57632.
  74. ^ а б Tittemore, W. C .; Уиздом Дж. (1988). «Приливная эволюция спутников Урана I. Прохождение Ариэля и Умбриэля через соизмеримость среднего движения 5: 3». Икар. 74 (2): 172–230. Bibcode:1988Icar ... 74..172T. Дои:10.1016/0019-1035(88)90038-3. HDL:1721.1/57632.
  75. ^ а б Zhang, K .; Гамильтон, Д. П. (2007). "Орбитальные резонансы во внутренней системе Нептуна: I. Резонанс среднего движения Протея – Ларисы 2: 1". Икар. 188 (2): 386–399. Bibcode:2007Icar..188..386Z. Дои:10.1016 / j.icarus.2006.12.002.
  76. ^ а б Zhang, K .; Гамильтон, Д. П. (2008). «Орбитальные резонансы во внутренней системе Нептуна: II. Резонансная история Протея, Ларисы, Галатеи и Деспины». Икар. 193 (1): 267–282. Bibcode:2008Icar..193..267Z. Дои:10.1016 / j.icarus.2007.08.024.
  77. ^ а б c d Матсон, Дж. (11 июля 2012 г.). "Новолуние Плутона: телескоп Хаббла обнаружил пятый плутонический спутник". Scientific American. Получено 12 июля 2012.
  78. ^ а б Ward, W. R .; Кануп, Р. М. (2006). "Принудительная резонансная миграция внешних спутников Плутона Хароном". Наука. 313 (5790): 1107–1109. Bibcode:2006Научный ... 313.1107W. Дои:10.1126 / science.1127293. PMID  16825533. S2CID  36703085.
  79. ^ а б c Ragozzine, D .; Браун, М. Э. (2009). «Орбиты и массы спутников карликовой планеты Хаумеа = 2003 EL61». Астрономический журнал. 137 (6): 4766–4776. arXiv:0903.4213. Bibcode:2009AJ .... 137.4766R. Дои:10.1088/0004-6256/137/6/4766. S2CID  15310444.
  80. ^ Хансен, К. (7 июня 2004 г.). "Орбитальная перестановка для ранней солнечной системы". Geotimes. Получено 26 августа 2007.
  81. ^ Титтемор, В. К. (1990). «Приливное тепло Ариэля». Икар. 87 (1): 110–139. Bibcode:1990Icar ... 87..110T. Дои:10.1016/0019-1035(90)90024-4.
  82. ^ Tittemore, W. C .; Уиздом Дж. (1989). "Приливная эволюция спутников Урана II. Объяснение аномально высокого орбитального наклонения Миранды" (PDF). Икар. 78 (1): 63–89. Bibcode:1989Icar ... 78 ... 63T. Дои:10.1016/0019-1035(89)90070-5. HDL:1721.1/57632.
  83. ^ Malhotra, R .; Дермотт, С. Ф. (1990). «Роль вторичных резонансов в орбитальной истории Миранды». Икар. 85 (2): 444–480. Bibcode:1990Icar ... 85..444M. Дои:10.1016 / 0019-1035 (90) 90126-Т.
  84. ^ Burns, J. A .; Simonelli, D. P .; Шоуолтер, М. Р .; Гамильтон, Д. П .; Porco, C.C .; Эспозито, Л. У .; Труп, Х. (2004). "Система Кольцо-Луна Юпитера" (PDF). In Bagenal, F .; Dowling, T. E .; Маккиннон, В. Б. (ред.). Юпитер: планета, спутники и магнитосфера. Издательство Кембриджского университета. ISBN  978-0-521-03545-3.

внешняя ссылка