Апсидальная прецессия - Apsidal precession

Эта статья о вращении орбиты небесного тела. О прецессии оси вращения или изменении наклона орбиты см. Осевая прецессия.
Каждый планета на орбите солнце следует за эллиптическая орбита который постепенно вращается с течением времени (апсидальная прецессия). Этот рисунок иллюстрирует положительную апсидальную прецессию (продвижение перигелия), когда орбитальная ось поворачивается в том же направлении, что и орбитальное движение планеты. В эксцентриситет этого эллипса и скорость прецессии орбиты преувеличены для визуализации. Большинство орбит в Солнечная система имеют гораздо меньший эксцентриситет и прецессию с гораздо меньшей скоростью, что делает их почти круговой и стационарный.
Главный орбитальные элементы (или параметры). Линия апсид показана синим цветом и обозначена ω. Апсидальная прецессия - это скорость изменения ω через время, dω/dт.
Анимация Луныс орбита вокруг Земли - Полярный вид
  Луна ·   земной шар

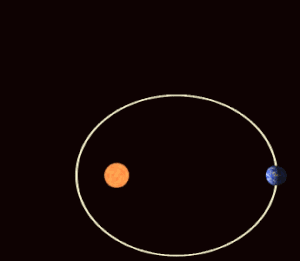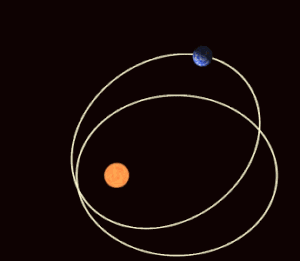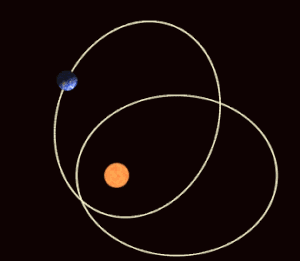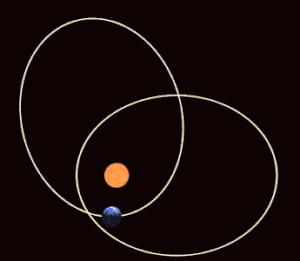
В небесная механика, апсидальная прецессия (или апсидное продвижение)[1] это прецессия (постепенное вращение) линии, соединяющей апсиды (линия апсид) астрономическое тело с орбита. Апсиды - это наиболее близкие (перицентрические) и наиболее удаленные (апоапсис) от него точки орбиты. основное тело. Апсидальная прецессия - первая производная по времени из аргумент перицентра, один из шести основных орбитальные элементы орбиты. Апсидальная прецессия считается положительной, если ось орбиты вращается в том же направлении, что и орбитальное движение. An апсидный период - временной интервал, необходимый для прецессии орбиты на 360 °.[2]

История

Древнегреческий астроном Hipparchos отметил апсидальную прецессию орбиты Луны;[3] это исправлено в Антикитерский механизм (около 80 г. до н.э.) с почти точным значением 8,88 лет на полный цикл, правильным в пределах 0,34%.[4] Прецессия солнечных апсид была открыта в XI веке. аз-Заркали.[5] В лунная апсидальная прецессия не было учтено в Клавдий Птолемей с Альмагест, и в совокупности эти прецессии, результат множества явлений, оставались трудными для объяснения до 20-го века, когда последняя неопознанная часть прецессии Меркурия была точно объяснена в Альберт Эйнштейн с общая теория относительности.[нужна цитата ]

Расчет

К прецессии периастра может привести множество факторов, таких как общая теория относительности, звездная квадруполь моменты, взаимные приливные деформации звезда – планета и возмущения от других планет.[6]

ωобщий = ωОбщая теория относительности + ωквадруполь + ωприлив + ωвозмущения

Для Меркурия скорость прецессии перигелия из-за общих релятивистских эффектов составляет 43 ″ (угловые секунды ) в столетие. Для сравнения, прецессия из-за возмущений от других планет Солнечной системы составляет 532 ″ за столетие, тогда как сжатие Солнца (квадрупольный момент) вызывает незначительный вклад 0,025 ″ за столетие.[7][8]

Согласно классической механике, если звезды и планеты рассматривать как чисто сферические массы, то они будут подчиняться простому 1/р2 закон обратных квадратов, связывая силу с расстоянием и, следовательно, выполняя замкнутые эллиптические орбиты в соответствии с Теорема Бертрана. Эффекты несферической массы вызваны приложением внешнего потенциала (ов): центробежный потенциал вращающихся тел, таких как вращение теста для пиццы, вызывает сплющивание полюсов, а сила тяжести соседней массы вызывает приливные выпуклости. Вращательные и чистые приливные выпуклости создают гравитационные квадрупольные поля (1/р3), которые приводят к прецессии орбиты.

Полная прецессия апсид для изолированных очень горячие юпитеры есть, учитывая только эффекты низшего порядка, и в целом в порядке важности

ωобщий = ωприливные возмущения + ωОбщая теория относительности + ωвращательные возмущения + ωвращательный * + ωприливный *

при этом планетарная приливная выпуклость является преобладающим термином, превышающим эффекты общей теории относительности и звездного квадруполя более чем на порядок. Хорошее результирующее приближение приливной выпуклости полезно для понимания недр таких планет. Для планет с самым коротким периодом внутренняя часть планеты вызывает прецессию на несколько градусов в год. До 19,9 ° в год для WASP-12b.[9][10]

Теорема Ньютона о вращающихся орбитах

Основная статья: Теорема Ньютона о вращающихся орбитах

Ньютон получил раннюю теорему, в которой пыталась объяснить прецессию апсид. Эта теорема исторически примечателен, но он никогда широко не использовался и предполагал силы, которых не было, что делало теорему недействительной. Эта теорема о вращающихся орбитах оставалась в значительной степени неизвестной и неразработанной более трех столетий до 1995 года.[11] Ньютон предположил, что изменения углового движения частицы можно объяснить добавлением силы, которая изменяется как обратный куб расстояния, не влияя на радиальное движение частицы.[нужна цитата ] Используя предшественника Серия Тейлор Ньютон обобщил свою теорему на все законы силы при условии, что отклонения от круговых орбит малы, что справедливо для большинства планет Солнечной системы.[нужна цитата ]. Однако его теорема не учитывала апсидальную прецессию Луны без отказа от закона обратных квадратов. Закон всемирного тяготения Ньютона. Кроме того, скорость апсидальной прецессии, рассчитанная с помощью теоремы Ньютона о вращающихся орбитах, не так точна, как для более новых методов, таких как теория возмущений.[нужна цитата ]

изменение орбиты с течением времени
Влияние апсидальной прецессии на времена года, когда эксцентриситет и ап / перигелий на орбите преувеличены для удобства просмотра. Показанные сезоны относятся к северному полушарию, а в южном полушарии времена года будут обратными в любой момент времени на орбите. Некоторые климатические эффекты возникают в основном из-за преобладания большего количества океанов в Южном полушарии.

Общая теория относительности

Основная статья: Проблема Кеплера в общей теории относительности

Апсидальная прецессия планеты Меркурий был отмечен Урбен Леверье в середине 19 века и объясняется Эйнштейна общая теория относительности.

Эйнштейн показал, что для планеты большая полуось его орбиты а, то эксцентриситет орбиты е и период революции Т, то апсидальная прецессия из-за релятивистских эффектов в течение одного периода обращения в радианы, является

куда c это скорость света.[12] В случае Меркурия половина большой оси находится примерно в 5.79×1010 м, эксцентриситет его орбиты равен 0,206, а период обращения 87,97 суток или 7.6×106 s. Отсюда и скорость света (~3×108 РС), можно рассчитать, что прецессия апсид за один период обращения равна ε = 5.028×10−7 радианы (2.88×10−5 градусов или 0,104 ″). За сто лет Меркурий делает примерно 415 оборотов вокруг Солнца, и, таким образом, за это время апсидальный перигелий из-за релятивистских эффектов составляет примерно 43 дюйма, что почти точно соответствует ранее необъясненной части измеренного значения.

Долгосрочный климат

Апсидальная прецессия Земли медленно увеличивает ее аргумент перицентра; она занимает около 112,000 лет, чтобы эллипс один раз повернулся относительно неподвижных звезд.[13] Полярная ось Земли и, следовательно, солнцестояния и равноденствия прецессируют с периодом около 26,000 лет по отношению к неподвижным звездам. Эти две формы «прецессии» сочетаются так, что происходит между 20,800 и 29,000 лет (и в среднем 23,000 лет), чтобы эллипс совершил один оборот относительно точки весеннего равноденствия, то есть, чтобы перигелий вернулся к той же дате (с учетом календаря, который точно отслеживает времена года).[14]

Это взаимодействие между аномалистическим и тропическим циклами важно для долгосрочные колебания климата на Земле, называется Циклы Миланковича. Также известен эквивалент на Марсе.

На рисунке справа показано влияние прецессии на сезоны северного полушария относительно перигелия и афелия. Обратите внимание, что площади, подметаемые в течение определенного сезона, меняются со временем. Орбитальная механика требует, чтобы продолжительность сезонов была пропорциональна охватываемым областям сезонных квадрантов, поэтому, когда орбитальный эксцентриситет является экстремальным, сезоны на обратной стороне орбиты могут быть значительно более продолжительными.

Смотрите также

Примечания

  1. ^ Боулер, М. Г. (2010). «Апсидальное продвижение в SS 433?». Астрономия и астрофизика. 510 (1): A28. arXiv:0910.3536. Bibcode:2010A и A ... 510A..28B. Дои:10.1051/0004-6361/200913471.
  2. ^ Хилдич, Р. В. (2001). Введение в близкие двойные звезды. Кембриджская серия по астрофизике. Издательство Кембриджского университета. п. 132. ISBN  9780521798006.
  3. ^ Джонс, А., Александр (сентябрь 1991 г.). «Адаптация вавилонских методов в греческой численной астрономии» (PDF). Исида. 82 (3): 440–453. Bibcode:1991Isis ... 82..441J. Дои:10.1086/355836.
  4. ^ Фрит, Тони; Бицакис, Янис; Муссас, Ксенофонт; Сейрадакис, Джон. ЧАС.; Целикас, А .; Mangou, H .; Zafeiropoulou, M .; Hadland, R .; и другие. (30 ноября 2006 г.). «Расшифровка древнегреческого астрономического калькулятора, известного как антикиферский механизм» (PDF). Природа. 444 Приложение (7119): 587–91. Bibcode:2006Натура.444..587F. Дои:10.1038 / природа05357. PMID  17136087. Архивировано из оригинал (PDF) 20 июля 2015 г.. Получено 20 мая 2014.
  5. ^ Тумер, Дж. Дж. (1969), "Солнечная теория аз-Заркала: история ошибок", Центавр, 14 (1): 306–336, Bibcode:1969Cent ... 14..306T, Дои:10.1111 / j.1600-0498.1969.tb00146.x, at pp. 314–317.
  6. ^ Дэвид М. Киппинг (8 августа 2011 г.). Транзиты внесолнечных планет с лунами. Springer. С. 84–. ISBN  978-3-642-22269-6. Получено 27 августа 2013.
  7. ^ Kane, S. R .; Хорнер, Дж .; фон Браун, К. (2012). "Вероятности циклического перехода долгопериодических эксцентрических планет из-за прецессии периастра". Астрофизический журнал. 757 (1): 105. arXiv:1208.4115. Bibcode:2012ApJ ... 757..105K. Дои:10.1088 / 0004-637x / 757/1/105.
  8. ^ Ричард Фицпатрик (30 июня 2012 г.). Введение в небесную механику. Издательство Кембриджского университета. п. 69. ISBN  978-1-107-02381-9. Получено 26 августа 2013.
  9. ^ Ragozzine, D .; Вольф, А. С. (2009). «Исследование внутренних пространств очень горячих юпитеров с помощью кривых транзитного блеска». Астрофизический журнал. 698 (2): 1778. arXiv:0807.2856. Bibcode:2009ApJ ... 698.1778R. Дои:10.1088 / 0004-637x / 698/2/1778.
  10. ^ Майкл Перриман (26 мая 2011 г.). Справочник экзопланеты. Издательство Кембриджского университета. С. 133–. ISBN  978-1-139-49851-7. Получено 26 августа 2013.
  11. ^ Чандрасекхар, стр. 183.
  12. ^ Хокинг, Стивен. На плечах гигантов: великие труды по физике и астрономии. Филадельфия, Пенсильвания, США: Бегущий пресс. pp. der Physik. ISBN  0-7624-1348-4.
  13. ^ ван ден Хеувель, Э. П. Дж. (1966). «О прецессии как причине плейстоценовых колебаний температуры воды Атлантического океана». Международный геофизический журнал. 11: 323–336. Bibcode:1966GeoJ ... 11..323V. Дои:10.1111 / j.1365-246X.1966.tb03086.x.
  14. ^ Времена года и орбита Земли, Военно-морская обсерватория США, получено 16 августа 2013