Приливная блокировка - Tidal locking
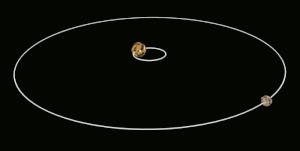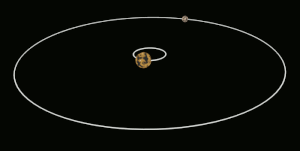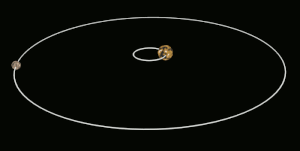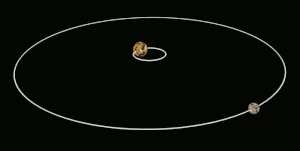
Приливная блокировка (также называется гравитационная блокировка, захваченное вращение и спин-орбитальная синхронизация) в наиболее известном случае происходит, когда на орбите астрономическое тело всегда обращен лицом к объекту, вокруг которого он вращается. Это известно как синхронное вращение: приливно заблокированному телу требуется столько же времени, чтобы вращаться вокруг своей оси, так и вращаться вокруг своего партнера. Например, та же сторона Луна всегда сталкивается с Земля, хотя есть некоторые изменчивость потому что орбита Луны не идеально круглая. Обычно только спутниковое приливно привязан к большему телу.[1] Однако, если разница в массе между двумя телами и расстояние между ними относительно невелики, каждое из них может быть приливно привязано друг к другу; это случай для Плутон и Харон.
Эффект возникает между двумя телами, когда их гравитационное взаимодействие замедляет вращение тела до тех пор, пока оно не становится приливным. За многие миллионы лет силы взаимодействия изменяют их орбиты и скорость вращения в результате обмена энергией и тепла. рассеяние. Когда одно из тел достигает состояния, при котором больше не происходит каких-либо чистых изменений в скорости его вращения в течение полного обращения по орбите, это называется приливной блокировкой.[2] Объект имеет тенденцию оставаться в этом состоянии, когда для выхода из него потребуется добавить энергию обратно в систему. Орбита объекта может со временем перемещаться, чтобы отменить приливную блокировку, например, если гигантская планета возмущает объект.
Не каждый случай приливной блокировки предполагает синхронное вращение.[3] С участием Меркурий, например, эта планета с приливной синхронизацией совершает три оборота за каждые два оборота вокруг Солнца, спин-орбитальный резонанс 3: 2. В особом случае, когда орбита почти круглая, а ось вращения тела не наклонена значительно, например, Луна, приливная блокировка приводит к тому, что одно и то же полушарие вращающегося объекта постоянно обращено к своему партнеру.[2][3][4]Однако в этом случае одна и та же часть тела не всегда обращена к партнеру на всех орбитах. Может быть некоторое смещение из-за вариации в орбитальной скорости запертого тела и наклоне оси его вращения.
Механизм

Рассмотрим пару объектов A и B, вращающихся на одной орбите. скорость вращения необходимость приливной фиксации тела B к большему телу A вызвана крутящий момент применяется сила тяжести на балджах, которые он создал на B приливные силы.[5]
Гравитационная сила от объекта A на B будет меняться с расстоянием, будучи наибольшей на ближайшей к A поверхности и наименьшей на самой удаленной. Это создает гравитационный градиент через объект B, что исказит его равновесие форма слегка. Тело объекта B станет вытянутым вдоль оси, ориентированной на A, и, наоборот, немного уменьшится в размерах по направлениям ортогональный к этой оси. Удлиненные искажения известны как приливные выпуклости. (Для твердой Земли эти выпуклости могут достигать смещения примерно до 0,4 метра (1,3 фута).[6]) Когда B еще не заблокирован приливом, выпуклости перемещаются по его поверхности из-за орбитальных движений, причем одна из двух "высоких" приливных выпуклостей движется близко к точке, где тело A находится над головой. Для больших астрономических тел, которые почти сферический из-за самогравитации приливное искажение вызывает слегка вытянутый сфероид, т.е. аксиально-симметричный эллипсоид которая вытянута вдоль большой оси. Меньшие тела также испытывают искажения, но это искажение менее регулярное.
Материал B оказывает сопротивление этому периодическому изменению формы, вызванному приливной силой. Фактически, требуется некоторое время, чтобы преобразовать B в форму гравитационного равновесия, к этому времени формирующиеся выпуклости уже отнесены на некоторое расстояние от оси A – B за счет вращения B. Если смотреть с выгодной точки в пространстве, точки максимального расширения выпуклости смещены от оси, ориентированной к A. Если период вращения B короче, чем его орбитальный период, выпуклости переносятся вперед от оси, ориентированной к A, в направлении вращения. , тогда как если период вращения B больше, выпуклости вместо этого отстают.
Поскольку выпуклости теперь смещены от оси A – B, гравитационное притяжение A к массе в них оказывает крутящий момент на B. Крутящий момент на выпуклости, обращенной к A, приводит вращение B в соответствие с его орбитальным периодом, тогда как " задняя "выпуклость", обращенная от A, действует в противоположном смысле. Однако выпуклость на стороне, обращенной к A, ближе к A, чем выпуклость на спине, на расстояние примерно диаметра B, и поэтому испытывает немного более сильную гравитационную силу и крутящий момент. Таким образом, результирующий крутящий момент от обоих выпуклостей всегда находится в том направлении, которое синхронизирует вращение B с его орбитальным периодом, что в конечном итоге приводит к приливной блокировке.
Орбитальные изменения
В угловой момент всей системы A – B сохраняется в этом процессе, так что, когда B замедляется и теряет угловой момент вращения, его орбитальный угловой момент увеличивается на аналогичную величину (есть также некоторые меньшие эффекты на вращение A). Это приводит к увеличению орбиты B вокруг A в тандеме с его замедлением вращения. В другом случае, когда B начинает вращаться слишком медленно, приливная блокировка и ускоряет его вращение, и понижает его орбита.
Блокировка большего тела
Эффект приливной блокировки также ощущается большим телом A, но с меньшей скоростью, потому что гравитационный эффект B слабее из-за меньшей массы B. Например, вращение Земли постепенно замедляется Луной на величину, которая становится заметной с течением геологического времени, как показано в летописи окаменелостей.[7] По текущим оценкам, это (вместе с приливным влиянием Солнца) помогло удлинить земные сутки примерно с 6 часов до нынешних 24 часов (более ≈ 4½ миллиарда лет). В настоящее время, атомные часы показывают, что земной день удлиняется в среднем примерно на 2,3 миллисекунды за столетие.[8] При наличии достаточного времени это создаст взаимную приливную блокировку между Землей и Луной. Длина Земли день увеличится и длина лунный месяц также увеличится. Звездные сутки Земли в конечном итоге будут иметь ту же длину, что и звездные сутки. Орбитальный период Луны, что примерно в 47 раз длиннее земных суток в настоящее время. Однако не ожидается, что Земля будет приливно привязана к Луне до того, как Солнце станет красный гигант и поглощает Землю и Луну.[9][10]
Для тел одинакового размера эффект может быть сопоставимого размера для обоих, и оба могут стать приливно привязанными друг к другу в гораздо более короткие сроки. Примером может служить карликовая планета Плутон и его спутник Харон. Они уже достигли состояния, когда Харон виден только из одного полушария Плутона и наоборот.[11]
Эксцентрические орбиты
Широко распространено заблуждение, что тело, запертое приливом, постоянно поворачивается одной стороной к своему хозяину.
— Heller et al. (2011)[3]
Для орбит, у которых эксцентриситет не близок к нулю, вращение ставка имеет тенденцию быть заблокированной с орбитальная скорость когда тело в перицентр, которая является точкой самого сильного приливного взаимодействия между двумя объектами. Если у вращающегося вокруг объекта есть спутник, это третье тело может вызвать колебательное изменение скорости вращения родительского объекта. Это взаимодействие также может приводить к увеличению эксцентриситета орбиты вращающегося вокруг первичного объекта - эффект, известный как накачка эксцентриситета.[12]
В некоторых случаях, когда орбита эксцентричный и приливный эффект относительно слаб, меньшее тело может оказаться в так называемом спин-орбитальный резонанс, вместо того, чтобы быть запертым. Здесь отношение периода вращения тела к его собственному периоду обращения представляет собой некоторую простую дробь, отличную от 1: 1. Хорошо известный случай - вращение Меркурий, который привязан к своей орбите вокруг Солнца в резонансе 3: 2.
Ожидается, что многие экзопланеты (особенно близкие) будут находиться в спин-орбитальных резонансах выше 1: 1. Планета земной группы, подобная Меркурию, может, например, быть захвачена в спин-орбитальный резонанс 3: 2, 2: 1 или 5: 2, причем вероятность каждого из них зависит от эксцентриситета орбиты.[13]
Вхождение
Луны

Самые крупные луны в Солнечная система, то гравитационно закругленные спутники, приливно привязаны к своим основным элементам, потому что они вращаются очень близко, и приливная сила быстро увеличивается (как кубическая функция ) с уменьшением расстояния.[14] Заметными исключениями являются неправильные внешние спутники газовые гиганты, которые вращаются намного дальше, чем большие известные спутники.
Плутон и Харон являются крайним примером приливной блокировки. Харон - относительно большая луна по сравнению с ее первичным спутником, а также имеет очень близкую орбита. Это приводит к взаимной блокировке Плутона и Харона. Другие спутники Плутона не заблокированы приливом; Стикс, Nix, Kerberos, и Гидра все вращаются хаотично из-за влияния Харона.
Ситуация приливной блокировки для астероидные луны в значительной степени неизвестно, но близкие по орбите двоичные файлы, как ожидается, будут заблокированы приливом, а также контактные двоичные файлы.
Луна Земли

Вращение Луны и орбитальные периоды приливно связаны друг с другом, поэтому независимо от того, когда Луна наблюдается с Земли, всегда видно одно и то же полушарие Луны. В обратная сторона луны не был замечен до 1959 года, когда фотографии большей части дальней стороны были переданы с Советский космический корабль Луна 3.[15]
Когда за Землей наблюдают с Луны, кажется, что Земля не движется по небу, а остается на том же месте, вращаясь вокруг своей оси.[16]
Несмотря на то, что периоды вращения и орбиты Луны точно синхронизированы, около 59 процентов всей поверхности Луны можно увидеть при повторных наблюдениях с Земли из-за явлений либрация и параллакс. Либрации в первую очередь вызваны изменяющейся орбитальной скоростью Луны из-за эксцентриситет его орбиты: это позволяет видеть с Земли примерно на 6 ° по его периметру. Параллакс - это геометрический эффект: на поверхности Земли мы смещены от линии, проходящей через центры Земли и Луны, и из-за этого мы можем наблюдать немного (примерно на 1 °) больше вокруг Луны, когда она находится на наш местный горизонт.[нужна цитата ]
Планеты
Некоторое время считалось, что Меркурий находился в синхронном вращении с Солнцем. Это произошло потому, что всякий раз, когда Меркурий был лучше всего расположен для наблюдения, одна и та же сторона была обращена внутрь. Радиолокационные наблюдения в 1965 году вместо этого продемонстрировали, что Меркурий имеет спин-орбитальный резонанс 3: 2, вращаясь три раза за каждые два оборота вокруг Солнца, что приводит к тому же положению в этих точках наблюдения. Моделирование показало, что Меркурий был захвачен в спин-орбитальное состояние 3: 2 очень рано в своей истории, в течение 20 (а более вероятно, даже 10) миллионов лет после своего образования.[17]
Интервал в 583,92 дня между последовательными близкими подходами Венера на Землю равно 5.001444 венерианских солнечных днях, делая примерно одно и то же лицо видимым с Земли при каждом приближении. Неизвестно, возникли ли эти отношения случайно или в результате какой-то приливной блокировки с Землей.[18]
В экзопланета Проксима Центавра b, обнаруженный в 2016 году, вращается вокруг Проксима Центавра, заблокирован приливом, выражая либо синхронное вращение[19] или спин-орбитальный резонанс 3: 2, как у Меркурия.[20]
Одна из форм гипотетической приливной блокировки экзопланеты находятся планеты глазного яблока, которые в свою очередь делятся на «горячие» и «холодные» планеты глазного яблока.[21][22]
Звезды
близко двойные звезды ожидается, что по всей вселенной будут приливно связаны друг с другом, и внесолнечные планеты которые, как было обнаружено, очень близко вращаются вокруг своих праймериз, также считаются приливно-привязанными к ним. Необычный пример, подтвержденный САМЫЙ, может быть Тау Боэтис, звезда, которая, вероятно, заблокирована своей планетой Тау Boötis b.[23] Если так, то приливная блокировка почти наверняка взаимна.[24][25] Однако, поскольку звезды представляют собой газообразные тела, которые могут вращаться с разной скоростью на разных широтах, приливная блокировка связана с оценкой Тау Бётиса. магнитное поле.[нужна цитата ]
Шкала времени
Оценку времени, в течение которого тело будет заперто приливом, можно получить с помощью следующей формулы:[26]
где
- - начальная скорость вращения, выраженная в радианы в секунду,
- это большая полуось движения спутника вокруг планеты (определяется средним значением перицентр и апоапсис расстояния),
- это момент инерции спутника, где масса спутника и - средний радиус спутника,
- - диссипативная функция спутника,
- это гравитационная постоянная,
- - масса планеты (т. е. вращающегося объекта), и
- это приливный Число любви спутника.
и обычно очень малоизвестны, за исключением Луны, у которой . Для действительно приблизительной оценки принято принимать (возможно, консервативно, давая завышенное время блокировки), и
где
- это плотность спутника
- это сила тяжести на поверхности спутника
- - жесткость спутника. Это можно примерно принять как 3×1010 Н · м−2 для каменистых предметов и 4×109 Н · м−2 для ледяных.
Даже зная размер и плотность спутника, остается много параметров, которые необходимо оценить (особенно ω, Q, и μ), так что любые рассчитанные значения времени блокировки будут неточными, даже с точностью до десяти раз. Кроме того, во время фазы захвата прилива большая полуось могли значительно отличаться от наблюдаемых в настоящее время из-за последующих приливное ускорение, и время блокировки очень чувствительно к этому значению.
Поскольку неопределенность настолько велика, приведенные выше формулы можно упростить, чтобы получить несколько менее громоздкую. Предполагая, что спутник сферический, , и разумно предположить, что один оборот каждые 12 часов в начальном неблокированном состоянии (большинство астероидов имеют периоды вращения от примерно 2 часов до примерно 2 дней)
- [нужна цитата ]
с массами в килограммах, расстояниями в метрах и в ньютонах на квадратный метр; можно примерно принять как 3×1010 Н · м−2 для каменистых предметов и 4×109 Н · м−2 для ледяных.
Существует очень сильная зависимость от большой полуоси. .
Для привязки основного тела к его спутнику, как в случае с Плутоном, параметры спутника и основного тела можно поменять местами.
Один вывод заключается в том, что при прочих равных (такие как и ), большая луна зафиксируется быстрее, чем меньшая луна на том же орбитальном расстоянии от планеты, потому что растет как куб радиуса спутника . Возможный пример этого - система Сатурна, где Гиперион не заблокирован приливом, тогда как больший Япет, который вращается на большем расстоянии, есть. Однако это не совсем однозначно, потому что Гиперион также испытывает сильное вождение с близлежащей дороги. Титан, что делает его вращение хаотичным.
Приведенные выше формулы для шкалы времени синхронизации могут отличаться на порядки, поскольку они игнорируют частотную зависимость . Что еще более важно, они могут быть неприменимы к вязким двойным системам (двойным звездам или двойным астероидам, представляющим собой щебень), потому что спин-орбитальная динамика таких тел определяется в основном их вязкостью, а не жесткостью.[27]
Список известных приливно заблокированных тел
Солнечная система
| Родительский орган | Спутники, заблокированные приливом[28] |
|---|---|
| солнце | Меркурий[29][30][17] (3: 2 спин-орбитальный резонанс) |
| Земля | Луна |
| Марс | Фобос[31] · Деймос[32] |
| Юпитер | Метис · Адрастеа · Амальтея · Бытие · Ио · Европа · Ганимед · Каллисто |
| Сатурн | Сковорода · Атлас · Прометей · Пандора · Эпиметей · Янус · Мимас · Энцелад · Telesto · Тетис · Калипсо · Диона · Рея · Титан · Япет |
| Уран | Миранда · Ариэль · Умбриэль · Титания · Оберон |
| Нептун | Протей · Тритон[31] |
| Плутон | Харон (Сам Плутон привязан к Харону)[11] |
Экстра-солнечный
- Наиболее успешные методы обнаружения экзопланет (транзиты и лучевые скорости) страдают от явной систематической ошибки наблюдений, благоприятствующей обнаружению планет вблизи звезды; таким образом, 85% обнаруженных экзопланет находятся внутри зоны приливного захвата, что затрудняет оценку истинной частоты этого явления.[33] Тау Боэтис как известно, привязан к близкой орбите гигантская планета Тау Boötis b.[23]
Тела могут быть заблокированы
Солнечная система
Основываясь на сравнении вероятного времени, необходимого для привязки тела к его главному элементу, и времени, в течение которого оно находилось на своей нынешней орбите (сравнимо с возрастом Солнечной системы для большинства планетных лун), считается, что ряд лун заблокирован. . Однако их вращения неизвестны или недостаточно известны. Эти:
Вероятно, привязан к Сатурну
Вероятно, привязан к Урану
Вероятно, привязан к Нептуну
Внесолнечный
- Gliese 581c,[34] Глизе 581 г,[35][36] Gliese 581b,[37] и Gliese 581e[38] могут быть привязаны к родительской звезде Gliese 581. Gliese 581d почти наверняка попадает в спин-орбитальный резонанс 2: 1 или 3: 2 с одной и той же звездой.[39]
- Все планеты в TRAPPIST-1 система, вероятно, будет заблокирована приливом.[40][41]
Смотрите также
- Сохранение углового момента
- Гравитационно-градиентная стабилизация - метод стабилизации некоторых искусственных спутников
- Орбитальный резонанс
- Планетарная обитаемость
- Предел Роша
- Синхронная орбита
- Приливное ускорение
использованная литература
- ^ "Когда Земля соединится с Луной?". Вселенная сегодня. 2016-04-12.
- ^ а б Барнс, Рори, изд. (2010). Формирование и эволюция экзопланет. Джон Вили и сыновья. п. 248. ISBN 978-3527408962.
- ^ а б c Heller, R .; Leconte, J .; Барнс, Р. (апрель 2011 г.). «Приливная наклонность потенциально обитаемых планет». Астрономия и астрофизика. 528: 16. arXiv:1101.2156. Bibcode:2011A и A ... 528A..27H. Дои:10.1051/0004-6361/201015809. A27.
- ^ Махони, Т. Дж. (2013). Меркурий. Springer Science & Business Media. ISBN 978-1461479512.
- ^ Льюис, Джон (2012). Физика и химия Солнечной системы. Академическая пресса. С. 242–243. ISBN 978-0323145848.
- ^ Watson, C .; и другие. (Апрель 2006 г.). «Влияние твердотельных моделей земных приливов на координаты GPS и временные ряды тропосферы» (PDF). Письма о геофизических исследованиях. 33 (8): L08306. Bibcode:2006GeoRL..33.8306W. Дои:10.1029 / 2005GL025538.
- ^ де Патер, Имке (2001). Планетарные науки. Кембридж. п. 34. ISBN 978-0521482196.
- ^ Рэй, Р. (15 мая 2001 г.). «Океанские приливы и вращение Земли». Специальное бюро приливов и отливов IERS. Получено 17 марта 2010.
- ^ Murray, C.D .; Дермотт, Стэнли Ф. (1999). Динамика солнечной системы. Издательство Кембриджского университета. п. 184. ISBN 978-0-521-57295-8.
- ^ Дикинсон, Теренс (1993). От Большого взрыва до Планеты X. Камден-Ист, Онтарио: Камден Хаус. С. 79–81. ISBN 978-0-921820-71-0.
- ^ а б Михаэли, Эрез; и другие. (Февраль 2017 г.), «О существовании регулярных и неправильных внешних спутников, вращающихся вокруг системы Плутон – Харон», Астрофизический журнал, 836 (1): 7, arXiv:1506.08818, Bibcode:2017ApJ ... 836 ... 27M, Дои:10.3847 / 1538-4357 / aa52b2, 27
- ^ Correia, Alexandre C.M .; Буэ, Гвенаэль; Ласкар, Жак (январь 2012 г.), «Прокачка эксцентриситета экзопланет с помощью приливного эффекта», Письма в астрофизический журнал, 744 (2): 5, arXiv:1111.5486, Bibcode:2012ApJ ... 744L..23C, Дои:10.1088 / 2041-8205 / 744/2 / L23, L23.
- ^ Макаров, Валерий В. (июнь 2012 г.), «Условия прохождения и захвата планет земной группы в спин-орбитальных резонансах», Астрофизический журнал, 752 (1): 8, arXiv:1110.2658, Bibcode:2012ApJ ... 752 ... 73M, Дои:10.1088 / 0004-637X / 752/1/73, 73.
- ^ Шутц, Бернард (2004-12-04). Гравитация с нуля. Издательство Кембриджского университета. п. 43. ISBN 9780521455060. Получено 24 апреля 2017.
- ^ «7 октября 1959 - Наш первый взгляд на обратную сторону Луны». Вселенная сегодня. 2013-10-07.
- ^ Каин, Фрейзер (2016-04-11). "Когда Земля соединится с Луной?". Вселенная сегодня. Получено 2020-08-03.
- ^ а б Нойэль, Бенуа; Фруар, Жюльен; Макаров, Валерий В. и Ефроимский, Михаил (2014). «Возвращение к спин-орбитальной эволюции Меркурия». Икар. 241: 26–44. arXiv:1307.0136. Bibcode:2014Icar..241 ... 26N. Дои:10.1016 / j.icarus.2014.05.045.
- ^ Золото, т .; Сотер, С. (1969). «Атмосферные приливы и резонансное вращение Венеры». Икар. 11 (3): 356–366. Bibcode:1969Icar ... 11..356G. Дои:10.1016/0019-1035(69)90068-2.
- ^ "Планета, похожая на Землю, вращается вокруг звезды по соседству". Ассошиэйтед Пресс. 2016-08-24. Получено 2016-08-24.
- ^ «Численное моделирование возможных температур поверхности на Проксиме b (синхронное вращение)». ESO. 2016 г.. Получено 24 августа 2016.
- ^ Шон Рэймонд (20 февраля 2015 г.). «Забудьте о« земных »- мы сначала найдем инопланетян на планетах с глазным яблоком». Наутилус. Получено 5 июн 2017.
- ^ Старр, Мишель (5 января 2020 г.). «Планеты с глазным яблоком могут существовать, и они такие же жуткие, как и звучат». ScienceAlert.com. Получено 6 января 2020.
- ^ а б Ширбер, Майкл (2005-05-23). «Смена ролей: планета управляет звездой». space.com. Получено 2018-04-21.
- ^ Сингал, Ашок К. (май 2014 г.). «Жизнь на планете, закрытой от приливов». Информационный бюллетень Planex. 4 (2): 8. arXiv:1405.1025. Bibcode:2014arXiv1405.1025S.
- ^ Уокер, Г. А. Х .; и другие. (2008). «MOST обнаруживает изменчивость на tau Bootis, возможно, вызванную его планетным спутником». Астрономия и астрофизика. 482 (2): 691–697. arXiv:0802.2732. Bibcode:2008A & A ... 482..691 Вт. Дои:10.1051/0004-6361:20078952.
- ^ Б. Гладман; и другие. (1996). "Синхронная синхронизация приливно развивающихся спутников". Икар. 122 (1): 166–192. Bibcode:1996Icar..122..166G. Дои:10.1006 / icar.1996.0117. (См. Страницы 169–170 этой статьи. Здесь цитируется формула (9), взятая из работы С. Дж. Пила, Истории вращения естественных спутников, в Дж. А. Бернс, изд. (1977). Планетарные спутники. Тусон: Университет Аризоны Press. С. 87–112.)
- ^ Ефроимский, М. (2015). «Приливная эволюция астероидных двойных звезд. Управляется вязкостью. Незнание жесткости». Астрономический журнал. 150 (4): 12. arXiv:1506.09157. Bibcode:2015AJ .... 150 ... 98E. Дои:10.1088/0004-6256/150/4/98. 98.
- ^ Нобили, А. М. (апрель 1978 г.), "Вековые эффекты приливного трения на планетно-спутниковые системы Солнечной системы", Луна и планеты, 18 (2): 203–216, Bibcode:1978МиП .... 18..203N, Дои:10.1007 / BF00896743. "Следующие спутники, кажется, вращаются в коротацию: Фобос и Деймос, Амальтея, Ио, Европа, Ганимед, Каллисто, Янус, Мимас, Энцелад, Тетис, Диона, Рея, Титан, Гиперион, Япет, Миранда, Ариэль, Умбриэль, Титания и Оберон. . "
- ^ Пил, С. Дж. (1988), "Вращательная динамика Меркурия и состояние его ядра", Меркурий, University of Arizona Press: 461–493, Bibcode:1988merc.book..461P.
- ^ Ривольдини, А .; и другие. (Сентябрь 2010 г.), «Прошлая и настоящая приливная диссипация Меркурия», Европейский планетарный конгресс 2010: 671, Bibcode:2010epsc.conf..671R.
- ^ а б Коррейя, Александр К. М. (октябрь 2009 г.), "Секулярная эволюция спутника в результате приливного эффекта: приложение к Тритону", Письма в астрофизический журнал, 704 (1): L1 – L4, arXiv:0909.4210, Bibcode:2009ApJ ... 704L ... 1С, Дои:10.1088 / 0004-637X / 704/1 / L1.
- ^ Бернс, Дж. А. (1978), "Динамическая эволюция и происхождение марсианских спутников", Перспективы в астрономии, 22 (2): 193–208, Bibcode:1978ВА ..... 22..193Б, Дои:10.1016/0083-6656(78)90015-6.
- ^ Ф. Дж. Баллестерос; А. Фернандес-Сото; В. Дж. Мартинес (2019). "Название: Погружение в экзопланеты: водные моря самые распространенные?". Астробиология. 19: 642–654. Дои:10.1089 / аст.2017.1720. PMID 30789285.
- ^ Вергано, Дэн (2007-04-25). «Из нашего мира: планета, похожая на Землю». USA Today. Получено 2010-05-25.
- ^ «Астрономы нашли самую похожую на Землю планету на сегодняшний день». Наука, СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ. 29 сентября 2010 г. Архивировано с оригинал 2 октября 2010 г.. Получено 30 сентября, 2010.
- ^ "Gliese 581g - самая похожая на Землю планета из всех, что были открыты". Дейли Телеграф, ВЕЛИКОБРИТАНИЯ. 30 сентября 2010 г. Архивировано с оригинал 2 октября 2010 г.. Получено 30 сентября, 2010.
- ^ «Глизе 581». Открыть каталог Exoplanet. Получено 16 мая 2019.
- ^ «Глизе 581». Энциклопедия Британника. Получено 16 мая 2019.
- ^ Макаров, В. В .; Бергеа, К. и Ефроимски, М. (2012). "Динамическая эволюция и спин-орбитальные резонансы потенциально обитаемых экзопланет: случай GJ 581d". Астрофизический журнал. 761 (2): 83. arXiv:1208.0814. Bibcode:2012ApJ ... 761 ... 83M. Дои:10.1088 / 0004-637X / 761/2/83. 83.
- ^ «Телескоп НАСА обнаружил самую большую партию планет размером с Землю и обитаемых зон вокруг одной звезды» (Пресс-релиз). НАСА. 22 февраля 2017.
- ^ Гиллон, Микаэль; Triaud, Amaury H.M.J .; Демори, Брис-Оливье; Jehin, Emmanuël; Агол, Эрик; Колода, Кэтрин М .; Lederer, Susan M .; де Вит, Жюльен; Бурданов, Артем (23.02.2017). «Семь планет земной группы с умеренным климатом вокруг ближайшей ультрахолодной карликовой звезды TRAPPIST-1». Природа. 542 (7642): 456–460. arXiv:1703.01424. Bibcode:2017Натура.542..456Г. Дои:10.1038 / природа21360. ISSN 0028-0836. ЧВК 5330437. PMID 28230125.