Средняя аномалия - Википедия - Mean anomaly

Площадь выметания за единицу времени объектом в эллиптическая орбита, и воображаемым объектом в круговая орбита (с таким же орбитальным периодом). Обе модели охватывают равные площади за одинаковое время, но угловая скорость движения меняется для эллиптической орбиты и постоянна для круговой орбиты. Показаны средняя аномалия и истинная аномалия за две единицы времени. (Обратите внимание, что для визуальной простоты схематически изображена неперекрывающаяся круговая орбита, таким образом, эта круговая орбита с одинаковым периодом обращения не показана в истинном масштабе с этой эллиптической орбитой: чтобы масштаб был истинным для двух орбит с равным периодом, эти орбиты должен пересекаться.)

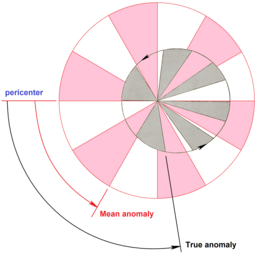
В небесная механика, то средняя аномалия это доля эллиптическая орбита период, прошедший с момента прохождения орбитального тела перицентр, выраженный как угол который можно использовать при вычислении положения этого тела в классическом проблема двух тел. Это угловое расстояние от перицентр которое было бы у фиктивного тела, если бы оно двигалось в круговая орбита, с постоянным скорость, В то же самое орбитальный период как реальное тело на его эллиптической орбите.^[1]^[2]

Определение

Определять Т как время, необходимое конкретному телу для завершения одного витка. Во время Т, то радиус-вектор выметает 2 $π$ радианы или 360 °. Средняя скорость развертки, п, затем

{ displaystyle n = { frac {2 pi} {T}} = { frac {360 ^ { circ}} {T}},}

который называется среднее угловое движение тела с размерами в радианах в единицу времени или градусах в единицу времени.

Определять $τ$ как время, когда тело находится в перицентре. Из приведенных выше определений новое количество, M, то средняя аномалия можно определить

{ Displaystyle М = N (т- тау),}

что дает угловое расстояние от перицентра в произвольный момент времени т,^[3] с размерами в радианах или градусах.

Поскольку скорость увеличения, п, является постоянным средним, средняя аномалия увеличивается равномерно (линейно) от 0 до 2 $π$ радиан или от 0 ° до 360 ° на каждом витке. Он равен 0, когда тело находится в перицентре, $π$ радиан (180 °) при апоцентр, и 2 $π$ радиан (360 °) после одного полного оборота.^[4] Если средняя аномалия известна в любой данный момент, ее можно рассчитать в любой более поздний (или предыдущий) момент, просто добавляя (или вычитая) п δt куда δt представляет разницу во времени.

Средняя аномалия не измеряет угол между какими-либо физическими объектами. Это просто удобная единообразная мера того, как далеко продвинулось тело по своей орбите от перицентра. Средняя аномалия - это один из трех угловых параметров (известных исторически как «аномалии»), которые определяют положение на орбите, два других - это эксцентрическая аномалия и истинная аномалия.

Формулы

Средняя аномалия M можно вычислить из эксцентрическая аномалия E и эксцентриситет е с Уравнение Кеплера:

{ displaystyle M = E-e sin E.}

Средняя аномалия также часто рассматривается как

{ Displaystyle М = М_ {0} + п влево (т-т_ {0} вправо),}

куда M₀ это средняя аномалия в эпоху и т₀ это эпоха, эталонное время, к которому орбитальные элементы упомянуты, которые могут совпадать, а могут и не совпадать с $τ$ , время прохождения перицентра. Классический метод определения положения объекта на эллиптической орбите из набора орбитальных элементов состоит в том, чтобы вычислить среднюю аномалию по этому уравнению, а затем решить уравнение Кеплера для эксцентрической аномалии.

Определять ϖ как долгота перицентра, Угловое расстояние перицентра от опорного направления. Определять $л$ как средняя долгота, Угловое расстояние тела от того же опорного направления, предполагая, что она двигается с равномерным угловым движением как со средней аномалией. Таким образом, средняя аномалия также^[5]

{ displaystyle M = l- varpi.}

Среднее угловое движение также может быть выражено,

{ displaystyle n = { sqrt { frac { mu} {a ^ {3}}}},}

куда μ это гравитационный параметр который меняется в зависимости от массы объектов, и а это большая полуось орбиты. Затем средняя аномалия может быть расширена,

{ displaystyle M = { sqrt { frac { mu} {a ^ {3}}}} (t- tau),}

и здесь средняя аномалия представляет собой равномерное угловое движение по окружности радиуса а.^[6]

Средняя аномалия может быть выражена как расширение серии из эксцентриситет е и истинная аномалия $ν$ ,^[7]

{ displaystyle M = nu -2e sin nu + left ({ frac {3} {4}} e ^ {2} + { frac {1} {8}} e ^ {4} right ) sin 2 nu - { frac {1} {3}} e ^ {3} sin 3 nu + { frac {5} {32}} e ^ {4} sin 4 nu + cdots}

Аналогичная формула дает истинную аномалию непосредственно в терминах средней аномалии:^[8]

{ displaystyle nu = M + left (2e - { frac {1} {4}} e ^ {3} right) sin M + { frac {5} {4}} e ^ {2} sin 2M + { frac {13} {12}} e ^ {3} sin 3M + cdots}

Смотрите также

внешняя ссылка

Запись в глоссарии аномалия, означает в Военно-морской обсерватории США Астрономический альманах онлайн

[1] Монтенбрюк, Оливер (1989). Практические расчеты эфемерид. Springer-Verlag. п.44. ISBN 0-387-50704-3.

[2] Миус, Жан (1991). Астрономические алгоритмы. Willmann-Bell, Inc., Ричмонд, Вирджиния. п.182. ISBN 0-943396-35-2.

[3] Смарт, У. М. (1977). Учебник по сферической астрономии (шестое изд.). Издательство Кембриджского университета, Кембридж. п. 113. ISBN 0-521-29180-1.

[4] Meeus (1991), стр. 183

[5] Смарт (1977), стр. 122

[6] Валладо, Дэвид А. (2001). Основы астродинамики и приложений (второе изд.). Эль-Сегундо, Калифорния: Microcosm Press. С. 53–54. ISBN 1-881883-12-4.

[7] Смарт, У. М. (1953). Небесная механика. Longmans, Green and Co., Лондон. п. 38.

[8] Рой, А. Э. (1988). Орбитальное движение (1-е изд.). Бристоль, Великобритания; Филадельфия, Пенсильвания: А. Хильгер. ISBN 0852743602.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Средняя аномалия - Википедия - Mean anomaly

Содержание

Определение

Формулы

Смотрите также

Рекомендации

внешняя ссылка