Аргумент ведра - Википедия - Bucket argument

Исаак Ньютон вращается аргумент ведра (также известный как Ведро Ньютона) был разработан, чтобы продемонстрировать, что истинное вращательное движение не может быть определено как относительное вращение тела по отношению к непосредственно окружающим телам. Это один из пяти аргументы из «свойств, причин и следствий» «истинного движения и покоя», которые подтверждают его утверждение, что в целом истинное движение и покой не могут быть определены как особые случаи движения или покоя относительный другим органам, но вместо этого может быть определено только ссылкой на абсолютное пространство. В качестве альтернативы эти эксперименты обеспечивают Рабочее определение из того, что имеется в виду под "абсолютное вращение ", и не претендую на решение вопроса" ротации относительно Какие?"^[1] Общая теория относительности обходится без абсолютного пространства и физики, причина которой является внешней по отношению к системе, с концепцией геодезические из пространство-время.^[2]

Фон

Эти аргументы и обсуждение различий между абсолютным и относительным временем, пространством, местом и движением приводятся в схолии в конце разделов Определений в Книге I работы Ньютона. Математические основы естественной философии (1687) (не путать с Общий Схолиум в конце книги III), который установил основы классическая механика и представил свой закон всемирного тяготения, что дало первое количественно адекватное динамическое объяснение планетарное движение.^[3]

Несмотря на то, что они придерживаются принципа прямолинейности инерция и признание кинематической относительности видимого движения (которая лежит в основе Птолемеев или Коперниканец система верна), натурфилософы семнадцатого века продолжали рассматривать истинное движение и покой как физически отдельные дескрипторы отдельного тела. Доминирующая точка зрения, против которой выступал Ньютон, была разработана Рене Декарт, и был поддержан (частично) Готфрид Лейбниц. Он считал, что пустое пространство является метафизической невозможностью, потому что пространство есть не что иное, как расширение материи, или, другими словами, когда кто-то говорит о пространстве между вещами, он фактически ссылается на отношения, которые существуют между этими вещами, а не какой-то сущности, стоящей между ними.^[4][5] В соответствии с вышеприведенным пониманием, любое утверждение о движении тела сводится к описанию во времени, в котором рассматриваемое тело находится в точке t₁ найдены в окрестностях одной группы «знаковых» тел и в некоторый t₂ находится в непосредственной близости от какого-либо другого «ориентирующего» тела или тел.^[6][7]

Обнаружение вращения: красные флажки появляются на гибких рычагах, когда любой объект действительно вращается. A: Центральный объект вращается. B: внешнее кольцо вращается, но в противоположном направлении. C: Оба вращаются, но в противоположных направлениях. D: Оба заблокированы вместе и вращаются в одном направлении.

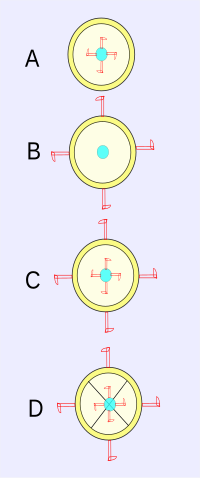
Декарт признал, что существует реальная разница между ситуацией, в которой тело с подвижными частями, первоначально находившимся в состоянии покоя относительно окружающего кольца, само ускоряется до определенной угловой скорости относительно кольца, и другой ситуацией в окружающее кольцо получило противоположное ускорение по отношению к центральному объекту. Что касается только центрального объекта и окружающего кольца, движения будут неотличимы друг от друга, если предположить, что и центральный объект, и окружающее кольцо являются абсолютно твердыми объектами. Однако, если бы ни центральный объект, ни окружающее кольцо не были бы абсолютно жесткими, тогда части одного или обоих из них имели бы тенденцию вылетать из оси вращения.

По случайным причинам, связанным с Инквизиция Декарт говорил о движении как об абсолютном, так и относительном.^{[8][неудачная проверка ]}

К концу 19 века утверждение, что все движение относительно был повторно представлен, в частности Эрнст Мах (1883).^[9][10]

Когда, соответственно, мы говорим, что тело сохраняет неизменными свое направление и скорость в космосе, наше утверждение - не что иное, как сокращенная ссылка на вся вселенная.

— Эрнст Мах; как цитирует Чуфолини и Уиллер: Гравитация и инерция, п. 387

Аргумент

Ньютон обсуждает ведро (латинский: ситуация ) наполненный воды висит на шнурке.^[11] Если шнур плотно намотан на себя, а затем ведро отпущено, оно начинает быстро вращаться не только по отношению к экспериментатору, но и по отношению к содержащейся в нем воде. (Эта ситуация соответствует диаграмме B выше.)

Хотя относительное движение на этом этапе наибольшее, поверхность воды остается плоской, что указывает на то, что части воды не имеют тенденции отклоняться от оси относительного движения, несмотря на близость к ведру. В конце концов, по мере того, как шнур продолжает разматываться, поверхность воды принимает вогнутую форму, поскольку она приобретает движение ведра, вращающегося относительно экспериментатора. Эта вогнутая форма показывает, что вода вращается, несмотря на то, что вода находится в состоянии покоя относительно ведра. Другими словами, это не относительное движение ведра и воды, которое вызывает вогнутость воды, вопреки идее, что движения могут быть только относительными и что абсолютного движения не существует. (Эта ситуация соответствует диаграмме D.) Возможно, вогнутость воды показывает вращение относительно что-то другое: сказать абсолютное пространство? Ньютон говорит: «Можно узнать и измерить истинное и абсолютное круговое движение воды».^[12]

В переводе Эндрю Мотта 1846 года слов Ньютона:^[13]

Если сосуд, подвешенный на длинном шнуре, так часто поворачивают, что шнур сильно перекручивается, затем наполняется водой и удерживается вместе с водой в покое; после того, как внезапное действие другой силы поворачивается в противоположном направлении, и пока шнур раскручивается, судно продолжает некоторое время это движение; поверхность воды сначала будет ровной, как до того, как судно пошло в движение; но судно, постепенно сообщая о своем движении воде, заставит его разумно вращаться, постепенно отступая и поднимаясь по сторонам судна, образуя вогнутую фигуру ... Этот подъем воды показывает свое стремление отойти от оси своего движения; и истинное и абсолютное круговое движение воды, которое здесь прямо противоположно относительному, обнаруживает себя и может быть измерено этим усилием. ... И поэтому это усилие не зависит от какого-либо перемещения воды относительно окружающих тел, и истинное круговое движение не может быть определено таким перемещением. ...; но относительные движения ... совершенно лишены какого-либо реального эффекта. ... Действительно, очень трудно обнаружить и эффективно отличить истинные движения отдельных тел от видимых; потому что части этого неподвижного пространства, в которых совершаются эти движения, никоим образом не подпадают под наблюдение наших органов чувств.

— Исаак Ньютон; Principia, Книга 1: Scholium

Аргумент, что движение является абсолютным, а не относительным, является неполным, поскольку он ограничивает участников, имеющих отношение к эксперименту, только ведром и водой, ограничение, которое не было установлено. Фактически, вогнутость воды явно связана с гравитационным притяжением, и, следовательно, Земля также является его участником. Вот критика Маха, утверждающего, что устанавливается только относительное движение:^[14]

Эксперимент Ньютона с вращающимся сосудом с водой просто информирует нас о том, что относительное вращение воды по отношению к сторонам сосуда не создает заметных центробежных сил, но что такие силы создаются его относительным вращением по отношению к массе Земли. и другие небесные тела.

— Эрнст Мах, как цитирует Л. Букио в Лейбниц, п. 104

В статье обсуждается степень интеграции гипотезы Маха в общую теорию относительности. Принцип маха; Принято считать, что общая теория относительности не совсем махистская.

Все наблюдатели сходятся во мнении, что поверхность вращающейся воды изогнута. Однако объяснение этой кривизны включает центробежную силу для всех наблюдателей, за исключением действительно неподвижного наблюдателя, который обнаруживает, что кривизна соответствует скорости вращения воды, когда они ее наблюдают, без необходимости в дополнительной центробежной силе. Таким образом, можно идентифицировать неподвижную раму, и нет необходимости спрашивать «Стационарная относительно чего?»:

Исходный вопрос: "относительно какой системы отсчета действуют законы движения?" оказывается неправильно поставленным. Для законов движения по существу определять класс систем отсчета и (в принципе) порядок их построения.^[15]

Дополнительный мысленный эксперимент с той же целью определения возникновения абсолютного вращения также был предложен Ньютоном: пример наблюдения двух идентичных сфер, вращающихся вокруг своего центра тяжести и связанных веревкой. Появление натяжения в струне указывает на абсолютное вращение; видеть Вращающиеся сферы.

Детальный анализ

Интерфейс двух несмешиваемый жидкости, вращающиеся вокруг вертикальной оси, представляют собой открывающийся вверх круговой параболоид.

Исторический интерес эксперимента с вращающимся ведром заключается в его полезности, поскольку он позволяет предположить, что можно обнаружить абсолютное вращение, наблюдая за формой поверхности воды. Однако можно задаться вопросом, как ротация вызывает это изменение. Ниже приведены два подхода к пониманию вогнутости поверхности вращающейся воды в ведре.

Силовая диаграмма для элемента водной поверхности в совместно вращающейся раме. Вершина: Радиальный разрез и выбранная точка на поверхности воды; вода, вращающаяся в одном направлении рама и радиальное сечение имеют постоянную угловую скорость вращения, задаваемую вектором Ω. Нижний: Диаграмма сил в выбранной точке на поверхности. Наклон поверхности регулируется, чтобы сумма всех трех сил равнялась нулю.

Законы движения Ньютона

Форму поверхности вращающейся жидкости в ведре можно определить с помощью законов Ньютона для различных сил, действующих на элемент поверхности. Например, см. Knudsen and Hjorth.^[16] Анализ начинается с диаграммы свободного тела в совместно вращающейся системе координат, где вода кажется неподвижной. Высота воды час = час(р) является функцией радиального расстояния р от оси вращения Ω, и цель состоит в том, чтобы определить эту функцию. Показано, что на элемент объема воды на поверхности действуют три силы: вертикальная сила, вызванная силой тяжести. F_грамм, горизонтальная центробежная сила, направленная радиально наружу F_Cfgl, а сила, нормальная к поверхности воды F_п за счет остатка воды, окружающей выбранный элемент поверхности. Известно, что сила, создаваемая окружающей водой, нормальна к поверхности воды, потому что жидкость в равновесии не может поддерживать напряжения сдвига.^[17] Процитируем Энтони и Брэкетта:^[18]

Поверхность жидкости однородной плотности ... в состоянии покоя перпендикулярна силовым линиям; ведь если бы это было не так, сила в точке на поверхности могла бы быть разделена на две составляющие: одна перпендикулярная, а другая касательная к поверхности. Но исходя из природы жидкости, тангенциальная сила вызывает движение жидкости, что противоречит утверждению, что жидкость находится в состоянии покоя.

— Уильям Арнольд Энтони и Сайрус Фогг Брэкетт: Элементарный учебник физики, п. 127

Более того, поскольку элемент воды не движется, сумма всех трех сил должна быть равна нулю. Если суммировать до нуля, сила воды должна быть направлена ​​противоположно сумме центробежной и гравитационной сил, что означает, что поверхность воды должна регулироваться таким образом, чтобы ее нормаль указывала в этом направлении. (Очень похожая проблема - конструкция наклонный поворот, где угол поворота настроен таким образом, чтобы автомобиль не съехал с дороги. Аналогия в случае вращающегося ведра состоит в том, что элемент водной поверхности будет «скользить» вверх или вниз по поверхности, если нормаль к поверхности не совпадает с вектором равнодействующим, образованным векторное сложение F_грамм + F_Cfgl.)

В качестве р увеличивается, центробежная сила увеличивается по соотношению (уравнения записываются на единицу массы):

${ Displaystyle F _ { mathrm {Cfgl}} = м { mathit { Omega}} ^ {2} г ,}$

куда Ω - постоянная скорость вращения воды. Гравитационная сила не меняется при

${ Displaystyle F _ { mathrm {g}} = мг ,}$

куда грамм это ускорение силы тяжести. Эти две силы складываются, чтобы получить равнодействующую под углом φ от вертикали, заданной

${ displaystyle tan varphi = { frac {F _ { mathrm {Cfgl}}} {F _ { mathrm {g}}}} = { frac {{ mathit { Omega}} ^ {2} r }{грамм}} ,}$

который явно становится больше при р увеличивается. Чтобы гарантировать, что эта результирующая нормаль к поверхности воды и, следовательно, может быть эффективно нейтрализована силой воды внизу, нормаль к поверхности должна иметь такой же угол, то есть

${ displaystyle tan varphi = { frac { mathrm {d} h} { mathrm {d} r}} ,}$

приводящее к обыкновенному дифференциальному уравнению для формы поверхности:

${ displaystyle { frac { mathrm {d} h} { mathrm {d} r}} = { frac {{ mathit { Omega}} ^ {2} r} {g}} ,}$

или, интегрируя:

${ displaystyle h (r) = h (0) + { frac {1} {2g}} left ({ mathit { Omega}} r right) ^ {2} ,}$

куда час(0) - высота воды на р = 0. Другими словами, поверхность воды параболическая в зависимости от радиуса.

Потенциальная энергия

Форму поверхности воды можно найти другим, очень интуитивным способом, используя интересную идею потенциальная энергия связанная с центробежной силой в совместно вращающейся системе отсчета. В системе отсчета, равномерно вращающейся с угловой скоростью Ω, фиктивная центробежная сила равна консервативный и имеет потенциальную энергию вида:^[19][20]

${ displaystyle {U} _ { mathrm {Cfgl}} = - { frac {1} {2}} m Omega ^ {2} r ^ {2} ,}$

куда р - радиус от оси вращения. Этот результат можно проверить, взяв градиент потенциала для получения радиально направленной наружу силы:

${ displaystyle F _ { mathrm {Cfgl}} = - { frac { partial} { partial r}} {U} _ { mathrm {Cfgl}}}$ ${ Displaystyle = м Омега ^ {2} г .}$

Значение потенциальной энергии состоит в том, что перемещение пробного тела от большего радиуса к меньшему включает в себя выполнение работай против центробежной силы.

Потенциальная энергия полезна, например, для понимания вогнутости поверхности воды во вращающемся ведре. Обратите внимание, что на равновесие поверхность принимает такую ​​форму, что элемент объема в любом месте на ее поверхности имеет такую ​​же потенциальную энергию, как и в любом другом месте. Таким образом, ни один элемент воды на поверхности не имеет никакого стимула менять положение, потому что все положения эквивалентны по энергии. То есть достигается равновесие. С другой стороны, если бы на поверхности были области с более низкой доступной энергией, вода, занимающая участки поверхности с более высокой потенциальной энергией, сместилась бы, чтобы занять эти места с более низкой энергией, поскольку в идеальной жидкости нет препятствий для бокового движения.

Мы можем представить себе, как намеренно нарушаем эту ситуацию равновесия, каким-то моментом изменяя форму поверхности воды, чтобы она отличалась от поверхности с равной энергией. Это изменение формы не будет стабильным, и вода не останется в нашей искусственно созданной форме, а будет переходить в временное исследование множества форм до тех пор, пока не появятся неидеальные силы трения, возникающие в результате плескания, либо о стороны ведра, либо от воды. Неидеальный характер жидкости погасил колебания, и вода приняла равновесную форму.

Чтобы увидеть в действии принцип равной энергии поверхности, представьте, что скорость вращения ковша постепенно увеличивается с нуля. Поверхность воды сначала плоская и, очевидно, поверхность с одинаковой потенциальной энергией, потому что все точки на поверхности находятся на одинаковой высоте в гравитационном поле, действующем на воду. Однако при некоторой небольшой угловой скорости вращения элемент поверхностной воды может достигать более низкой потенциальной энергии, перемещаясь наружу под действием центробежной силы. Поскольку вода несжимаема и должна оставаться в пределах ковша, это движение наружу увеличивает глубину воды на большем радиусе, увеличивает высоту поверхности на большем радиусе и опускает ее на меньшем радиусе. Поверхность воды становится слегка вогнутой, в результате чего потенциальная энергия воды на большем радиусе увеличивается за счет работы, выполняемой против силы тяжести для достижения большей высоты. По мере увеличения высоты воды движение к периферии перестает быть выгодным, потому что снижение потенциальной энергии от работы с центробежной силой уравновешивается увеличением энергии, работающей против силы тяжести. Таким образом, при заданной угловой скорости вращения вогнутая поверхность представляет собой стабильную ситуацию, и чем быстрее вращается, тем более вогнута эта поверхность. Если вращение прекращается, энергия, накопленная при формировании вогнутой поверхности, должна рассеиваться, например, за счет трения, прежде чем равновесная плоская поверхность будет восстановлена.

Чтобы реализовать поверхность с постоянной потенциальной энергией количественно, пусть высота воды будет ${ Displaystyle ч (г) ,}$: тогда потенциальная энергия силы тяжести на единицу массы равна ${ displaystyle gh (r) }$ а полная потенциальная энергия на единицу массы на поверхности равна

${ displaystyle {U} = {U} _ {0} + gh (r) - { frac {1} {2}} Omega ^ {2} r ^ {2} ,}$

с ${ displaystyle {U} _ {0}}$ уровень фоновой энергии не зависит от р. В статической ситуации (отсутствие движения жидкости во вращающейся раме) эта энергия постоянна и не зависит от положения. р. Требуя постоянства энергии, получаем параболический форма:

${ displaystyle h (r) = { frac { Omega ^ {2}} {2g}} r ^ {2} + h (0) ,}$

куда ч (0) высота на р = 0 (ось). См. Рисунки 1 и 2.

Принцип работы центрифуга также может быть просто понято в терминах этого выражения для потенциальной энергии, которое показывает, что это выгодно с энергетической точки зрения, когда объем, далекий от оси вращения, занят более тяжелым веществом.

Смотрите также

Рекомендации

дальнейшее чтение

• Брайан Грин (2004). «Глава 2, Вселенная и ведро». Ткань космоса: пространство, время и фактура реальности. А А Кнопф. ISBN  0-375-41288-3.
• Изотропия космический фон это еще один показатель того, что Вселенная не вращается. Видеть:
  • Р. Б. Партридж (1995). 3 K: космическое микроволновое фоновое излучение. Издательство Кембриджского университета. С. 279–280. ISBN  0-521-35254-1.
  • Д. Линден-Белл (1996). Релятивистская астрофизика (Игорь Дмитриевич Новиков, Бернар Жан Трефор Джонс, Драза Маркович (редакторы) под ред.). п. 167. ISBN  0-521-62113-5.
  • Ральф А. Альфер и Роберт Херман (1975). Космология большого взрыва и космическое излучение черного тела (в Proc. Являюсь. Фил. Soc. т. 119, нет. 5 (1975) изд.). С. 325–348. ISBN  9781422371077.

внешняя ссылка

• Взгляды Ньютона на пространство, время и движение из Стэнфордской энциклопедии философии, статья Роберта Ринасевича. В конце статьи обсуждается потеря мелких различий в переводах по сравнению с оригинальным латинским текстом.
• Жизнь и философия Лейбница см. раздел о Пространство, время и неразличимое поскольку Лейбниц возражает против идеи пространства, действующего как причинный фактор.
• Ведро Ньютона Интерактивный апплет, иллюстрирующий форму воды, и прикрепленный файл PDF с математическим выводом более полной модели формы воды, чем приведено в этой статье.