Эффект Саньяка - Sagnac effect

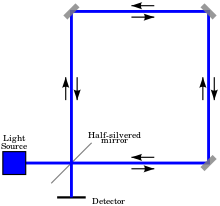
Рис. 1. Схематическое изображение интерферометра Саньяка.

В Эффект Саньяка, также называется Саньяк интерференция, названный в честь французского физика Жорж Саньяк, это явление, встречающееся в интерферометрия что вызвано вращение. Эффект Саньяка проявляется в установке, называемой кольцевым интерферометром. Луч света разделяется, и два луча движутся по одному и тому же пути, но в противоположных направлениях. По возвращении в пункт въезда два световых луча могут покинуть кольцо и пройти вмешательство. Относительные фазы двух выходящих лучей и, следовательно, положение интерференционных полос сдвигаются в соответствии с угловая скорость аппарата. Другими словами, когда интерферометр покоится относительно невращающаяся рама свету требуется одинаковое количество времени, чтобы пересечь кольцо в любом направлении. Однако, когда система интерферометра вращается, один луч света проходит более длинный путь, чем другой, чтобы замкнуть один контур механической рамы, и поэтому требуется больше времени, что приводит к разности фаз между двумя лучами. Это расположение также называется Интерферометр Саньяка. Жорж Саньяк поставил этот эксперимент, чтобы доказать существование эфир что Эйнштейн специальная теория относительности выбросил.[1][2]

А подвес установленный механический гироскоп остается направленным в том же направлении после раскрутки и, таким образом, может использоваться в качестве ориентира вращения для инерциальная навигационная система. С развитием так называемых лазерные гироскопы и волоконно-оптические гироскопы основанный на эффекте Саньяка, объемный механический гироскоп заменяется на устройство без движущихся частей во многих современных инерциальных навигационных системах, однако принципы, лежащие в основе этих двух устройств, различны. Обычный гироскоп основан на принципе сохранение углового момента тогда как чувствительность кольцевого интерферометра к вращению возникает из-за инвариантности скорость света для всех инерциальные системы отсчета.

Описание и работа

Рисунок 2. A направленная волна Интерферометр Саньяка, или волоконно-оптический гироскоп, может быть реализовано с помощью оптоволокно в одну или несколько петель.

Обычно используются три или более зеркала, так что встречные световые лучи проходят по замкнутому пути, например, треугольнику или квадрату (рис. 1). волоконная оптика может использоваться для направления света по замкнутому пути (рис. 2). Если платформа, на которой установлен кольцевой интерферометр, вращается, интерференционные полосы смещены по сравнению с их положением, когда платформа не вращается. Величина смещения пропорциональна угловой скорости вращающейся платформы. Ось вращения не обязательно должна находиться внутри замкнутого пространства. Фазовый сдвиг интерференционных полос пропорционален угловой частоте платформы. и задается формулой, первоначально выведенной Саньяком:

где - ориентированная площадь петли и длина волны света.

Эффект является следствием разного времени, которое требуется правому и левому движущимся световым лучам для полного обхода кольца интерферометра. Разница во времени пробега, умноженная на оптическую частоту , определяет разность фаз .

Измеренное таким образом вращение является абсолютное вращение, то есть поворот платформы относительно инерциальная система отсчета.

История эфирных экспериментов

Смотрите также: История специальной теории относительности § Эксперименты Физо и Саньяка

Ранние предложения построить гигантский кольцевой интерферометр для измерения вращения Земли были сделаны Оливер Лодж в 1897 г., а затем Альберт Абрахам Михельсон в 1904 г. Они надеялись, что с таким интерферометром можно будет сделать выбор между идеей стационарного эфир, и эфир, который полностью увлекает Земля. То есть, если бы гипотетический эфир был унесен Землей (или интерферометром), результат был бы отрицательным, в то время как стационарный эфир дал бы положительный результат.[3][4][5]

Эксперимент, проведенный в 1911 г. Франц Харресс, направленный на измерение Сопротивление Френеля света, распространяющегося через движущееся стекло, в 1920 г. Макс фон Лауэ как фактически представляющий эксперимент Саньяка. Не зная об эффекте Саньяка, Харресс осознал наличие «неожиданного смещения» в своих измерениях, но не смог объяснить его причину.[6]

Первое описание эффекта Саньяка в рамках специальной теории относительности было сделано Лауэ в 1911 г.[7][8] за два года до этого Саньяк провел свой эксперимент. Продолжая теоретические работы Михельсона (1904 г.), фон Лауэ ограничился одним инерциальная система отсчета (которую он назвал «действительной» системой отсчета), а в сноске он написал «систему, которая вращается относительно действительной системы. является не действительный ".[7] Предполагая постоянную скорость света , и задав скорость вращения как , он вычислил время распространения одного луча и встречного луча, и, следовательно, получили разницу во времени . Он пришел к выводу, что этот эксперимент с интерферометром действительно даст (если ограничиться членами первого порядка по ) одинаковый положительный результат как для специальной теории относительности, так и для стационарного эфира (последний он назвал «абсолютной теорией» в отношении теории 1895 г. Лоренц ). Он также пришел к выводу, что только полный эфир модели (например, Стокса или Герц ) дало бы отрицательный результат.[7]

На практике первый интерферометрический эксперимент по наблюдению корреляции угловой скорости и фазового сдвига был проведен французским ученым. Жорж Саньяк в 1913 году. Его целью было обнаружение «эффекта относительного движения эфира».[1][2] Саньяк считал, что его результаты являются доказательством существования неподвижного эфира. Однако, как объяснялось выше, Макс фон Лауэ еще в 1911 году показал, что этот эффект согласуется со специальной теорией относительности.[7][8] В отличие от тщательно подготовленных Эксперимент Майкельсона-Морли который был создан, чтобы доказать, что эфирный ветер вызван сопротивлением земли, эксперимент Саньяка не смог доказать этот тип эфирного ветра, потому что универсальный эфир будет одинаково влиять на все части вращающегося света.

Эйнштейн был полностью осведомлен о феномене эффекта Саньяка благодаря более ранним экспериментам Франц Харресс, математически проанализирована в статье Пол Харзер под названием «Перетаскивание света в стекле и аберрации» в 1914 году.[9] Это было опровергнуто Эйнштейном в его статьях «Наблюдение над статьей П. Харцера: перетаскивание света в стекло и аберрация».[10] и «Ответ на ответ П. Харцера».[11] После математических аргументов Эйнштейна в первой статье Эйнштейн ответил: «Как я показал, частота света относительно среды, через которую он распространяется, является решающей для величины k; потому что она определяет скорость света относительно среды. В нашем случае это световой процесс, который по отношению к системе вращающихся призм следует понимать как стационарный процесс. Отсюда следует, что частота света относительно движущихся призм, а также величина k одинаков для всех призм. Это отвергает ответ г-на Харцера ". (1914)

В 1920 году фон Лауэ продолжил свою теоретическую работу 1911 года, описав эксперимент Харресса и показав роль эффекта Саньяка в этом эксперименте.[6] Лауэ сказал, что в эксперименте Харресса (в котором свет проходит через стекло) была вычислимая разница во времени из-за обоих перетаскивание света (что следует из релятивистского сложение скорости в движущихся средах, т.е. в движущемся стекле) и «тот факт, что каждая часть вращающегося аппарата убегает от одного луча, а приближается к другому», то есть эффект Саньяка. Он признал, что этот последний эффект сам по себе может вызвать отклонение во времени и, следовательно, «ускорения, связанные с вращением, никоим образом не влияют на скорость света».[6]

Хотя объяснение Лауэ основано на инерциальных системах отсчета, Поль Ланжевен (1921, 1937) и другие описали тот же эффект, если смотреть из вращающихся систем отсчета (как в специальной, так и в общей теории относительности, см. Родившиеся координаты ). Таким образом, когда эффект Саньяка должен быть описан с точки зрения вращающейся системы координат, можно использовать обычные вращающиеся цилиндрические координаты и применить их к Метрика Минковского, что приводит к так называемой метрике Борна или метрике Ланжевена.[12][13][14] Из этих координат можно получить различное время прихода встречных лучей, эффект, который был продемонстрирован Поль Ланжевен (1921).[15] Или, когда эти координаты используются для вычисления глобальной скорости света во вращающихся кадрах, в зависимости от ориентации получаются разные скорости видимого света - эффект, который был продемонстрирован Ланжевеном в другой статье (1937).[16]

Это не противоречит специальной теории относительности и приведенному выше объяснению фон Лауэ о том, что на скорость света не влияют ускорения. Поскольку эта кажущаяся переменная скорость света во вращающихся системах координат возникает только при использовании вращающихся координат, тогда как если эффект Саньяка описывается с точки зрения внешней инерциальной системы координат, скорость света, конечно, остается постоянной - поэтому эффект Саньяка возникает независимо от того, используются инерциальные координаты (см. формулы в разделе § Теории ниже) или вращающихся координат (см. формулы в разделе § Системы отсчета ниже). То есть специальная теория относительности в своей первоначальной формулировке была адаптирована к инерциальной системе координат, а не к вращающейся системе координат. Альберт Эйнштейн в его статье, вводящей специальную теорию относительности, говорится, что «свет всегда распространяется в пустом пространстве с определенной скоростью c, которая не зависит от состояния движения излучающего тела».[17] Эйнштейн специально заявил, что скорость света постоянна только в вакууме пустого пространства, используя уравнения, которые выполняются только в линейных и параллельных инерциальных системах отсчета. Однако, когда Эйнштейн начал исследовать ускоренные системы отсчета, он заметил, что «принцип постоянства света должен быть изменен» для ускоренных систем отсчета.[18]

Макс фон Лауэ в своей статье 1920 года серьезно рассмотрел влияние Общая теория относительности об эффекте Саньяка, заявив: «Общая теория относительности, конечно, могла бы дать некоторые утверждения об этом, и мы хотим сначала показать, что в соответствии с ней не ожидается никаких заметных влияний ускорения». Он делает сноску относительно дискуссий с немецким физиком: Вильгельм Вена.[6] Причина взглянуть на Общая теория относительности потому что Эйнштейн Общая теория относительности предсказал, что свет будет замедляться в гравитационном поле, поэтому он мог предсказать кривизну света вокруг массивного тела. В общей теории относительности есть принцип эквивалентности который утверждает, что сила тяжести и ускорение эквивалентны. Вращение или ускорение интерферометра создает гравитационный эффект. «Однако есть два разных типа такого [неинерциального] движения; это может быть, например, ускорение по прямой или круговое движение с постоянной скоростью».[19] Кроме того, Ирвин Шапиро в 1964 году объяснил общую теорию относительности, сказав: «Скорость световой волны зависит от силы гравитационного потенциала на ее пути». Это называется Задержка Шапиро.[20] Однако, поскольку гравитационное поле должно быть значительным, Лауэ (1920) пришел к выводу, что более вероятно, что этот эффект является результатом изменения расстояния пути в результате его движения в пространстве.[6] "Луч, движущийся по петле в направлении вращения, должен будет пройти дальше, чем луч, движущийся против направления вращения, потому что в течение периода движения зеркала и детектор будут все (немного) перемещаться в сторону встречно вращающегося луча. и вдали от совместно вращающегося луча. Следовательно, лучи будут достигать детектора в несколько разное время и немного не в фазе, создавая оптические интерференционные «полосы», которые можно наблюдать и измерять »[21]

В 1926 году амбициозный эксперимент по кольцевой интерферометрии был поставлен Альберт Михельсон и Генри Гейл. Цель заключалась в том, чтобы выяснить, влияет ли вращение Земли на распространение света в окрестностях Земли. В Эксперимент Майкельсона – Гейла – Пирсона был очень большим кольцевым интерферометром (периметр 1,9 километра), достаточно большим, чтобы определять угловую скорость Земли. Результатом эксперимента было то, что угловая скорость Земли, измеренная астрономами, была подтверждена с точностью измерения. Кольцевой интерферометр эксперимента Майкельсона – Гейла не калибровался сравнением с внешним эталоном (что было невозможно, поскольку установка была прикреплена к Земле). Из его конструкции можно было вывести, где должна быть центральная интерференционная полоса, если бы сдвиг был нулевым. Измеренный сдвиг составлял 230 частей на 1000, с точностью 5 частей на 1000. Прогнозируемый сдвиг составлял 237 частей на 1000.[22]

Эксперимент Ванга

Модифицированные версии эксперимента Саньяка были сделаны Ван и др.[23] в конфигурациях, аналогичных показанным на рис.3.

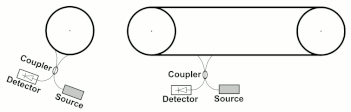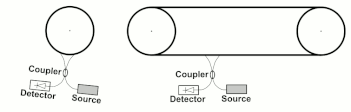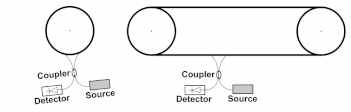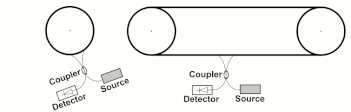
Рис. 3. Жесткий интерферометр Саньяка, показанный слева, и деформируемый интерферометр Ванга, показанный справа.

Интерферометр Ванга не движется как твердое тело, и исходная формула Саньяка не применяется в качестве угловой частоты вращения. не определено. Wang et al. экспериментально подтверждено, что применима обобщенная формула Саньяка.

Релятивистский вывод формулы Саньяка

Рис. 4: Замкнутое оптическое волокно, произвольно перемещающееся в пространстве без растяжения.

Рассмотрим кольцевой интерферометр, в котором два встречных световых луча имеют общий оптический путь, определяемый петлей оптического волокна, см. Рисунок 4. Петля может иметь произвольную форму и может произвольно перемещаться в пространстве. Единственное ограничение - нельзя растягиваться. (Случай кольцевого интерферометра, вращающегося вокруг своего центра в свободном пространстве, восстанавливается, если принять показатель преломления волокна равным 1.)

Рассмотрим небольшой отрезок волокна, длина которого в остальной рамке равна . Временные интервалы, , требуется, чтобы левый и правый движущиеся лучи света пересекали отрезок в системе покоя, совпадают и задаются выражением

Позволять быть длиной этого небольшого сегмента в лабораторной рамке. По релятивистской сокращение длины формула исправить до первого порядка по скорости сегмента. Временные интервалы для прохождения сегмента в лабораторной раме задаются Преобразование Лоренца так как:
исправить до первого порядка по скорости . Как правило, два луча посещают данный сегмент в несколько разное время, но при отсутствии растяжения длина одинаков для обеих балок.

Отсюда следует, что разница во времени завершения цикла для двух лучей составляет

Примечательно, что разница во времени не зависит от показателя преломления. и скорость света в волокне.

Представьте себе экран для просмотра полос, расположенный у источника света (в качестве альтернативы, используйте светоделитель, чтобы направить свет от точки источника на экран). При постоянном источнике света на экране будут формироваться интерференционные полосы со смещением полос, определяемым выражением где первый фактор - частота света. Это дает обобщенную формулу Саньяка[24]

В частном случае, когда волокно движется как твердое тело с угловой частотой , скорость а линейный интеграл можно вычислить в терминах площади контура:
Это дает формулу Саньяка для кольцевых интерферометров произвольной формы и геометрии
Если также допустить растяжение, то восстановится Физо формула интерференции.[24]

Эффект Саньяка стимулировал столетние дискуссии о его значении и интерпретации.[25][26][27] Многие из этих споров вызывают удивление, поскольку эффект прекрасно понимается в контексте специальной теории относительности.

Другие обобщения

Реле импульсов, которое совершает кругосветное путешествие вокруг Земли, проверяя точную синхронизацию, также считается случаем, требующим коррекции эффекта Саньяка. В 1984 году была проведена проверка, в которой участвовали три наземные станции и несколько спутников GPS, с ретрансляторами сигналов, идущих как на восток, так и на запад по всему миру.[28] В случае интерферометра Саньяка мера разницы во времени прихода получается путем создания интерференционных полос и наблюдения за их сдвигом. В случае ретрансляции импульсов по всему миру разница во времени прихода получается непосредственно из фактического времени прибытия импульсов. В обоих случаях механизм разницы во времени прихода один и тот же: эффект Саньяка.

В Эксперимент Хафеле – Китинга также признан аналогом физики эффекта Саньяка.[28] В реальном эксперименте Хафеле – Китинга[29] вид транспорта (дальние перелеты) сам по себе вызывает эффект замедления времени, и для разделения различных вкладов потребовались расчеты. Для (теоретического) случая часов, которые перемещаются настолько медленно, что эффекты замедления времени, возникающие из-за переноса, пренебрежимо малы, разница во времени между часами, когда они возвращаются в начальную точку, будет равна разнице во времени, которая найдена для реле импульсов, которое путешествует по миру: 207 наносекунд.

Практическое использование

Эффект Саньяка используется в современной технике. Одно использование в инерциальные системы наведения. Кольцевые лазерные гироскопы чрезвычайно чувствительны к вращению, что необходимо учитывать, если инерционная система наведения должна возвращать точные результаты. Кольцевой лазер также может обнаруживать звездный день, который также можно назвать «режимом 1». Глобальные навигационные спутниковые системы (GNSS), например GPS, ГЛОНАСС, КОМПАС или Галилео, необходимо учитывать вращение Земли в процедурах использования радиосигналов для синхронизации часов.

Кольцевые лазеры

Дальнейшая информация: Кольцевой лазерный гироскоп
Рис. 6. Схематическое изображение кольцевой лазерной установки.

Волоконно-оптические гироскопы иногда называют «пассивными кольцевыми интерферометрами». Пассивный кольцевой интерферометр использует свет, попадающий в установку извне. Получаемая интерференционная картина представляет собой полосовую картину, а измеряется фазовый сдвиг.

Также возможно построить замкнутый кольцевой интерферометр на основе совершенно другой конструкции. Это называется кольцевой лазер или кольцевой лазерный гироскоп. Свет генерируется и поддерживается за счет включения лазерного возбуждения на пути света.

Чтобы понять, что происходит в резонаторе кольцевого лазера, полезно обсудить физику лазерного процесса в лазерной установке с непрерывной генерацией света. Когда начинается лазерное возбуждение, молекулы внутри резонатора излучают фотоны, но поскольку молекулы имеют тепловую скорость, свет внутри лазерного резонатора сначала представляет собой диапазон частот, соответствующий статистическому распределению скоростей. Процесс стимулированное излучение заставляет одну частоту быстро превосходить другие частоты, и после этого свет становится очень близким к монохроматическому.

Рис. 7. Схематическое изображение сдвига частоты при вращении кольцевого лазерного интерферометра. Как встречный, так и совместно распространяющийся свет проходят 12 циклов своей частоты.

Для простоты предположим, что все испускаемые фотоны испускаются в направлении, параллельном кольцу. Рис. 7 иллюстрирует эффект вращения кольцевого лазера. В линейном лазере целое кратное длины волны соответствует длине резонатора лазера. Это означает, что, путешествуя вперед и назад, лазерный луч проходит через целое число циклы его частоты. То же самое и с кольцевым лазером: количество циклов частоты лазерного излучения одинаково в обоих направлениях. Это качество одинакового количества циклов в обоих направлениях сохраняется при вращении кольцевой лазерной установки. Изображение показывает, что существует сдвиг длины волны (следовательно, сдвиг частоты) таким образом, что количество циклов одинаково в обоих направлениях распространения.

Приведя две частоты лазерного света к интерференции частота биений может быть получен; частота биений - это разница между двумя частотами. Эту частоту биений можно рассматривать как интерференционную картину во времени. (Более знакомые интерференционные полосы интерферометрии представляют собой пространственный узор). Период этой частоты биений линейно пропорционален угловой скорости кольцевого лазера относительно инерционного пространства. Это принцип кольцевой лазерный гироскоп, широко используется в современных инерциальные навигационные системы.

Калибровка нулевой точки

Рис. 8. Красные и синие точки представляют собой встречные фотоны, серые точки - молекулы в резонаторе лазера.

В пассивных кольцевых интерферометрах смещение полосы пропорционально первой производной углового положения; Требуется тщательная калибровка для определения смещения полосы, соответствующего нулевой угловой скорости установки кольцевого интерферометра. С другой стороны, кольцевые лазерные интерферометры не требуют калибровки для определения выходного сигнала, соответствующего нулевой угловой скорости. Кольцевые лазерные интерферометры являются самокалибрующимися. Частота биений будет равна нулю, если и только если установка кольцевого лазера не вращается относительно инерционного пространства.

На рис. 8 показано физическое свойство, обеспечивающее самокалибровку кольцевого лазерного интерферометра. Серые точки представляют молекулы в полости лазера, которые действуют как резонаторы. Вдоль каждого участка кольцевой полости скорость света одинакова в обоих направлениях. Когда кольцевое лазерное устройство вращается, оно вращается относительно этого фона. Другими словами: неизменность скорости света служит эталоном для самокалибровки кольцевого лазерного интерферометра.

Блокировка

Кольцевые лазерные гироскопы страдают от эффекта, известного как «синхронизация» при низких скоростях вращения (менее 100 ° / ч). При очень малых скоростях вращения частоты встречных лазерных мод становятся практически идентичными. В этом случае перекрестные помехи между встречно распространяющимися лучами могут привести к блокировка впрыска, так что стоячая волна «застревает» в предпочтительной фазе, привязывая частоты каждого луча друг к другу, а не реагируя на постепенное вращение.По ротации дизеринг резонатор лазера вперед и назад на небольшой угол с большой скоростью (сотни герц ), блокировка будет происходить только в кратковременных случаях, когда скорость вращения близка к нулю; вызванные таким образом ошибки приблизительно компенсируют друг друга между чередующимися мертвыми периодами.

Волоконно-оптические гироскопы против кольцевые лазерные гироскопы

Волоконно-оптические гироскопы (ВОГ) и кольцевые лазерные гироскопы (RLG) работают, отслеживая разницу во времени распространения между лучами света, движущимися по часовой стрелке и против часовой стрелки по замкнутому оптическому пути. Они значительно различаются по стоимости, надежности, размеру, весу, мощности и другим характеристикам производительности, которые необходимо учитывать при оценке этих различных технологий для конкретного приложения.

RLG требуют точной обработки, использования прецизионных зеркал и сборки в условиях чистой комнаты. Их механические узлы дизеринга несколько увеличивают их вес, но незначительно.[нужна цитата ] RLG могут работать более 100 000 часов при температуре, близкой к комнатной.[нужна цитата ] Их лазеры требуют относительно высокой мощности.[30]

Интерферометрические ВОГ являются полностью твердотельными, не требуют компонентов механического дизеринга, не требуют точной обработки, имеют гибкую геометрию и могут быть сделаны очень маленькими. Они используют многие стандартные компоненты телекоммуникационной отрасли. Кроме того, основные оптические компоненты ВОГ доказали свою эффективность в телекоммуникационной отрасли, а их срок службы измеряется десятилетиями.[31] Однако сборка нескольких оптических компонентов в прецизионный гироскоп обходится дорого. Аналоговые FOG предлагают минимально возможную стоимость, но имеют ограниченную производительность; цифровые ВОГ предлагают широкий динамический диапазон и точную коррекцию масштабного коэффициента, необходимые для строгих приложений.[32] Использование более длинных и больших катушек увеличивает чувствительность за счет большей чувствительности к колебаниям температуры и вибрации.

Интерферометр Саньяка с нулевой площадью и обнаружение гравитационных волн

Топология Саньяка была впервые описана Майкельсоном в 1886 г.[33] который использовал вариант этого интерферометра с четным отражением в повторении Физо эксперимент.[34] Майкельсон отметил чрезвычайную стабильность полос, создаваемых интерферометром этой формы: полосы белого света наблюдались сразу после выравнивания зеркал. В двухлучевых интерферометрах сложно получить полосы белого света, так как две длины пути должны быть согласованы с точностью до пары микрометры (в длина когерентности белого света). Однако, будучи интерферометр с общим трактом, конфигурация Саньяка по своей сути соответствует двум длинам пути. Аналогичным образом Майкельсон заметил, что рисунок полос останется стабильным даже при удерживании зажженной спички ниже оптического пути; в большинстве интерферометров полосы будут сильно смещаться из-за показатель преломления колебания от теплого воздуха над спичкой. Интерферометры Саньяка почти полностью нечувствительны к смещениям зеркал или светоделителя.[35] Эта характеристика топологии Саньяка привела к их использованию в приложениях, требующих исключительно высокой стабильности.

Рис. 9. Интерферометр Саньяка с нулевой площадью.

Сдвиг полосы в интерферометре Саньяка из-за вращения имеет величину, пропорциональную замкнутой области светового пути, и эта область должна быть указана относительно оси вращения. Таким образом, знак площади петли меняется на противоположный, когда петля наматывается в обратном направлении (по или против часовой стрелки). Световой путь, который включает петли в обоих направлениях, поэтому имеет чистую площадь, определяемую разницей между площадями петель по и против часовой стрелки. Частный случай двух равных, но противоположных петель называется нулевая площадь Интерферометр Саньяка. В результате получился интерферометр, демонстрирующий стабильность топологии Саньяка, но нечувствительный к вращению.[36]

В Лазерный интерферометр Гравитационно-волновая обсерватория (LIGO) состояла из двух 4-км Интерферометры Майкельсона – Фабри – Перо, и работал на уровне мощности около 100 Вт мощности лазера на светоделителе. После обновления до Advanced LIGO потребуется несколько киловатт мощности лазера.

Разнообразные конкурирующие оптические системы исследуются на предмет усовершенствования третьего поколения помимо Advanced LIGO.[37] Одно из этих конкурирующих предложений основано на дизайне Саньяка с нулевой площадью. При световом пути, состоящем из двух петель одинаковой площади, но в противоположных направлениях, получается нулевая эффективная площадь, что устраняет эффект Саньяка в его обычном смысле. Несмотря на то, что эта конфигурация нечувствительна к низкочастотному дрейфу зеркала, изменению частоты лазера, дисбалансу отражательной способности между плечами и термически индуцированному двулучепреломлению, эта конфигурация, тем не менее, чувствительна к прохождению гравитационные волны на частотах, представляющих астрономический интерес.[36] Тем не менее, при выборе оптической системы необходимо учитывать множество факторов, и, несмотря на превосходство Саньяка с нулевой площадью в определенных областях, до сих пор нет единого мнения о выборе оптической системы для третьего поколения LIGO.[38][39]

Смотрите также

использованная литература

  1. ^ а б Саньяк, Жорж (1913), "L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromètre en ротационная униформа" [Демонстрация светоносного эфира интерферометром при равномерном вращении ], Comptes Rendus, 157: 708–710
  2. ^ а б Саньяк, Жорж (1913), "Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant" [О доказательстве реальности светоносного эфира экспериментом с вращающимся интерферометром ], Comptes Rendus, 157: 1410–1413
  3. ^ Андерсон, Р .; Bilger, H.R .; Стедман, Г. (1994). «Эффект Саньяка: век интерферометров вращения Земли». Am. J. Phys. 62 (11): 975–985. Bibcode:1994AmJPh..62..975A. Дои:10.1119/1.17656.
  4. ^ Лодж, Оливер (1897). «Эксперименты по отсутствию механической связи между эфиром и материей». Филос. Пер. Р. Соц. 189: 149–166. Bibcode:1897РСПТА.189..149Л. Дои:10.1098 / рста.1897.0006.
  5. ^ Михельсон, А.А. (1904). «Относительное движение Земли и эфира». Философский журнал. 8 (48): 716–719. Дои:10.1080/14786440409463244.
  6. ^ а б c d е Лауэ, Макс фон (1920). "Zum Versuch von F. Harress". Annalen der Physik. 367 (13): 448–463. Bibcode:1920AnP ... 367..448L. Дои:10.1002 / andp.19203671303. Английский перевод: Об эксперименте Ф. Харресса
  7. ^ а б c d Лауэ, Макс фон (1911). "Über einen Versuch zur Optik der bewegten Körper". Münchener Sitzungsberichte: 405–412. Английский перевод: Об эксперименте по оптике движущихся тел.
  8. ^ а б Паули, Вольфганг (1981). Теория относительности. Нью-Йорк: Дувр. ISBN  978-0-486-64152-2.
  9. ^ Список научных публикаций Альберта Эйнштейна
  10. ^ Astronomische Nachrichten, 199, 8–10
  11. ^ Astronomische Nachrichten, 199, 47–48.
  12. ^ Гвидо Рицци; Маттео Лука Руджеро (2003). «Релятивистский эффект Саньяка: два вывода». В Г. Рицци; М.Л. Руджеро (ред.). Относительность во вращающихся кадрах. Дордрехт: Kluwer Academic Publishers. arXiv:gr-qc / 0305084. Bibcode:2003гр.кв ..... 5084р. ISBN  978-0-486-64152-2.
  13. ^ Эшби, Н. (2003). «Относительность в системе глобального позиционирования». Живущий Преподобный Релятив. 6 (1): 1. Bibcode:2003ЛРР ..... 6 .... 1А. Дои:10.12942 / lrr-2003-1. ЧВК  5253894. PMID  28163638. (Открытый доступ)
  14. ^ Л.Д. Ландау, Э.М.Лифшиц, (1962). «Классическая теория поля». 2-е издание, Pergamon Press, стр. 296–297.
  15. ^ Ланжевен, Поль (1921). "Sur la théorie de la relativité et l'expérience de M. Sagnac". Comptes Rendus. 173: 831–834.
  16. ^ Ланжевен, Поль (1937). "Sur l'Expérience de M. Sagnac". Comptes Rendus. 205: 304–306.
  17. ^ Альберт Эйнштейн, 1905, «Об электродинамике движущихся тел». http://www.fourmilab.ch/etexts/einstein/specrel/www/
  18. ^ А. Эйнштейн, «Обобщенная теория относительности», 94; антология «Принцип относительности», А. Эйнштейн и Х. Минковский, Университет Калькутты, 1920 г.
  19. ^ «Общая теория относительности», Льюис Райдер, издательство Кембриджского университета (2009). Стр.7
  20. ^ http://www.physicsdiscussionforum.org/download/file.php?id=250
  21. ^ «Эффект Саньяка».
  22. ^ Майкельсон, Альберт Абрахам; Гейл, Генри Г. (1925). "Эффект Землиs Вращение на скорости света, II ". Астрофизический журнал. 61: 140–145. Bibcode:1925ApJ .... 61..140M. Дои:10.1086/142879.
  23. ^ Wang, R .; Zheng, Y .; Yao, A .; Лэнгли, Д. (2006). «Модифицированный эксперимент Саньяка для измерения разницы во времени прохождения встречных световых лучей в равномерно движущемся волокне». Письма о физике A. 312 (1–2): 7–10. arXiv:физика / 0609222. Bibcode:2003ФЛА..312 .... 7Вт. Дои:10.1016 / S0375-9601 (03) 00575-9. S2CID  699912.
  24. ^ а б Ори, А. (2016). «Обобщенная формула Саньяка-Ванга-Физо». Физический обзор A. 94 (6): 063837. arXiv:1601.01448. Bibcode:2016PhRvA..94f3837O. Дои:10.1103 / Physreva.94.063837. S2CID  119242639.
  25. ^ Стедман, Г. Э. (1997). «Кольцевые лазерные испытания фундаментальной физики и геофизики». Rep. Prog. Phys. 60 (6): 615–688. Bibcode:1997РПФ ... 60..615С. CiteSeerX  10.1.1.128.191. Дои:10.1088/0034-4885/60/6/001.
  26. ^ Малыкин, Г. Б. (2002). «Эффект Саньяка во вращающейся системе отсчета. Релятивистский парадокс Зенона» (PDF). Успехи физики. 45 (8): 907–909. Bibcode:2002PhyU ... 45..907M. Дои:10.1070 / pu2002v045n08abeh001225. Получено 15 февраля 2013.
  27. ^ Тарталья, А .; Руджеро, М. Л. (2004). «Эффект Саньяка и чистая геометрия». arXiv:gr-qc / 0401005.
  28. ^ а б Аллан Д. В., Вайс М. А. и Эшби Н. (1985). «Кругосветный релятивистский эксперимент Саньяка». Наука. 228 (4695): 69–71. Bibcode:1985 Наука ... 228 ... 69А. Дои:10.1126 / science.228.4695.69. PMID  17811569. S2CID  22556404.CS1 maint: несколько имен: список авторов (ссылка на сайт)
  29. ^ Хафеле Дж., Китинг Р. (1972-07-14). «Атомные часы во всем мире: предсказанный релятивистский выигрыш времени». Наука. 177 (4044): 166–168. Bibcode:1972Научный ... 177..166H. Дои:10.1126 / science.177.4044.166. PMID  17779917. S2CID  10067969. Получено 2006-09-18.CS1 maint: несколько имен: список авторов (ссылка на сайт)
  30. ^ Juang, J.-N .; Радхараманан, Р. «Оценка технологии кольцевого лазера и волоконно-оптического гироскопа» (PDF). Получено 15 февраля 2013.
  31. ^ Наполитано, Ф. «Ключевые технологические преимущества волоконно-оптических гироскопов» (PDF). iXSea. Архивировано из оригинал (PDF) 5 марта 2012 г.. Получено 15 февраля 2013.
  32. ^ Udd, E .; Watanabe, S. F .; Кэхилл, Р. Ф. (1986). «Сравнение кольцевой лазерной и волоконно-оптической гироскопической техники». В управляемых оптических структурах Agard в военной среде 14 P (см. N87-13273 04-74. Макдоннелл-Дуглас. Bibcode:1986госм.агар ..... У.
  33. ^ Харихаран, П. (1975). «Саньяк или интерферометр Майкельсона – Саньяка?». Прикладная оптика. 14 (10): 2319_1–2321. Bibcode:1975ApOpt..14.2319H. Дои:10.1364 / AO.14.2319_1. PMID  20155007.
  34. ^ Майкельсон, А.А., Морли, Э.В. (1886). «Влияние движения среды на скорость света». Am. J. Sci. 31 (185): 377–386. Bibcode:1886AmJS ... 31..377M. Дои:10.2475 / ajs.s3-31.185.377. S2CID  131116577.
  35. ^ Харихаран, П. (2003). Оптическая интерферометрия (Второе изд.). Академическая пресса. С. 28–29. ISBN  978-0-12-311630-7.
  36. ^ а б Вс, K-X .; Fejer, M.M .; Gustafson, E .; Байер Р.Л. (1996). «Интерферометр Саньяка для обнаружения гравитационных волн» (PDF). Письма с физическими проверками. 76 (17): 3053–3056. Bibcode:1996ПхРвЛ..76.3053С. Дои:10.1103 / PhysRevLett.76.3053. PMID  10060864. Получено 31 марта 2012.
  37. ^ Punturo, M .; Abernathy, M .; Acernese, F .; Allen, B .; Андерссон, Н .; Arun, K .; Barone, F .; Barr, B .; Барсуглиа, М .; Бекер, М .; Beveridge, N .; Birindelli, S .; Bose, S .; Bosi, L .; Braccini, S .; Bradaschia, C .; Булик, Т .; Calloni, E .; Cella, G .; Chassande Mottin, E .; Chelkowski, S .; Chincarini, A .; Clark, J .; Coccia, E .; Colacino, C .; Colas, J .; Камминг, А .; Cunningham, L .; Cuoco, E .; и другие. (2010). «Третье поколение обсерваторий гравитационных волн и их научные достижения». Классическая и квантовая гравитация. 27 (8): 084007. Bibcode:2010CQGra..27х4007P. Дои:10.1088/0264-9381/27/8/084007. HDL:11858 / 00-001M-0000-0011-2EAE-2.
  38. ^ Freise, A .; Chelkowski, S .; Hild, S .; Pozzo, W. D .; Perreca, A .; Веккьо, А. (2009). «Тройной интерферометр Майкельсона для детектора гравитационных волн третьего поколения». Классическая и квантовая гравитация. 26 (8): 085012. arXiv:0804.1036. Bibcode:2009CQGra..26h5012F. Дои:10.1088/0264-9381/26/8/085012. S2CID  7535227.
  39. ^ Eberle, T .; Steinlechner, S .; Bauchrowitz, J. R .; Händchen, V .; Vahlbruch, H .; Mehmet, M .; Müller-Ebhardt, H .; Шнабель, Р. (2010). "Квантовое улучшение топологии интерферометра Саньяка с нулевой площадью для обнаружения гравитационных волн". Письма с физическими проверками. 104 (25): 251102. arXiv:1007.0574. Bibcode:2010PhRvL.104y1102E. Дои:10.1103 / PhysRevLett.104.251102. PMID  20867358. S2CID  9929939.

внешние ссылки