Ареальная скорость - Areal velocity
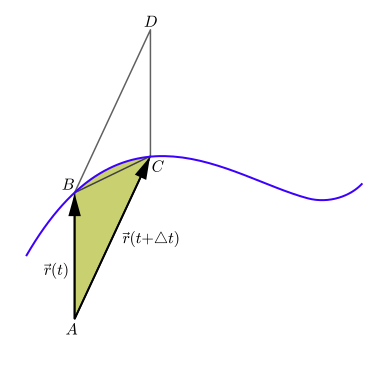
В классическая механика, площадная скорость (также называемый скорость сектора или же секторная скорость) - скорость, с которой площадь уносится частицей при движении по изгиб. На следующем рисунке предположим, что частица движется по синей кривой. В определенное время т, частица находится в точке B, и немного позже, вовремя т + Δт, частица переместилась в точку C. Область, выметаемая частицей, - это зеленая область на рисунке, ограниченная отрезками линии. AB и AC и кривая, по которой движется частица. Площадная скорость равна этой площади, деленной на интервал времени Δт в пределе Δт становится исчезающе маленьким. Это пример псевдовектор (также называемый осевой вектор), направленный перпендикулярно плоскости, содержащей векторы положения и скорости частицы.

Понятие площадной скорости исторически тесно связано с понятием угловой момент. Второй закон Кеплера утверждает, что пространственная скорость планеты с Солнцем, взятым за начало координат, постоянна. Исаак Ньютон был первым ученым, осознавшим динамическое значение второго закона Кеплера. С помощью своих законов движения он доказал в 1684 году, что любая планета, притягиваемая к фиксированному центру, сметает равные площади за равные промежутки времени. К середине 18 века принцип углового момента был открыт постепенно. Даниэль Бернулли и Леонард Эйлер и Патрик д'Арси; Версия принципа д'Арси была сформулирована в терминах охваченной площади. По этой причине принцип углового момента часто упоминался в более ранней литературе по механике как «принцип равных площадей». Поскольку понятие углового момента включает больше, чем просто геометрию, обозначение «принцип равных площадей» было опущено в современных работах.
Связь с угловым моментом
В ситуации, показанной на первом рисунке, область, выметаемая за период времени Δт частицей примерно равна площади треугольника ABC. В качестве Δt стремится к нулю, это почти равенство становится точным, когда предел.
Пусть точка D быть четвертым углом параллелограмма ABDC показано на рисунке, так что векторы AB и AC сложить по правилу параллелограмма до вектора ОБЪЯВЛЕНИЕ. Тогда площадь треугольника ABC половина площади параллелограмма ABDC, а площадь ABDC равна величине перекрестное произведение векторов AB и AC. Эту область также можно рассматривать как вектор с этой величиной, указывающий в направлении, перпендикулярном параллелограмму; этот вектор и есть кросс-произведение:
Следовательно
Площадная скорость - это площадь вектора, деленная на Δт в пределе Δт становится исчезающе маленьким:
Но, - вектор скорости движущейся частицы, так что
С другой стороны, угловой момент частицы равен
а значит, угловой момент равен 2м умножить на площадную скорость.
Сохранение площадной скорости - общее свойство движение центральной силы,[1] и в контексте классической механики эквивалентно сохранению углового момента.
Рекомендации
- Моултон, Ф. Р. (1970) [1914]. Введение в небесную механику. Дувр. ISBN 978-0-486-64687-9.
- Гольдштейн, Х. (1980). Классическая механика (2-е изд.). Эддисон-Уэсли. ISBN 978-0-486-68063-7.
- Кейси, Дж. (2007). «Площадная скорость и угловой момент для неплоских задач в механике элементарных частиц». Американский журнал физики. 75 (8): 677–685. Bibcode:2007AmJPh..75..677C. Дои:10.1119/1.2735630.
- Бракенридж, Дж. Б. (1995). Ключ к динамике Ньютона: проблема Кеплера и принципы. Беркли: Калифорнийский университет Press. Дои:10.1525 / j.ctt1ppn2m. ISBN 978-0-520-20217-7.







