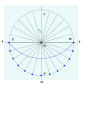
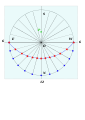
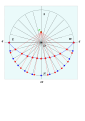
Схема для горизонтальных циферблатов - Schema for horizontal dials

А схема для горизонтальных циферблатов представляет собой набор инструкций, используемых для построения горизонтальных солнечные часы с помощью компас и линейка техники, которые широко использовались в Европе с конца пятнадцатого до конца девятнадцатого века. Общее горизонтальные солнечные часы это геометрический проекция из экваториальные солнечные часы на горизонтальную плоскость.

Особые свойства полярно указывающий гномон (осевой гномон) были впервые известны мавританскому астроному Абдул Хасан Али в начале тринадцатого века^[1] и это привело к уже знакомым нам циферблатным пластинам, на которых стиль и часовые линии имеют общий корень.

На протяжении веков ремесленники использовали различные методы для разметки часовых линий солнечных часов, используя методы, которые были им знакомы, кроме того, эта тема увлекла математиков и стала предметом изучения. Когда-то обычно преподавали графическую проекцию, но ее заменили тригонометрия, логарифмы, слайд-правила и компьютеры который сделал арифметические расчеты становится все более тривиальным. Графическая проекция когда-то была основным методом размещения солнечных часов, но отошла на второй план и теперь представляет только академический интерес.

Первый известный документ на английском языке, описывающий схему для графической проекции, был опубликован в Шотландии в 1440 году, что привело к серии отдельных схем для горизонтальных циферблатов, каждый с характеристиками, подходящими для цели. широта и способ строительства того времени.

Контекст

Мечеть Омейядов, также известная как Большая мечеть Дамаска.

Искусство дизайна солнечных часов заключается в создании циферблата, точно отображающего местное время. Дизайнеры солнечных часов также были очарованы математикой циферблата и возможными новыми способами отображения информации. Современный набор номера начался в десятом веке, когда арабские астрономы сделали великое открытие: гномон, параллельный оси Земли, будет производить солнечные часы, чьи часовые линии показывают равные часы или же юридические часы в любой день года: циферблат Ибн аль-Шатир в Мечеть Омейядов в Дамаск является самым старым циферблатом этого типа. ^[а] Циферблаты этого типа появились в Австрии и Германии в 1440-х годах.^[2]

Циферблат может быть выложен прагматичным подходом, наблюдая и отмечая тень через равные промежутки времени в течение дня в каждый день года. Если широта как известно, циферблат можно разложить с помощью геометрические методы построения которые полагаются на геометрия проекции, либо расчетом по известным формулам и тригонометрические таблицы обычно используя логарифмы, или же правила слайдов или совсем недавно компьютеры или же мобильные телефоны. Линейная алгебра предоставил полезный язык для описания трансформации.

В схеме солнечных часов используется компас и линейка чтобы сначала получить основные углы для этой широты, а затем использовать их для рисования часовых линий на циферблате. В современной терминологии это означало бы, что для получения ${ Displaystyle грех х}$ и ${ Displaystyle м загар у}$ и от этого ${ Displaystyle грех х. загар у}$. ^[b]

Базовый расчет

• Используя большой лист бумаги.
• Начиная снизу проводится горизонтальная линия, а вверх по центру - вертикальная. Там, где они пересекаются, становится начало О, подножие Гномона.
• Горизонтальной линией проведите линию, фиксирующую размер циферблата. Там, где он пересекает центральную линию, является важная точка построения F.
• Строительная линия проводится вверх от точки O под углом широты.^[c]
• Используя квадрат (опустите линию), проведите линию от F до вспомогательной линии так, чтобы они пересекались под прямым углом. Эта точка E - важная точка построения. Если быть точным, важна именно линия FE, так как она длина. ${ Displaystyle грех фи}$.
• Используя циркуль или делители, длина FE была скопирована вверх по центральной линии от F. Новая точка построения называется G. Линии построения и FE стираются.

• 

  Выставляем шкалу на 52 ° с. Три начальных строки.

• 

  Разметка широты, разметка длины ${ Displaystyle грех фи}$, и копирование в G по вертикали.

• 

  Тангенс: определение длины ${ displaystyle tan theta}$

• 

  Касательная к синусу: нанесение отрезков длины ${ displaystyle sin phi tan h}$, где h - целое число 0 .. 5

Такие геометрические конструкции были хорошо известны и оставались частью учебной программы средней школы (британской гимназии) до Новая математика революция 1970-х.^[3]

Схема, показанная выше, использовалась в 1525 г. (из более ранней работы 1440 г.) Дюрер все еще используется сегодня. Более простая схема больше подходила для циферблатов, предназначенных для более низких широт, требующих узкого листа бумаги для изготовления, чем для циферблатов, предназначенных для более высоких широт. Это побудило к поиску других построек.

Горизонтальные циферблаты

Первая часть процесса является общей для многих методов. Он устанавливает точку на линии север-юг, которая находится на расстоянии sin φ от линии меридиана.

Ранний шотландский метод (1440 г.) Дюрер (1525 г.) Рор (1965 г.)

• Начните с основного метода, показанного выше
• От G проведена серия линий, разнесенных на 15 °, достаточно длинных, чтобы пересекать линию, проходящую через F. Они отмечают часовые точки 1, 2, 3, 4, 5 и 7, 8, 9, 10, 11.
• Центр циферблата находится внизу, точка O. Линия, проведенная от каждой из этих часовых точек до точки O, будет часовой линией на готовом циферблате.^[4]

Существенная проблема - это ширина бумаги, необходимая в более высоких широтах. ^[5]

• 

  Выставляем шкалу на 52 ° с. Три начальных строки.

• 

  Разметка широты, разметка длины ${ Displaystyle грех фи}$, и копирование в G по вертикали.

• 
• 
• 

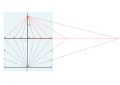
Бенедетти (1574)

Бенедетти, бедный дворянин, работал математиком при дворе Саволы. Его книга, описывающая этот метод, была De gnomonum umbrarumque солярий usu опубликовано в 1574 году. В нем описывается метод отображения юридических часов, то есть равных часов, которые мы используем сегодня, в то время как большинство людей по-прежнему использовали неравные часы, которые делили дневное время на 12 равных часов, но они будут меняться с течением года. Метод Бенедеттиса делит квадрант на сегменты по 15 °. Сделаны две конструкции: параллельная горизонтальная линия, определяющая расстояния tan h, и гномоническая полярная линия GT, которая представляет sin φ.

• Нарисуйте квадрант GRB с сегментами 15 °. GR - горизонтальный.
• Параллельная горизонтальная линия проведена из полиэтилена и сделаны отметки там, где она делит пополам лучи под углом 15 °.
• GX - это широта. T - точка пересечения с PE. ГТД - это гномонический треугольник.
• Длина GT копируется в нижнюю часть E, получая точку F.
• Часовые линии нарисованы от буквы F, и циферблат готов.

Бенедетти включил инструкции по рисованию точечного гномона, чтобы можно было нанести на график неравные часы.^[6]

• 

  Квадрант с сегментами 15 °.

• 

  построение лучей.

• 

  В поисках происхождения.

• 

  Добавление часовых линий.

• 

  Циферблат циферблата.

Метод Клавия (1586)

(Fabica et usus Instrumenti ad horologiorum descriptionem.) Рим, Италия.

Метод Клавиуса смотрит на четверть циферблата. Горизонтальная и перпендикулярная плоскости к полярной оси отображаются в виде двух прямоугольников, шарнирно соединенных с верхним краем обоих циферблатов. полярная ось будет на φ градусов к полярной оси, а часовые линии будут равномерно распределены в полярной плоскости на экваториальном циферблате. (15 °). Часовые точки на полярной плоскости соединятся с совпадающей точкой на горизонтальной плоскости. Горизонтальные часовые линии откладываются до начала координат.

^[7]

• Нарисуйте гномический треугольник, лежащий на нем гипотенузу.
• На маленькой стороне нарисуйте (экваториальный) квадрат с разметкой 15 ° часов.
• Циферблат состоит из циркуля, размеры которого взяты из треугольника.
• Часовые линии 12, 3 и 6 известны. Часовые линии 1 и 2 взяты со стороны квадрата.
• Диагональ берется от 12 до 6, и параллельные ей прямые проходят через 1 и 2, давая 5 и 4.
• Утренний циферблат - отражение этого.

Метод Стиррапа (1652 г.)

• От G проведена серия линий под углом 15 °, достаточно длинных, чтобы пересекать линию, проходящую через F. Они отмечают часовые точки 9, 10, 11, 12, 1, 2, 3.
• Центр циферблата находится внизу, точка O. Линия, проведенная от каждой из этих часовых точек до точки O, будет часовой линией на готовом циферблате.

^[5]

• 

  Выставляем шкалу на 52 ° с. Три начальных строки.

• 

  Разметка широты, разметка длины ${ Displaystyle грех фи}$, и копирование в G по вертикали.

• 

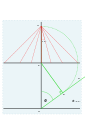
  С кастинга G ${ Displaystyle загар ч грех фи}$ по горизонтали.

• 

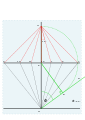
  Фактические часовые строки 9, 10, 11, 12, 1, 2, 3.

• 

  Строительные линии удалены.

• 

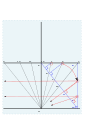
  Нахождение угла для 4 и 5.

• 

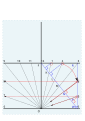
  Рисунок 4 и 5.

• 

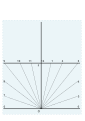
  Строительные линии удалены. Готовая циферблат на 52 ° с. Стремена (1652)

Метод Беттини (1660 г.)

В Иезуит Марио Беттини придумал метод, который был посмертно опубликован в книге Recreationum Mathematicarum Apiaria Novissima 1660.

• Нарисуйте гномонический треугольник с гипотенузой против меридиан линия, а φ - вниз, C. Другая точка называется M, а прямой угол - G.
• Через M проводится горизонтальная линия, это равноденственный
• Нарисована окружность с центром в M и радиусом MG. G2 и G3 - это точки пересечения окружности и меридиана.
• В верхних квадрантах точки отмечены каждые 30 °. Двое названы P, Q.
• Строительные линии проводятся от G2 и G3 через точки P и Q - точки пересечения с равноденствием отмечены.
• В завершение через эти точки от точки C проводят часовые линии, а циферблат вырезают в квадрат.

^[8]

• Метод Беттини 1660
• 

  Гномонический треугольник

• 

  Круг отмечен каждые 30 °

• 

  Строительные линии

• 

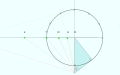
  Часовые линии, проведенные к началу координат

• 

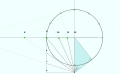
  Циферблат

Лейборн (1669)

Уильям Лейборн опубликовал его "Искусство набора номера"^[d] в 1669 г. с ним применяется шестиступенчатый метод. Его описание во многом опирается на термин линия аккордов, для которого современный список набора заменяет транспортир. Линия аккордов была шкалой, найденной на сектор который использовался вместе с набором разделителей или циркуля. Он использовался мореплавателями до конца 19 века.^[e]

• Нарисуйте круг и два его основных диаметра: E – W и S – N (сверху вниз). O - их точка пересечения или происхождение.
• Используя гамма аккордов или транспортир, отложите две строчки, «0а» то есть 52 ° от ОС, и "0b" то есть 52 ° от OW. (они будут под прямым углом. Точки «а» и «б» важны.
• Прямым краем нарисуйте линию, соединяющую E с «a», она пересекает SN (меридиональная линия) в точке P, которая называется полюс мира. Теперь подключите E к «a», это соединит AE. Этот момент важен, поскольку именно здесь меридиан пересекает равноденственный круг. Точки E, AE и W лежат на равноденственном круге. Следующая задача - использовать эту информацию, чтобы найти центр и нарисовать круг. Используйте вспомогательную линию, чтобы соединить AE и W. В центральной точке поднимите линию под прямым углом. Место пересечения SN (меридиана) будет C, центром равноденственного круга. Используйте C, чтобы нарисовать дугу от E до W, она пройдет через AE.
• Теперь есть полукруг, проходящий через E и W, и дуга равноденствия, проходящая через E и W. Разделите полукруг на 12 равных частей, то есть на углы 15 °. Отметьте «точкой построения». ^[f]
• Линейка соединяет точку O с точками полукруга. Эти линии пересекают дугу равноденствия: создается серия неравных точек («маркеров»).
• Линейка от P (полюса мира) проводит линию от этих маркеров обратно через полукруг. Где он сокращается, это будет «часовая точка»; эти часовые точки расположены неравномерно.
• Часовые линии проводятся от каждой из этих «часовых точек» до начала координат. Исток - основа стиля, срезанного под углом 52 °. ^[10][5]

Метод Озанама (1673 г.) Майол (1938 г.)

Для этого метода требуется лист бумаги гораздо меньшего размера,^[5] большое преимущество для более высоких широт.

• От G проводится серия линий, разнесенных на 15 °, достаточно длинных, чтобы они пересекали линию, проходящую через F. Они отмечают часовые точки 9, 10, 11, 12, 1, 2, 3 и представляют собой точки. ${ Displaystyle загар ч грех фи}$.
• Центр циферблата находится внизу, точка O. Линия, проведенная от каждой из этих часовых точек до точки O, будет часовой линией на готовом циферблате.^[4]
• Линии через 9 и 3 продолжаются до линии WE, а линия, перпендикулярная от 9 и 3 к линии WE, называются точками пересечения W 'и E'. От W и E еще две линии проведены на расстоянии 15 ° друг от друга, они пересекают вертикали, образуя часовые точки 7, 8 и 4, 5. Линии от 0 до этих часовых точек являются часовыми линиями на последнем циферблате.

^[5]

• 

  Выставляем шкалу на 52 ° с. Три начальных строки.

• 

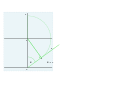
  Разметка широты, разметка длины ${ Displaystyle грех фи}$, и копирование в G по вертикали.

• 

  С кастинга G ${ Displaystyle загар ч грех фи}$ по горизонтали.

• 

  Фактические часовые строки 9, 10, 11, 12, 1, 2, 3.

• 

  Строительные линии удалены.

Энциклопедический метод (1771 г.)

Этот метод использует свойства хорд для определения расстояния ${ Displaystyle м. грех тета}$ в верхнем квадранте, а затем переносит это расстояние в нижний квадрант, так что ${ Displaystyle грех фи грех тета}$ Установлено. Опять перенос этой меры на хорды в верхнем квадранте. Последние строки устанавливают формулу ${ Displaystyle загар каппа =}$ ${ Displaystyle грех тета грех фи над соз тета}$ = ${ Displaystyle загар тета грех фи}$

Затем он симметрично переносится на все квадранты. Он использовался в Британская энциклопедия Первое издание 1771 г., шестое издание 1823 г.^[11]

• Гномон рисуется первым по линии север-юг. При этом диаметр при φ градусы к вертикали нарисованы; его отражение тоже будет необходимо.
• Окружность размечена с интервалом 15 ° в верхних квадрантах. Рисуются хорды, параллельные горизонтали (длина этих хорд будет sin.
• Измерение каждой хорды переносится на шкалу по нижним радиусам. При соединении эти точки образуют серию параллельных линий, равных sin θ. sin φ по длине.
• Эти измерения переносятся на хорду.
• Последние часовые линии проводятся от исходных точек через эти точки пересечения. ( ${ Displaystyle загар каппа =}$ ${ Displaystyle грех тета грех фи над соз тета}$ = ${ Displaystyle загар тета грех фи}$ )^[12]

• 

  Нарисуйте гномон и диаметры под заданным углом.

• 

  Отметьте верхние квадранты под углом 15 ° и соедините хордами.

• 

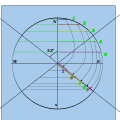
  Перенесите длину полухорды на нижний радиус и проведите поперек.

• 

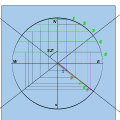
  Поднимите вертикали

• 

  Проведите часовую линию через пересечения.

• 

  Полученный циферблат на 52 °.

де Целль (1760) (1790) Метод Во (1973)

В Dom Francois Bedos de Celles метод (1760) ^[13] иначе известный как метод Во (1973) ^[14][5]

• От G проведена серия линий под углом 15 °, достаточно длинных, чтобы они пересекали линию, проходящую через F. Они отмечают часовые точки 9, 10, 11, 12, 1, 2, 3, если вы возьмете всего 3 и представите точки. ${ Displaystyle загар ч грех фи}$.
• Центр циферблата находится внизу, точка O. Линия, проведенная от каждой из этих часовых точек до точки O, будет часовой линией на готовом циферблате.^[4]
• Если бумага достаточно велика, описанный выше метод работает от 7 до 12 и от 12 до 5, а значения до и после 6 рассчитываются посредством симметрии. Однако есть другой способ разметки 7 и 8, 4 и 5. Назовите точку, где 3 пересекает линию R, и проведите линию под прямым углом к ​​базовой линии. Назовите эту точку W. Используйте строительную линию, чтобы соединить точки W и F. Во назовите точки пересечения линиями часов K, L, M.
• Используя циркуль или делитель, добавьте еще две точки к этой линии N и P, чтобы расстояния MN = ML, а MP = MK. Отсутствующие часовые линии проводятся от O до N и через P. Линии построения стираются.^{[4] [5]}

• 

  Выставляем шкалу на 52 ° с. Три начальных строки.

• 

  Разметка широты, разметка длины ${ Displaystyle грех фи}$, и копирование в G по вертикали.

• 

  С кастинга G ${ Displaystyle загар ч грех фи}$ по горизонтали.

• 

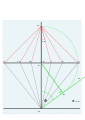
  Фактические часовые строки 9, 10, 11, 12, 1, 2, 3.

• 

  Строительные линии удалены.

• 

  Построение 7, 8, 4, 5 линий

• 

  Разметка 7, 8, 4, 5 строк

• 

  Готовая циферблат на 52 ° с. Бедос де Селлес (1790)

Метод Николсона (1825 г.)

Этот метод впервые появился у Питера Николсона. Популярный курс чистой и смешанной математики в 1825 году. Его скопировали в School World в июне 1903 года, затем в «Солнечные часы и сферы» Кеннета Линча в 1971 году. ^[15] Он начинается с рисования хорошо известного треугольника и берет вершины, чтобы нарисовать две окружности с радиусами (OB) sin φ и (AB) tan φ. Проведены линии 15 °, пересекающие эти круги. Линии берутся по горизонтали, а по вертикали от этих кругов и точка их пересечения (OB sin t, AB cos t) находится на часовой линии. То есть tan κ = OB sin t / AB cos t, что сводится к sin φ. загар т.

• Нарисуйте линию NS и линию EW, пересекающуюся в начале O. В удобной точке в первом квадранте соедините оси линией, установленной под целевым углом. Это образует основной треугольник OAB.
• Установите циркуль на расстояние ОВ и начертите круг. Установите циркуль на AB и начертите концентрический круг. На обоих этих кругах отметьте углы 15 °.
• Беря линии вертикально от внутреннего круга и горизонтально от внешнего круга, отметьте каждое из пересечений. Это на часовых линиях.
• Соедините точки пересечения с началом координат.

^[15]

• 

  Основной треугольник

• 

  Круги

• 

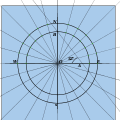
  Измерение 15 °

• 

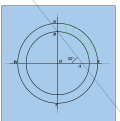
  Точки пересечения

• 

  Готовый циферблат

Весы для набора номера Foster Serles (1638)

• На циферблате нанесен прямой угол, а шкала широты нанесена на циферблат. Икс-ось.
• Точка целевой широты отмечена на циферблате. Часовая шкала располагается от этой точки до полуденной линии (условно, нулевая точка находится на полуденной линии).
• Каждая из часовых точек копируется на циферблат, и эта процедура повторяется, давая часам обе стороны полудня. Прямая кромка используется для соединения этих точек с началом координат, таким образом рисуя часовые линии для этого местоположения.
• Вертикальная линия от точки целевой широты и горизонтальная линия, проходящая через точку полудня, будут делиться пополам на отметке трех часов (9: 00–15: 00).
• Стиль будет под тем же углом, что и широта.

^[16]

Сафея (Ас-Сафия)

Это был ранний и удобный метод использования, если у вас был доступ к астролябия так много астрологи и математики того времени было бы. Метод заключался в копировании проекций небесная сфера на плоскую поверхность. Проведена вертикальная линия с линией под углом к ​​широте, проведенной на пополам вертикали с небесной сферой. ^[17]

Смотрите также

• Лондонский циферблат
• Схема для вертикально убывающих циферблатов

Примечания

Рекомендации

Цитаты

Источники

• Дурелл, Клемент V (1921). Геометрия. Издатель G.Bell And Sons Limited.CS1 maint: ref = harv (связь)
• Бедос де Селлес, Франсуа (1760). "4-3". La Gnomonique pratique ou l'Art de tracer les cadrans solaires avec la plus grande précision (на французском языке) (3-е изд.). Париж. п. 459. Получено 12 июля 2015.CS1 maint: ref = harv (связь)
• Дэвис, Джон (июнь 2014 г.). «Гравированный декор английских горизонтальных циферблатов» (PDF). Бюллетень. Британское общество солнечных часов. 26 (ii): 48–52. ISSN  0958-4315. Получено 3 июля 2015.CS1 maint: ref = harv (связь)
• Рор, Рене Р.Дж. ; с предисловием Анри Мишеля; перевод Габриэля Година (1996). Солнечные часы: история, теория и практика (Мягкая обложка ред.). Нью-Йорк: Dover Publications. стр.142. ISBN  0-486-29139-1.CS1 maint: ref = harv (связь)
• Сойер, Фред (1995). "Наборные весы Серле". Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 2 (2): 5.
• Сойер, Фред (2012). «Горизонтальные схемы 1–4». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 19 (1): 33.
• Сойер, Фред (2012). «Горизонтальные схемы 6». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 19 (3): 36–7.
• Сойер, Фред (2012). «Горизонтальные схемы 7». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 19 (4): 39.
• Гунелла, Алессандро (2013). Сойер, Фред (ред.). «Горизонтальные схемы 8 - Метод Клавиуса». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 20 (1): 31.CS1 maint: ref = harv (связь)
• Гунелла, Алессандро (2013). Сойер, Фред (ред.). «Горизонтальные схемы 9 - Метод Бенедетти». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 20 (2): 37.
• Гунелла, Алессандро (2013). Сойер, Фред (ред.). «Горизонтальные схемы 10 - Метод Сафеи». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 20 (3): 39.
• Гунелла, Алессандро (2013). Сойер, Фред (ред.). «Горизонтальные схемы 11 - все еще метод для горизонтальных солнечных часов». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 21 (3): 13.
• Пауэрс, Патрик (2012). Сойер, Фред (ред.). «Горизонтальные схемы 5 - Метод Лейборна». Компендиум. Гластонбери, Коннектикут, США: Североамериканское общество солнечных часов. 19 (2): 4.
• Во, Альберт Э. (1973). Солнечные часы: их теория и конструкция. Нью-Йорк: Дувр. стр.38–39. ISBN  0486229475.CS1 maint: ref = harv (связь)