Пара туси - Tusi couple

Анимированная модель пары Туси.

В Пара туси это математический устройство, в котором небольшой круг вращается внутри большего круга вдвое больше диаметр меньшего круга. Вращение кругов приводит к появлению точки на длина окружности меньшего круга в колебаться вперед и назад в линейное движение по диаметру большего круга. Пара Туси - это двуплечий гипоциклоида.

Пара была впервые предложена в 13 веке. Персидский астроном и математик Насир ад-Дин ат-Туси в его 1247 Тахрир аль-Маджисти (Комментарий к Альмагесту) как решение для широтного движения нижних планет,[1] и позже широко использовался как замена равный введен более тысячи лет назад в Птолемей с Альмагест.[2][3]

Исходное описание

Диаграмма Туси пары Туси, 13 век[4]

Туси описал кривую следующим образом:

Если две копланарные окружности, диаметр одной из которых равен половине диаметра другой, считаются касательными внутри в точке, и если точка берется на меньшей окружности - и пусть она находится в точке касание - и если два круга движутся простыми движениями в противоположном направлении таким образом, что движение меньшего [круга] вдвое больше, чем движение большего, поэтому меньший совершает два поворота для каждого поворота большего, тогда эта точка будет видно, как он движется по диаметру большего круга, который первоначально проходит через точку касания, колеблясь между конечными точками.[5]

Алгебраически это может быть выражено комплексными числами как

Другие комментаторы заметили, что пару Туси можно интерпретировать как кривая качения где вращение внутреннего круга удовлетворяет условию отсутствия проскальзывания, поскольку его касательная точка движется вдоль фиксированного внешнего круга.

Связь с астрономическими теориями ат-Туси

Насир ад-Дин ат-Туси, родился в городе Тус, Иран в 1201 году признан во всем исламском мире одной из «великих мудростей». Туси был первым астрономом, который попытался найти решение, которое обеспечило бы широтное движение без введения продольной составляющей. Для этого он предложил в своей работе под названием «Тахрир аль-Маджисти», завершенной в 1247 году, что колебательное движение вызывается объединенными однородными круговыми движениями двух одинаковых кругов, одна из которых движется по окружности другой. В этот момент Туси просто заявляет, что если бы одна из этих окружностей двигалась с постоянной скоростью, вдвое превышающей скорость другой, и в направлении к ней, то любая точка на окружности первой окружности колебалась бы прямая по одному из диаметров второй окружности[6]

Другие источники

Термин «пара Туси» - современный термин, придуманный Эдвард Стюарт Кеннеди в 1966 г.[7] Это одно из нескольких позднеисламских астрономических устройств, поразительно похожих на модели в Николай Коперник с De Revolutionibus, включая его Меркурий модель и его теория трепет. Историки подозревают, что Коперник или другой европейский автор имел доступ к арабскому астрономическому тексту, но точная цепь передачи еще не установлена.[8] хотя ученый и путешественник 16 века Гийом Постель было предложено.[9][10]

Поскольку пара Туси использовалась Коперником в его переформулировке математической астрономии, растет согласие с тем, что он каким-то образом осознал эту идею. Это было предложено[11][12] что идея пары Туси, возможно, прибыла в Европу, оставив мало следов рукописей, так как это могло произойти без перевода какого-либо арабского текста на латынь. Один из возможных путей передачи мог быть через Византийская наука, которая перевела некоторые произведения ат-Туси с арабского на Византийский греческий. Несколько византийских греческих рукописей, содержащих пару Туси, все еще сохранились в Италии.[13]

Существуют и другие источники этой математической модели для преобразования круговых движений в возвратно-поступательное линейное движение. Он находится в Прокла Комментарий к первой книге Евклид[14] и эта концепция была известна в Париже к середине 14 века. В его вопросы на Сфера (написано до 1362 г.), Николь Орем описал, как комбинировать круговые движения, чтобы произвести возвратно-поступательное линейное движение планеты по радиусу ее эпицикла. Описание Орема неясно, и неясно, представляет ли это самостоятельное изобретение или попытку разобраться с плохо понимаемым арабским текстом.[15]

Более поздние примеры

Хотя пара Туси была разработана в астрономическом контексте, более поздние математики и инженеры разработали аналогичные версии того, что стало называться гипоциклоида прямолинейные механизмы. Математик Джероламо Кардано разработал систему, известную как Карданный механизм (также известный как Карданная передача).[16] Инженеры девятнадцатого века Джеймс Уайт,[17] Мэтью Мюррей,[18] а также более поздние конструкторы разработали практические приложения гипоциклоидного прямолинейного механизма.

Гипотрохоид

Основная статья: Гипотрохоид
В эллипсы (зеленый, голубой, красный) являются гипотрохоиды пары Туси.

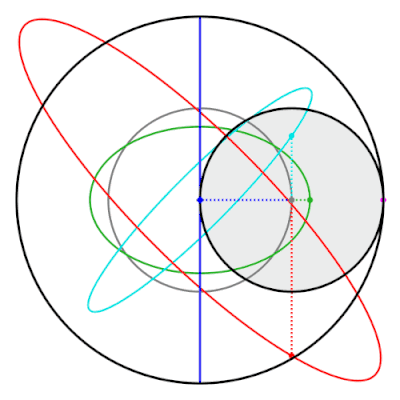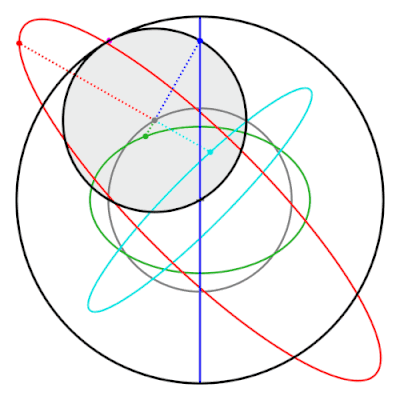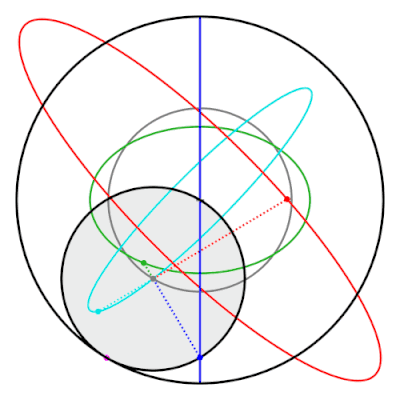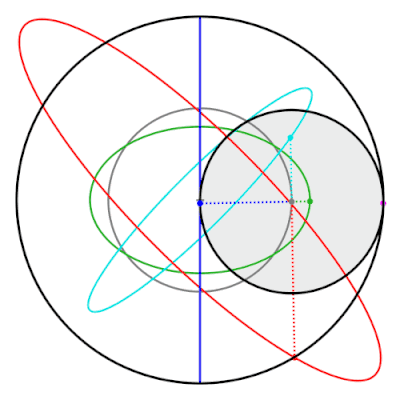
Свойство пары Туси состоит в том, что точки на внутреннем круге, которые не находятся на следе окружности эллипсы. Эти эллипсы и прямая линия, проведенная классической парой Туси, являются частными случаями гипотрохоиды.[19]

Смотрите также

Примечания

  1. ^ Джордж Салиба (1995), 'История арабской астрономии: планетарные теории в золотой век ислама ', стр.152-155
  2. ^ «Позднесредневековая планетная теория», Э. С. Кеннеди, Исида 57, # 3 (осень 1966 г.), 365-378, JSTOR  228366.
  3. ^ Крейг Г. Фрейзер,Космос: историческая перспектива ', Greenwood Publishing Group, 2006 г., стр. 39
  4. ^ Библиотека Ватикана, НДС. ар. 319 л. 28 обратная математика19 NS.15 В архиве 2014-12-24 на Wayback Machine, копия рукописи из Туси, XIV в.
  5. ^ В переводе Ф. Дж. Рагепа, Воспоминания по астрономии II.11 [2], стр. 194, 196.
  6. ^ Салиба, Джордж; Кеннеди, Э.С. Арабские науки и философия (1-е изд.). С. 285–291.
  7. ^ Э. С. Кеннеди, "Планетарная теория позднего средневековья", с. 370.
  8. ^ Э. С. Кеннеди, "Планетарная теория позднего средневековья", с. 377.
  9. ^ Салиба, Джордж (1996), "Написание истории арабской астрономии: проблемы и разные точки зрения", Журнал Американского восточного общества, 116 (4): 709–18, Дои:10.2307/605441, JSTOR  605441, стр. 716-17.
  10. ^ Чья наука является арабской наукой в ​​Европе эпохи Возрождения? к Джордж Салиба, Колумбийский университет
  11. ^ Клаудия Крен, "Катящееся устройство", стр. 497.
  12. ^ Джордж Салиба, "Чья наука арабская наука в Европе эпохи Возрождения?" [1]
  13. ^ Джордж Салиба (27 апреля 2006 г.). "Исламская наука и становление Европы эпохи Возрождения". Получено 2008-03-01.
  14. ^ Веселовский, И. Н. (1973). «Коперник и Насир ад-Дин ат-Туси». Журнал истории астрономии. 4: 128–30. Bibcode:1973JHA ..... 4..128V. Дои:10.1177/002182867300400205. S2CID  118453340.
  15. ^ Клаудиа Крен, "Катящееся устройство", стр. 490-2.
  16. ^ Веселовский, И. Н. (1973). «Коперник и Насир ад-Дин ат-Туси». Журнал истории астрономии. 4: 128. Bibcode:1973JHA ..... 4..128V. Дои:10.1177/002182867300400205. S2CID  118453340.
  17. ^ "Словарь Аплтона машин, механики, машиностроения и инженерии". 1857.
  18. ^ "Polly Model Engineering: Комплекты стационарных двигателей - модели Энтони Маунта".
  19. ^ Бранде, W.T. (1875), Словарь науки, литературы и искусства, Лонгманс, Грин и Компания, стр. 181, получено 2017-04-10

Рекомендации

  • Ди Боно, Марио (1995). «Устройство Коперника, Амико, Фракасторо и Туси: наблюдения за использованием и передачей модели». Журнал истории астрономии. 26: 133–154. Bibcode:1995JHA .... 26..133D. Дои:10.1177/002182869502600203. S2CID  118330488.
  • Кеннеди, Э. С. (1966). «Позднесредневековая планетная теория». Исида. 57 (3): 365–378. Дои:10.1086/350144.
  • Крен, Клаудия (1971). "Катящееся устройство Накира ад-Дина аль-Хуси в De spera Николь Орем ". Исида. 62 (4): 490–498. Дои:10.1086/350791.
  • Рагеп, Ф. Дж. «Две версии пары Туси», в From Deferent to Equant: Сборник исследований по истории науки древнего и средневекового Ближнего Востока в честь Э. С. Кеннеди, изд. Дэвид Кинг и Джордж Салиба, Annals of the New York Academy of Sciences, 500. New York Academy of Sciences, 1987. ISBN  0-89766-396-9 (pbk.)
  • Рагеп, Ф. Дж. «Воспоминания по астрономии» Насира ад-Дина ат-Туси, Источники по истории математики и физических наук, 12. 2 тт. Берлин / Нью-Йорк: Springer, 1993. ISBN  3-540-94051-0 / ISBN  0-387-94051-0.

внешняя ссылка