Разрешающая способность - Permittivity

Диэлектрическая среда, показывающая ориентацию заряженных частиц, создающих эффекты поляризации. Такая среда может иметь более низкое отношение электрического потока к заряду (большую диэлектрическую проницаемость), чем пустое пространство.

Статьи о
Электромагнетизм
Электричество Магнетизм История Учебники
Электростатика Электрический заряд Закон Кулона Дирижер Плотность заряда Разрешающая способность Электрический дипольный момент Электрическое поле Электрический потенциал Электрический поток  / потенциальная энергия Электростатический разряд Закон Гаусса Индукция Изолятор Плотность поляризации Статичное электричество Трибоэлектричество
Магнитостатика Закон Ампера Закон Био – Савара Закон Гаусса для магнетизма Магнитное поле Магнитный поток Магнитный дипольный момент Магнитная проницаемость Магнитный скалярный потенциал Намагничивание Магнитодвижущая сила Правило правой руки
Электродинамика Закон силы Лоренца Электромагнитная индукция Закон Фарадея Закон Ленца Ток смещения Магнитный векторный потенциал Уравнения Максвелла Электромагнитное поле Электромагнитный импульс Электромагнитное излучение Тензор Максвелла Вектор Пойнтинга Потенциал Льенара – Вихерта Уравнения Ефименко Вихревой ток Уравнения Лондона Математические описания электромагнитного поля
Электрическая сеть Переменный ток Емкость Постоянный ток Электрический ток Электролиз Плотность тока Джоулевое нагревание Электродвижущая сила Импеданс Индуктивность Закон Ома Параллельная схема Сопротивление Резонансные полости Последовательная схема Напряжение Волноводы
Ковариантная формулировка Электромагнитный тензор (тензор энергии-импульса ) Четырехтоковый Электромагнитный четырехпотенциальный
Ученые Ампер Биот Кулон Дэви Эйнштейн Фарадей Физо Гаусс Хевисайд Генри Герц Джоуль Ленц Лоренц Максвелл Ørsted Ом Ричи Savart Певица Тесла Вольта Вебер

В электромагнетизм, то абсолютная диэлектрическая проницаемость, часто просто называют диэлектрическая проницаемость и обозначается Греческая буква ε (эпсилон), это мера электрического поляризуемость из диэлектрик. Материал с высокой диэлектрической проницаемостью поляризуется больше в ответ на приложенное электрическое поле, чем материал с низкой диэлектрической проницаемостью, тем самым накапливая больше энергии в материале. В электростатика, диэлектрическая проницаемость играет важную роль в определении емкость конденсатора.

В простейшем случае электрическое поле смещения D в результате применения электрическое поле E является

${ displaystyle mathbf {D} = varepsilon mathbf {E}.}$

В более общем смысле диэлектрическая проницаемость - это термодинамический функция государства ^[1]. Это может зависеть от частота, величина, и направление прикладного поля. В SI единица диэлектрической проницаемости фарад на метр (Ф / м).

Диэлектрическая проницаемость часто представлена относительная диэлектрическая проницаемость ε_р что является отношением абсолютной диэлектрической проницаемости ε и диэлектрическая проницаемость вакуума ε₀

${ displaystyle kappa = varepsilon _ { mathrm {r}} = { frac { varepsilon} { varepsilon _ {0}}}}$.

Эту безразмерную величину также часто и неоднозначно называют диэлектрическая проницаемость. Другой общий термин, встречающийся как для абсолютной, так и для относительной диэлектрической проницаемости, - это диэлектрическая постоянная который устарел в физике и инженерии^[2] а также в химии.^[3]

По определению, идеальный вакуум имеет относительную диэлектрическую проницаемость ровно 1, тогда как при STP, воздух имеет относительную диэлектрическую проницаемость κ_{воздуха} = 1.0006.

Относительная диэлектрическая проницаемость напрямую связана с электрическая восприимчивость (χ) от

${ Displaystyle чи = каппа -1}$

иначе записывается как

${ displaystyle varepsilon = varepsilon _ { mathrm {r}} varepsilon _ {0} = (1+ chi) varepsilon _ {0}}$

Единицы

Стандартная единица измерения диэлектрической проницаемости в системе СИ - фарад на метр (Ф / м или Ф · м.⁻¹).^[4]

${ displaystyle { frac { text {F}} { text {m}}} = { frac { text {C}} {{ text {V}} { cdot} { text {m} }}} = { frac {{ text {C}} ^ {2}} {{ text {N}} { cdot} { text {m}} ^ {2}}} = { frac { { text {C}} ^ {2} { cdot} { text {s}} ^ {2}} {{ text {kg}} { cdot} { text {m}} ^ {3} }}}$

Объяснение

В электромагнетизм, то электрическое поле смещения D представляет собой распределение электрических зарядов в данной среде в результате наличия электрического поля E. Это распределение включает миграцию заряда и электрическую диполь переориентация. Его связь с диэлектрической проницаемостью в очень простом случае линейный, однородный, изотропный материалы с «мгновенный» ответ к изменениям электрического поля относится:

${ Displaystyle mathbf {D} = varepsilon mathbf {E}}$

где диэлектрическая проницаемость ε это скаляр. Если среда анизотропный диэлектрическая проницаемость второго ранга тензор.

В общем, диэлектрическая проницаемость не является постоянной величиной, так как она может меняться в зависимости от положения в среде, частоты приложенного поля, влажности, температуры и других параметров. В нелинейная среда, диэлектрическая проницаемость может зависеть от напряженности электрического поля. Диэлектрическая проницаемость как функция частоты может принимать действительные или комплексные значения.

В единицах СИ диэлектрическая проницаемость измеряется в фарады на метр (Ф / м или А²· С⁴·кг⁻¹· М⁻³). Поле смещения D измеряется в единицах кулоны на квадратный метр (См²), а электрическое поле E измеряется в вольт на метр (В / м). D и E описывают взаимодействие между заряженными объектами. D относится к плотности заряда связанных с этим взаимодействием, а E относится к силы и потенциальные различия.

Диэлектрическая проницаемость вакуума

Диэлектрическая проницаемость вакуума ε₀ (также называется диэлектрическая проницаемость свободного пространства или электрическая постоянная) - отношение D/E в свободное место. Он также появляется в Постоянная кулоновской силы,

${ displaystyle k _ { text {e}} = { frac {1} {4 pi varepsilon _ {0}}}}$

Его ценность^[5]

${ displaystyle varepsilon _ {0} { stackrel { mathrm {def}} {=}} { frac {1} {c_ {0} ^ {2} mu _ {0}}} = { гидроразрыв {1} {35 , 950 , 207 , 149.472 , 7056 pi}} { text {F / m}} приблизительно 8.854 , 187 , 8176 ldots times 10 ^ {- 12} { text {F / m}}}$

где

• c₀ это скорость света в свободном пространстве,^[а]
• µ₀ это вакуумная проницаемость.

Константы c₀ и μ₀ были определены в единицах СИ, чтобы иметь точные числовые значения до переопределения единиц СИ в 2019 году.^[7] (Приближение во втором значении ε₀ выше проистекает из π будучи иррациональный номер.)

Относительная диэлектрическая проницаемость

Линейная диэлектрическая проницаемость однородного материала обычно дается относительно диэлектрической проницаемости свободного пространства как относительная диэлектрическая проницаемость ε_р (также называется диэлектрическая постоянная, хотя этот термин не рекомендуется и иногда относится только к статической относительной диэлектрической проницаемости при нулевой частоте). В анизотропном материале относительная диэлектрическая проницаемость может быть тензором, вызывая двулучепреломление. Фактическая диэлектрическая проницаемость затем рассчитывается путем умножения относительной диэлектрической проницаемости на ε₀:

${ displaystyle varepsilon = varepsilon _ { mathrm {r}} varepsilon _ {0} = (1+ chi) varepsilon _ {0},}$

где χ (часто пишется χ_е) - электрическая восприимчивость материала.

Восприимчивость определяется как константа пропорциональности (которая может быть тензор ) относящиеся к электрическое поле E к индуцированному диэлектрик плотность поляризации п такой, что

${ Displaystyle mathbf {P} = varepsilon _ {0} chi mathbf {E},}$

где ε₀ это электрическая проницаемость свободного пространства.

Восприимчивость среды связана с ее относительной диэлектрической проницаемостью. ε_р от

${ displaystyle chi = varepsilon _ { mathrm {r}} -1.}$

Итак, в случае вакуума

${ displaystyle chi = 0.}$

Восприимчивость также связана с поляризуемость отдельных частиц в среде Соотношение Клаузиуса-Моссотти.

В электрическое перемещение D связана с плотностью поляризации п от

${ displaystyle mathbf {D} = varepsilon _ {0} mathbf {E} + mathbf {P} = varepsilon _ {0} (1+ chi) mathbf {E} = varepsilon _ { mathrm {r}} varepsilon _ {0} mathbf {E}.}$

Диэлектрическая проницаемость ε и проницаемость µ среды вместе определяют фазовая скорость v = c/п из электромагнитное излучение через эту среду:

${ displaystyle varepsilon mu = { frac {1} {v ^ {2}}}.}$

Практическое применение

Определение емкости

Емкость конденсатора зависит от его конструкции и архитектуры, что означает, что она не изменяется при зарядке и разрядке. Формула для емкости в конденсатор с параллельными пластинами записывается как

${ Displaystyle C = varepsilon { frac {A} {d}}}$

где ${ displaystyle A}$ площадь одной пластины, ${ displaystyle d}$ расстояние между пластинами, а ${ displaystyle varepsilon}$ - диэлектрическая проницаемость среды между двумя пластинами. Для конденсатора с относительной диэлектрической проницаемостью ${ displaystyle kappa}$, можно сказать, что

${ displaystyle C = kappa varepsilon _ {0} { frac {A} {d}}}$

Закон Гаусса

Диэлектрическая проницаемость связана с электрическим потоком (и, соответственно, с электрическим полем) через Закон Гаусса. Закон Гаусса гласит, что для закрытого Гауссова поверхность, с

${ displaystyle Phi _ {E} = { frac {Q _ { text {enc}}} { varepsilon _ {0}}} = oint _ {s} mathbf {E} cdot mathrm {d } mathbf {A}}$

где ${ displaystyle Phi _ {E}}$ - чистый электрический поток, проходящий через поверхность, ${ displaystyle Q _ { text {enc}}}$ - заряд, заключенный в гауссовой поверхности, ${ displaystyle mathbf {E}}$ - вектор электрического поля в данной точке на поверхности, а ${ Displaystyle mathrm {d} mathbf {A}}$ - вектор дифференциальной площади на гауссовой поверхности.

Если гауссова поверхность равномерно охватывает изолированное симметричное расположение зарядов, формулу можно упростить до

${ displaystyle EA cos ( theta) = { frac {Q _ { text {enc}}} { varepsilon _ {0}}}}$

где ${ displaystyle theta}$ представляет собой угол между вектором электрического поля и вектором площади.

Если все силовые линии электрического поля пересекают поверхность под углом 90 °, формулу можно упростить до

${ displaystyle E = { frac {Q _ { text {enc}}} { varepsilon _ {0} A}}}$

Поскольку площадь поверхности сферы равна ${ displaystyle 4 pi r ^ {2}}$, электрическое поле на расстоянии ${ displaystyle r}$ вдали от однородного сферического заряда

${ displaystyle E = { frac {Q} { varepsilon _ {0} A}} = { frac {Q} { varepsilon _ {0} left (4 pi r ^ {2} right)} }}$

${ displaystyle E = { frac {Q} {4 pi varepsilon _ {0} r ^ {2}}} = { frac {kQ} {r ^ {2}}}}$

где ${ displaystyle k}$ является Постоянная Кулона (${ displaystyle sim 9.0 times 10 ^ {9} { text {m}} / { text {F}}}$). Эта формула применяется к электрическому полю, создаваемому точечным зарядом, вне проводящей сферы или оболочки, за пределами однородно заряженной изолирующей сферы или между пластинами сферического конденсатора.

Дисперсия и причинность

В общем, материал не может поляризоваться мгновенно в ответ на приложенное поле, поэтому более общая формулировка как функция времени такова:

${ displaystyle mathbf {P} (t) = varepsilon _ {0} int _ {- infty} ^ {t} chi left (t-t ' right) mathbf {E} left ( t ' right) , dt'.}$

То есть поляризация свертка электрического поля в предыдущие моменты времени с зависимой от времени восприимчивостью, определяемой χ(Δт). Верхний предел этого интеграла можно продолжить до бесконечности, если определить χ(Δт) = 0 для Δт < 0. Мгновенный ответ будет соответствовать Дельта-функция Дирака восприимчивость χ(Δт) = χδ(Δт).

Удобно брать преобразование Фурье относительно времени и запишите это соотношение как функцию частоты. Из-за теорема свертки, интеграл становится простым произведением,

${ displaystyle mathbf {P} ( omega) = varepsilon _ {0} chi ( omega) mathbf {E} ( omega).}$

Эта частотная зависимость восприимчивости приводит к частотной зависимости диэлектрической проницаемости. Форма восприимчивости по частоте характеризует разброс свойства материала.

Более того, тот факт, что поляризация может зависеть только от электрического поля в предыдущие моменты времени (т.е. χ(Δт) = 0 для Δт < 0), как следствие причинность, навязывает Ограничения Крамерса – Кронига на восприимчивость χ(0).

Комплексная диэлектрическая проницаемость

Спектр диэлектрической проницаемости в широком диапазоне частот. ε′ и ε″ обозначают действительную и мнимую части диэлектрической проницаемости соответственно. На изображении обозначены различные процессы: ионная и диполярная релаксация, а также атомные и электронные резонансы при более высоких энергиях.^[8]

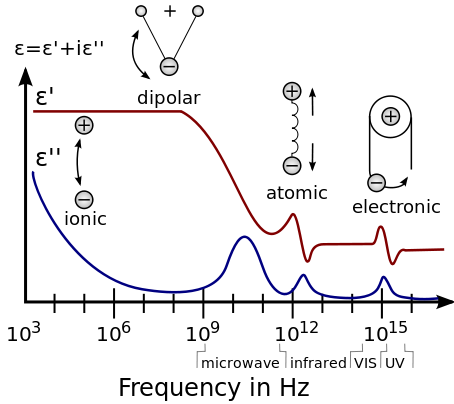
В отличие от реакции вакуума, реакция обычных материалов на внешние поля обычно зависит от частота поля. Эта частотная зависимость отражает тот факт, что поляризация материала не изменяется мгновенно при приложении электрического поля. Ответ всегда должен быть причинный (возникающий после приложенного поля), который может быть представлен разностью фаз. По этой причине диэлектрическую проницаемость часто рассматривают как сложную функцию (угловая частота ω прикладной области:

${ Displaystyle varepsilon rightarrow { hat { varepsilon}} ( omega)}$

(поскольку комплексные числа позволяют указывать величину и фазу). Таким образом, определение диэлектрической проницаемости становится

${ displaystyle D_ {0} e ^ {- i omega t} = { hat { varepsilon}} ( omega) E_ {0} e ^ {- i omega t},}$

где

• D₀ и E₀ - амплитуды смещения и электрического поля соответственно,
• я это мнимая единица, я² = −1.

Реакция среды на статические электрические поля описывается низкочастотным пределом диэлектрической проницаемости, также называемым статической диэлектрической проницаемостью. ε_s (также ε_{ОКРУГ КОЛУМБИЯ}):

${ displaystyle varepsilon _ { mathrm {s}} = lim _ { omega rightarrow 0} { hat { varepsilon}} ( omega).}$

На высокочастотном пределе (имеется в виду оптические частоты) комплексную диэлектрическую проницаемость обычно называют ε_∞ (или иногда ε_{выбрать}^[9]). На плазменная частота и ниже диэлектрики ведут себя как идеальные металлы с поведением электронного газа. Статическая диэлектрическая проницаемость является хорошим приближением для переменных полей низких частот, и по мере увеличения частоты измеряемая разность фаз δ возникает между D и E. Частота, при которой фазовый сдвиг становится заметным, зависит от температуры и характеристик среды. Для умеренной напряженности поля (E₀), D и E остаются пропорциональными, и

${ displaystyle { hat { varepsilon}} = { frac {D_ {0}} {E_ {0}}} = | varepsilon | e ^ {- i delta}.}$

Поскольку реакция материалов на переменные поля характеризуется комплексной диэлектрической проницаемостью, естественно разделить ее действительную и мнимую части, что по соглашению выполняется следующим образом:

${ Displaystyle { шляпа { varepsilon}} ( omega) = varepsilon '( omega) -i varepsilon' '' ( omega) = left | { frac {D_ {0}} {E_ {0 }}} right | left ( cos delta -i sin delta right).}$

где

• ε′ - действительная часть диэлектрической проницаемости;
• ε″ - мнимая часть диэлектрической проницаемости;
• δ это угол потерь.

Выбор знака зависимости от времени, е^−iωt, диктует соглашение о знаках для мнимой части диэлектрической проницаемости. Используемые здесь знаки соответствуют знакам, обычно используемым в физике, тогда как для инженерного соглашения необходимо перевернуть все мнимые величины.

Комплексная диэлектрическая проницаемость обычно является сложной функцией частоты. ω, поскольку это наложенное описание разброс явления, происходящие на нескольких частотах. Диэлектрическая функция ε(ω) должен иметь полюсы только для частот с положительными мнимыми частями и, следовательно, удовлетворяет Отношения Крамерса – Кронига. Однако в узких частотных диапазонах, которые часто изучаются на практике, диэлектрическая проницаемость может быть аппроксимирована частотно-независимой или модельными функциями.

На данной частоте мнимая часть, ε″, приводит к потере поглощения, если он положительный (в приведенном выше соглашении о знаках), и к выигрышу, если он отрицательный. В более общем плане мнимые части собственные значения тензора анизотропной диэлектрической проницаемости.

В случае твердых тел сложная диэлектрическая функция тесно связана с зонной структурой. Первичная величина, которая характеризует электронную структуру любого кристаллического материала, - это вероятность фотон поглощение, которое напрямую связано с мнимой частью оптической диэлектрической проницаемости ε(ω). Оптическая диэлектрическая функция определяется фундаментальным выражением:^[10]

${ displaystyle varepsilon ( omega) = 1 + { frac {8 pi ^ {2} e ^ {2}} {m ^ {2}}} sum _ {c, v} int W_ {c , v} (E) { bigl (} varphi ( hbar omega -E) - varphi ( hbar omega + E) { bigr)} , dx.}$

В этом выражении W_c,v(E) представляет собой продукт Зона Бриллюэна -средняя вероятность перехода при энергии E с совместным плотность состояний,^[11][12] J_c,v(E); φ - функция уширения, представляющая роль рассеяния в размытии энергетических уровней.^[13] В целом уширение промежуточное между Лоренциан и Гауссовский;^[14][15] для сплава он несколько ближе к гауссову из-за сильного рассеяния на статистических флуктуациях локального состава в нанометровом масштабе.

Тензорная диэлектрическая проницаемость

Согласно Модель Друде намагниченной плазмы, более общее выражение, которое учитывает взаимодействие носителей с переменным электрическим полем миллиметрового и микроволнового диапазона в аксиально намагниченном полупроводнике, требует выражения диэлектрической проницаемости в виде недиагонального тензора.^[16] (смотрите также Электро-вращение ).

${ displaystyle mathbf {D} ( omega) = { begin {vmatrix} varepsilon _ {1} & - i varepsilon _ {2} & 0 i varepsilon _ {2} & varepsilon _ {1 } & 0 0 & 0 & varepsilon _ {z} конец {vmatrix}} operatorname { mathbf {E}} ( omega)}$

Если ε₂ обращается в нуль, то тензор диагонален, но не пропорционален тождеству, и среда называется одноосной средой, которая имеет свойства, аналогичные свойствам одноосный кристалл.

Классификация материалов

Материалы можно классифицировать по их комплексной диэлектрической проницаемости. ε, при сравнении его реальных ε′ и воображаемый ε″ компоненты (или, что то же самое, проводимость, σ, с учетом последнего). А идеальный дирижер имеет бесконечную проводимость, σ = ∞, а идеальный диэлектрик это материал, который вообще не имеет проводимости, σ = 0; этот последний случай действительной диэлектрической проницаемости (или комплексной диэлектрической проницаемости с нулевой мнимой составляющей) также связан с названием медиа без потерь.^[17] Обычно, когда σ/ωε′ ≪ 1 мы рассматриваем материал как диэлектрик с низкими потерями (хотя и не совсем без потерь), тогда как σ/ωε′ ≫ 1 связан с хороший дирижер; такие материалы с хорошей проводимостью дают большое количество потеря которые препятствуют распространению электромагнитных волн, поэтому также называются медиа с потерями. Материалы, не подпадающие под эти ограничения, считаются общедоступными.

Потерянная среда

В случае среды с потерями, т.е. когда ток проводимости не является незначительным, общая плотность протекающего тока составляет:

${ displaystyle J _ { text {tot}} = J _ { mathrm {c}} + J _ { mathrm {d}} = sigma E + i omega varepsilon 'E = i omega { hat { варепсилон}} E}$

где

• σ это проводимость среды;
• ${ displaystyle varepsilon '= varepsilon _ {0} varepsilon _ {r}}$ - действительная часть диэлектрической проницаемости.
• ${ displaystyle { hat { varepsilon}} = varepsilon '-i varepsilon' '}$комплексная диэлектрическая проницаемость

Размер ток смещения зависит от частота ω приложенного поля E; в постоянном поле нет тока смещения.

В этом формализме комплексная диэлектрическая проницаемость определяется как:^[18][19]

${ displaystyle { hat { varepsilon}} = varepsilon ' left (1-я { frac { sigma} { omega varepsilon'}} right) = varepsilon '-i { frac { сигма} { omega}}}$

В общем, поглощение электромагнитной энергии диэлектриками покрывается несколькими различными механизмами, которые влияют на форму диэлектрической проницаемости в зависимости от частоты:

• Во-первых, это расслабление эффекты, связанные с постоянными и индуцированными молекулярные диполи. На низких частотах поле изменяется достаточно медленно, чтобы диполи могли достигать равновесие прежде, чем поле заметно изменится. Для частот, на которых ориентация диполя не может следовать за приложенным полем из-за вязкость среды, поглощение энергии поля приводит к диссипации энергии. Механизм релаксации диполей называется диэлектрическая релаксация а для идеальных диполей описывается классическим Дебай релаксация.
• Во-вторых, резонансные эффекты, возникающие из-за вращения или колебаний атомов, ионы, или электроны. Эти процессы наблюдаются в окрестности их характерных частоты поглощения.

Вышеупомянутые эффекты часто объединяются, чтобы вызвать нелинейные эффекты в конденсаторах. Например, диэлектрическое поглощение относится к неспособности конденсатора, который был заряжен в течение длительного времени, полностью разрядиться при кратковременном разряде. Хотя идеальный конденсатор будет оставаться при нулевом напряжении после разряда, реальные конденсаторы будут развивать небольшое напряжение, явление, которое также называют пропитка или действие батареи. Для некоторых диэлектриков, таких как многие полимерные пленки, результирующее напряжение может быть менее 1-2% от исходного напряжения. Однако он может достигать 15–25% в случае электролитические конденсаторы или суперконденсаторы.

Квантово-механическая интерпретация

С точки зрения квантовая механика, диэлектрическая проницаемость объясняется атомный и молекулярный взаимодействия.

На низких частотах молекулы в полярных диэлектриках поляризованы приложенным электрическим полем, которое вызывает периодические вращения. Например, на микроволновая печь частоты, микроволновое поле вызывает периодическое вращение молекул воды, достаточное для разрушения водородные связи. Поле действует против связей, и энергия поглощается материалом в виде высокая температура. Вот почему микроволновые печи очень хорошо подходят для материалов, содержащих воду. Есть два максимума мнимой составляющей (показателя поглощения) воды, один на частоте микроволн, а другой на частоте далекого ультрафиолета (УФ). Оба этих резонанса находятся на более высоких частотах, чем рабочая частота микроволновых печей.

На умеренных частотах энергия слишком высока, чтобы вызвать вращение, но слишком низка, чтобы напрямую влиять на электроны, и поглощается в виде резонансных молекулярных колебаний. В воде именно здесь показатель поглощения начинает резко падать, а минимум мнимой диэлектрической проницаемости приходится на частоту синего света (оптический режим).

На высоких частотах (таких как УФ и выше) молекулы не могут расслабиться, и энергия полностью поглощается атомами, возбуждая электрон уровни энергии. Таким образом, эти частоты классифицируются как ионизирующее излучение.

При проведении полного ab initio (то есть моделирование из первых принципов) теперь возможно с помощью вычислений, оно еще не получило широкого распространения. Таким образом, феноменологическая модель считается адекватным методом фиксации экспериментального поведения. В Модель Дебая и Модель Лоренца используйте линейное представление с сосредоточенными параметрами системы первого и второго порядка (соответственно, например, RC и LRC резонансный контур).

Измерение

Относительную диэлектрическую проницаемость материала можно определить с помощью различных статических электрических измерений. Комплексная диэлектрическая проницаемость оценивается в широком диапазоне частот с использованием различных вариантов диэлектрическая спектроскопия, охватывающий почти 21 порядок из 10⁻⁶ до 10¹⁵ герц. Кроме того, используя криостаты и духовки, диэлектрические свойства среды можно охарактеризовать по множеству температур. Для изучения систем для таких разнообразных полей возбуждения используется ряд измерительных установок, каждая из которых соответствует определенному диапазону частот.

Различные методы микроволновых измерений описаны в Chen. и другие..^[20] Типичные ошибки для Метод Хакки-Коулмана использование шайбы материала между проводящими плоскостями составляет около 0,3%.^[21]

• Низкая частота область времени измерения (10⁻⁶ до 10³ Гц)
• Низкая частота частотная область измерения (10⁻⁵ до 10⁶ Гц)
• Отражательные коаксиальные методы (10⁶ до 10¹⁰ Гц)
• Коаксиальный метод передачи (10⁸ до 10¹¹ Гц)
• Квазиоптический методы (10⁹ до 10¹⁰ Гц)
• Терагерцовая спектроскопия во временной области (10¹¹ до 10¹³ Гц)
• Методы преобразования Фурье (10¹¹ до 10¹⁵ Гц)

На инфракрасных и оптических частотах распространенным методом является эллипсометрия. Двойная поляризационная интерферометрия также используется для измерения комплексного показателя преломления очень тонких пленок на оптических частотах.

Смотрите также

• Акустическое затухание
• Функциональная теория плотности
• Экранирование электрического поля
• Отношения Грина – Кубо
• Функция Грина (теория многих тел)
• Функция линейного отклика
• Вращательное броуновское движение
• Электромагнитная проницаемость

Заметки

использованная литература

дальнейшее чтение

• К. Дж. Ф. Ботчер, О. К. фон Белль и Пауль Бордевик (1973) Теория электрической поляризации: диэлектрическая поляризация, том 1, (1978) том 2, Elsevier ISBN  0-444-41579-3.
• Артур Р. фон Хиппель (1954) Диэлектрики и волны ISBN  0-89006-803-8
• Редактор Артура фон Хиппеля (1966) Диэлектрические материалы и приложения: статьи 22 авторов ISBN  0-89006-805-4.

внешние ссылки

• Электромагнетизм, глава из онлайн-учебника
• Что это за штука с застрявшим зарядом. . ., Другой подход к некоторым проблемам с конденсаторами
• Комплексная диэлектрическая проницаемость и показатель преломления металлов
• DrudeLorentz.com Онлайн-база данных по построению и параметризации моделей диэлектрической проницаемости Друде-Лоренца для обычных металлов