Зона Бриллюэна - Brillouin zone

Обратные решетки (точки) и соответствующие им первые зоны Бриллюэна (а) квадратная решетка и (б) шестиугольная решетка.

В математика и физика твердого тела, первый Зона Бриллюэна однозначно определенная примитивная клетка в взаимное пространство. Таким же образом Решетка Браве делится на Клетки Вигнера – Зейтца в реальной решетке обратная решетка разбивается на зоны Бриллюэна. Границы этой ячейки задаются плоскостями, относящимися к точкам на обратная решетка. Важность зоны Бриллюэна проистекает из описания волн в периодической среде, которое дает Теорема Блоха, в котором обнаружено, что решения могут быть полностью охарактеризованы их поведением в единственной зоне Бриллюэна.

Первая зона Бриллюэна - это локус точек в обратном пространстве, которые ближе к началу обратной решетки, чем к любым другим точкам обратной решетки (см. вывод ячейки Вигнера – Зейтца). Другое определение - это набор точек в k-пространство, в которое можно попасть из исходной точки без пересечения Самолет Брэгга. Эквивалентно, это Ячейка Вороного вокруг начала обратной решетки.

k-векторы, выходящие за пределы первой зоны Бриллюэна (красный цвет), не несут больше информации, чем их аналоги (черные) в первой зоне Бриллюэна. k на краю зоны Бриллюэна - пространственная Частота Найквиста волн в решетке, потому что это соответствует половине длины волны, равной межатомному интервалу решетки а.[1] Смотрите также Псевдонимы § Выборочные синусоидальные функции для получения дополнительной информации об эквивалентности k-векторов.
Зона Бриллюэна (фиолетовая) и неприводимая зона Бриллюэна (красная) для шестиугольная решетка.

Есть еще второй, третий, и Т. Д., Зоны Бриллюэна, соответствующие последовательности непересекающихся областей (все с одинаковым объемом) на увеличивающихся расстояниях от начала координат, но они используются реже. В результате первый Зону Бриллюэна часто называют просто Зона Бриллюэна. В целом п-я зона Бриллюэна состоит из множества точек, которые могут быть достигнуты из начала координат точным пересечением п - 1 отличный самолет Брэгга. Связанная концепция - это концепция неприводимая зона Бриллюэна, которая является первой зоной Бриллюэна, приведенной ко всем симметриям точечная группа решетки (точечная группа кристалла).

Концепция зоны Бриллюэна была разработана Леон Бриллюэн (1889–1969), французский физик.[2]

Критические точки

Первая зона Бриллюэна Решетка FCC, а усеченный октаэдр, показывая метки симметрии для линий и точек с высокой симметрией

Особый интерес представляют несколько точек высокой симметрии - они называются критическими точками.[3]

СимволОписание
ΓЦентр зоны Бриллюэна
Простой куб
MЦентр края
рУгловая точка
ИксЦентр лица
Гранецентрированная кубическая
KСередина ребра, соединяющего две шестиугольные грани
LЦентр шестиугольной грани
UСередина ребра, соединяющего шестиугольник и квадратную грань
WУгловая точка
ИксЦентр квадратного лица
Телоцентрированный кубический
ЧАСУгловая точка, соединяющая четыре края
NЦентр лица
пУгловая точка, соединяющая три края
Шестиугольный
АЦентр шестиугольной грани
ЧАСУгловая точка
KСередина кромки, соединяющей две прямоугольные грани
LСередина ребра, соединяющего шестиугольную и прямоугольную грань
MЦентр прямоугольного лица

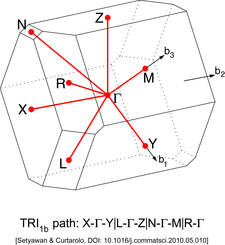
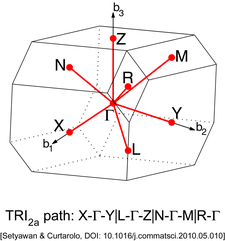
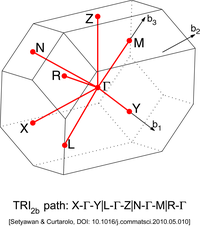
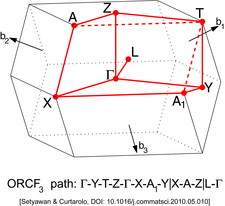
Другие решетки имеют другие типы точек высокой симметрии. Их можно найти на иллюстрациях ниже.

Типы зон Бриллюэна[4]
Решетчатая системаРешетка Браве

(Сокращение)

ТриклиникПримитивная триклиника

(TRI)

Триклинная решетка типа 1a (TRI1a)

Триклинная решетка типа 1a (зона Бриллюэна) .png

Триклинная решетка типа 1b (TRI1b)

Триклинная решетка типа 1b (зона Бриллюэна) .png

Триклинная решетка типа 2a (TRI2a)

Триклинная решетка типа 2a (зона Бриллюэна) .png

Триклинная решетка типа 2b (TRI2b)

Триклинная решетка типа 2b (зона Бриллюэна) .png

МоноклиникаПримитивная моноклиника

(MCL)

Моноклиническая решетка (MCL)

MCL.png

Базоцентрированная моноклиника

(MCLC)

Базоцентрированная моноклинная решетка типа 1 (MCLC1)

MCLC1.png

Базовая центрированная моноклинная решетка типа 2 (MCLC2)

Базоцентрированная моноклинная решетка типа 2 (зона Бриллюэна) .png

Базовая центрированная моноклинная решетка типа 3 (MCLC3)

MCLC3.png

Базовая центрированная моноклинная решетка типа 4 (MCLC4)

MCLC4.png

Базовая центрированная моноклинная решетка типа 5 (MCLC5)

MCLC5.png

ОрторомбическийПримитивный орторомбический

(ORC)

Простая орторомбическая решетка (ORC)

Простая орторомбическая решетка (зона Бриллюэна) .png

Орторомбическая с центром в основании

(ORCC)

Орторомбическая решетка с центром в основании (ORCC)

Орторомбическая решетка с центром в основании (зона Бриллюэна) .png

Телоцентрированный ромбический

(ORCI)

Телоцентрированная орторомбическая решетка (ORCI)

Телоцентрированная орторомбическая решетка (зона Бриллюэна) .png

Орторомбическая гранецентрированная

(ORCF)

Орторомбическая гранецентрированная решетка типа 1 (ORCF1)

Гранецентрированная орторомбическая решетка типа 1 (зона Бриллюэна) .png

Орторомбическая гранецентрированная решетка типа 2 (ORCF2)

Орторомбическая гранецентрированная решетка типа 2 (зона Бриллюэна) .png

Орторомбическая гранецентрированная решетка типа 3 (ORCF3)

Орторомбическая гранецентрированная решетка типа 3 (зона Бриллюэна) .png

ТетрагональныйПервобытный тетрагональный

(ТЕТ)

Простая тетрагональная решетка (TET)

Простая Тетрагональная Решетка (Зона Бриллюэна) .png

Тетрагональный центр тела

(BCT)

Телоцентрированная тетрагональная решетка типа 1 (BCT1)

Телоцентрированная тетрагональная решетка типа 1 (зона Бриллюэна) .png

Телоцентрированная тетрагональная решетка типа 2 (BCT2)

Телоцентрированная тетрагональная решетка типа 2 (зона Бриллюэна) .png

РомбоэдрическийПримитивный ромбэдерал

(БРЗ)

Ромбоэдрическая решетка типа 1 (RHL1)

RHL1.png

Ромбоэдрическая решетка типа 2 (RHL2)

RHL2.png

ШестиугольныйПримитивный шестиугольник

(HEX)

Шестиугольная решетка (HEX)

HEX.png

КубическийПримитивная кубическая

(КУБ)

Простая кубическая решетка (CUB)

Простая кубическая решетка (зона Бриллюэна) .png

Телоцентрированный кубический

(BCC)

Телоцентрированная кубическая решетка (ОЦК)

Телоцентрированная кубическая решетка (зона Бриллюэна) .png

Гранецентрированная кубическая

(FCC)

Гранецентрированная кубическая решетка (FCC)

Гранецентрированная кубическая решетка (зона Бриллюэна) .png

Смотрите также

Строительство зоны Бриллюэна выбранная область дифракции, используя электроны с энергией 300 кэВ.

Рекомендации

  1. ^ «Тема 5-2: Частота Найквиста и групповая скорость» (PDF). В двух словах о физике твердого тела. Колорадская горная школа.
  2. ^ Бриллюэн, Л. (1930). "Свободные электроны в металлах и роль отражений Брэгга" [Свободные электроны в металлах и роль брэгговских отражений]. Journal de Physique et le Radium (На французском). EDP ​​Sciences. 1 (11): 377–400. Дои:10.1051 / jphysrad: 01930001011037700. ISSN  0368-3842.
  3. ^ Ибах, Харальд; Лют, Ханс (1996). Физика твердого тела, введение в основы материаловедения (2-е изд.). Springer-Verlag. ISBN  978-3-540-58573-2.
  4. ^ Сетьяван, Вахю; Куртароло, Стефано (2010). «Расчет высокопроизводительной электронной зонной структуры: проблемы и инструменты». Вычислительное материаловедение. 49 (2): 299–312. arXiv:1004.2974. Bibcode:2010arXiv1004.2974S. Дои:10.1016 / j.commatsci.2010.05.010.

Библиография

внешняя ссылка