Примитивная ячейка - Primitive cell

В геометрия, биология, минералогия, и физика твердого тела, а примитивная клетка это ячейка соответствует единому точка решетки конструкции с дискретными поступательная симметрия. Это понятие используется, в частности, при описании Кристальная структура в двух и трех измерениях, хотя это имеет смысл во всех измерениях. Решетка может быть охарактеризована геометрией ее примитивной ячейки.

В некоторых случаях полная симметрия кристаллической структуры не очевидна из примитивной элементарной ячейки, и в этих случаях обычная ячейка может быть использовано. Обычная ячейка (которая может быть или не быть примитивной) представляет собой наименьшую элементарную ячейку, оси которой следуют за осями симметрии кристаллической структуры. Объем обычной ячейки всегда является целым кратным (обычно 1, 2, 3 или 4) объему элементарной ячейки.^[1]

Примитивная клетка - это первобытное место. Примитивная единица - это часть мозаики (обычно параллелограмм или набор соседних плиток), которая генерирует всю мозаику, используя только трансляции, и является настолько маленькой, насколько это возможно.

Примитивная клетка - это фундаментальная область только относительно трансляционной симметрии. В случае дополнительных симметрий фундаментальная область меньше.

Обзор

А кристалл можно классифицировать по его решетке и атомам, которые лежат в примитивной ячейке ( основа). Ячейка заполнит все пространство решетки, не оставляя зазоров, повторением операций трансляции кристалла.

По определению примитивная ячейка должна содержать ровно одну и только одну точку решетки. За элементарные ячейки как правило, точки решетки, общие для $п$ клетки считаются как 1/ $п$ узлов решетки, содержащихся в каждой из этих ячеек; так, например, примитивная элементарная ячейка в трех измерениях, которая имеет точки решетки только в восьми вершинах, считается содержащей 1/8 каждого из них.^[2] Альтернативная концептуализация заключается в последовательном выборе только одного из $п$ точки решетки принадлежат данной элементарной ячейке (так что другие $1-н$ точки решетки принадлежат соседним элементарным ячейкам).

Два измерения

В параллелограмм - общая примитивная ячейка для плоскости.

Двухмерная примитивная клетка - это параллелограмм, которые в особых случаях могут иметь ортогональные углы или равные длины, или и то, и другое.

	Обычные примитивные клетки			Оригинальный примитивные клетки

Имя формы	Параллелограмм	Прямоугольник	Квадрат	Ромб
Решетка Браве	Примитивная моноклиника	Примитивный орторомбический	Примитивный тетрагональный	Центрированный орторомбический

Три измерения

А параллелепипед является общей примитивной клеткой для трехмерного пространства.

В примитивные векторы перевода $а \to 1$ , $а \to 2$ , $а \to 3$ охватывают ячейку решетки наименьшего объема для конкретной трехмерной решетки и используются для определения вектора трансляции кристалла

{ displaystyle { vec {T}} = u_ {1} { vec {a}} _ {1} + u_ {2} { vec {a}} _ {2} + u_ {3} { vec {a}} _ {3},}

куда $ты 1$ , $ты 2$ , $ты 3$ - целые числа, сдвиг на которые оставляет решетку неизменной.^{[примечание 1]} То есть для точки решетки $р$ , расположение точек кажется таким же из $р' = р + Т \to$ как из $р$ .^[3]

Поскольку примитивная ячейка определяется примитивными осями (векторами) $а \to 1$ , $а \to 2$ , $а \to 3$ , громкость $V п$ примитивной ячейки задается параллелепипед от вышеуказанных осей как

{ displaystyle V _ { mathrm {p}} = left | { vec {a}} _ {1} cdot ({ vec {a}} _ {2} times { vec {a}} _ {3}) right |.}

Для любой трехмерной решетки можно найти примитивные ячейки, которые параллелепипеды, которые в особых случаях могут иметь ортогональные углы или равные длины, или и то, и другое. Хотя это и не требуется математически, по соглашению обычно определяют примитивную ячейку параллелепипеда так, чтобы на каждом углу была точка решетки. Когда точки решетки находятся в углу, каждая точка решетки используется совместно с восемью разными примитивными ячейками, поэтому каждая точка решетки будет вносить только 1/8 точки решетки в каждую из этих ячеек. Однако существует восемь углов, поэтому на каждую ячейку по-прежнему приходится одна точка решетки, как того требует определение. Некоторые из четырнадцати трехмерных Решетки Браве представлены с использованием таких примитивных ячеек параллелепипеда, как показано ниже.

Обычная примитивная ячейка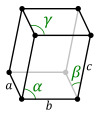
Имя формы	Параллелепипед	Косой прямоугольный призма	Прямоугольный кубовид	Квадрат кубовид	Тригональный трапецоэдр	Куб
Решетка Браве	Примитивный Триклиник	Примитивный Моноклиника	Примитивный Орторомбический	Примитивный Тетрагональный	Примитивный Ромбоэдрический	Примитивный Кубический

Другие решетки Бравэ также имеют примитивные ячейки в форме параллелепипеда, но для облегчения различения на основе симметрии они представлены обычными ячейками, которые содержат более одной точки решетки.

Примитивная ячейка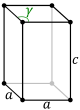
Имя формы	Косая ромбическая призма	Правый ромбический призма
Обычная ячейка
Решетка Браве	По центру основания Моноклиника	По центру основания Орторомбический

Ячейка Вигнера – Зейтца

В качестве альтернативы элементарной ячейке для каждой решетки Браве существует другой вид примитивной ячейки, называемый Ячейка Вигнера – Зейтца. В ячейке Вигнера – Зейтца точка решетки находится в центре ячейки, и для большинства решеток Бравэ форма не является параллелограммом или параллелепипедом. Это разновидность Ячейка Вороного. Ячейка Вигнера – Зейтца обратная решетка в импульсное пространство называется Зона Бриллюэна.

Смотрите также

Примечания

^ В $п$ размерность вектора трансляции кристалла будет
${ displaystyle { vec {T}} = sum _ {i = 1} ^ {n} u_ {i} { vec {a}} _ {i}, quad { mbox {where}} u_ { i} in mathbb {Z} quad forall i.}$
То есть для точки решетки $р$ , расположение точек кажется таким же из $р' = р + Т \to$ как из $р$ .